27.1 相似的图形 课件(共17张PPT)人教版九年级数学下册
文档属性
| 名称 | 27.1 相似的图形 课件(共17张PPT)人教版九年级数学下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 917.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-03 21:07:33 | ||
图片预览




文档简介
(共17张PPT)
教学目标
(1)理解并掌握图形相似的概念,会判断相似图形;
(2)了解比例线段的定义;
(3)掌握相似多边形的概念,会根据特征识别相似多边形,并利用性质进行相关的计算.
重点难点
重点:探索相似图形的基本特征,特别是相似多边形的判定与性质
难点:四条线段成比例
27.1 图形的相似
人教版数学九年级下册第二十七章《相似三角形》
形状和大小完全相同的两个图形,是全等图形.
情景导入
观察下面两组图形,对比它们的形状和大小,你有什么发现?
观察下面两组图形,对比它们的形状和大小,你有什么发现?
形状相同的两个图形,叫做相似图形.
情景导入
思考:全等图形和相似图形之间有什么联系?
概念辨析
课堂练习:完成课本p25思考及练习
思考:(1)你能举出几个平面图形相似的例子吗?
(2)相似的两个图形可以通过怎样的变化得到?
动手实践
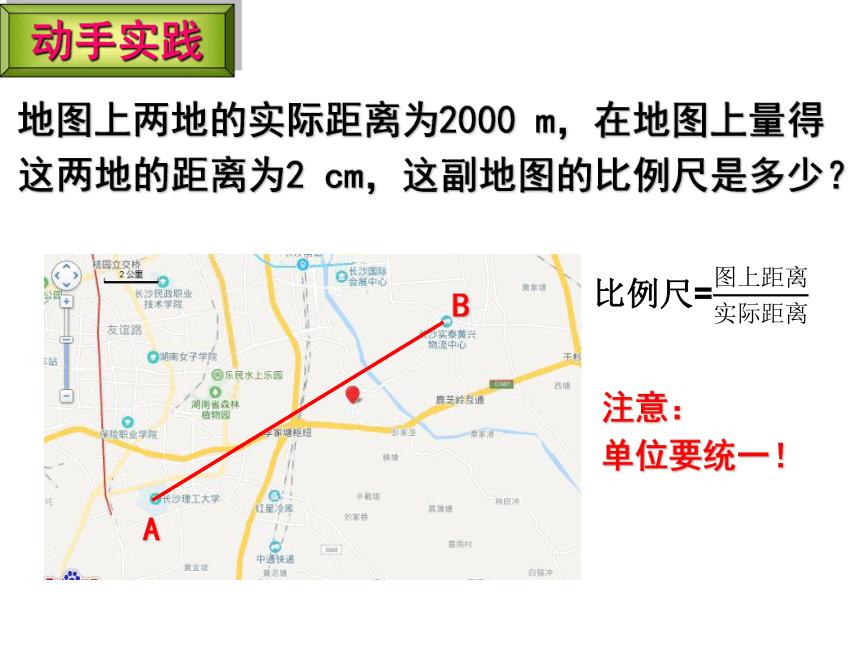
地图上两地的实际距离为2000 m,在地图上量得这两地的距离为2 cm,这副地图的比例尺是多少?
A
B
比例尺=
注意:
单位要统一!
动手实践
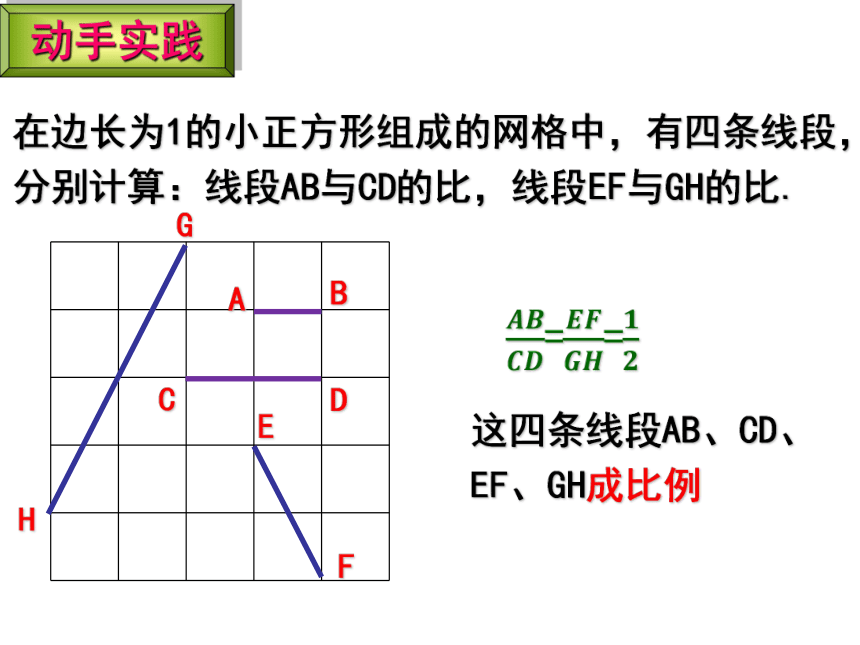
在边长为1的小正方形组成的网格中,有四条线段,分别计算:线段AB与CD的比,线段EF与GH的比.
A
B
==
C
D
H
G
E
F
这四条线段AB、CD、EF、GH成比例
概念生成
性质
即 线段a、b、c、d成比例 线段a、c、b、d成比例
对于四条线段a,b,c,d,如果其中两条线段的比与另两条线段的比相等,如 ,就说这四条线段成比例.
概念辨析
例1 下列各组长度的线段(单位:cm)中,成比例线段的是( )
A.2,3,4,5 B.1,3,4,10
C.1,3,4,6 D.1,3,4,12
D
练习1: 若线段a,b,c,d成比例,其中a=3cm,b=6cm,c=4cm,则d= cm.
8
已成比例,顺序确定,用等积式!
概念辨析
练习2:已知三条线段的长是1cm,cm,2cm,请你再添上一条线段,使这四条线段成比例线段,则这条线段长为 cm.
顺序不定,
需要讨论!
动脑思考
分别观察下面两组多边形,它们是相似图形吗?
要如何判断两个多边形的形状相同呢?
边数相同,且角分别相等,边成比例的两个多边形是相似的.
两个边数相同的多边形,如果它们的角分别相等,边成比例,那么这两个多边形叫做相似多边形. 相似多边形对应边的比叫相似比.
符号语言?以右图为例
注意:
定义既是判定,也是性质!
概念生成
A
B
C
D
A1
B1
C1
D1
相似多边形的定义如下:
例3 四边形ABCD与EFGH相似,求角α、β的度数,线段EH的长度x,以及相似比.
A
B
C
D
18cm
21cm
E
F
G
H
24cm
概念辨析
例2 两个大小不同的正方形相似吗?为什么?
课堂练习:完成课本p27最上面的第2,3题
课堂小结
今天你学到了什么?从知识和思想方法两个方面说明.
如图,在矩形ABCD中,EF∥AB,AB=3,BC=4,若矩形ABCD与矩形CFED相似,求BF的长.
E
F
D
C
B
A
拓展提升
A
B
C
D
如图,在矩形ABCD中,AB=4,AD=10,你能将它分割成两个小矩形,使它们成为相似图形吗?
A
B
C
D
4
10
E
F
A
B
C
D
F
E
A
B
C
D
F
E
4
8
2
4
拓展提升
例题1、下图是两个等边三角形,它们的角与边分别有什么关系?它们相似吗?
B
C
A
B
′
C
A
′
′
∠A= ∠A′
∠B= ∠B′
∠C= ∠C′
∵
∴ △ABC∽△ A′B′C′
判定
性质
典例分析
教学目标
(1)理解并掌握图形相似的概念,会判断相似图形;
(2)了解比例线段的定义;
(3)掌握相似多边形的概念,会根据特征识别相似多边形,并利用性质进行相关的计算.
重点难点
重点:探索相似图形的基本特征,特别是相似多边形的判定与性质
难点:四条线段成比例
27.1 图形的相似
人教版数学九年级下册第二十七章《相似三角形》
形状和大小完全相同的两个图形,是全等图形.
情景导入
观察下面两组图形,对比它们的形状和大小,你有什么发现?
观察下面两组图形,对比它们的形状和大小,你有什么发现?
形状相同的两个图形,叫做相似图形.
情景导入
思考:全等图形和相似图形之间有什么联系?
概念辨析
课堂练习:完成课本p25思考及练习
思考:(1)你能举出几个平面图形相似的例子吗?
(2)相似的两个图形可以通过怎样的变化得到?
动手实践
地图上两地的实际距离为2000 m,在地图上量得这两地的距离为2 cm,这副地图的比例尺是多少?
A
B
比例尺=
注意:
单位要统一!
动手实践
在边长为1的小正方形组成的网格中,有四条线段,分别计算:线段AB与CD的比,线段EF与GH的比.
A
B
==
C
D
H
G
E
F
这四条线段AB、CD、EF、GH成比例
概念生成
性质
即 线段a、b、c、d成比例 线段a、c、b、d成比例
对于四条线段a,b,c,d,如果其中两条线段的比与另两条线段的比相等,如 ,就说这四条线段成比例.
概念辨析
例1 下列各组长度的线段(单位:cm)中,成比例线段的是( )
A.2,3,4,5 B.1,3,4,10
C.1,3,4,6 D.1,3,4,12
D
练习1: 若线段a,b,c,d成比例,其中a=3cm,b=6cm,c=4cm,则d= cm.
8
已成比例,顺序确定,用等积式!
概念辨析
练习2:已知三条线段的长是1cm,cm,2cm,请你再添上一条线段,使这四条线段成比例线段,则这条线段长为 cm.
顺序不定,
需要讨论!
动脑思考
分别观察下面两组多边形,它们是相似图形吗?
要如何判断两个多边形的形状相同呢?
边数相同,且角分别相等,边成比例的两个多边形是相似的.
两个边数相同的多边形,如果它们的角分别相等,边成比例,那么这两个多边形叫做相似多边形. 相似多边形对应边的比叫相似比.
符号语言?以右图为例
注意:
定义既是判定,也是性质!
概念生成
A
B
C
D
A1
B1
C1
D1
相似多边形的定义如下:
例3 四边形ABCD与EFGH相似,求角α、β的度数,线段EH的长度x,以及相似比.
A
B
C
D
18cm
21cm
E
F
G
H
24cm
概念辨析
例2 两个大小不同的正方形相似吗?为什么?
课堂练习:完成课本p27最上面的第2,3题
课堂小结
今天你学到了什么?从知识和思想方法两个方面说明.
如图,在矩形ABCD中,EF∥AB,AB=3,BC=4,若矩形ABCD与矩形CFED相似,求BF的长.
E
F
D
C
B
A
拓展提升
A
B
C
D
如图,在矩形ABCD中,AB=4,AD=10,你能将它分割成两个小矩形,使它们成为相似图形吗?
A
B
C
D
4
10
E
F
A
B
C
D
F
E
A
B
C
D
F
E
4
8
2
4
拓展提升
例题1、下图是两个等边三角形,它们的角与边分别有什么关系?它们相似吗?
B
C
A
B
′
C
A
′
′
∠A= ∠A′
∠B= ∠B′
∠C= ∠C′
∵
∴ △ABC∽△ A′B′C′
判定
性质
典例分析
