28.1 锐角三角函数 课件(共30张PPT)人教版数学九年级下册
文档属性
| 名称 | 28.1 锐角三角函数 课件(共30张PPT)人教版数学九年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 649.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-03 21:08:24 | ||
图片预览



文档简介
(共30张PPT)
教学目标
(1)通过探究使学生知道:在直角三角形中,当锐角的度数一定时,无论这个直角三角形的大小如何,这个锐角的对边与斜边的比是一个固定值;
(2)能够根据边长计算锐角的正弦值或根据正弦值计算边长.
重点难点
重点:理解认识正弦概念,并利用概念计算正弦值.
难点:引导学生比较、分析并得出:直角三角形中,当锐角一定时,它的对边和斜边的比是一个固定值.
锐角三角函数
人教版数学九年级下册第二十八章《锐角三角函数》
美国人体工程学研究人员卡特·克雷加文调查发现,70%以上的女性喜欢穿鞋跟高度为6至7厘米左右的高跟鞋。但专家认为穿6厘米以上的高跟鞋,腿肚、背部等处的肌肉非常容易疲劳.
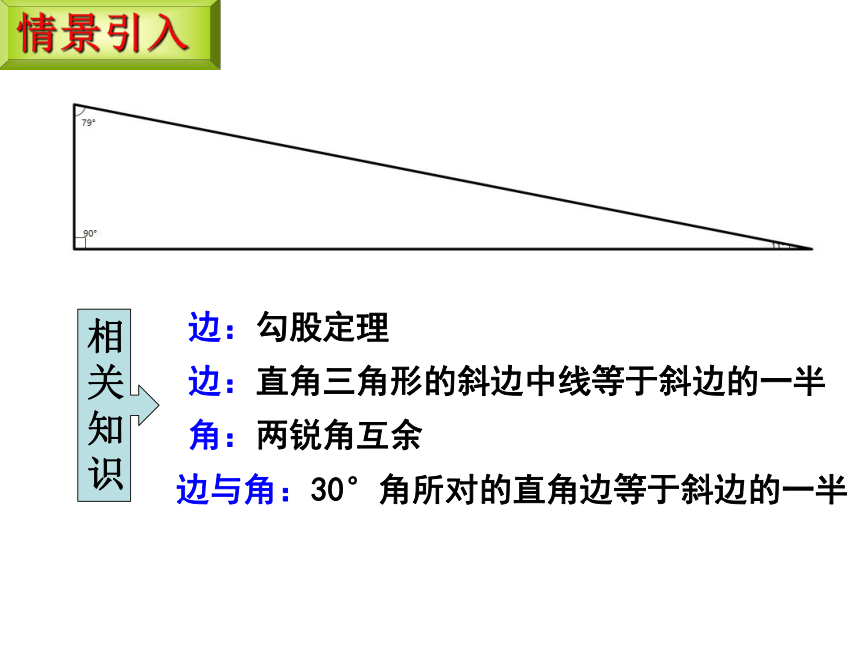
情景引入
鞋跟多高合适?
据研究,当高跟鞋的鞋底与地面的夹角为11度左右时,人脚的感觉最舒适。假设某成年人脚前掌到脚后跟长为15厘米,不难算出鞋跟在3厘米左右高度为最佳.
情景引入
边:勾股定理
相关知识
边:直角三角形的斜边中线等于斜边的一半
角:两锐角互余
边与角:30°角所对的直角边等于斜边的一半
A
B
C
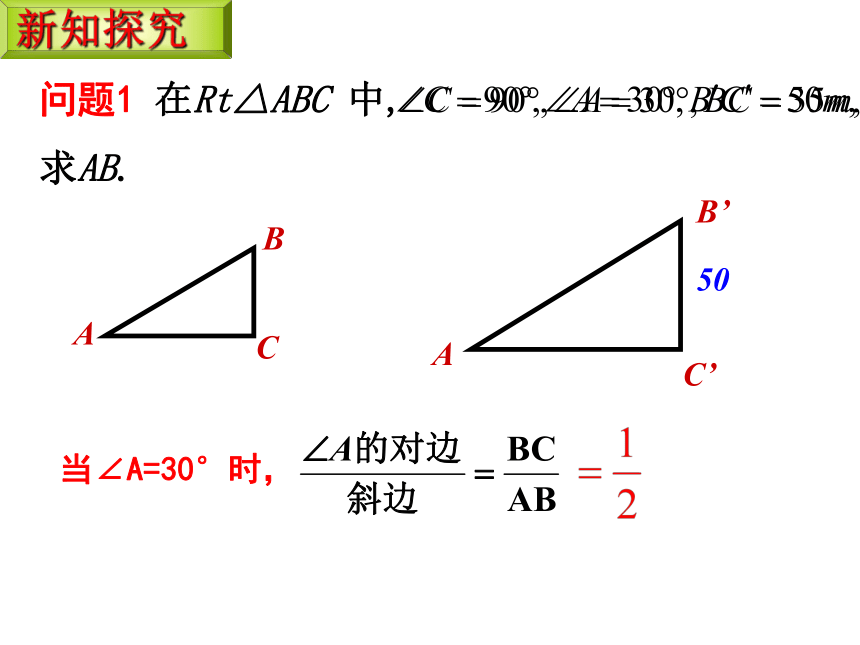
问题1 在Rt△ABC 中,
求AB.
A
B’
C’
50
当∠A=30°时,
新知探究
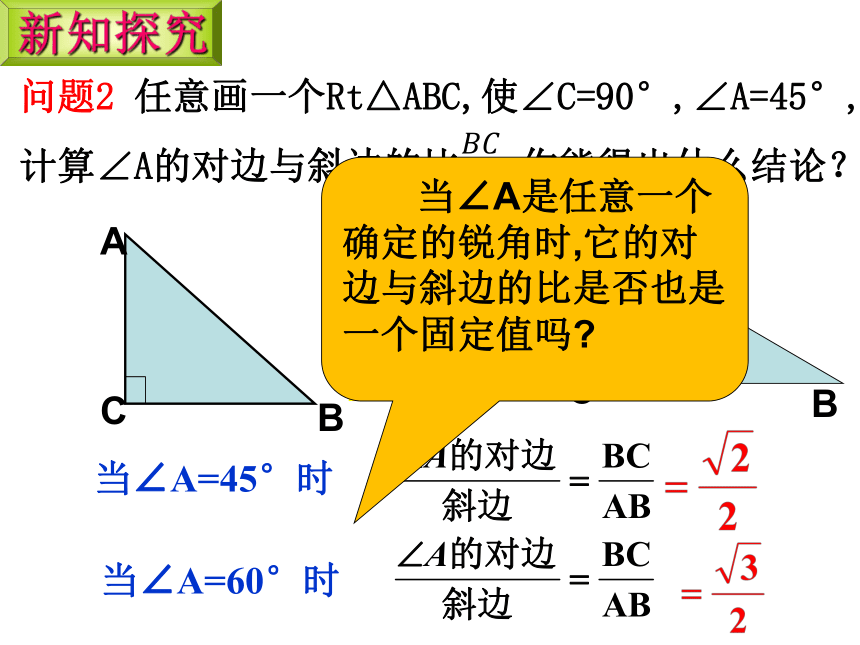
当∠A=45°时
问题2 任意画一个Rt△ABC,使∠C=90°,∠A=45°,计算∠A的对边与斜边的比,你能得出什么结论?
A
B
C
A
C
B
当∠A=60°时
当∠A是任意一个确定的锐角时,它的对边与斜边的比是否也是一个固定值吗
新知探究
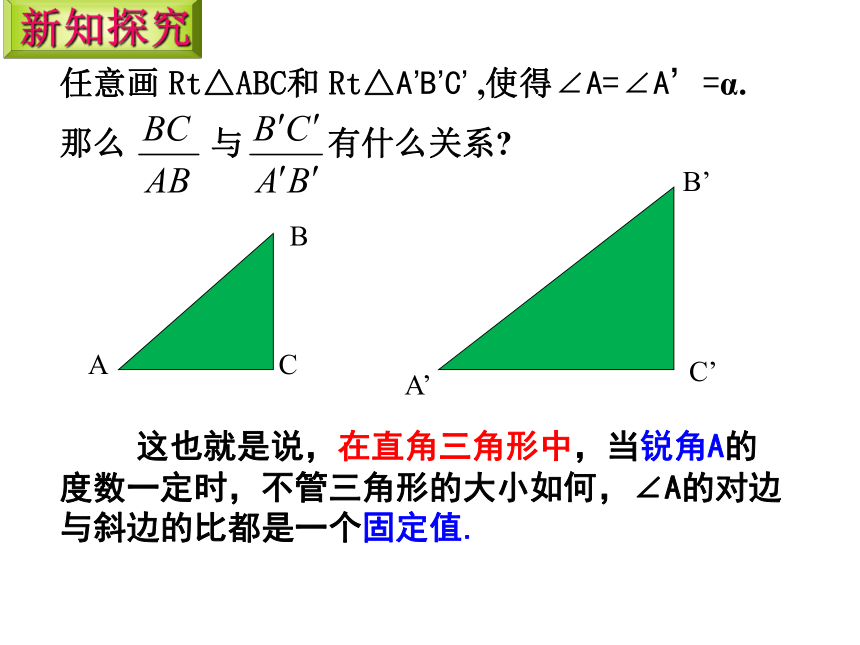
任意画 Rt△ABC和 Rt△A’B’C’ ,使得∠A=∠A’=α.
那么 与 有什么关系
A
C
B
A’
B’
C’
这也就是说,在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的对边与斜边的比都是一个固定值.
新知探究
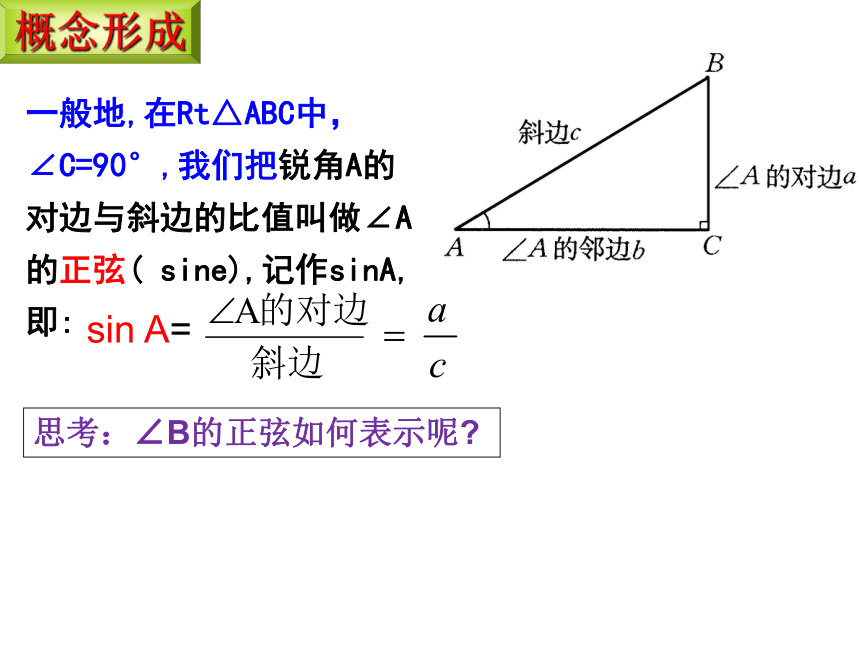
一般地,在Rt△ABC中,∠C=90°,我们把锐角A的对边与斜边的比值叫做∠A的正弦( sine),记作sinA,即:
sin A=
思考:∠B的正弦如何表示呢
概念形成
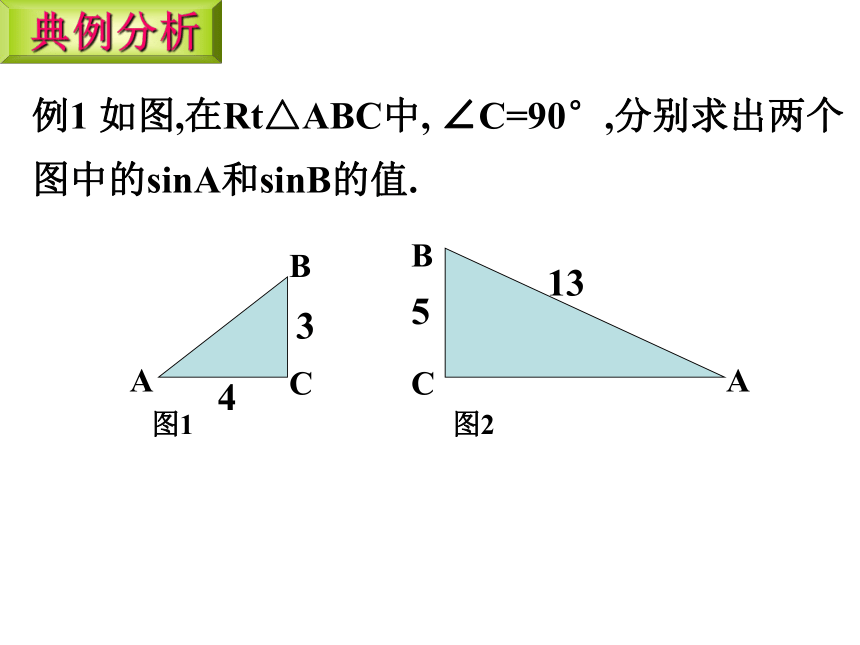
例1 如图,在Rt△ABC中, ∠C=90°,分别求出两个图中的sinA和sinB的值.
典例分析
A
C
B
A
C
B
3
4
13
5
图1
图2
(2)Rt△ABC中,∠C=90°,sinA= ,
则 BC = 4,AB= 5 .( )
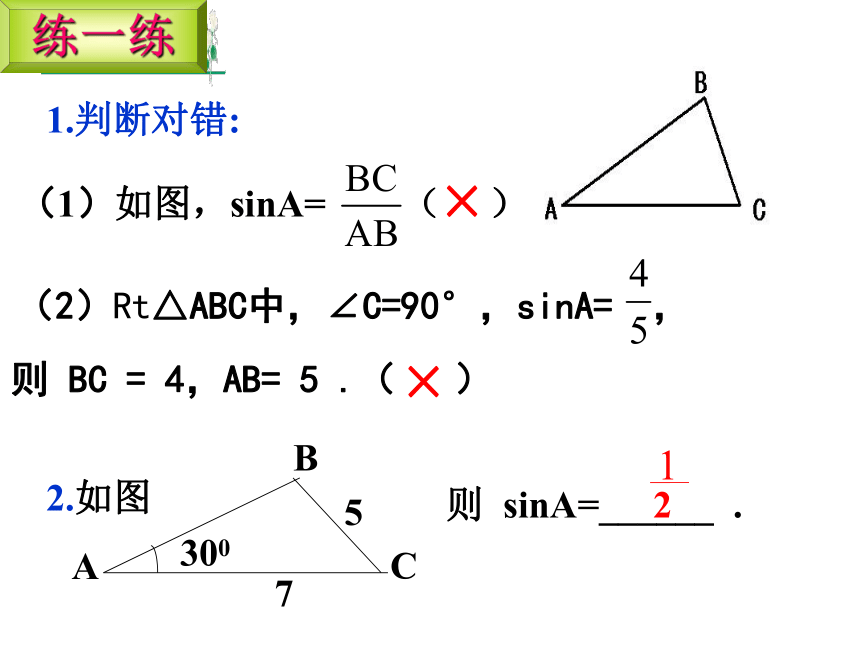
1.判断对错:
(1)如图,sinA= ( )
×
×
练一练
2.如图
A
C
B
5
7
300
则 sinA=______ .
1
2
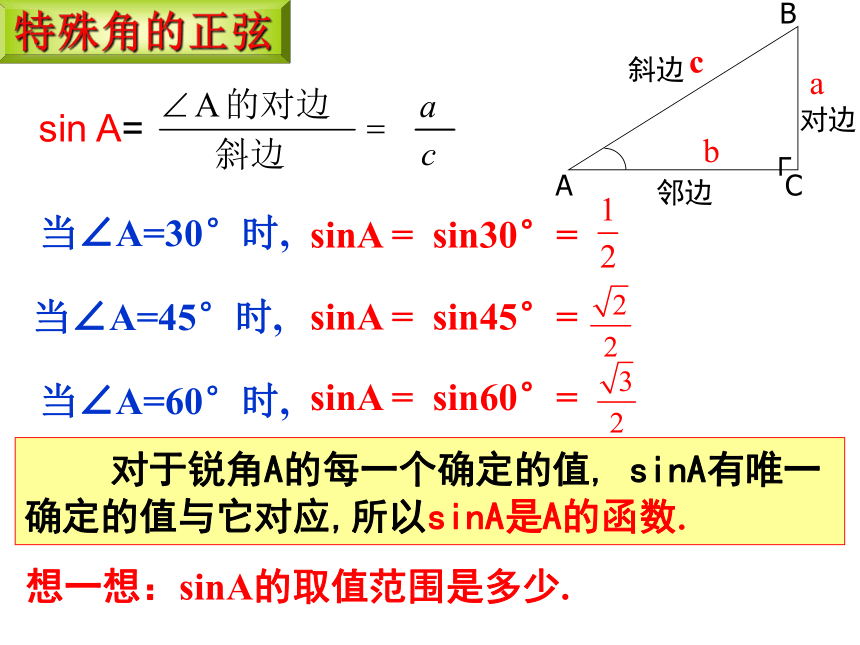
对于锐角A的每一个确定的值, sinA有唯一确定的值与它对应,所以sinA是A的函数.
当∠A=30°时,
A
B
C
对边
邻边
┌
斜边
a
b
c
sinA = sin30°=
当∠A=45°时,
sinA = sin45°=
sin A=
当∠A=60°时,
sinA = sin60°=
想一想:sinA的取值范围是多少.
特殊角的正弦
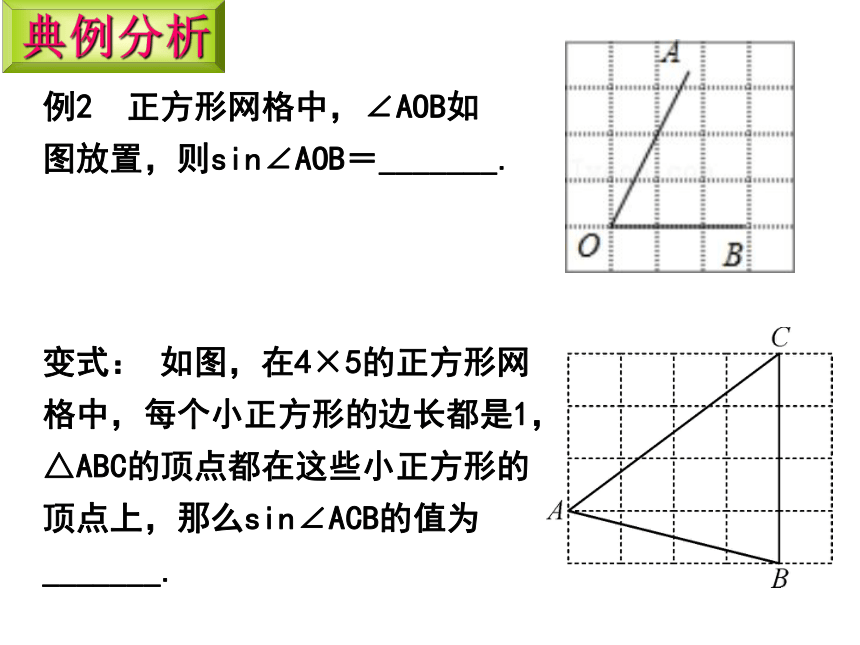
例2 正方形网格中,∠AOB如图放置,则sin∠AOB=_______.
典例分析
变式: 如图,在4×5的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在这些小正方形的顶点上,那么sin∠ACB的值为_______.
练习1 已知△ABC中,∠ACB=90°,CD⊥AB相交于D,若AB=5,BC=4,求sinα的值.
B
A
C
D
α
sinα=
你还有其他方法吗?
变式练习
例3 如图,在△ABC中,∠C=90°sinA= ,
BC=2, 求AB、AC的长.
典例分析
AC=3, 求AB、BC的长.
变式:如图,在△ABC中, AB=5,AC=6,sinA= ,求△ABC 的面积.
D
变式练习
1.锐角三角函数定义:
2.sinA是∠A的函数.
A
B
C
∠A的对边
┌
斜边
斜边
∠A的对边
sinA=
Sin300 =
sin45°=
sin60°=
小结
练习2 如图,已知△ABC的外接圆O的半径为3,AC=4,则sinB= .
变式练习
请大家尝试求一下sin15°的值。
A
C
B
D
15°
30°
15°
1
2
2
sin75°呢?
提高练习
如图,在Rt△ABC中,∠C=90°
A
C
B
对边a
邻边b
斜边c
当∠A确定时,∠A的对边与斜边的比就确定,此时,还有其他哪些边的比也是确定的?
思考探究1
如图,在Rt△ABC中,∠C=90°
A
C
B
对边a
邻边b
斜边c
概念定义
余弦
正切
正弦
锐角A的三角函数
例1 在Rt△ABC中,∠C=90°,AC=24,BC=7,求两个锐角的余弦值和正切值.
A
C
B
24
7
典例分析
解:在Rt△ABC中
25
练习1、如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,则cos∠B= .
A
C
B
4
3
快速练习
练习2、直角三角形的斜边和一条直角边的
比为13∶12,则其中最小的角的正切值为 .
练习3、已知锐角α的顶点在原点,一边在x轴的正半轴上,另一边在第一象限,其上一点P的坐标为(2,3),
则 tanα= ,cosα= .
x
o
y
P(2, 3)
α
快速练习
练习4、如图,以O为圆心的两个圆中,大圆的弦AB切小圆于点C,OA交小圆于点D,若小圆半径为2,大圆半径为4,则tan∠OAB= .
例2、如图,在Rt△ABC中,∠C=90°,,
A
C
B
3
AC=3,sinA = ,求cosA、tanB的值.
典例分析
类题练习
练习5、如图,在△ABC中,AB=AC=10,sinB= ,求BC.
练习6、如图,将∠AOB放在边长为1的小正方形组成的网格中,则cos∠AOB= .
拓展练习
练习7、如图,tan∠1 = .
练习8、如图,在Rt△ABC中,∠ACB=90°,AC=8,
BC=6,CD⊥AB,垂足为D,求tan∠BCD的值.
自我练习
课堂小结
余弦
正弦
如图,在Rt△ABC中,∠C=90°
A
C
B
对边a
邻边b
斜边c
正切
类题练习
如图,已知△ABC的三个顶点均在各点上,则cosA的值为 .
如图,在△ABC中,CD⊥AB,垂足为D,若AB=12,CD=6,tanA=1.5,求sinB+cosB的值.
解:
又 CD=6
类题练习
教学目标
(1)通过探究使学生知道:在直角三角形中,当锐角的度数一定时,无论这个直角三角形的大小如何,这个锐角的对边与斜边的比是一个固定值;
(2)能够根据边长计算锐角的正弦值或根据正弦值计算边长.
重点难点
重点:理解认识正弦概念,并利用概念计算正弦值.
难点:引导学生比较、分析并得出:直角三角形中,当锐角一定时,它的对边和斜边的比是一个固定值.
锐角三角函数
人教版数学九年级下册第二十八章《锐角三角函数》
美国人体工程学研究人员卡特·克雷加文调查发现,70%以上的女性喜欢穿鞋跟高度为6至7厘米左右的高跟鞋。但专家认为穿6厘米以上的高跟鞋,腿肚、背部等处的肌肉非常容易疲劳.
情景引入
鞋跟多高合适?
据研究,当高跟鞋的鞋底与地面的夹角为11度左右时,人脚的感觉最舒适。假设某成年人脚前掌到脚后跟长为15厘米,不难算出鞋跟在3厘米左右高度为最佳.
情景引入
边:勾股定理
相关知识
边:直角三角形的斜边中线等于斜边的一半
角:两锐角互余
边与角:30°角所对的直角边等于斜边的一半
A
B
C
问题1 在Rt△ABC 中,
求AB.
A
B’
C’
50
当∠A=30°时,
新知探究
当∠A=45°时
问题2 任意画一个Rt△ABC,使∠C=90°,∠A=45°,计算∠A的对边与斜边的比,你能得出什么结论?
A
B
C
A
C
B
当∠A=60°时
当∠A是任意一个确定的锐角时,它的对边与斜边的比是否也是一个固定值吗
新知探究
任意画 Rt△ABC和 Rt△A’B’C’ ,使得∠A=∠A’=α.
那么 与 有什么关系
A
C
B
A’
B’
C’
这也就是说,在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的对边与斜边的比都是一个固定值.
新知探究
一般地,在Rt△ABC中,∠C=90°,我们把锐角A的对边与斜边的比值叫做∠A的正弦( sine),记作sinA,即:
sin A=
思考:∠B的正弦如何表示呢
概念形成
例1 如图,在Rt△ABC中, ∠C=90°,分别求出两个图中的sinA和sinB的值.
典例分析
A
C
B
A
C
B
3
4
13
5
图1
图2
(2)Rt△ABC中,∠C=90°,sinA= ,
则 BC = 4,AB= 5 .( )
1.判断对错:
(1)如图,sinA= ( )
×
×
练一练
2.如图
A
C
B
5
7
300
则 sinA=______ .
1
2
对于锐角A的每一个确定的值, sinA有唯一确定的值与它对应,所以sinA是A的函数.
当∠A=30°时,
A
B
C
对边
邻边
┌
斜边
a
b
c
sinA = sin30°=
当∠A=45°时,
sinA = sin45°=
sin A=
当∠A=60°时,
sinA = sin60°=
想一想:sinA的取值范围是多少.
特殊角的正弦
例2 正方形网格中,∠AOB如图放置,则sin∠AOB=_______.
典例分析
变式: 如图,在4×5的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在这些小正方形的顶点上,那么sin∠ACB的值为_______.
练习1 已知△ABC中,∠ACB=90°,CD⊥AB相交于D,若AB=5,BC=4,求sinα的值.
B
A
C
D
α
sinα=
你还有其他方法吗?
变式练习
例3 如图,在△ABC中,∠C=90°sinA= ,
BC=2, 求AB、AC的长.
典例分析
AC=3, 求AB、BC的长.
变式:如图,在△ABC中, AB=5,AC=6,sinA= ,求△ABC 的面积.
D
变式练习
1.锐角三角函数定义:
2.sinA是∠A的函数.
A
B
C
∠A的对边
┌
斜边
斜边
∠A的对边
sinA=
Sin300 =
sin45°=
sin60°=
小结
练习2 如图,已知△ABC的外接圆O的半径为3,AC=4,则sinB= .
变式练习
请大家尝试求一下sin15°的值。
A
C
B
D
15°
30°
15°
1
2
2
sin75°呢?
提高练习
如图,在Rt△ABC中,∠C=90°
A
C
B
对边a
邻边b
斜边c
当∠A确定时,∠A的对边与斜边的比就确定,此时,还有其他哪些边的比也是确定的?
思考探究1
如图,在Rt△ABC中,∠C=90°
A
C
B
对边a
邻边b
斜边c
概念定义
余弦
正切
正弦
锐角A的三角函数
例1 在Rt△ABC中,∠C=90°,AC=24,BC=7,求两个锐角的余弦值和正切值.
A
C
B
24
7
典例分析
解:在Rt△ABC中
25
练习1、如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,则cos∠B= .
A
C
B
4
3
快速练习
练习2、直角三角形的斜边和一条直角边的
比为13∶12,则其中最小的角的正切值为 .
练习3、已知锐角α的顶点在原点,一边在x轴的正半轴上,另一边在第一象限,其上一点P的坐标为(2,3),
则 tanα= ,cosα= .
x
o
y
P(2, 3)
α
快速练习
练习4、如图,以O为圆心的两个圆中,大圆的弦AB切小圆于点C,OA交小圆于点D,若小圆半径为2,大圆半径为4,则tan∠OAB= .
例2、如图,在Rt△ABC中,∠C=90°,,
A
C
B
3
AC=3,sinA = ,求cosA、tanB的值.
典例分析
类题练习
练习5、如图,在△ABC中,AB=AC=10,sinB= ,求BC.
练习6、如图,将∠AOB放在边长为1的小正方形组成的网格中,则cos∠AOB= .
拓展练习
练习7、如图,tan∠1 = .
练习8、如图,在Rt△ABC中,∠ACB=90°,AC=8,
BC=6,CD⊥AB,垂足为D,求tan∠BCD的值.
自我练习
课堂小结
余弦
正弦
如图,在Rt△ABC中,∠C=90°
A
C
B
对边a
邻边b
斜边c
正切
类题练习
如图,已知△ABC的三个顶点均在各点上,则cosA的值为 .
如图,在△ABC中,CD⊥AB,垂足为D,若AB=12,CD=6,tanA=1.5,求sinB+cosB的值.
解:
又 CD=6
类题练习
