11.3.2 多边形的内角和 课件 (共18张PPT) 2023-2024学年人教版八年级数学上册
文档属性
| 名称 | 11.3.2 多边形的内角和 课件 (共18张PPT) 2023-2024学年人教版八年级数学上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 666.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-03 21:49:53 | ||
图片预览




文档简介
(共18张PPT)
人教版八年级数学上册
11.3.2 多边形的内角和
一、掌握多边形内角和公式。
二、能根据已知内角和求多边形边数和已知多边形边数求内角和。
三、理解多边形外角和。
学习目标
长风破浪会有时,直挂云帆济沧海
问题1:任意四边形的内角和是多少度呢?
问题2:你能利用三角形内角和的知识验证你的猜想吗?
360°
讲授新课
长风破浪会有时,直挂云帆济沧海
180 °×2 = 360°
A
B
C
D
A
B
D
C
B
D
A
B
D
C
B
D
A
B
D
C
B
D
提示:三角形是最简单的多边形,研究其它多边形可借助对角线将其分为若干个三角形
验一验
四边形的内角和等于360°
长风破浪会有时,直挂云帆济沧海
知识点1:多边形的内角和
合作探究
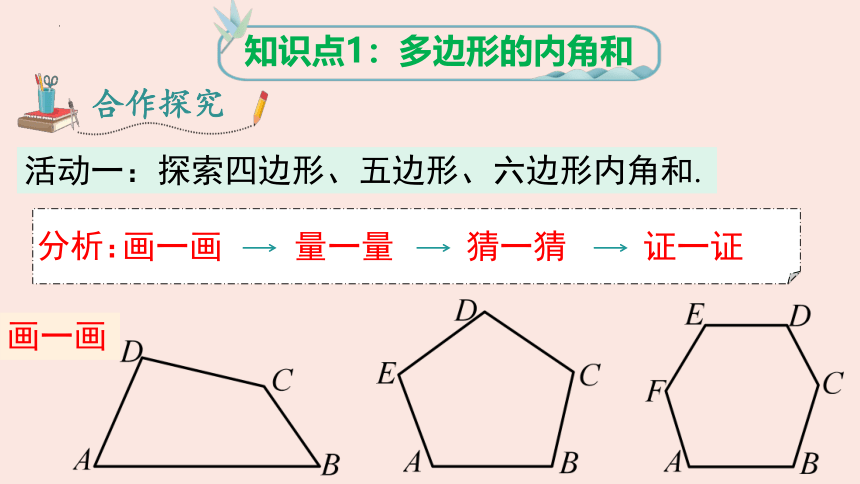
活动一:探索四边形、五边形、六边形内角和.
画一画
量一量
猜一猜
证一证
画一画
分析:
长风破浪会有时,直挂云帆济沧海
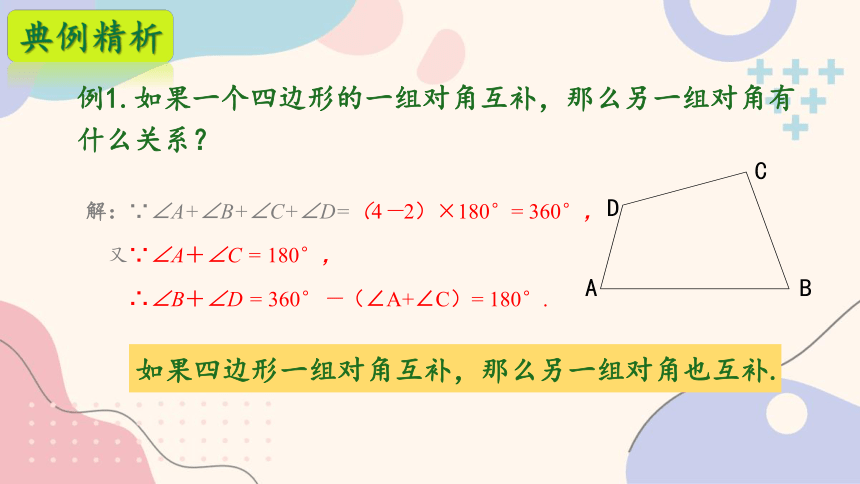
例1.如果一个四边形的一组对角互补,那么另一组对角有什么关系?
解:∵∠A+∠B+∠C+∠D=(4-2)×180°= 360°,
又∵∠A+∠C = 180°,
∴∠B+∠D = 360°-(∠A+∠C)= 180°.
如果四边形一组对角互补,那么另一组对角也互补.
A
C
D
B
典例精析
长风破浪会有时,直挂云帆济沧海
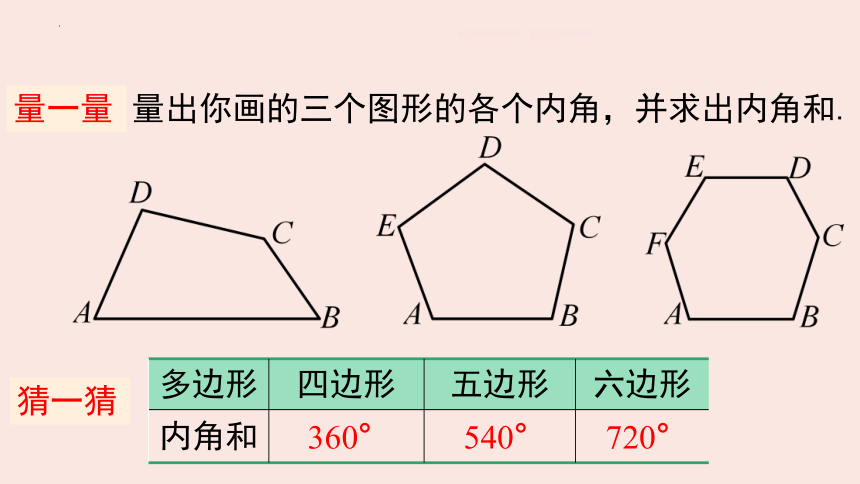
量出你画的三个图形的各个内角,并求出内角和.
多边形 四边形 五边形 六边形
内角和
量一量
猜一猜
360°
540°
720°
长风破浪会有时,直挂云帆济沧海
证一证
请用多种方法证明上述结论.
n 个三角形
多边形
未知
已知
以一个点为顶点连接对角线
连接内部一点与各顶点
连接边上任意一点与各顶点
分析:
长风破浪会有时,直挂云帆济沧海
如图,在四边形ABCD中,∠A与∠C互补,BE平分∠ABC,DF平分∠ADC,若BE∥DF,求证:△DCF为直角三角形.
证明:∵在四边形ABCD中,∠A与∠C互补,
∴∠ABC+∠ADC=180°,
运用了整体思想
∵BE平分∠ABC,DF平分∠ADC,
∴∠CDF+∠EBF=90°,
∵BE∥DF,
∴∠EBF=∠CFD,
∴∠CDF+∠CFD=90°,
∴△DCF为直角三角形.
长风破浪会有时,直挂云帆济沧海
你还记得如何求三角形的外角和吗?
三角形的外角之和为3600
3×180°-180°= 360°
深入探究
那么,如何求四边形的外角和呢?
四边形的外角之和为360°
4×180°-360°=360°
长风破浪会有时,直挂云帆济沧海
知识点三:多边形的内角和与外角和的综合应用
(1)多边形的一个内角与该角的外角互补.
(2)注意灵活应用多边形的内角和公式与外角和等于360°,可快速解题.
长风破浪会有时,直挂云帆济沧海
若一个正多边形的每一个外角都是30°,则这个正多边形的内角和的度数等于 .
一个正多边形的内角和为540°,则这个正多边形的每一个外角等于 .
1 800°
72°
(人教8上P25、北师8下P156)(2022云南模拟)已知一个多边形的内角和等于这个多边形外角和的2倍,则这个多边形的边数是 .
6
长风破浪会有时,直挂云帆济沧海
思维拓展
1、如图,求∠1+∠2+∠3+∠4+∠5+∠6+∠7的度数.
解:如图,
∵∠3+∠4=∠8+∠9,
∴∠1+∠2+∠3+∠4+∠5+∠6+∠7=∠1+∠2+∠8+∠9+∠5+∠6+∠7=五边形的内角和=540°.
8
9
长风破浪会有时,直挂云帆济沧海
小结:正多边形的外角和是360°,且这个正多边形的每个外角相等.
(2022成都二模)正多边形的一个外角的度数为72°,则这个正多边形的边数为( )
A.4 B.5
C.6 D.7
B
长风破浪会有时,直挂云帆济沧海
小结归纳
1.多边形的内角和公式:
(n-2)×180°.
2.多边形边数增加1,内角和增加180°
3.正多边形的每一个内角的度数:
长风破浪会有时,直挂云帆济沧海
能力提升
1、 已知一个多边形的每个内角与外角的比都是7:2,求这个多边形的边数.
解:设这个多边形的内角为7x °,外角为2x°,
根据题意得:
7x+2x=180,
解得x=20.
即每个内角是140 °,每个外角是40 °.
360° ÷40 °=9.
答:这个多边形是九边形.
长风破浪会有时,直挂云帆济沧海
能力提升
2、 一个多边形的内角和为1800°,截去一个角后,求得到的多边形的内角和.
解:∵1800÷180=10,
∴原多边形边数为10+2=12.
∵一个多边形截去一个内角后,边数可能减1,可能不变,也可能加1,
∴新多边形的边数可能是11,12,13,
∴新多边形的内角和可能是1620°,1800°,1980°.
长风破浪会有时,直挂云帆济沧海
课后作业
今天我们收获了哪些知识?
1.说一说多边形内角和公式?
2.在探究多边形内角和公式中,连接对角线起到什么作用?
3.多边形的外角和等于多少?
4.正多边形的一个外角和一个内角的公式是什么?
人教版八年级数学上册
11.3.2 多边形的内角和
一、掌握多边形内角和公式。
二、能根据已知内角和求多边形边数和已知多边形边数求内角和。
三、理解多边形外角和。
学习目标
长风破浪会有时,直挂云帆济沧海
问题1:任意四边形的内角和是多少度呢?
问题2:你能利用三角形内角和的知识验证你的猜想吗?
360°
讲授新课
长风破浪会有时,直挂云帆济沧海
180 °×2 = 360°
A
B
C
D
A
B
D
C
B
D
A
B
D
C
B
D
A
B
D
C
B
D
提示:三角形是最简单的多边形,研究其它多边形可借助对角线将其分为若干个三角形
验一验
四边形的内角和等于360°
长风破浪会有时,直挂云帆济沧海
知识点1:多边形的内角和
合作探究
活动一:探索四边形、五边形、六边形内角和.
画一画
量一量
猜一猜
证一证
画一画
分析:
长风破浪会有时,直挂云帆济沧海
例1.如果一个四边形的一组对角互补,那么另一组对角有什么关系?
解:∵∠A+∠B+∠C+∠D=(4-2)×180°= 360°,
又∵∠A+∠C = 180°,
∴∠B+∠D = 360°-(∠A+∠C)= 180°.
如果四边形一组对角互补,那么另一组对角也互补.
A
C
D
B
典例精析
长风破浪会有时,直挂云帆济沧海
量出你画的三个图形的各个内角,并求出内角和.
多边形 四边形 五边形 六边形
内角和
量一量
猜一猜
360°
540°
720°
长风破浪会有时,直挂云帆济沧海
证一证
请用多种方法证明上述结论.
n 个三角形
多边形
未知
已知
以一个点为顶点连接对角线
连接内部一点与各顶点
连接边上任意一点与各顶点
分析:
长风破浪会有时,直挂云帆济沧海
如图,在四边形ABCD中,∠A与∠C互补,BE平分∠ABC,DF平分∠ADC,若BE∥DF,求证:△DCF为直角三角形.
证明:∵在四边形ABCD中,∠A与∠C互补,
∴∠ABC+∠ADC=180°,
运用了整体思想
∵BE平分∠ABC,DF平分∠ADC,
∴∠CDF+∠EBF=90°,
∵BE∥DF,
∴∠EBF=∠CFD,
∴∠CDF+∠CFD=90°,
∴△DCF为直角三角形.
长风破浪会有时,直挂云帆济沧海
你还记得如何求三角形的外角和吗?
三角形的外角之和为3600
3×180°-180°= 360°
深入探究
那么,如何求四边形的外角和呢?
四边形的外角之和为360°
4×180°-360°=360°
长风破浪会有时,直挂云帆济沧海
知识点三:多边形的内角和与外角和的综合应用
(1)多边形的一个内角与该角的外角互补.
(2)注意灵活应用多边形的内角和公式与外角和等于360°,可快速解题.
长风破浪会有时,直挂云帆济沧海
若一个正多边形的每一个外角都是30°,则这个正多边形的内角和的度数等于 .
一个正多边形的内角和为540°,则这个正多边形的每一个外角等于 .
1 800°
72°
(人教8上P25、北师8下P156)(2022云南模拟)已知一个多边形的内角和等于这个多边形外角和的2倍,则这个多边形的边数是 .
6
长风破浪会有时,直挂云帆济沧海
思维拓展
1、如图,求∠1+∠2+∠3+∠4+∠5+∠6+∠7的度数.
解:如图,
∵∠3+∠4=∠8+∠9,
∴∠1+∠2+∠3+∠4+∠5+∠6+∠7=∠1+∠2+∠8+∠9+∠5+∠6+∠7=五边形的内角和=540°.
8
9
长风破浪会有时,直挂云帆济沧海
小结:正多边形的外角和是360°,且这个正多边形的每个外角相等.
(2022成都二模)正多边形的一个外角的度数为72°,则这个正多边形的边数为( )
A.4 B.5
C.6 D.7
B
长风破浪会有时,直挂云帆济沧海
小结归纳
1.多边形的内角和公式:
(n-2)×180°.
2.多边形边数增加1,内角和增加180°
3.正多边形的每一个内角的度数:
长风破浪会有时,直挂云帆济沧海
能力提升
1、 已知一个多边形的每个内角与外角的比都是7:2,求这个多边形的边数.
解:设这个多边形的内角为7x °,外角为2x°,
根据题意得:
7x+2x=180,
解得x=20.
即每个内角是140 °,每个外角是40 °.
360° ÷40 °=9.
答:这个多边形是九边形.
长风破浪会有时,直挂云帆济沧海
能力提升
2、 一个多边形的内角和为1800°,截去一个角后,求得到的多边形的内角和.
解:∵1800÷180=10,
∴原多边形边数为10+2=12.
∵一个多边形截去一个内角后,边数可能减1,可能不变,也可能加1,
∴新多边形的边数可能是11,12,13,
∴新多边形的内角和可能是1620°,1800°,1980°.
长风破浪会有时,直挂云帆济沧海
课后作业
今天我们收获了哪些知识?
1.说一说多边形内角和公式?
2.在探究多边形内角和公式中,连接对角线起到什么作用?
3.多边形的外角和等于多少?
4.正多边形的一个外角和一个内角的公式是什么?
