人教版七年级数学上册1.2.1有理数 导学案(知识清单+典型例题+巩固提升)(含解析)
文档属性
| 名称 | 人教版七年级数学上册1.2.1有理数 导学案(知识清单+典型例题+巩固提升)(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 319.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-03 00:00:00 | ||
图片预览





文档简介
中小学教育资源及组卷应用平台
人教版七年级数学上册 1.2.1有理数 导学案
【知识清单】
1.有理数定义:正整数、0、负整数统称整数,正分数、负分数统称分数,整数和分数统称有理数。
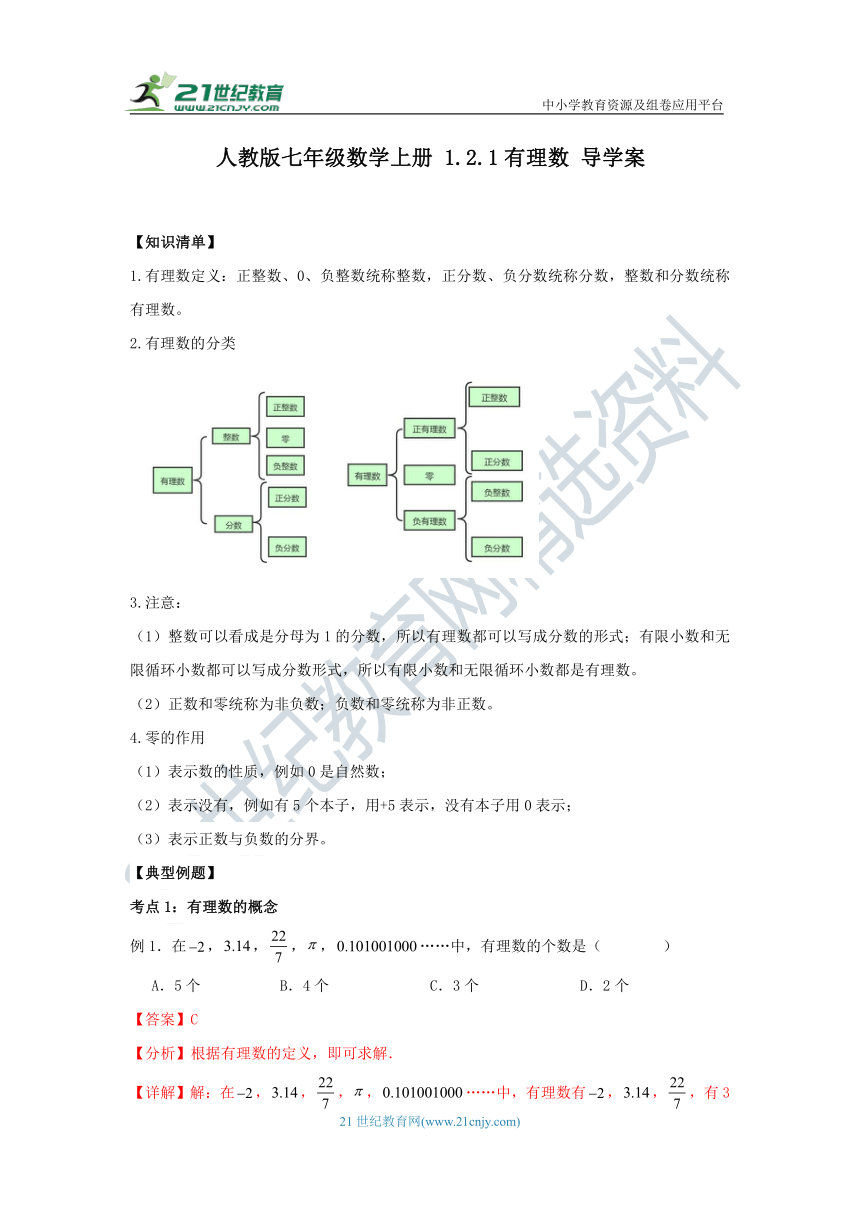
2.有理数的分类
3.注意:
(1)整数可以看成是分母为1的分数,所以有理数都可以写成分数的形式;有限小数和无限循环小数都可以写成分数形式,所以有限小数和无限循环小数都是有理数。
(2)正数和零统称为非负数;负数和零统称为非正数。
4.零的作用
(1)表示数的性质,例如0是自然数;
(2)表示没有,例如有5个本子,用+5表示,没有本子用0表示;
(3)表示正数与负数的分界。
【典型例题】
考点1:有理数的概念
例1.在,,,,……中,有理数的个数是( )
A.5个 B.4个 C.3个 D.2个
【答案】C
【分析】根据有理数的定义,即可求解.
【详解】解:在,,,,……中,有理数有,,,有3个,,……,不是有理数.
故选:C.
【点睛】本题主要考查了有理数的定义,熟练掌握整数和分数统称为有理数是解题的关键.
考点2:0的意义
例2.下列结论中正确的是( )
A.0既是正数,又是负数 B.0是最小的正数
C.0是最大的负数 D.0既不是正数,也不是负数
【答案】D
【分析】首先知道0这个实数的相关知识,根据0既不是正数,也不是负数作判断即可求解.
【详解】解:根据0既不是正数,也不是负数,
可以判断A、B、C都错误,D正确.
故选:D.
【点睛】本题主要考查0这个实数的知识点,解题关键熟练掌握①既不是正数,也不是负数;②是整数,也是有理数;③是最小的自然数;④是正数和负数的分界.
考点3:有理数的分类
例3.在,,,,,,,π中,负分数有( )
A.1个 B.2个 C.3个 D.4个
【答案】B
【分析】先找出负数,再找出分数和有限小数和无限循环小数即可.
【详解】解:在,,,,,,,π中,负分数有,,一共2个,
故选B.
【点睛】本题主要考查了有理数的分类,注意:分数包括分数和有限小数和无限循环小数.
考点4:带“非”字的有理数
例4.下列说法中,错误的是( )
A.有理数可分为正数和负数两类 B.有理数可分为整数和分数两类
C.0是有理数 D.非负整数就是自然数
【答案】A
【分析】根据有理数的分类方法进行逐一判断即可.
【详解】解:A、有理数可分为正数,0和负数三类,原说法错误,符合题意;
B、有理数可分为整数和分数两类,原说法正确,不符合题意;
C、0是有理数,原说法正确,不符合题意;
D、非负整数就是自然数,原说法正确,不符合题意;
故选A.
【点睛】本题主要考查了有理数的分类,熟知有理数的分类方法是解题的关键:有理数分为正数,0和负数,有理数又可以分为整数和分数,有理数还可以分为正有理数,负有理数和0.
【巩固提升】
一、选择题
1.下列各组数中,全部都是有理数的是( )
A.,, B., C., D.
2.接近于( )
A.珠穆朗玛峰的高度 B.三层住宅楼的高度
C.一层住宅楼的高度 D.一本书的厚度
3.关于“0”的说法,正确的是( )
A.是整数,也是正数 B.是整数,但不是正数
C.不是整数,是正数 D.是整数,但不是有理数
4.下列语句正确的是( )
①一个数前面加上“”号,这个数就是负数;②如果是正数,那么一定是负数;
③一个有理数不是正的就是负的;④表示没有温度;
A.0个 B.1个 C.2个 D.3个
5.下列各数:,,0,,,11中,负数有( )
A.2个 B.3个 C.4个 D.5个
6.下列说法正确的是( )
A.所有的整数都是正数 B.整数、0和分数统称为有理数
C.0是最小的有理数 D.是最大的负整数
7.在,,,0,,2,,.这八个有理数中非负数有( )
A.4个 B.5个 C.6个 D.7个
8.在这几个数中,是非负数的有( )
A.个 B.个 C.个 D.个
二、填空题
9.一个人唱《可可托海的牧羊人》需要5分40秒,全班50人合唱需要 .
10.0既不是 ,也不是 .0是 和 的分界点.
11.下面几个数中:15,,0,,,,是有理数的是 .
12.在①;②;③ 0;④;⑤中,是非负数的是 (填序号)
三、解答题
13.把以下各数填入相应的集合里:,,,,,,,,,,,.
(1)正数集合:{ …};
(2)负数集合:{ …};
(3)正整数集合:{ …};
(4)负整数集合:{ …};
(5)非负数集合:{ …}.
14.“不是正数的数一定是负数,不是负教的数一定是正数”的说法对吗?为什么?
15.把下列各数填在相应的集合内:
.
正有理数集合{ …};
负分数集合 { …};
整数集合 { …}.
16.把下列各数填在相应的大括号里.
,4,,,,,,,0,.
(1)整数集合{ …}
(2)分数集合{ …}
(3)非负数集合{ …}
(4)正有理数集合{ …}
(5)负有理数集合{ …}
参考答案
1.C
【分析】有理数是整数与分数的统称,即有限小数和无限循环小数是有理数,由此即可判断选项.
【详解】解:A.都是整数,属于有理数,是无理数,
此选项不符合题意;
B.是无理数,,2.3是有理数,
此选项不符合题意;
C.,,都是有理数,
此选项符合题意;
D.是无理数,是有理数,
此选项不符合题意;
故选:C.
【点睛】本题主要考查了有理数,解题的关键是了解有理数的分类.
2.D
【分析】根据数学常识求解即可.
【详解】解:接近一本书的厚度,
故选:D.
【点睛】此题考查了数学常识,解题的关键是熟练掌握以上知识点.
3.B
【分析】根据0既不是正数也不是负数,0是有理数也是整数,据此对各选项逐一判断即可.
【详解】解:A.0是整数,不是正数,则A选项错误,故A选项不符合题意;
B.0是整数,不是正数,则B选项正确,故B选项符合题意;
C.0是整数,不是正数,则C选项错误,故C选项不符合题意;
D.0是整数,也是有理数,则D选项错误,故D选项不符合题意,
故选B.
【点睛】本题主要考查了有理数的概念,0的特殊规定:0既不是正数也不是负数,0是有理数也是整数.熟练记忆是解决本题的关键.
4.B
【分析】根据正负数的定义和0的意义进行逐一判断即可.
【详解】解:①一个正数前面加上“”号,这个数就是负数,说法错误;
②如果是正数,那么一定是负数,说法正确;
③0是有理数,但是0既不是正数也不是负数,说法错误;
④表示有温度,说法错误;
故选B.
【点睛】本题主要考查了正负数的定义和0的意义,熟知相关知识是解题的关键.
5.B
【分析】根据负数的定义及常见负数形式即可得到答案.
【详解】解:,,0,,,11中,负数有,,,共计3个,
故选:B.
【点睛】本题考查负数定义,熟记常见负数的形式进行判断是解决问题的关键.
6.D
【分析】根据有理数的相关知识逐一判断即可.
【详解】解:A.整数包括正整数、负整数和0,则A错误,故A选项不符合题意;
B.整数包含了0,则B错误,故B选项不符合题意;
C.负数比0小,且是有理数,则C错误,故C选项不符合题意;
D.是最大的负整数,则D正确,故D选项符合题意,
故选D.
【点睛】本题考查了有理数,熟练掌握有理数的相关知识点是解题的关键.
7.B
【分析】正数与0为非负数,根据非负数的概念逐一分析即可得到答案.
【详解】解:在,,,0,,2,,.这八个数中,
非负数为,0,,2,有5个.
故选:B.
【点睛】本题考查的是有理数的分类,带“非”字的有理数,理解概念是解本题的关键.
8.B
【分析】直接利用非负数定义判断即可得出答案.
【详解】解:根据非负数的定义,非负数包含正数和零,
所以在这七个数中,是非负数的有共个.
故选:.
【点睛】本题考查了有理数的分类,解题的关键是正确掌握有理数的分类,非负数的定义.
9.5分40秒
【分析】根据题意和数学常识求解即可.
【详解】解:50个人合唱这首歌用的时间和一人唱这首歌用的时间相同,都是5分40秒.
故答案为:5分40秒.
【点睛】此题考查了数学常识,解题的关键是熟练掌握以上知识点.
10. 正数/负数 负数/正数 正数/负数 负数/正数
【分析】根据0的意义求解即可.
【详解】解:0既不是正数,也不是负数,0是正数和负数的分界点,
故答案为:正数;负数;正数;负数.
【点睛】本题主要考查了0的意义,熟知0的意义是解题的关键.
11.15,,0,,
【分析】整数和分数统称有理数,据此判断即可.
【详解】解:15,0是整数,
, , 是分数,
∴有理数为:15,,0,,.
故答案为:15,,0,,.
【点睛】本题考查了有理数的分类,明确不是有理数是解题的关键.
12.②③④
【分析】根据非负数包含正数和零,逐一进行判断即可得到答案.
【详解】解:因为,
所以,在①;②;③ 0;④;⑤中,是非负数的是:②;③ 0;④,
故答案为:②③④.
【点睛】本题考查了有理数的分类,熟练掌握非负数包含正数和零是解题关键.
13.(1),,,,,
(2),,,,
(3),
(4),
(5),,,,,,
【分析】(1)根据正数的定义:像、、等大于的数叫做正数即可解答;
(2)根据负数的定义:像、、、等在正数前面加“”号的数叫做负数即可解答;
(3)根据正整数的定义:除了以外的自然数叫做正整数即可解答;
(4)根据负整数的定义:在自然数前面加上负号所得的数叫做负整数即可解答;
(5)根据非负整数的定义: 正整数和零统称非负整数即可解答.
【详解】(1)解:正数集合:{,,,,,…};
故答案为:,,,,,;
(2)解:负数集合:{,,,,…};
故答案为:,,,,;
(3)解:正整数集合:{,…};
故答案为:,;
(4)解:负整数集合:{,…};
故答案为:,;
(5)解:非负数集合:{,,,,,,…}.
故答案为:,,,,,,.
【点睛】本题考查了正数的定义,负数的定义,正整数的定义,负整数的定义,非负整数的定义,熟记对应定义是解题的关键.
14.不对,因为0既不是正数也不是负数.
【分析】举反例进行说明即可.
【详解】不对.因为0既不是正数也不是负数.
【点睛】本题主要考查了0的意义,掌握“0既不是正数也不是负数”是解题的关键.
15.
【分析】根据有理数的分类进行填空即可.
【详解】解:正有理数集合{ …};
负分数集合 { …};
整数集合 {…}.
故答案为:.
【点睛】本题考查了有理数,掌握有理数的分类是解题的关键.
16.(1)见解析
(2)见解析
(3)见解析
(4)见解析
(5)见解析
【分析】按照有理数的分类解答即可.
【详解】(1)解:整数集合{,4,,,0,…}
(2)分数集合{,,,,…}
(3)非负数集合{4,,,,,0,,…}
(4)正有理数集合{4,,,,,…}
(5)负有理数集合{,,,…}
【点睛】本题考查了有理数,认真掌握正数、负数、整数、分数、正有理数、负有理数、非负数的定义与特点.注意整数和正数的区别,注意0是整数,但不是正数.
21世纪教育网(www.21cnjy.com)
人教版七年级数学上册 1.2.1有理数 导学案
【知识清单】
1.有理数定义:正整数、0、负整数统称整数,正分数、负分数统称分数,整数和分数统称有理数。
2.有理数的分类
3.注意:
(1)整数可以看成是分母为1的分数,所以有理数都可以写成分数的形式;有限小数和无限循环小数都可以写成分数形式,所以有限小数和无限循环小数都是有理数。
(2)正数和零统称为非负数;负数和零统称为非正数。
4.零的作用
(1)表示数的性质,例如0是自然数;
(2)表示没有,例如有5个本子,用+5表示,没有本子用0表示;
(3)表示正数与负数的分界。
【典型例题】
考点1:有理数的概念
例1.在,,,,……中,有理数的个数是( )
A.5个 B.4个 C.3个 D.2个
【答案】C
【分析】根据有理数的定义,即可求解.
【详解】解:在,,,,……中,有理数有,,,有3个,,……,不是有理数.
故选:C.
【点睛】本题主要考查了有理数的定义,熟练掌握整数和分数统称为有理数是解题的关键.
考点2:0的意义
例2.下列结论中正确的是( )
A.0既是正数,又是负数 B.0是最小的正数
C.0是最大的负数 D.0既不是正数,也不是负数
【答案】D
【分析】首先知道0这个实数的相关知识,根据0既不是正数,也不是负数作判断即可求解.
【详解】解:根据0既不是正数,也不是负数,
可以判断A、B、C都错误,D正确.
故选:D.
【点睛】本题主要考查0这个实数的知识点,解题关键熟练掌握①既不是正数,也不是负数;②是整数,也是有理数;③是最小的自然数;④是正数和负数的分界.
考点3:有理数的分类
例3.在,,,,,,,π中,负分数有( )
A.1个 B.2个 C.3个 D.4个
【答案】B
【分析】先找出负数,再找出分数和有限小数和无限循环小数即可.
【详解】解:在,,,,,,,π中,负分数有,,一共2个,
故选B.
【点睛】本题主要考查了有理数的分类,注意:分数包括分数和有限小数和无限循环小数.
考点4:带“非”字的有理数
例4.下列说法中,错误的是( )
A.有理数可分为正数和负数两类 B.有理数可分为整数和分数两类
C.0是有理数 D.非负整数就是自然数
【答案】A
【分析】根据有理数的分类方法进行逐一判断即可.
【详解】解:A、有理数可分为正数,0和负数三类,原说法错误,符合题意;
B、有理数可分为整数和分数两类,原说法正确,不符合题意;
C、0是有理数,原说法正确,不符合题意;
D、非负整数就是自然数,原说法正确,不符合题意;
故选A.
【点睛】本题主要考查了有理数的分类,熟知有理数的分类方法是解题的关键:有理数分为正数,0和负数,有理数又可以分为整数和分数,有理数还可以分为正有理数,负有理数和0.
【巩固提升】
一、选择题
1.下列各组数中,全部都是有理数的是( )
A.,, B., C., D.
2.接近于( )
A.珠穆朗玛峰的高度 B.三层住宅楼的高度
C.一层住宅楼的高度 D.一本书的厚度
3.关于“0”的说法,正确的是( )
A.是整数,也是正数 B.是整数,但不是正数
C.不是整数,是正数 D.是整数,但不是有理数
4.下列语句正确的是( )
①一个数前面加上“”号,这个数就是负数;②如果是正数,那么一定是负数;
③一个有理数不是正的就是负的;④表示没有温度;
A.0个 B.1个 C.2个 D.3个
5.下列各数:,,0,,,11中,负数有( )
A.2个 B.3个 C.4个 D.5个
6.下列说法正确的是( )
A.所有的整数都是正数 B.整数、0和分数统称为有理数
C.0是最小的有理数 D.是最大的负整数
7.在,,,0,,2,,.这八个有理数中非负数有( )
A.4个 B.5个 C.6个 D.7个
8.在这几个数中,是非负数的有( )
A.个 B.个 C.个 D.个
二、填空题
9.一个人唱《可可托海的牧羊人》需要5分40秒,全班50人合唱需要 .
10.0既不是 ,也不是 .0是 和 的分界点.
11.下面几个数中:15,,0,,,,是有理数的是 .
12.在①;②;③ 0;④;⑤中,是非负数的是 (填序号)
三、解答题
13.把以下各数填入相应的集合里:,,,,,,,,,,,.
(1)正数集合:{ …};
(2)负数集合:{ …};
(3)正整数集合:{ …};
(4)负整数集合:{ …};
(5)非负数集合:{ …}.
14.“不是正数的数一定是负数,不是负教的数一定是正数”的说法对吗?为什么?
15.把下列各数填在相应的集合内:
.
正有理数集合{ …};
负分数集合 { …};
整数集合 { …}.
16.把下列各数填在相应的大括号里.
,4,,,,,,,0,.
(1)整数集合{ …}
(2)分数集合{ …}
(3)非负数集合{ …}
(4)正有理数集合{ …}
(5)负有理数集合{ …}
参考答案
1.C
【分析】有理数是整数与分数的统称,即有限小数和无限循环小数是有理数,由此即可判断选项.
【详解】解:A.都是整数,属于有理数,是无理数,
此选项不符合题意;
B.是无理数,,2.3是有理数,
此选项不符合题意;
C.,,都是有理数,
此选项符合题意;
D.是无理数,是有理数,
此选项不符合题意;
故选:C.
【点睛】本题主要考查了有理数,解题的关键是了解有理数的分类.
2.D
【分析】根据数学常识求解即可.
【详解】解:接近一本书的厚度,
故选:D.
【点睛】此题考查了数学常识,解题的关键是熟练掌握以上知识点.
3.B
【分析】根据0既不是正数也不是负数,0是有理数也是整数,据此对各选项逐一判断即可.
【详解】解:A.0是整数,不是正数,则A选项错误,故A选项不符合题意;
B.0是整数,不是正数,则B选项正确,故B选项符合题意;
C.0是整数,不是正数,则C选项错误,故C选项不符合题意;
D.0是整数,也是有理数,则D选项错误,故D选项不符合题意,
故选B.
【点睛】本题主要考查了有理数的概念,0的特殊规定:0既不是正数也不是负数,0是有理数也是整数.熟练记忆是解决本题的关键.
4.B
【分析】根据正负数的定义和0的意义进行逐一判断即可.
【详解】解:①一个正数前面加上“”号,这个数就是负数,说法错误;
②如果是正数,那么一定是负数,说法正确;
③0是有理数,但是0既不是正数也不是负数,说法错误;
④表示有温度,说法错误;
故选B.
【点睛】本题主要考查了正负数的定义和0的意义,熟知相关知识是解题的关键.
5.B
【分析】根据负数的定义及常见负数形式即可得到答案.
【详解】解:,,0,,,11中,负数有,,,共计3个,
故选:B.
【点睛】本题考查负数定义,熟记常见负数的形式进行判断是解决问题的关键.
6.D
【分析】根据有理数的相关知识逐一判断即可.
【详解】解:A.整数包括正整数、负整数和0,则A错误,故A选项不符合题意;
B.整数包含了0,则B错误,故B选项不符合题意;
C.负数比0小,且是有理数,则C错误,故C选项不符合题意;
D.是最大的负整数,则D正确,故D选项符合题意,
故选D.
【点睛】本题考查了有理数,熟练掌握有理数的相关知识点是解题的关键.
7.B
【分析】正数与0为非负数,根据非负数的概念逐一分析即可得到答案.
【详解】解:在,,,0,,2,,.这八个数中,
非负数为,0,,2,有5个.
故选:B.
【点睛】本题考查的是有理数的分类,带“非”字的有理数,理解概念是解本题的关键.
8.B
【分析】直接利用非负数定义判断即可得出答案.
【详解】解:根据非负数的定义,非负数包含正数和零,
所以在这七个数中,是非负数的有共个.
故选:.
【点睛】本题考查了有理数的分类,解题的关键是正确掌握有理数的分类,非负数的定义.
9.5分40秒
【分析】根据题意和数学常识求解即可.
【详解】解:50个人合唱这首歌用的时间和一人唱这首歌用的时间相同,都是5分40秒.
故答案为:5分40秒.
【点睛】此题考查了数学常识,解题的关键是熟练掌握以上知识点.
10. 正数/负数 负数/正数 正数/负数 负数/正数
【分析】根据0的意义求解即可.
【详解】解:0既不是正数,也不是负数,0是正数和负数的分界点,
故答案为:正数;负数;正数;负数.
【点睛】本题主要考查了0的意义,熟知0的意义是解题的关键.
11.15,,0,,
【分析】整数和分数统称有理数,据此判断即可.
【详解】解:15,0是整数,
, , 是分数,
∴有理数为:15,,0,,.
故答案为:15,,0,,.
【点睛】本题考查了有理数的分类,明确不是有理数是解题的关键.
12.②③④
【分析】根据非负数包含正数和零,逐一进行判断即可得到答案.
【详解】解:因为,
所以,在①;②;③ 0;④;⑤中,是非负数的是:②;③ 0;④,
故答案为:②③④.
【点睛】本题考查了有理数的分类,熟练掌握非负数包含正数和零是解题关键.
13.(1),,,,,
(2),,,,
(3),
(4),
(5),,,,,,
【分析】(1)根据正数的定义:像、、等大于的数叫做正数即可解答;
(2)根据负数的定义:像、、、等在正数前面加“”号的数叫做负数即可解答;
(3)根据正整数的定义:除了以外的自然数叫做正整数即可解答;
(4)根据负整数的定义:在自然数前面加上负号所得的数叫做负整数即可解答;
(5)根据非负整数的定义: 正整数和零统称非负整数即可解答.
【详解】(1)解:正数集合:{,,,,,…};
故答案为:,,,,,;
(2)解:负数集合:{,,,,…};
故答案为:,,,,;
(3)解:正整数集合:{,…};
故答案为:,;
(4)解:负整数集合:{,…};
故答案为:,;
(5)解:非负数集合:{,,,,,,…}.
故答案为:,,,,,,.
【点睛】本题考查了正数的定义,负数的定义,正整数的定义,负整数的定义,非负整数的定义,熟记对应定义是解题的关键.
14.不对,因为0既不是正数也不是负数.
【分析】举反例进行说明即可.
【详解】不对.因为0既不是正数也不是负数.
【点睛】本题主要考查了0的意义,掌握“0既不是正数也不是负数”是解题的关键.
15.
【分析】根据有理数的分类进行填空即可.
【详解】解:正有理数集合{ …};
负分数集合 { …};
整数集合 {…}.
故答案为:.
【点睛】本题考查了有理数,掌握有理数的分类是解题的关键.
16.(1)见解析
(2)见解析
(3)见解析
(4)见解析
(5)见解析
【分析】按照有理数的分类解答即可.
【详解】(1)解:整数集合{,4,,,0,…}
(2)分数集合{,,,,…}
(3)非负数集合{4,,,,,0,,…}
(4)正有理数集合{4,,,,,…}
(5)负有理数集合{,,,…}
【点睛】本题考查了有理数,认真掌握正数、负数、整数、分数、正有理数、负有理数、非负数的定义与特点.注意整数和正数的区别,注意0是整数,但不是正数.
21世纪教育网(www.21cnjy.com)
