14.1.2幂的乘方课件
文档属性
| 名称 | 14.1.2幂的乘方课件 |  | |
| 格式 | zip | ||
| 文件大小 | 591.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-12-18 09:19:28 | ||
图片预览



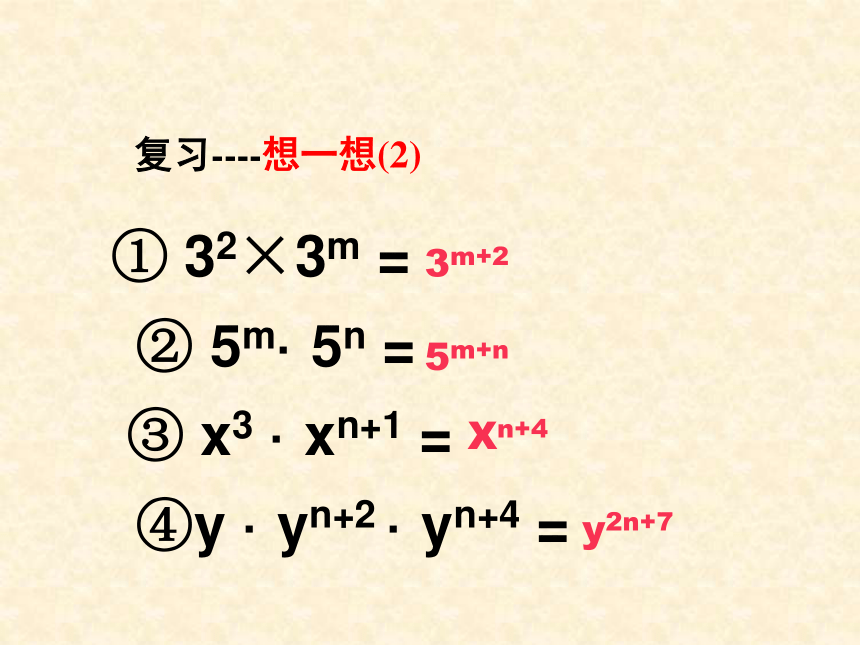

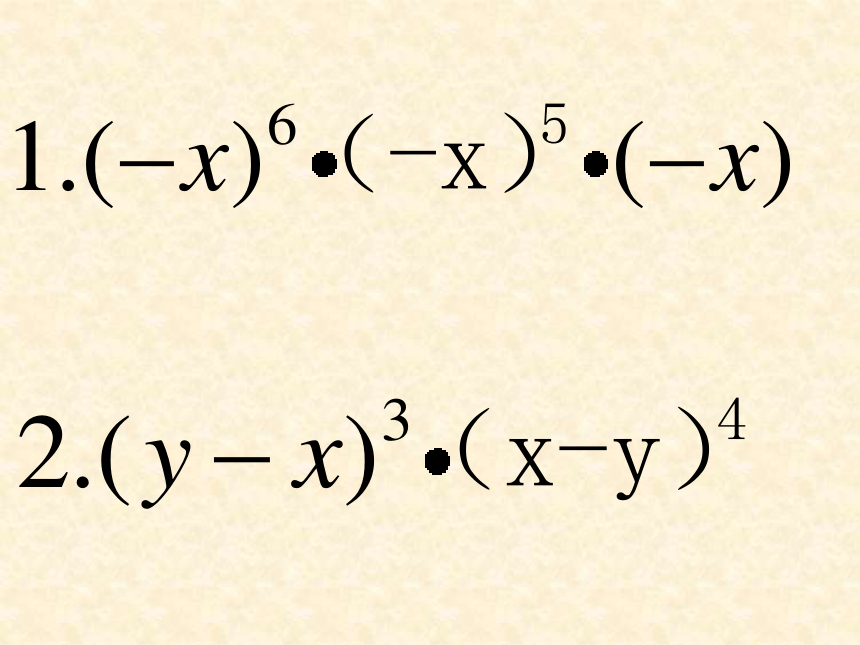





文档简介
课件31张PPT。15.1.2 幂的乘方同底数幂的乘法:
am · an = am+n (m、n为正整数)
同底数幂相乘,底数不变,指数相加。am · an · ap = am+n+p
( m、n、p为正整数)知识回顾中国奥委会为了把2008年北京奥运会办成一个环保的奥运会,做了一个统计:一平方千米的土地上,一年内从太阳得到的能量相当于燃烧 千克煤所产生的能量。那么 平方千米的土地上,一年内从太阳得到的能量相当于燃烧多少千克煤? 105解:108 ×105=?108复习----想一想(2) ① 32×3m = ② 5m· 5n = ③ x3 · xn+1 = ④y · yn+2 · yn+4 =3m+25m+ny2n+7Xn+4已知:am=2, an=3.
求am+n =?.解: am+n = am · an
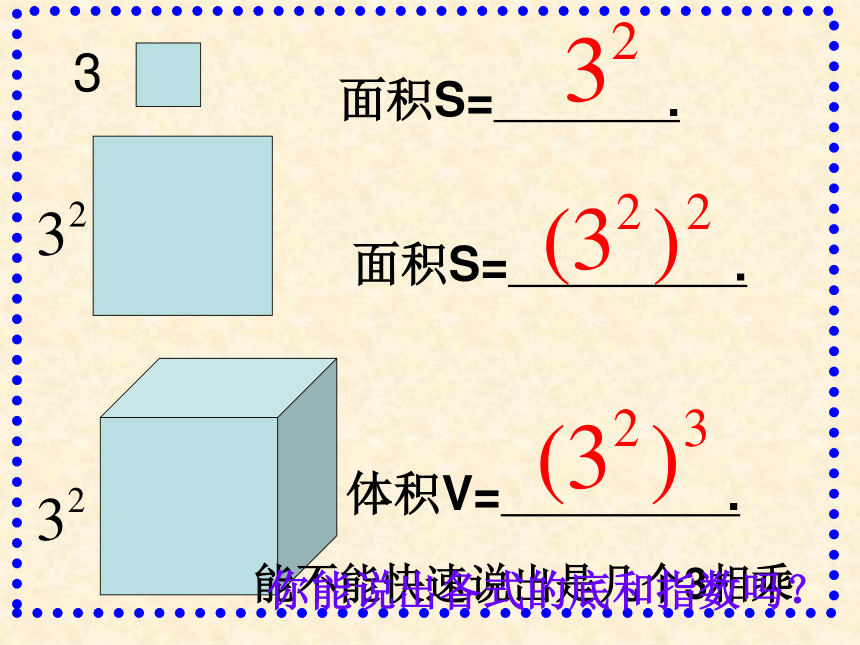
=2 × 3=6 深入探索----议一议判断下面计算是否正确,如有错误请改正。 (×)3面积S= .面积S= .能不能快速说出是几个3相乘体积V= .你能说出各式的底和指数吗?探究
根据乘方的意义及同底数幂的乘法填空,看看计算的结果有什么规律:
(32)3=32×32×32=3( );
(a2)3=a2×a2×a2=a ( ).
(am)3=am·am·am=a( ) (m是正整数). (3) 观察:这几道题有什么共同的特点呢?
计算的结果有什么规律吗? (1) (2) 猜想: (am)n=amn(m,n都是正整数).幂的乘方,底数 ,指数 。不变相乘如 (23)4=23×4=212 幂的乘方公式(am)n=amn(m,n都是正整数)即幂的乘方,底数不变,指数相乘.一般地,我们有am·an=am+n(m,n都是正整数)即同底数幂相乘,底数不变,指数相加.(1) (103)5 (2) (a4)4
(3) (am)2 (4) -(x4)3例2:计算:
(1) (103)5; (2) (a4)4; (3) (am)2; (4) -(x4)3.解: (1) (103)5=103Χ5 = 1015 ; (2) (a4)4=a4Χ4=a16;
(3) (am)2= a mΧ 2 = a 2m ; (4) -(x4)3 = - x 4x3 = - x12 . 幂的乘方法则(重点)
例 2:计算:(1)(x2)3;
(3)(a3)2-(a2)3;(2)-(x9)8;
(4)(a2)3·a5.思路导引:运用幂的乘方法则,运算时要先确定符号.幂的乘方的逆运算:
(1)x13·x7=x( )=( )5=( )4=( )10;
(2)a2m =( )2 =( )m
(m为正整数).
20x4x5 x2ama2幂的乘方法则的逆用1.(m2)3·m4等于()BA.m9B.m10C.m12D.m142.计算:(1)[(x+y)2]6=____________;
(2)a8+(a2)4=____________.2a83.已知 x2n=3,则(xn)4=________.9点拔:(xn)4=x4n=(x2n)2=32=9.(x+y)12
4.已知 10a=5,10b=6,则 102a+103b的值为________.
241点拨:102a+103b=(10a)2+(10b)3=52+63=241.例 2:已知 ax=3,ay=2,试求 a2x+3y 【规律总结】对于幂的乘方与同底数幂的乘法的混合运算,
先算乘方,再算同底数幂的乘法;幂的乘方与加减混合运算时,
先乘方,后加减,注意合并同类项.的值. 幂的乘方法则的逆用
amn=(am)n=(an)m,即 x6=(x2)3=(x3)2.-(x2)3 八年级 数学= -x2×3= -x6 ;符号怎么办?(- x2)3 = -x2×3= -x6 ;-(x3)2 = -x3×2= - x6 ;(- x3)2 = x2×3= x6 ;我是法官我来判! (×)(×) (×)我是法官我来判! (2) a6 · a4 = a24 (x3)3 = x6元芳,你怎么看?乘法乘方不变不变指数
相加指数
相乘⑵(a-b)3[(a-b)3]2⑶[(x-y)2]2[(y-x)2]3小结:今天,我们学到了什么?底数 ,指数 。不变相加 底数 ,指数 。不变相乘 2. 已知3×9n=37,求:n的值.1. 已知53n=25,求:n的值.八年级 数学练一练多重乘方也具有这一性质在255,344,433,522这四个幂中,
数值最大的一个是———。解:255=25×11=(25)11=3211344=34×11=(34)11=8111433=43×11=(43)11=6411522=52×11=(52)11=2511所以数值最大的一个是______344拓展:深入探索----议一议2(1)已知2x+5y-3=0,求 4x · 32y的值(2)已知 2x =a, 2y =b,求 22x+3y 的值(3)已知 22n+1 + 4n =48, 求 n 的值(4)比较375,2100的大小(5)若(9n)2 = 38 ,则n为______相信你准能做对哟练习
计算:
(103)3; (2) (x3)2;
(3) - ( xm )5 ; (4) (a2 )3? a5;
(5) 0.254?82; (6) 8?86?0.255;
(7) [(m-n)2]3+(m-n)3(n-m)3.1.已知,44?83=2x,求x的值.实践与创新再见
am · an = am+n (m、n为正整数)
同底数幂相乘,底数不变,指数相加。am · an · ap = am+n+p
( m、n、p为正整数)知识回顾中国奥委会为了把2008年北京奥运会办成一个环保的奥运会,做了一个统计:一平方千米的土地上,一年内从太阳得到的能量相当于燃烧 千克煤所产生的能量。那么 平方千米的土地上,一年内从太阳得到的能量相当于燃烧多少千克煤? 105解:108 ×105=?108复习----想一想(2) ① 32×3m = ② 5m· 5n = ③ x3 · xn+1 = ④y · yn+2 · yn+4 =3m+25m+ny2n+7Xn+4已知:am=2, an=3.
求am+n =?.解: am+n = am · an
=2 × 3=6 深入探索----议一议判断下面计算是否正确,如有错误请改正。 (×)3面积S= .面积S= .能不能快速说出是几个3相乘体积V= .你能说出各式的底和指数吗?探究
根据乘方的意义及同底数幂的乘法填空,看看计算的结果有什么规律:
(32)3=32×32×32=3( );
(a2)3=a2×a2×a2=a ( ).
(am)3=am·am·am=a( ) (m是正整数). (3) 观察:这几道题有什么共同的特点呢?
计算的结果有什么规律吗? (1) (2) 猜想: (am)n=amn(m,n都是正整数).幂的乘方,底数 ,指数 。不变相乘如 (23)4=23×4=212 幂的乘方公式(am)n=amn(m,n都是正整数)即幂的乘方,底数不变,指数相乘.一般地,我们有am·an=am+n(m,n都是正整数)即同底数幂相乘,底数不变,指数相加.(1) (103)5 (2) (a4)4
(3) (am)2 (4) -(x4)3例2:计算:
(1) (103)5; (2) (a4)4; (3) (am)2; (4) -(x4)3.解: (1) (103)5=103Χ5 = 1015 ; (2) (a4)4=a4Χ4=a16;
(3) (am)2= a mΧ 2 = a 2m ; (4) -(x4)3 = - x 4x3 = - x12 . 幂的乘方法则(重点)
例 2:计算:(1)(x2)3;
(3)(a3)2-(a2)3;(2)-(x9)8;
(4)(a2)3·a5.思路导引:运用幂的乘方法则,运算时要先确定符号.幂的乘方的逆运算:
(1)x13·x7=x( )=( )5=( )4=( )10;
(2)a2m =( )2 =( )m
(m为正整数).
20x4x5 x2ama2幂的乘方法则的逆用1.(m2)3·m4等于()BA.m9B.m10C.m12D.m142.计算:(1)[(x+y)2]6=____________;
(2)a8+(a2)4=____________.2a83.已知 x2n=3,则(xn)4=________.9点拔:(xn)4=x4n=(x2n)2=32=9.(x+y)12
4.已知 10a=5,10b=6,则 102a+103b的值为________.
241点拨:102a+103b=(10a)2+(10b)3=52+63=241.例 2:已知 ax=3,ay=2,试求 a2x+3y 【规律总结】对于幂的乘方与同底数幂的乘法的混合运算,
先算乘方,再算同底数幂的乘法;幂的乘方与加减混合运算时,
先乘方,后加减,注意合并同类项.的值. 幂的乘方法则的逆用
amn=(am)n=(an)m,即 x6=(x2)3=(x3)2.-(x2)3 八年级 数学= -x2×3= -x6 ;符号怎么办?(- x2)3 = -x2×3= -x6 ;-(x3)2 = -x3×2= - x6 ;(- x3)2 = x2×3= x6 ;我是法官我来判! (×)(×) (×)我是法官我来判! (2) a6 · a4 = a24 (x3)3 = x6元芳,你怎么看?乘法乘方不变不变指数
相加指数
相乘⑵(a-b)3[(a-b)3]2⑶[(x-y)2]2[(y-x)2]3小结:今天,我们学到了什么?底数 ,指数 。不变相加 底数 ,指数 。不变相乘 2. 已知3×9n=37,求:n的值.1. 已知53n=25,求:n的值.八年级 数学练一练多重乘方也具有这一性质在255,344,433,522这四个幂中,
数值最大的一个是———。解:255=25×11=(25)11=3211344=34×11=(34)11=8111433=43×11=(43)11=6411522=52×11=(52)11=2511所以数值最大的一个是______344拓展:深入探索----议一议2(1)已知2x+5y-3=0,求 4x · 32y的值(2)已知 2x =a, 2y =b,求 22x+3y 的值(3)已知 22n+1 + 4n =48, 求 n 的值(4)比较375,2100的大小(5)若(9n)2 = 38 ,则n为______相信你准能做对哟练习
计算:
(103)3; (2) (x3)2;
(3) - ( xm )5 ; (4) (a2 )3? a5;
(5) 0.254?82; (6) 8?86?0.255;
(7) [(m-n)2]3+(m-n)3(n-m)3.1.已知,44?83=2x,求x的值.实践与创新再见
