13.2画轴对称图形 同步练习 2023—2024学年人教版数学八年级上册(含答案)
文档属性
| 名称 | 13.2画轴对称图形 同步练习 2023—2024学年人教版数学八年级上册(含答案) | 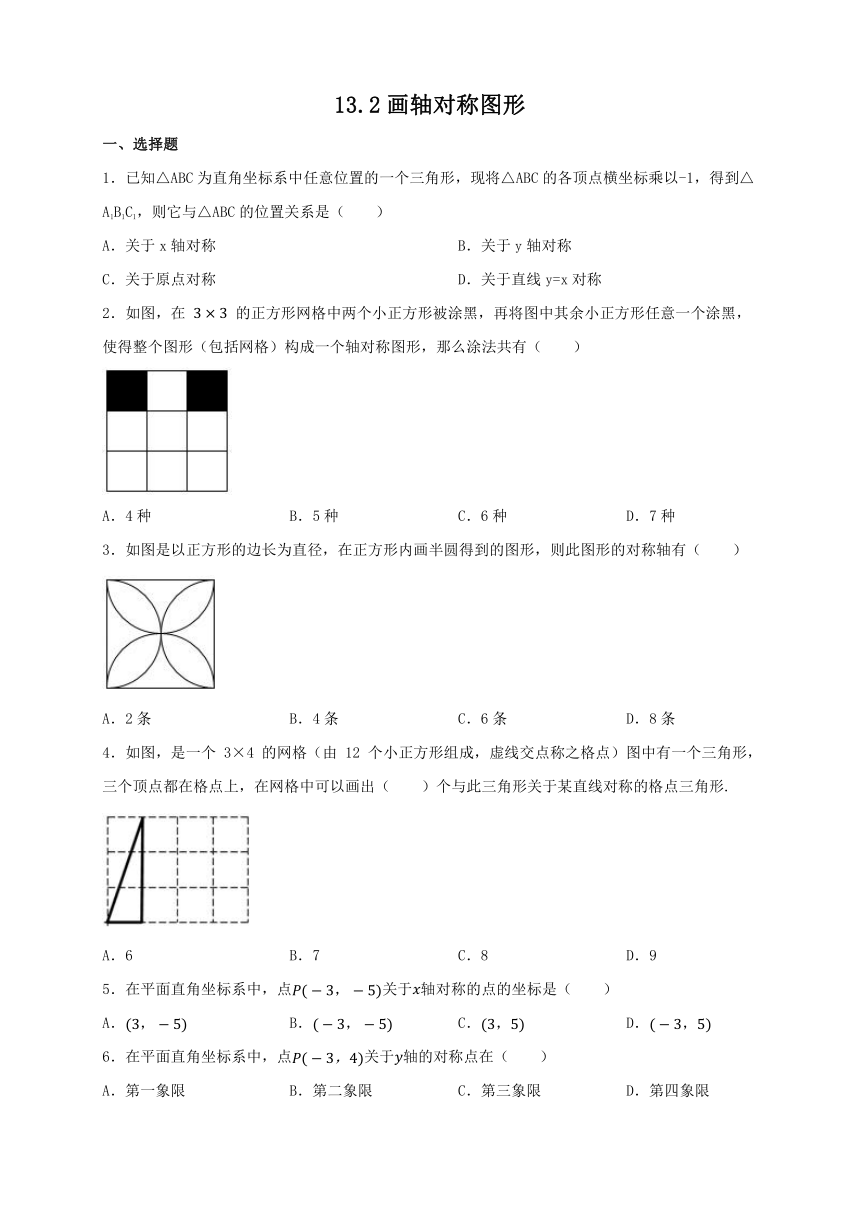 | |
| 格式 | docx | ||
| 文件大小 | 514.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-03 23:26:15 | ||
图片预览


文档简介
13.2画轴对称图形
一、选择题
1.已知△ABC为直角坐标系中任意位置的一个三角形,现将△ABC的各顶点横坐标乘以-1,得到△A1B1C1,则它与△ABC的位置关系是( )
A.关于x轴对称 B.关于y轴对称
C.关于原点对称 D.关于直线y=x对称
2.如图,在 的正方形网格中两个小正方形被涂黑,再将图中其余小正方形任意一个涂黑,使得整个图形(包括网格)构成一个轴对称图形,那么涂法共有( )
A.4种 B.5种 C.6种 D.7种
3.如图是以正方形的边长为直径,在正方形内画半圆得到的图形,则此图形的对称轴有( )
A.2条 B.4条 C.6条 D.8条
4.如图,是一个 3×4 的网格(由 12 个小正方形组成,虚线交点称之格点)图中有一个三角形,三个顶点都在格点上,在网格中可以画出( )个与此三角形关于某直线对称的格点三角形.
A.6 B.7 C.8 D.9
5.在平面直角坐标系中,点关于轴对称的点的坐标是( )
A. B. C. D.
6.在平面直角坐标系中,点关于轴的对称点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.已知点与关于x轴对称,则( )
A.1 B.0 C.4 D.2
8.如图,在直角坐标系中,各点坐标分别为,,.先作关于x轴成轴对称的,再把平移后得到.若,则点坐标为( )
A. B. C. D.
二、填空题
9.在4×4的方格中有五个同样大小的正方形如图摆放,移动其中一个正方形到空白方格中,与其余四个正方形组成的新图形是一个轴对称图形,这样的移法共有 种.
10.若点 位于第三象限,则点关于轴的对称点落在第 象限.
11.在平面直角坐标系中,点和关于 轴对称.
12.若点关于轴的对称点是点,则 .
13.如图,在平面直角坐标系中,△ABC关于直线m对称,直线m与x轴交点为(1,0),点C的坐标为(4,1),则点B的坐标为 .
三、解答题
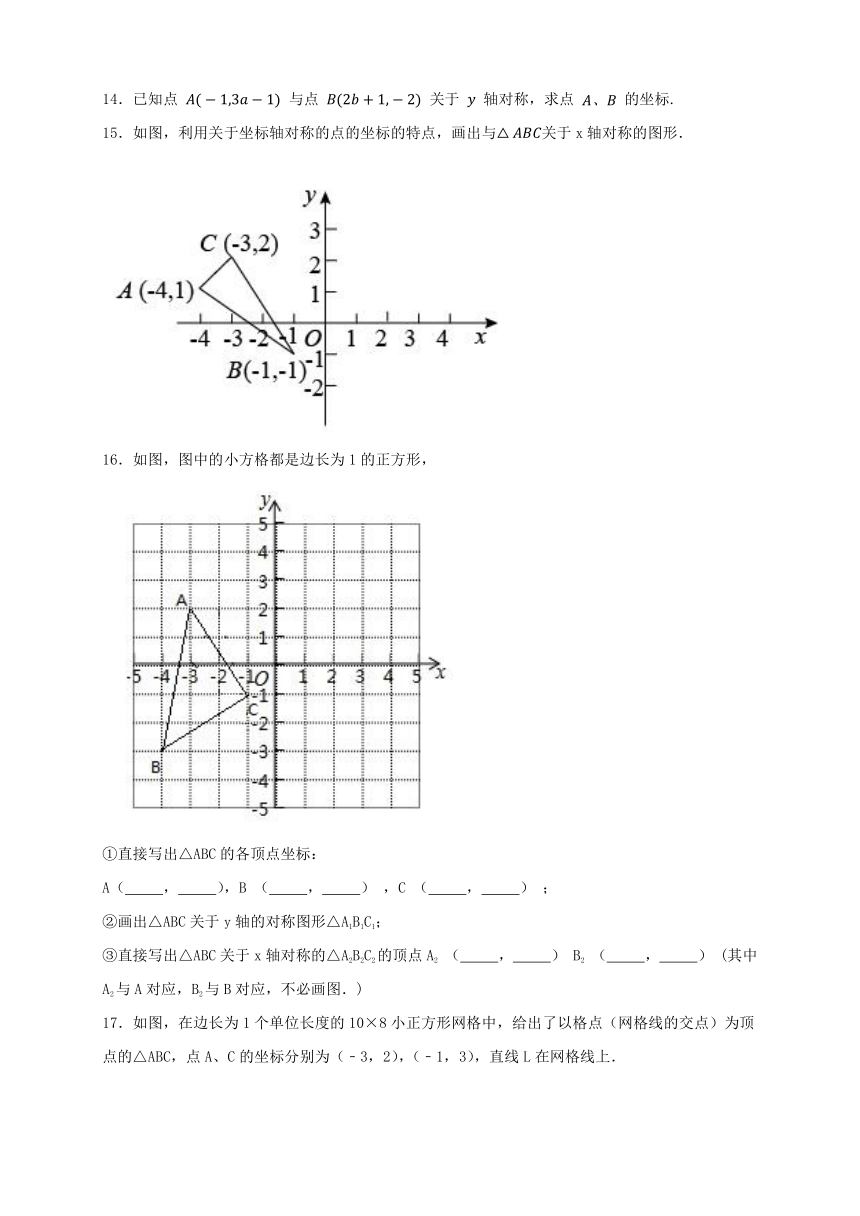
14.已知点 与点 关于 轴对称,求点 的坐标.
15.如图,利用关于坐标轴对称的点的坐标的特点,画出与关于x轴对称的图形.
16.如图,图中的小方格都是边长为1的正方形,
①直接写出△ABC的各顶点坐标:
A( , ),B ( , ) ,C ( , ) ;
②画出△ABC关于y轴的对称图形△A1B1C1;
③直接写出△ABC关于x轴对称的△A2B2C2的顶点A2 ( , ) B2 ( , ) (其中A2与A对应,B2与B对应,不必画图.)
17.如图,在边长为1个单位长度的10×8小正方形网格中,给出了以格点(网格线的交点)为顶点的△ABC,点A、C的坐标分别为(﹣3,2),(﹣1,3),直线L在网格线上.
(1)画出△ABC关于直线L对称的△A1B1C1;(点A1、B1、C1分别为点A、B、C的对应点)
(2)点D是ABC内部的格点,其关于直线L的对称点是D1,直接写出点D,D1的坐标.
(3)若点P(a,b)是△ABC内任意一点,其关于直线L的对称点是P1,求点P1的坐标.
18.如图,在平面直角坐标系中,、、.
(1)在图中作出关于y轴对称的图形;
(2)写出,的坐标;
(3)求出的面积;
参考答案
1.B
2.B
3.B
4.B
5.D
6.A
7.B
8.B
9.13
10.四
11.y(或纵)
12.-3
13.(-2,1)
14.解:∵点 与点 关于 轴对称,
∴ ,
解得 ,
∴ , ,
∴ .
15.解:A(-4,1)关于x轴对称点D(-4,-1),B(-1,-1)关于x轴对称点E(-1,1),C(-3,2)关于x轴对称点F(-3,-2),
在坐标系中描出点D(-4,-1),E(-1,1),F(-3,-2),
连接DE、EF、FD,
如图所示,△DEF就是△ABC关于x轴对称的图形.
16.解:①△ABC的各顶点坐标:A(﹣3,2)、B(﹣4,﹣3)、C(﹣1,﹣1);
故答案为:﹣3、2;﹣4、﹣3;﹣1、﹣1;
②如图,△A1B1C1即为所求,
③如图,△A2B2C2即为所求,A2坐标为(﹣3,﹣2)、B2坐标为(﹣4,3).
故答案为:﹣3、﹣2;﹣4、3.
17.(1)解:如图,根据轴对称的性质找到点,△A1B1C1即为所求;
(2)解:点D(-2,2),D1的坐标(4,2)
(3)解:根据两点关于直线对称,纵坐标相等,中点的横坐标为,则点P1的坐标(2-a,b)
18.(1)解:如图,即为所求.
(2)解:,
(3)解:
一、选择题
1.已知△ABC为直角坐标系中任意位置的一个三角形,现将△ABC的各顶点横坐标乘以-1,得到△A1B1C1,则它与△ABC的位置关系是( )
A.关于x轴对称 B.关于y轴对称
C.关于原点对称 D.关于直线y=x对称
2.如图,在 的正方形网格中两个小正方形被涂黑,再将图中其余小正方形任意一个涂黑,使得整个图形(包括网格)构成一个轴对称图形,那么涂法共有( )
A.4种 B.5种 C.6种 D.7种
3.如图是以正方形的边长为直径,在正方形内画半圆得到的图形,则此图形的对称轴有( )
A.2条 B.4条 C.6条 D.8条
4.如图,是一个 3×4 的网格(由 12 个小正方形组成,虚线交点称之格点)图中有一个三角形,三个顶点都在格点上,在网格中可以画出( )个与此三角形关于某直线对称的格点三角形.
A.6 B.7 C.8 D.9
5.在平面直角坐标系中,点关于轴对称的点的坐标是( )
A. B. C. D.
6.在平面直角坐标系中,点关于轴的对称点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.已知点与关于x轴对称,则( )
A.1 B.0 C.4 D.2
8.如图,在直角坐标系中,各点坐标分别为,,.先作关于x轴成轴对称的,再把平移后得到.若,则点坐标为( )
A. B. C. D.
二、填空题
9.在4×4的方格中有五个同样大小的正方形如图摆放,移动其中一个正方形到空白方格中,与其余四个正方形组成的新图形是一个轴对称图形,这样的移法共有 种.
10.若点 位于第三象限,则点关于轴的对称点落在第 象限.
11.在平面直角坐标系中,点和关于 轴对称.
12.若点关于轴的对称点是点,则 .
13.如图,在平面直角坐标系中,△ABC关于直线m对称,直线m与x轴交点为(1,0),点C的坐标为(4,1),则点B的坐标为 .
三、解答题
14.已知点 与点 关于 轴对称,求点 的坐标.
15.如图,利用关于坐标轴对称的点的坐标的特点,画出与关于x轴对称的图形.
16.如图,图中的小方格都是边长为1的正方形,
①直接写出△ABC的各顶点坐标:
A( , ),B ( , ) ,C ( , ) ;
②画出△ABC关于y轴的对称图形△A1B1C1;
③直接写出△ABC关于x轴对称的△A2B2C2的顶点A2 ( , ) B2 ( , ) (其中A2与A对应,B2与B对应,不必画图.)
17.如图,在边长为1个单位长度的10×8小正方形网格中,给出了以格点(网格线的交点)为顶点的△ABC,点A、C的坐标分别为(﹣3,2),(﹣1,3),直线L在网格线上.
(1)画出△ABC关于直线L对称的△A1B1C1;(点A1、B1、C1分别为点A、B、C的对应点)
(2)点D是ABC内部的格点,其关于直线L的对称点是D1,直接写出点D,D1的坐标.
(3)若点P(a,b)是△ABC内任意一点,其关于直线L的对称点是P1,求点P1的坐标.
18.如图,在平面直角坐标系中,、、.
(1)在图中作出关于y轴对称的图形;
(2)写出,的坐标;
(3)求出的面积;
参考答案
1.B
2.B
3.B
4.B
5.D
6.A
7.B
8.B
9.13
10.四
11.y(或纵)
12.-3
13.(-2,1)
14.解:∵点 与点 关于 轴对称,
∴ ,
解得 ,
∴ , ,
∴ .
15.解:A(-4,1)关于x轴对称点D(-4,-1),B(-1,-1)关于x轴对称点E(-1,1),C(-3,2)关于x轴对称点F(-3,-2),
在坐标系中描出点D(-4,-1),E(-1,1),F(-3,-2),
连接DE、EF、FD,
如图所示,△DEF就是△ABC关于x轴对称的图形.
16.解:①△ABC的各顶点坐标:A(﹣3,2)、B(﹣4,﹣3)、C(﹣1,﹣1);
故答案为:﹣3、2;﹣4、﹣3;﹣1、﹣1;
②如图,△A1B1C1即为所求,
③如图,△A2B2C2即为所求,A2坐标为(﹣3,﹣2)、B2坐标为(﹣4,3).
故答案为:﹣3、﹣2;﹣4、3.
17.(1)解:如图,根据轴对称的性质找到点,△A1B1C1即为所求;
(2)解:点D(-2,2),D1的坐标(4,2)
(3)解:根据两点关于直线对称,纵坐标相等,中点的横坐标为,则点P1的坐标(2-a,b)
18.(1)解:如图,即为所求.
(2)解:,
(3)解:
