2023—2024学年人教版数学八年级上册11.1与三角形有关的线段 同步练习 (含答案)
文档属性
| 名称 | 2023—2024学年人教版数学八年级上册11.1与三角形有关的线段 同步练习 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 113.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-04 06:22:51 | ||
图片预览


文档简介
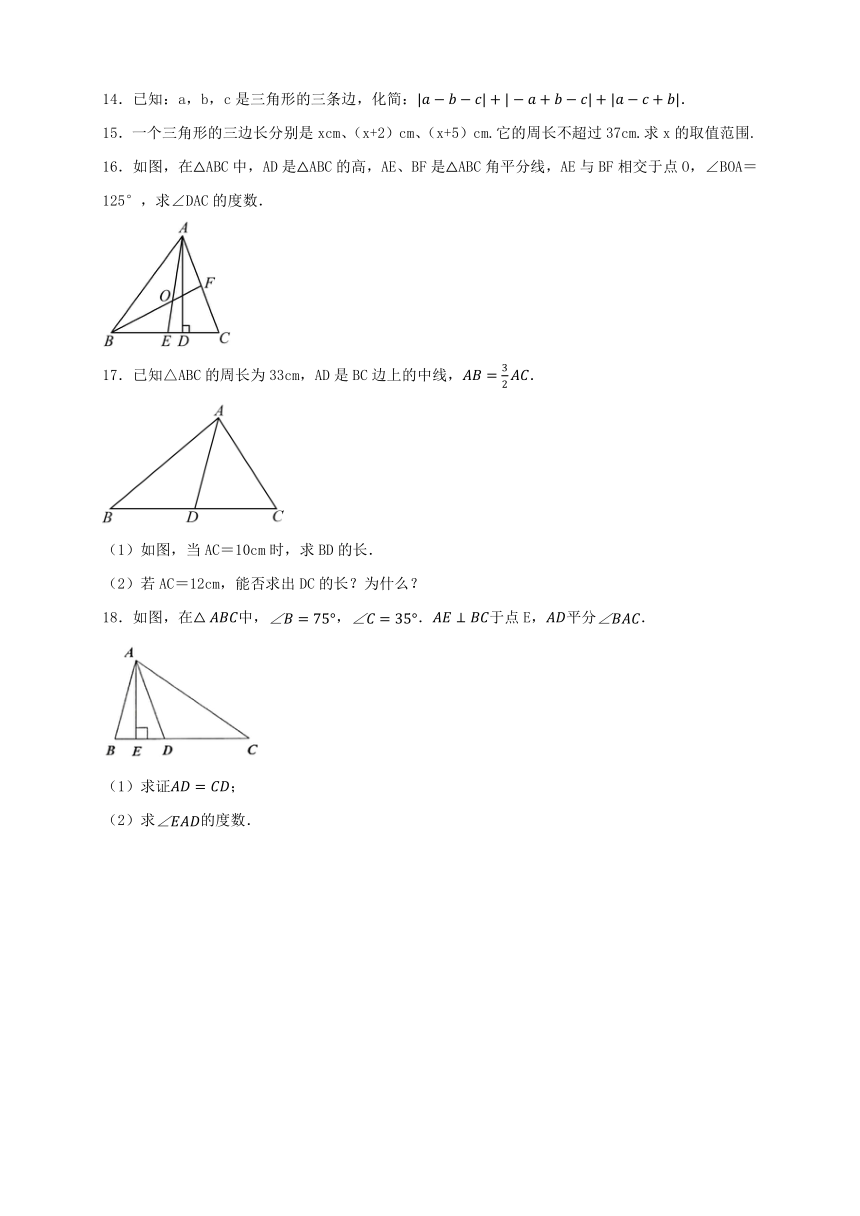
11.1与三角形有关的线段
一、选择题
1.已知一个三角形的两边长为1,3,则第三边可以是( )
A.2 B.3 C.4 D.5
2.长度分别为3cm,5cm,7cm,9cm的四根木棒,能搭成(首尾连接)三角形的个数为( )
A.1 B.2 C.3 D.4
3.王师傅用4根木条钉成一个四边形木架,如图,要使这个木架不变形,他至少还要再钉上几根木条?( )
A.0根 B.1根 C.2根 D.3根
4.下列各个图形中,是的高的是( )
A. B.
C. D.
5.周末李强和朋友到森林公园游玩,为测量园内湖岸A,B两点之间的距离,如图,李强在湖的一侧选取了一点O,测得OA=20m,OB=8m,则A,B间的距离可能是( )
A.10m B.22m C.30m D.32m
6.如图,AD是△ABC的中线,则下列结论正确的是( )
A.AB=AC B.BD=CD C.BD=AD D.AC=AD
7.如图,在△ABC中,AB=AC=5,BC=3,BD为中线,则△ABD与△BCD的周长之差为( )
A.1 B.2 C.3 D.4
8.如图,在中,已知点D、E、F分别为的中点,且,则阴影部分面积S是( )
A.1 B.2 C.3 D.4
二、填空题
9.在△ABC中,AB=6,BC=8,则AC的长x的取值范围是 。
10.如图,工人师傅在安装木制门框时,为防止变形常常钉上两根木条,这样做的依据是 .
11.一个三角形的两边长分别是3和7,且第三边长为奇数,这个三角形的最大周长是 ,
12.在中,AB=a,BC=b,的高AD与高CE的比是
13.如图,点D是中AB边上的点,点E是CD的中点,连接AE、BE,若的面积为8,则阴影部分的面积为 .
三、解答题
14.已知:a,b,c是三角形的三条边,化简:.
15.一个三角形的三边长分别是xcm、(x+2)cm、(x+5)cm.它的周长不超过37cm.求x的取值范围.
16.如图,在ABC中,AD是ABC的高,AE、BF是ABC角平分线,AE与BF相交于点O,∠BOA=125°,求∠DAC的度数.
17.已知△ABC的周长为33cm,AD是BC边上的中线,.
(1)如图,当AC=10cm时,求BD的长.
(2)若AC=12cm,能否求出DC的长?为什么?
18.如图,在中,,.于点E,平分.
(1)求证;
(2)求的度数.
参考答案
1.B
2.C
3.B
4.D
5.B
6.B
7.B
8.B
9.2<x<14
10.三角形具有稳定性
11.19
12.
13.4
14.解:∵a、b、c是三角形的三边长,
∴a-b-c<0,-a+b-c<0,a-c+b>0,
∴
=
=
=
15.解:∵一个三角形的三边长分别是xcm,(x+2)cm,(x+5)cm,它的周长不超过37cm,
∴ ,
解得:3<x≤10.
16.解:∵∠OAB+∠OBA+∠AOB=180°,∠AOB=125°,
∴∠OAB+∠OBA=180°﹣125°=55°,
∵AE、BF是△ABC角平分线,
∴∠OAB=∠BAC,∠OBA=∠ABC,
∴∠BAC+∠ABC=55°,
∴∠BAC+∠ABC=110°,
∵∠BAC+∠ABC+∠ACB=180°,
∴∠ACB=70°,
∵AD是△ABC的高,
∴∠ADC=90°,
∴∠DAC=90°﹣70°=20°.
17.(1)解:∵,AC=10cm,
∴AB=15cm.
又∵△ABC的周长是33cm,即
∴
∵AD是BC边上的中线,
∴.
(2)解:不能,理由如下:
∵,AC=12cm,
∴AB=18cm.
又∵△ABC的周长是33cm,
∴BC=3cm.
∵AC+BC=15cm<AB=18cm,
∴不能构成三角形ABC,
∴不能求出DC的长.
18.(1)证明:∵,,
∴,
∵AD平分,
∴,
∴,
∴;
(2)解:∵,
∴,
∵,
∴,
∴,
即.
一、选择题
1.已知一个三角形的两边长为1,3,则第三边可以是( )
A.2 B.3 C.4 D.5
2.长度分别为3cm,5cm,7cm,9cm的四根木棒,能搭成(首尾连接)三角形的个数为( )
A.1 B.2 C.3 D.4
3.王师傅用4根木条钉成一个四边形木架,如图,要使这个木架不变形,他至少还要再钉上几根木条?( )
A.0根 B.1根 C.2根 D.3根
4.下列各个图形中,是的高的是( )
A. B.
C. D.
5.周末李强和朋友到森林公园游玩,为测量园内湖岸A,B两点之间的距离,如图,李强在湖的一侧选取了一点O,测得OA=20m,OB=8m,则A,B间的距离可能是( )
A.10m B.22m C.30m D.32m
6.如图,AD是△ABC的中线,则下列结论正确的是( )
A.AB=AC B.BD=CD C.BD=AD D.AC=AD
7.如图,在△ABC中,AB=AC=5,BC=3,BD为中线,则△ABD与△BCD的周长之差为( )
A.1 B.2 C.3 D.4
8.如图,在中,已知点D、E、F分别为的中点,且,则阴影部分面积S是( )
A.1 B.2 C.3 D.4
二、填空题
9.在△ABC中,AB=6,BC=8,则AC的长x的取值范围是 。
10.如图,工人师傅在安装木制门框时,为防止变形常常钉上两根木条,这样做的依据是 .
11.一个三角形的两边长分别是3和7,且第三边长为奇数,这个三角形的最大周长是 ,
12.在中,AB=a,BC=b,的高AD与高CE的比是
13.如图,点D是中AB边上的点,点E是CD的中点,连接AE、BE,若的面积为8,则阴影部分的面积为 .
三、解答题
14.已知:a,b,c是三角形的三条边,化简:.
15.一个三角形的三边长分别是xcm、(x+2)cm、(x+5)cm.它的周长不超过37cm.求x的取值范围.
16.如图,在ABC中,AD是ABC的高,AE、BF是ABC角平分线,AE与BF相交于点O,∠BOA=125°,求∠DAC的度数.
17.已知△ABC的周长为33cm,AD是BC边上的中线,.
(1)如图,当AC=10cm时,求BD的长.
(2)若AC=12cm,能否求出DC的长?为什么?
18.如图,在中,,.于点E,平分.
(1)求证;
(2)求的度数.
参考答案
1.B
2.C
3.B
4.D
5.B
6.B
7.B
8.B
9.2<x<14
10.三角形具有稳定性
11.19
12.
13.4
14.解:∵a、b、c是三角形的三边长,
∴a-b-c<0,-a+b-c<0,a-c+b>0,
∴
=
=
=
15.解:∵一个三角形的三边长分别是xcm,(x+2)cm,(x+5)cm,它的周长不超过37cm,
∴ ,
解得:3<x≤10.
16.解:∵∠OAB+∠OBA+∠AOB=180°,∠AOB=125°,
∴∠OAB+∠OBA=180°﹣125°=55°,
∵AE、BF是△ABC角平分线,
∴∠OAB=∠BAC,∠OBA=∠ABC,
∴∠BAC+∠ABC=55°,
∴∠BAC+∠ABC=110°,
∵∠BAC+∠ABC+∠ACB=180°,
∴∠ACB=70°,
∵AD是△ABC的高,
∴∠ADC=90°,
∴∠DAC=90°﹣70°=20°.
17.(1)解:∵,AC=10cm,
∴AB=15cm.
又∵△ABC的周长是33cm,即
∴
∵AD是BC边上的中线,
∴.
(2)解:不能,理由如下:
∵,AC=12cm,
∴AB=18cm.
又∵△ABC的周长是33cm,
∴BC=3cm.
∵AC+BC=15cm<AB=18cm,
∴不能构成三角形ABC,
∴不能求出DC的长.
18.(1)证明:∵,,
∴,
∵AD平分,
∴,
∴,
∴;
(2)解:∵,
∴,
∵,
∴,
∴,
即.
