2023-2024学年人教版八年级数学上册11.2与三角形有关的角 同步达标测试题(含解析)
文档属性
| 名称 | 2023-2024学年人教版八年级数学上册11.2与三角形有关的角 同步达标测试题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 531.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-04 07:50:34 | ||
图片预览

文档简介
2023-2024学年人教版八年级数学上册《11.2与三角形有关的角》同步达标测试题(附答案)
一、单选题(满分40分)
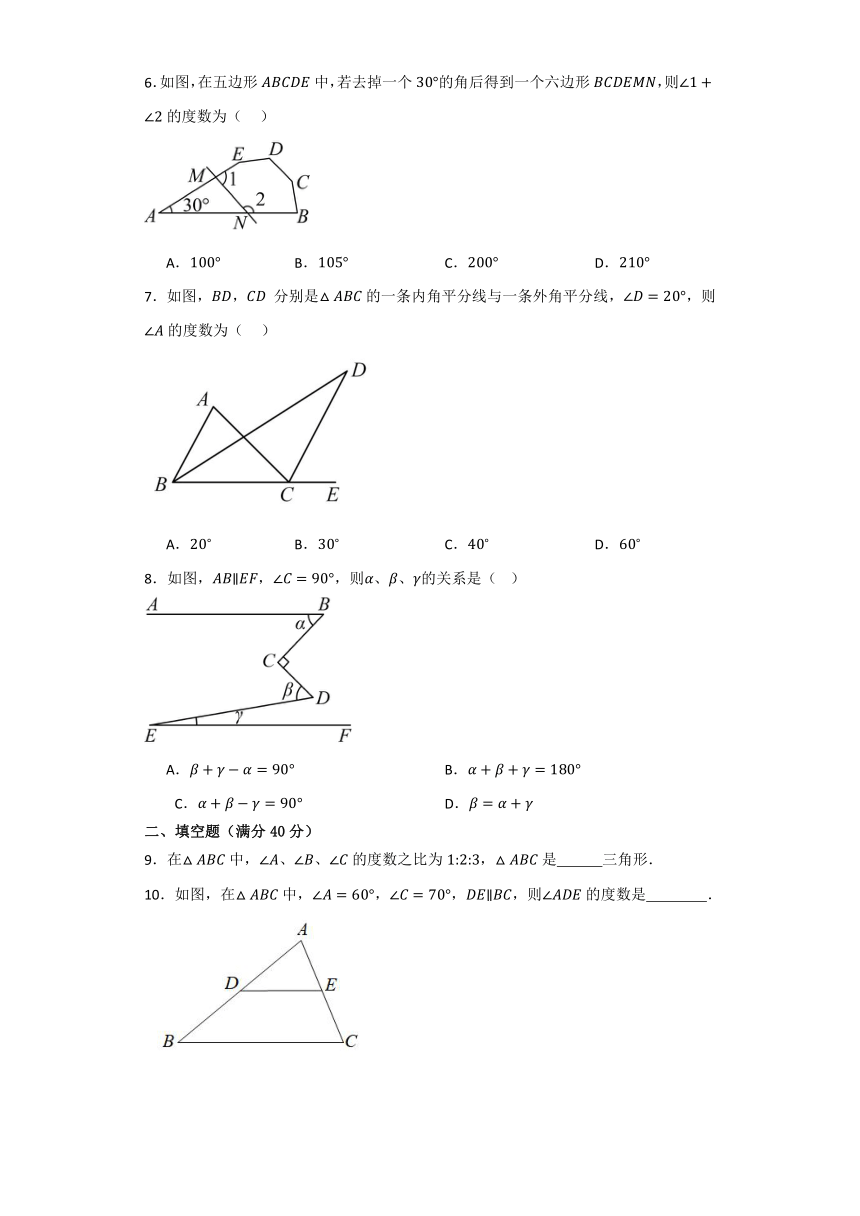
1.在中,,则的度数是( )
A. B. C. D.
2.如图,,则( )
A. B. C. D.
3.如图,中,与的平分线交于点,已知,则的度数是( )
A. B. C. D.
4.将一副三角板如图放置,使点在上,,则的度数为( )
A.45° B.50° C.60° D.75°
5.如图,在中,,,平分,于点E,则的度数为( )
A. B. C. D.
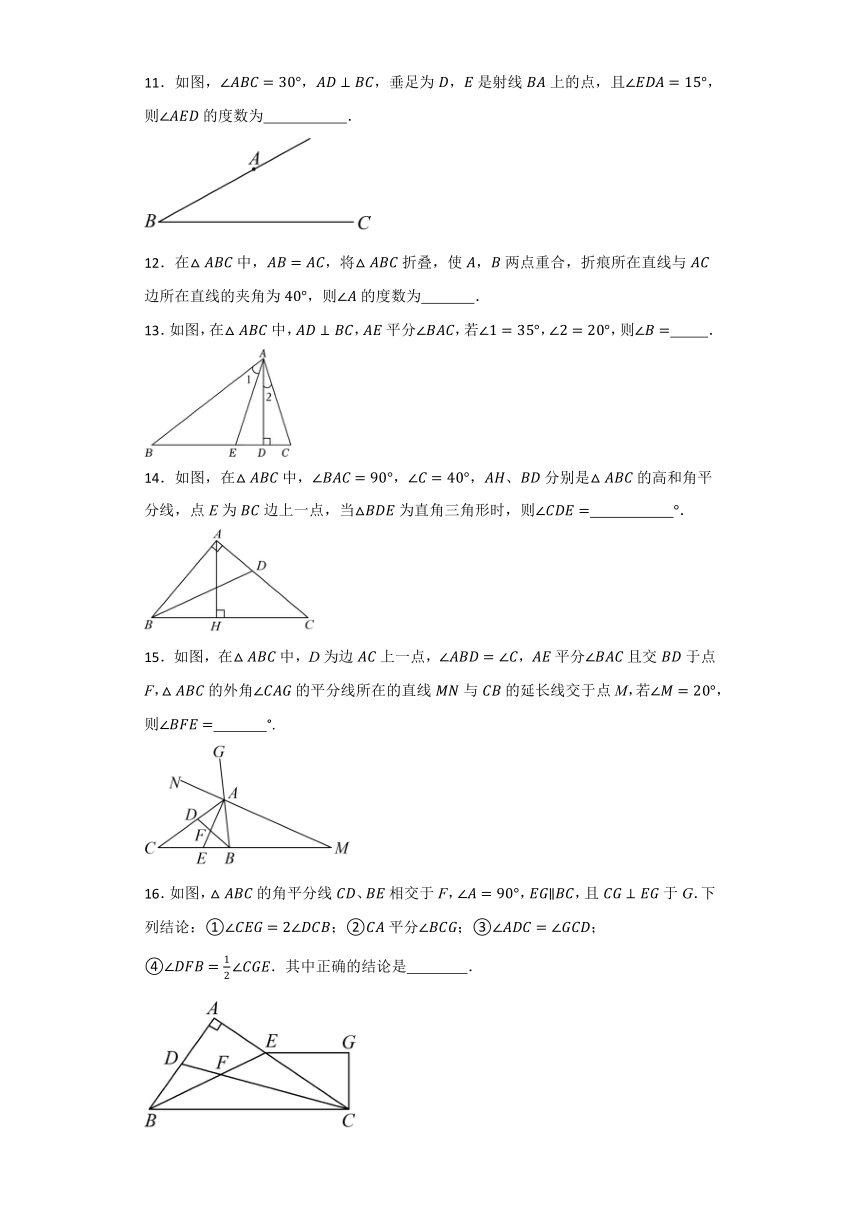
6.如图,在五边形中,若去掉一个的角后得到一个六边形,则的度数为( )
A. B. C. D.
7.如图,, 分别是的一条内角平分线与一条外角平分线,,则的度数为( )
A. B. C. D.
8.如图,,,则、、的关系是( )
B.
C. D.
二、填空题(满分40分)
9.在中,、、的度数之比为,是 三角形.
10.如图,在中,,,则的度数是 .
11.如图,,,垂足为,是射线上的点,且,则的度数为 .
12.在中,,将折叠,使,两点重合,折痕所在直线与边所在直线的夹角为,则的度数为 .
13.如图,在中,,平分,若,,则 .
14.如图,在中,,、分别是的高和角平分线,点E为边上一点,当为直角三角形时,则 .
15.如图,在中,D为边上一点,,平分且交于点F,的外角的平分线所在的直线与的延长线交于点M,若,则 °.
16.如图,的角平分线、相交于F,,,且于G.下列结论:①;②平分;③;④.其中正确的结论是 .
三、解答题(满分40分)
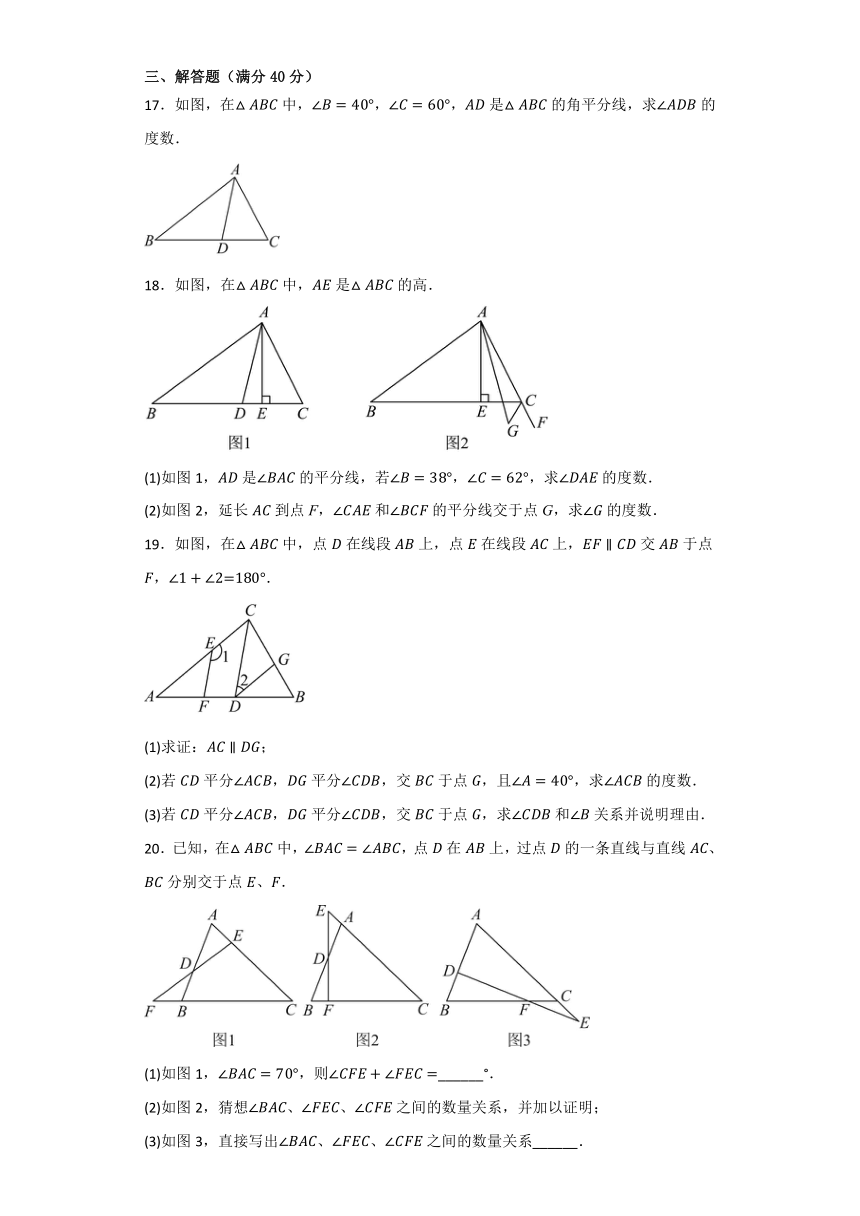
17.如图,在中,,,是的角平分线,求的度数.
18.如图,在中,是的高.
(1)如图1,是的平分线,若,求的度数.
(2)如图2,延长到点F,和的平分线交于点G,求的度数.
19.如图,在中,点在线段上,点在线段上,交于点,.
(1)求证:;
(2)若平分,平分,交于点,且,求的度数.
(3)若平分,平分,交于点,求和关系并说明理由.
20.已知,在中,,点在上,过点的一条直线与直线、分别交于点、.
(1)如图1,,则______°.
(2)如图2,猜想、、之间的数量关系,并加以证明;
(3)如图3,直接写出、、之间的数量关系______.
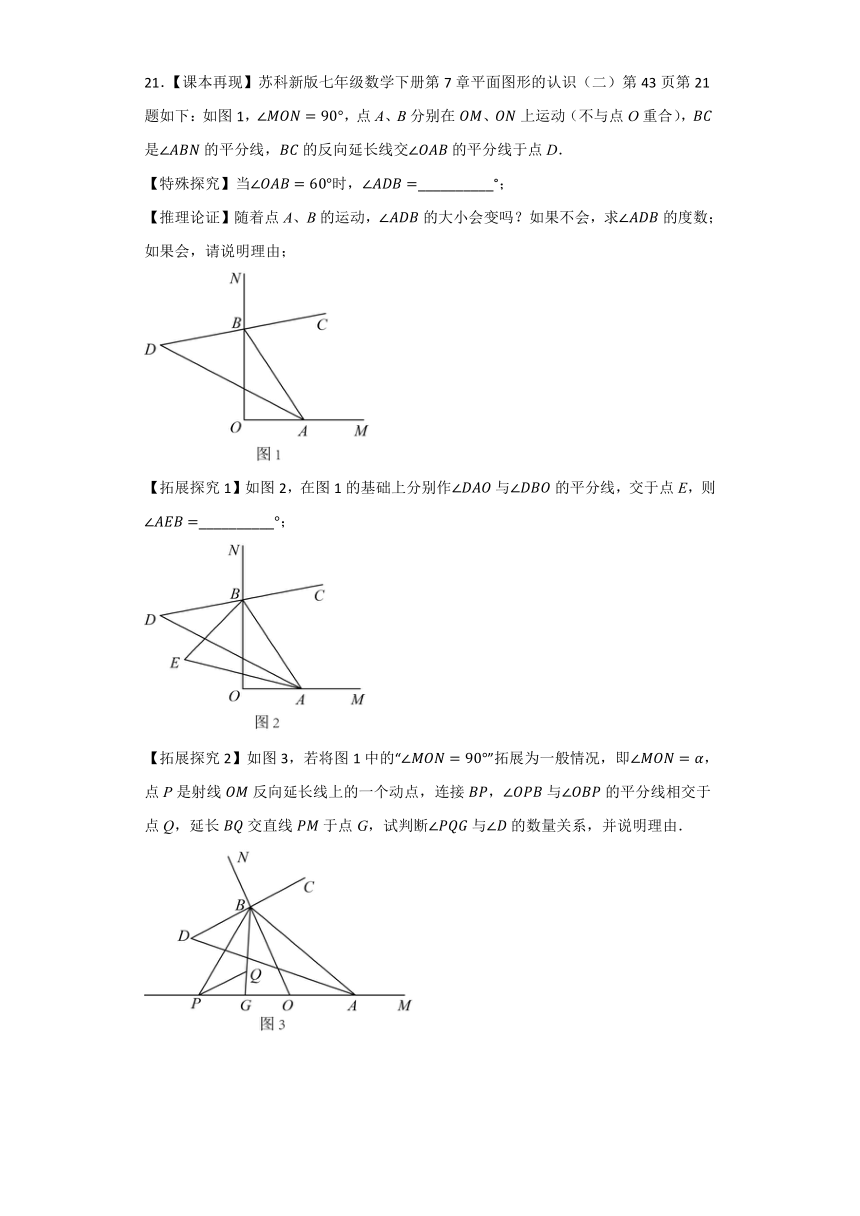
21.【课本再现】苏科新版七年级数学下册第7章平面图形的认识(二)第43页第21题如下:如图1,,点A、B分别在、上运动(不与点O重合),是的平分线,的反向延长线交的平分线于点D.
【特殊探究】当时,__________°;
【推理论证】随着点A、B的运动,的大小会变吗?如果不会,求的度数;如果会,请说明理由;
【拓展探究1】如图2,在图1的基础上分别作与的平分线,交于点E,则__________;
【拓展探究2】如图3,若将图1中的“”拓展为一般情况,即,点P是射线反向延长线上的一个动点,连接,与的平分线相交于点Q,延长交直线于点G,试判断与的数量关系,并说明理由.
参考答案
1.解:∵,
∴.
故选:C.
2.解:∵,
∴.
∵,
∴.
∴.
故选:A.
3.解:,
,
∵分别是的平分线,
,
,
.
故选:B.
4.解:∵,,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
故选D.
5.解:∵,
,
,
,
, 平分,
,
.
故选:C.
6.解:∵,
∴,
∵,
∴.
故选D.
7.解:∵平分,平分,
∴,,
∵是的外角,是的外角,
∴,,
∴,
化简,得,
∵,
,
故选:C.
8.解:延长交于,延长交于,如图,
,
在直角中,;
在中,,
,
,
,
;
故选:C.
9.解:设三个角的度数分别为,,,则
,
解得,,
,.
即该三角形的三个内角分别为,,,因而是直角三角形.
故答案为:直角.
10.解:在中,,
∴,
∵,
∴;
故答案为:.
11.解:如图所示,
∵,
∴
当在上时,,
当在的延长线上时,,
故答案为:或.
12.解:如图1,
由折叠的性质可知,
,
折痕所在直线与边所在直线的夹角为,
,
;
如图2,
由折叠的性质可知,
,
折痕所在直线与边所在直线的夹角为,
,
,
,
故答案为:或.
13.解:∵平分,
∴,
∴,
∵,
∴,
∴.
故答案为:.
14.解:∵,
∴
∵平分
∴
当为直角三角形时,有以下两种情况:
①当时,如图1,
∵,
∴;
②当时,如图2,
∴,
∵,
∴,
综上,的度数为或.
故答案为:50或25.
15.解:∵平分,平分,
∴,,
∵,
∴,
∴,
∵,
∴,
∵,,
∴,
∵,
∴.
故答案为:70.
16.解:①∵,
,
又是的角平分线,
,故①正确;
②无法证明平分,故②错误;
③,
,
平分,
,
.
∵,且,
,即,
,故③正确;
④,,
,
,
,故④正确.
故答案为:①③④.
17.解:在中,
,,
,
是的角平分线,
,
.
18.(1)解: ∵,
∴,
∵是的平分线,
∴,
∵是的高,
∴,
∵,
∴,
∴.
故的度数为.
(2)∵和的平分线交于点G,
∴,
∵
∴
∴
∵是的高,
∴
∴.
∴的度数为.
19.(1)证明:,
,
,
,
;
(2)解:,,
,,
平分,
,
,
平分,
;
(3)解:,
理由如下:
平分,平分,
,,
,
,
,
在中,,
,
.
20.(1)解:∵,,
∴,
∵,
∴,
∵,
∴;
(2),
证明:在中
∵,
∴,
在中,
∵,
∴,
∴,
∵,
∴;
(3)解:∵,,,
∴,
∴.
21.解:特殊探究:
,,是的平分线,的反向延长线交的平分线于点D,
,,
,,
,
,
故答案为:
推理论证:
设,
,是的平分线,的反向延长线交的平分线于点D,
,,,
,
,
拓展探究1:
设,
,是的平分线,的反向延长线交的平分线于点D,
,,,
,
在图1的基础上分别作与的平分线,交于点E,
,
,,
,
,
故答案为:
拓展探究2:
设,,
,是的平分线,的反向延长线交的平分线于点D,与的平分线相交于点Q,延长交直线于点G,
,,
,,
,
,
,,
,
,
,
,
一、单选题(满分40分)
1.在中,,则的度数是( )
A. B. C. D.
2.如图,,则( )
A. B. C. D.
3.如图,中,与的平分线交于点,已知,则的度数是( )
A. B. C. D.
4.将一副三角板如图放置,使点在上,,则的度数为( )
A.45° B.50° C.60° D.75°
5.如图,在中,,,平分,于点E,则的度数为( )
A. B. C. D.
6.如图,在五边形中,若去掉一个的角后得到一个六边形,则的度数为( )
A. B. C. D.
7.如图,, 分别是的一条内角平分线与一条外角平分线,,则的度数为( )
A. B. C. D.
8.如图,,,则、、的关系是( )
B.
C. D.
二、填空题(满分40分)
9.在中,、、的度数之比为,是 三角形.
10.如图,在中,,,则的度数是 .
11.如图,,,垂足为,是射线上的点,且,则的度数为 .
12.在中,,将折叠,使,两点重合,折痕所在直线与边所在直线的夹角为,则的度数为 .
13.如图,在中,,平分,若,,则 .
14.如图,在中,,、分别是的高和角平分线,点E为边上一点,当为直角三角形时,则 .
15.如图,在中,D为边上一点,,平分且交于点F,的外角的平分线所在的直线与的延长线交于点M,若,则 °.
16.如图,的角平分线、相交于F,,,且于G.下列结论:①;②平分;③;④.其中正确的结论是 .
三、解答题(满分40分)
17.如图,在中,,,是的角平分线,求的度数.
18.如图,在中,是的高.
(1)如图1,是的平分线,若,求的度数.
(2)如图2,延长到点F,和的平分线交于点G,求的度数.
19.如图,在中,点在线段上,点在线段上,交于点,.
(1)求证:;
(2)若平分,平分,交于点,且,求的度数.
(3)若平分,平分,交于点,求和关系并说明理由.
20.已知,在中,,点在上,过点的一条直线与直线、分别交于点、.
(1)如图1,,则______°.
(2)如图2,猜想、、之间的数量关系,并加以证明;
(3)如图3,直接写出、、之间的数量关系______.
21.【课本再现】苏科新版七年级数学下册第7章平面图形的认识(二)第43页第21题如下:如图1,,点A、B分别在、上运动(不与点O重合),是的平分线,的反向延长线交的平分线于点D.
【特殊探究】当时,__________°;
【推理论证】随着点A、B的运动,的大小会变吗?如果不会,求的度数;如果会,请说明理由;
【拓展探究1】如图2,在图1的基础上分别作与的平分线,交于点E,则__________;
【拓展探究2】如图3,若将图1中的“”拓展为一般情况,即,点P是射线反向延长线上的一个动点,连接,与的平分线相交于点Q,延长交直线于点G,试判断与的数量关系,并说明理由.
参考答案
1.解:∵,
∴.
故选:C.
2.解:∵,
∴.
∵,
∴.
∴.
故选:A.
3.解:,
,
∵分别是的平分线,
,
,
.
故选:B.
4.解:∵,,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
故选D.
5.解:∵,
,
,
,
, 平分,
,
.
故选:C.
6.解:∵,
∴,
∵,
∴.
故选D.
7.解:∵平分,平分,
∴,,
∵是的外角,是的外角,
∴,,
∴,
化简,得,
∵,
,
故选:C.
8.解:延长交于,延长交于,如图,
,
在直角中,;
在中,,
,
,
,
;
故选:C.
9.解:设三个角的度数分别为,,,则
,
解得,,
,.
即该三角形的三个内角分别为,,,因而是直角三角形.
故答案为:直角.
10.解:在中,,
∴,
∵,
∴;
故答案为:.
11.解:如图所示,
∵,
∴
当在上时,,
当在的延长线上时,,
故答案为:或.
12.解:如图1,
由折叠的性质可知,
,
折痕所在直线与边所在直线的夹角为,
,
;
如图2,
由折叠的性质可知,
,
折痕所在直线与边所在直线的夹角为,
,
,
,
故答案为:或.
13.解:∵平分,
∴,
∴,
∵,
∴,
∴.
故答案为:.
14.解:∵,
∴
∵平分
∴
当为直角三角形时,有以下两种情况:
①当时,如图1,
∵,
∴;
②当时,如图2,
∴,
∵,
∴,
综上,的度数为或.
故答案为:50或25.
15.解:∵平分,平分,
∴,,
∵,
∴,
∴,
∵,
∴,
∵,,
∴,
∵,
∴.
故答案为:70.
16.解:①∵,
,
又是的角平分线,
,故①正确;
②无法证明平分,故②错误;
③,
,
平分,
,
.
∵,且,
,即,
,故③正确;
④,,
,
,
,故④正确.
故答案为:①③④.
17.解:在中,
,,
,
是的角平分线,
,
.
18.(1)解: ∵,
∴,
∵是的平分线,
∴,
∵是的高,
∴,
∵,
∴,
∴.
故的度数为.
(2)∵和的平分线交于点G,
∴,
∵
∴
∴
∵是的高,
∴
∴.
∴的度数为.
19.(1)证明:,
,
,
,
;
(2)解:,,
,,
平分,
,
,
平分,
;
(3)解:,
理由如下:
平分,平分,
,,
,
,
,
在中,,
,
.
20.(1)解:∵,,
∴,
∵,
∴,
∵,
∴;
(2),
证明:在中
∵,
∴,
在中,
∵,
∴,
∴,
∵,
∴;
(3)解:∵,,,
∴,
∴.
21.解:特殊探究:
,,是的平分线,的反向延长线交的平分线于点D,
,,
,,
,
,
故答案为:
推理论证:
设,
,是的平分线,的反向延长线交的平分线于点D,
,,,
,
,
拓展探究1:
设,
,是的平分线,的反向延长线交的平分线于点D,
,,,
,
在图1的基础上分别作与的平分线,交于点E,
,
,,
,
,
故答案为:
拓展探究2:
设,,
,是的平分线,的反向延长线交的平分线于点D,与的平分线相交于点Q,延长交直线于点G,
,,
,,
,
,
,,
,
,
,
,
