2023-2024学年人教版八年级数学上册11.3多边形及其内角和 同步达标测试题(含解析)
文档属性
| 名称 | 2023-2024学年人教版八年级数学上册11.3多边形及其内角和 同步达标测试题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 413.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-04 07:53:21 | ||
图片预览




文档简介
2023-2024学年人教版八年级数学上册《11.3多边形及其内角和》
同步达标测试题(附答案)
一、单选题(满分40分)
1.若正多边形的内角和是,则该正多边形的一个外角是( )
A. B. C. D.
2.一个多边形的每一个外角都等于,则这个多边形的边数是( )
A. B. C. D.
3.如果一个多边形的内角和等于四边形的外角和的2倍,那么这个多边形是( )
A.四边形 B.五边形 C.六边形 D.七边形
4.用形状、大小完全相同的一种或几种平面图形进行拼接,彼此之间不留空隙、不重叠的铺成一片,就是平面图形的镶嵌.只用下面一种图形能够进行平面镶嵌的是( )
A.正三角形 B.正五边形 C.正八边形 D.正十二边形
5.若一个正多边形每一个内角的度数比它的每个外角的度数多,则这个多边形是( )
A.正八边形 B.正九边形 C.正十边形 D.正十一边形
6.从边形的一个顶点引出的对角线把它最多划分为个三角形,则的值为( )
A. B. C. D.
7.如图,七边形中,、的延长线交于点O,若、、、的外角和等于,则的度数为( )
A. B. C. D.
8.如图,将正五边形和长方形按如图方程叠放在一起,则的度数为( )
A. B. C. D.
二、填空题(满分40分)
9.一个多边形所有的内角与它所有的外角之和是,过这个多边形的一个顶点可画出 条对角线.
10.一个正多边形的内角和是它的外角和的两倍,则这个正多边形是正 边形.
11.如用边长相同的正三角形、正方形、正六边形、正八边形、正十边形进行密铺,每个交叉点只允许五块进行密铺,它有( )种铺法.
12.如图,四边形中,,,的平分线交于点E,过点E作.若,则的度数为 .
13.一个多边形从同一个顶点引出的对角线,将这个多边形分成5个三角形,则这个多边形的内角和是 °.
14.在中,,,将、按照如图所示折叠,若,则 °
15.如图所示,则的度数是 .
16.如图, °.
三、解答题(满分40分)
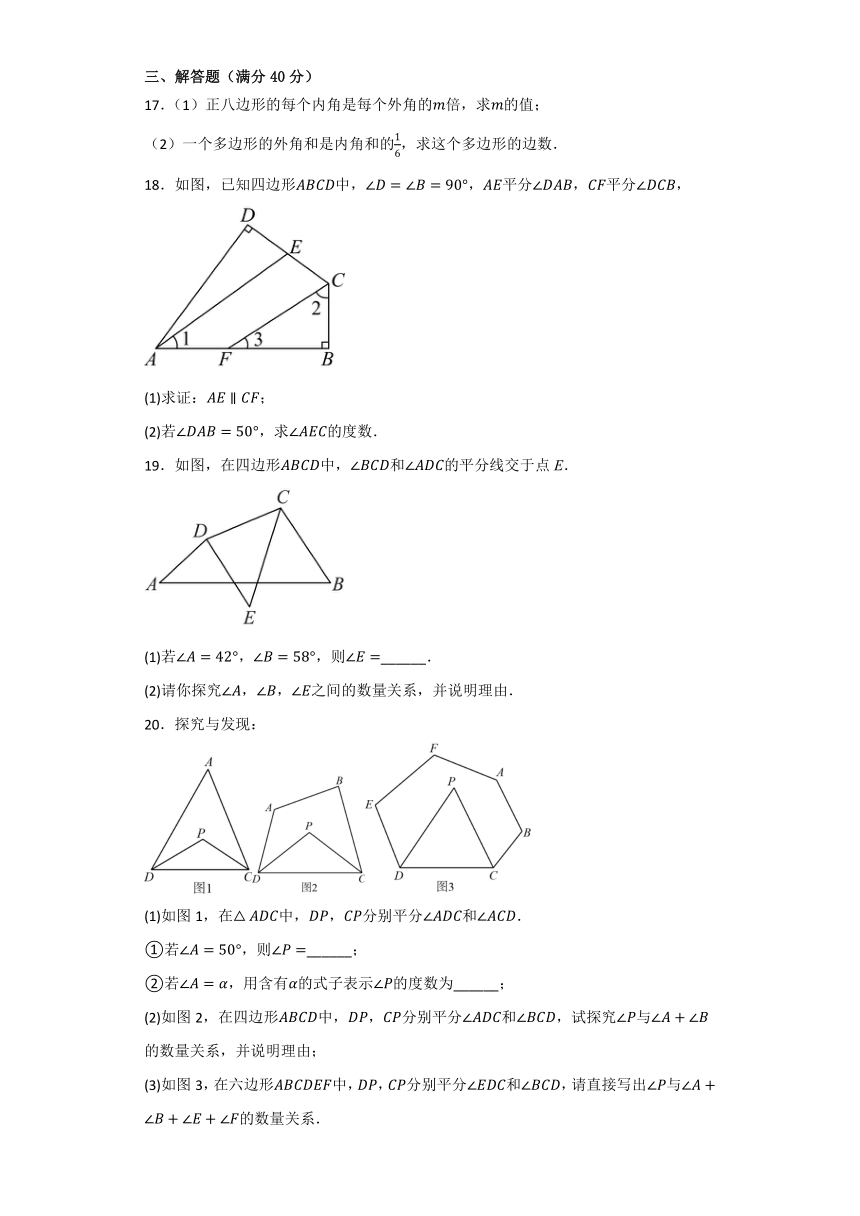
17.(1)正八边形的每个内角是每个外角的倍,求的值;
(2)一个多边形的外角和是内角和的,求这个多边形的边数.
18.如图,已知四边形中,平分平分,
(1)求证:;
(2)若,求的度数.
19.如图,在四边形中,和的平分线交于点E.
(1)若,,则______.
(2)请你探究,,之间的数量关系,并说明理由.
20.探究与发现:
(1)如图1,在中,,分别平分和.
①若,则______;
②若,用含有的式子表示的度数为______;
(2)如图2,在四边形中,,分别平分和,试探究与的数量关系,并说明理由;
(3)如图3,在六边形中,,分别平分和,请直接写出与的数量关系.
21.阅读:基本图形通常是指能够反映一个或几个定理,或者能够反映图形基本规律的几何图形.这些图形以基本概念、基本事实、定理、常用的数学结论和基本规律为基础,图形简单又具有代表性.在几何问题中,熟练把握和灵活构造基本图形,能更好地帮助我们解决问题.
我们将图1①所示的图形称为“8字形”.在这个“8字形”中,存在结论.
我们将图1②所示的凹四边形称为“飞镖形”.在这个“飞镖形”中,存在结论.
(1)直接利用上述基本图形中的任意一种,解决问题:
如图2,、分别平分、,说明:.
(2)将图2看作基本图形,直接利用(1)中的结论解决下列问题:
①如图3,直线平分的外角,平分的外角,若,,求的度数.
②在图4中,平分的外角,平分的外角,猜想与、的关系(直接写出结果,无需说明理由).
③在图5中,平分,平分的外角,猜想与、的关系(直接写出结果,无需说明理由).
参考答案
1.解:设此多边形为边形,
根据题意得:,
解得:,
这个正多边形的每一个外角等于:.
故选:B.
2.解:,
这个多边形的边数是,
故选:C.
3.解:设这个多边形边数是n,根据题意得:
,
解得:,
即这个多边形是六边形,故C正确.
故选:C.
4.解:A、正三角形的内角为
∴,是整数,故符合题意;
B、正五边形的内角为
∴,不是整数,故不符合题意;
C、正八边形的内角为
∴,不是整数,故不符合题意;
D、正十二边形的内角为
∴,不是整数,故不符合题意;
故选:A.
5.解:设这个正多边形每个内角为x,
根据题意得:,
解得:,
∴这个正多边形每个外角是,
则这个正多边形的边数;
故选:B.
6.解:依题意有,
解得:.
故选:D.
7.解:五边形的外角和为,且七边形中,,,,的外角和等于,
,
,
故选:C.
8.解:∵正五边形内角和为:,
∴,
∵长方形中,,
∴,
∴,
故选C.
9.解:根据题意,得
,
解得:.
那么过这个多边形的一个顶点可作条对角线.
故答案为:2.
10.解:设这个正多边形是正n边形,
则,
解得,
即这个正多边形是正六边形.
故答案为:六.
11.解:如果是一种图形的镶嵌,每个内角度数应是360÷5=72°,边数应是360÷(180-72)非整数,所以不存在;常见的两种图形的镶嵌有:正三角形和正方形;正三角形和正六边形;正方形和正八边形. 正三角形的每个内角是60°,正方形的每个内角是90°,∵3×60°+2×90°=360°,∴正三角形和正方形符合五块进行密铺; 正六边形的每个内角是120°,正三角形的每个内角是60度.∵2×120°+2×60°=360°,或120°+4×60°=360°,∴正三角形和正六边形符合五块进行密铺;正方形的每个内角是90°,正八边形的每个内角为:180°-360°÷8=135°,∵90°+2×135°=360°∴不符合五块进行密铺,三种图形的镶嵌,有1个正三角形和2个正四边形和1个正六边形,不符合五块进行密铺:1个正四边形和1个正六边形和1个正十二边形,不符合五块进行密铺,
3正三角形和正四边形和正十二边形,不符合五块进行密铺,四种图形的镶嵌,较小的四个内角的和已是405°,所以不存在,五种图形更不可能.综上,共有两种铺法.
12.解:,,
,
在四边形中,,,
,
,
,
故答案为:.
13.解:∵该多边形从同一顶点引出的对角线将多边形分为5个三角形,
∴该多变形为,七边形,
∵多边形内角和公式:,
∴七边形内角和为:,
故答案为:.
14.解:根据折叠性质得,,.
∵,,
∴,,
∴,,
∴.
在四边形中,.
∴,
即,
∴,
∴.
故答案为:265.
15.解:如图所示,与交于点,连接,
∴在中,,
在中,,
∴,
∵,,
∴,
∵四边形的内角和为,
∴,
故答案为:.
16.解:如图,
四边形的内角和为,
四边形中,,
四边形中,
∴
∴;
故答案为:.
17.解:(1)∵正八边形的每个内角,正八边形的每个外角,
∴;
(2)设这个多边形的边数为,根据题意得:,
解得.
∴这个多边形是十四边形.
18.(1)证明: 平分,
,
平分,
,
,
由四边形内角和为可知,
,
,
,
;
(2)解: ,平分,
,
在中,,,则,
.
19.(1)解:∵平分,平分,
∴,.
∵
∴
∴,
∴,
解得.
(2)解:.
理由:∵平分,平分,
∴,.
∵
∴
∴,
∴.
20.(1)解①,
.
,分别平分和,
,.
.
.
②,
.
,分别平分和,
,.
.
.
故答案为:①;②;
(2)解:,理由如下:
根据题意,得.
,分别平分和,
,.
.
;
(3)解:.
理由如下:
根据题意,得.
,分别平分和,
,.
.
∴
.
21.(1)解:∵分别平分,
∴,
∴,
由题干的结论得:,∠,
∴,
∴,
∴,即;
(2)解:①如图所示,分作的角平分线交于H,
由(1)的结论可知,
∵分别平分,
∴,
∵
∴,
∴,
同理可得,
由题干的结论可得,
∴;
②如图所示,分作的角平分线交于H,
由(1)的结论可知,,
同理可得,,
∴;
③由题干的结论可得,
∵平分,平分的外角,
∴,
∵,
∴,
由题干的结论可知,
∴,
∴
.
同步达标测试题(附答案)
一、单选题(满分40分)
1.若正多边形的内角和是,则该正多边形的一个外角是( )
A. B. C. D.
2.一个多边形的每一个外角都等于,则这个多边形的边数是( )
A. B. C. D.
3.如果一个多边形的内角和等于四边形的外角和的2倍,那么这个多边形是( )
A.四边形 B.五边形 C.六边形 D.七边形
4.用形状、大小完全相同的一种或几种平面图形进行拼接,彼此之间不留空隙、不重叠的铺成一片,就是平面图形的镶嵌.只用下面一种图形能够进行平面镶嵌的是( )
A.正三角形 B.正五边形 C.正八边形 D.正十二边形
5.若一个正多边形每一个内角的度数比它的每个外角的度数多,则这个多边形是( )
A.正八边形 B.正九边形 C.正十边形 D.正十一边形
6.从边形的一个顶点引出的对角线把它最多划分为个三角形,则的值为( )
A. B. C. D.
7.如图,七边形中,、的延长线交于点O,若、、、的外角和等于,则的度数为( )
A. B. C. D.
8.如图,将正五边形和长方形按如图方程叠放在一起,则的度数为( )
A. B. C. D.
二、填空题(满分40分)
9.一个多边形所有的内角与它所有的外角之和是,过这个多边形的一个顶点可画出 条对角线.
10.一个正多边形的内角和是它的外角和的两倍,则这个正多边形是正 边形.
11.如用边长相同的正三角形、正方形、正六边形、正八边形、正十边形进行密铺,每个交叉点只允许五块进行密铺,它有( )种铺法.
12.如图,四边形中,,,的平分线交于点E,过点E作.若,则的度数为 .
13.一个多边形从同一个顶点引出的对角线,将这个多边形分成5个三角形,则这个多边形的内角和是 °.
14.在中,,,将、按照如图所示折叠,若,则 °
15.如图所示,则的度数是 .
16.如图, °.
三、解答题(满分40分)
17.(1)正八边形的每个内角是每个外角的倍,求的值;
(2)一个多边形的外角和是内角和的,求这个多边形的边数.
18.如图,已知四边形中,平分平分,
(1)求证:;
(2)若,求的度数.
19.如图,在四边形中,和的平分线交于点E.
(1)若,,则______.
(2)请你探究,,之间的数量关系,并说明理由.
20.探究与发现:
(1)如图1,在中,,分别平分和.
①若,则______;
②若,用含有的式子表示的度数为______;
(2)如图2,在四边形中,,分别平分和,试探究与的数量关系,并说明理由;
(3)如图3,在六边形中,,分别平分和,请直接写出与的数量关系.
21.阅读:基本图形通常是指能够反映一个或几个定理,或者能够反映图形基本规律的几何图形.这些图形以基本概念、基本事实、定理、常用的数学结论和基本规律为基础,图形简单又具有代表性.在几何问题中,熟练把握和灵活构造基本图形,能更好地帮助我们解决问题.
我们将图1①所示的图形称为“8字形”.在这个“8字形”中,存在结论.
我们将图1②所示的凹四边形称为“飞镖形”.在这个“飞镖形”中,存在结论.
(1)直接利用上述基本图形中的任意一种,解决问题:
如图2,、分别平分、,说明:.
(2)将图2看作基本图形,直接利用(1)中的结论解决下列问题:
①如图3,直线平分的外角,平分的外角,若,,求的度数.
②在图4中,平分的外角,平分的外角,猜想与、的关系(直接写出结果,无需说明理由).
③在图5中,平分,平分的外角,猜想与、的关系(直接写出结果,无需说明理由).
参考答案
1.解:设此多边形为边形,
根据题意得:,
解得:,
这个正多边形的每一个外角等于:.
故选:B.
2.解:,
这个多边形的边数是,
故选:C.
3.解:设这个多边形边数是n,根据题意得:
,
解得:,
即这个多边形是六边形,故C正确.
故选:C.
4.解:A、正三角形的内角为
∴,是整数,故符合题意;
B、正五边形的内角为
∴,不是整数,故不符合题意;
C、正八边形的内角为
∴,不是整数,故不符合题意;
D、正十二边形的内角为
∴,不是整数,故不符合题意;
故选:A.
5.解:设这个正多边形每个内角为x,
根据题意得:,
解得:,
∴这个正多边形每个外角是,
则这个正多边形的边数;
故选:B.
6.解:依题意有,
解得:.
故选:D.
7.解:五边形的外角和为,且七边形中,,,,的外角和等于,
,
,
故选:C.
8.解:∵正五边形内角和为:,
∴,
∵长方形中,,
∴,
∴,
故选C.
9.解:根据题意,得
,
解得:.
那么过这个多边形的一个顶点可作条对角线.
故答案为:2.
10.解:设这个正多边形是正n边形,
则,
解得,
即这个正多边形是正六边形.
故答案为:六.
11.解:如果是一种图形的镶嵌,每个内角度数应是360÷5=72°,边数应是360÷(180-72)非整数,所以不存在;常见的两种图形的镶嵌有:正三角形和正方形;正三角形和正六边形;正方形和正八边形. 正三角形的每个内角是60°,正方形的每个内角是90°,∵3×60°+2×90°=360°,∴正三角形和正方形符合五块进行密铺; 正六边形的每个内角是120°,正三角形的每个内角是60度.∵2×120°+2×60°=360°,或120°+4×60°=360°,∴正三角形和正六边形符合五块进行密铺;正方形的每个内角是90°,正八边形的每个内角为:180°-360°÷8=135°,∵90°+2×135°=360°∴不符合五块进行密铺,三种图形的镶嵌,有1个正三角形和2个正四边形和1个正六边形,不符合五块进行密铺:1个正四边形和1个正六边形和1个正十二边形,不符合五块进行密铺,
3正三角形和正四边形和正十二边形,不符合五块进行密铺,四种图形的镶嵌,较小的四个内角的和已是405°,所以不存在,五种图形更不可能.综上,共有两种铺法.
12.解:,,
,
在四边形中,,,
,
,
,
故答案为:.
13.解:∵该多边形从同一顶点引出的对角线将多边形分为5个三角形,
∴该多变形为,七边形,
∵多边形内角和公式:,
∴七边形内角和为:,
故答案为:.
14.解:根据折叠性质得,,.
∵,,
∴,,
∴,,
∴.
在四边形中,.
∴,
即,
∴,
∴.
故答案为:265.
15.解:如图所示,与交于点,连接,
∴在中,,
在中,,
∴,
∵,,
∴,
∵四边形的内角和为,
∴,
故答案为:.
16.解:如图,
四边形的内角和为,
四边形中,,
四边形中,
∴
∴;
故答案为:.
17.解:(1)∵正八边形的每个内角,正八边形的每个外角,
∴;
(2)设这个多边形的边数为,根据题意得:,
解得.
∴这个多边形是十四边形.
18.(1)证明: 平分,
,
平分,
,
,
由四边形内角和为可知,
,
,
,
;
(2)解: ,平分,
,
在中,,,则,
.
19.(1)解:∵平分,平分,
∴,.
∵
∴
∴,
∴,
解得.
(2)解:.
理由:∵平分,平分,
∴,.
∵
∴
∴,
∴.
20.(1)解①,
.
,分别平分和,
,.
.
.
②,
.
,分别平分和,
,.
.
.
故答案为:①;②;
(2)解:,理由如下:
根据题意,得.
,分别平分和,
,.
.
;
(3)解:.
理由如下:
根据题意,得.
,分别平分和,
,.
.
∴
.
21.(1)解:∵分别平分,
∴,
∴,
由题干的结论得:,∠,
∴,
∴,
∴,即;
(2)解:①如图所示,分作的角平分线交于H,
由(1)的结论可知,
∵分别平分,
∴,
∵
∴,
∴,
同理可得,
由题干的结论可得,
∴;
②如图所示,分作的角平分线交于H,
由(1)的结论可知,,
同理可得,,
∴;
③由题干的结论可得,
∵平分,平分的外角,
∴,
∵,
∴,
由题干的结论可知,
∴,
∴
.
