4.1几何图形 同步练习 2023-2024学年人教版数学七年级上册(含答案)
文档属性
| 名称 | 4.1几何图形 同步练习 2023-2024学年人教版数学七年级上册(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 63.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-04 00:00:00 | ||
图片预览

文档简介
4.1几何图形 同步练习 2023-2024学年人教版数学七年级上册
姓名 班级 学号 成绩
一、选择题:(本题共8小题,每小题5分,共40分.)
1.按组成面的平或曲划分,与圆柱为同一类的几何体是( )
A.长方体 B.正方体 C.棱柱 D.圆锥
2.如图所示,陀螺是由下面哪两个几何体组合而成的( )
A.长方体和圆锥 B.长方形和三角形
C.圆和三角形 D.圆柱和圆锥
3.如图,用一个平面去截正方体截面形状不可能为下图中的( )
A. B. C. D.
4.下面四个图形是多面体的展开图,其中哪一个是四棱锥的展开图( )
A. B. C. D.
5.小明用5个大小一样的正方形制成如图所示的拼接图形(阴影部分),若在图中只添加一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子,这样的拼接方式有( )
A.1种 B.2种 C.3种 D.4种
6.用一个平面去截一个几何体,截面形状为四边形,则这个几何体不可能为( )
A.正方体 B.圆柱 C.圆锥 D.三棱柱
7.一个正方体,六个面上分别写着六个连续的整数,且每个相对面上的两个数之和相等,如图,你能看到的数为 , , ,则六个整数的和为( )
A.51 B.52 C.57 D.63
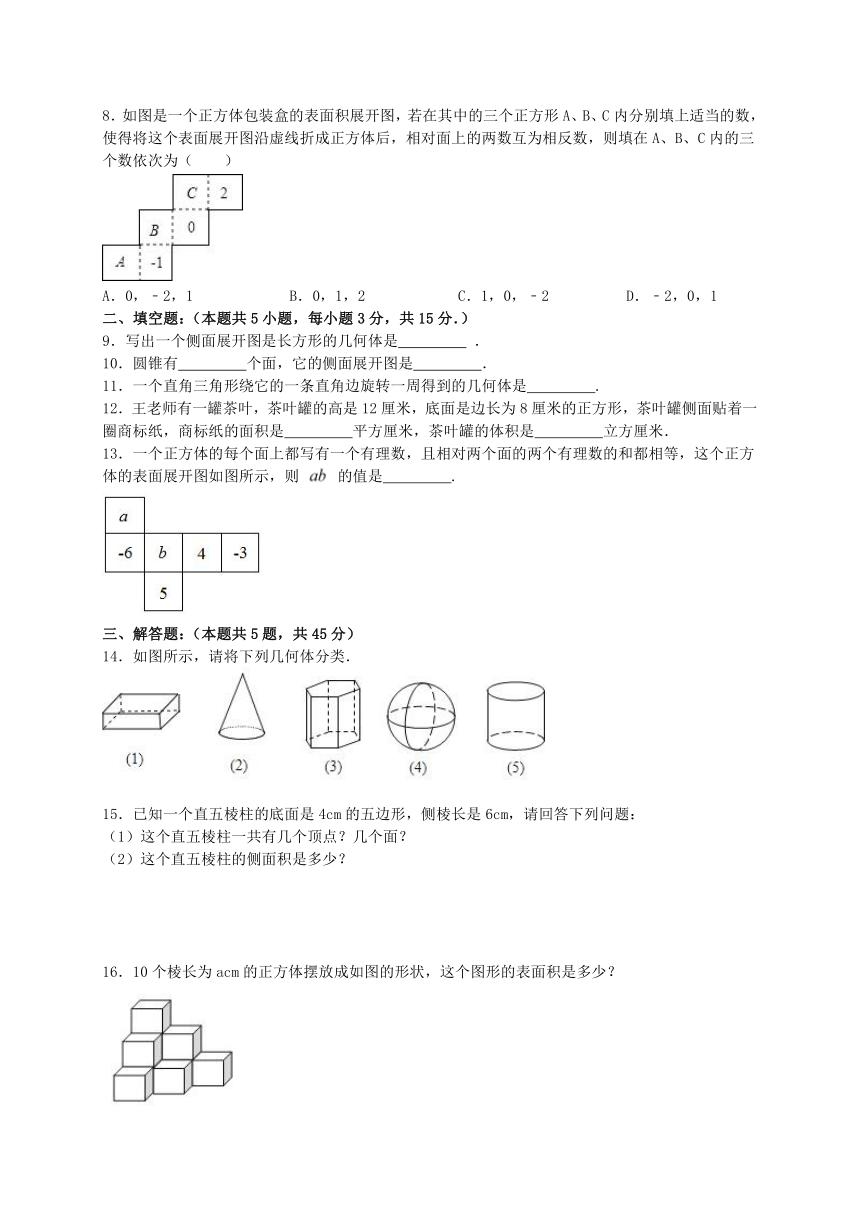
8.如图是一个正方体包装盒的表面积展开图,若在其中的三个正方形A、B、C内分别填上适当的数,使得将这个表面展开图沿虚线折成正方体后,相对面上的两数互为相反数,则填在A、B、C内的三个数依次为( )
A.0,﹣2,1 B.0,1,2 C.1,0,﹣2 D.﹣2,0,1
二、填空题:(本题共5小题,每小题3分,共15分.)
9.写出一个侧面展开图是长方形的几何体是 .
10.圆锥有 个面,它的侧面展开图是 .
11.一个直角三角形绕它的一条直角边旋转一周得到的几何体是 .
12.王老师有一罐茶叶,茶叶罐的高是12厘米,底面是边长为8厘米的正方形,茶叶罐侧面贴着一圈商标纸,商标纸的面积是 平方厘米,茶叶罐的体积是 立方厘米.
13.一个正方体的每个面上都写有一个有理数,且相对两个面的两个有理数的和都相等,这个正方体的表面展开图如图所示,则 的值是 .
三、解答题:(本题共5题,共45分)
14.如图所示,请将下列几何体分类.
15.已知一个直五棱柱的底面是4cm的五边形,侧棱长是6cm,请回答下列问题:
(1)这个直五棱柱一共有几个顶点?几个面?
(2)这个直五棱柱的侧面积是多少?
16.10个棱长为acm的正方体摆放成如图的形状,这个图形的表面积是多少?
17.如图所示,已知直角三角形纸板ABC,直角边AB=4 cm,BC=8 cm.
(1)将直角三角形纸板ABC绕三角形的边所在的直线旋转一周,能得到 种不同的几何体;(2)分别计算绕三角形直角边所在的直线旋转一周,得到几何体的体积.(取3)
18.如图是一个长方体的展开图,每个面上都标注了字母,请根据要求回答问题:
(1)如果A面在长方体的底部,那么哪一个面会在上面
(2)如果F面在前面,B面在左面,那么哪一个面会在上面 (字母朝外)
参考答案:
1.D 2.D 3.A 4.C 5.C 6.C 7.A 8.A
9.正方体
10.二;扇形
11.圆锥
12.384;768
13.-7
14.解:方法一:(1)、(3)、(5)是一类,都是柱体;(2)是锥体;(4)是球体.
方法二:(1)、(3)是一类,全是由平面构成的;(2)、(5)是一类,既有平面,又有曲面;(4)是一类,只有曲面.
15.(1)有10个顶点,7个面
(2)侧面积是120cm2
解析:解答:(1)这个直五棱柱一共有10个顶点,7个面;(2)4×6×5=120(cm2).
分析:(1)根据直五棱柱的特征解答;(2)求出直五棱柱1个侧面的面积,再乘以5即可得到这个直五棱柱的侧面积.
16.解:6×6×(a×a)=36a2(cm2)
故这个图形的表面积是36a2cm2.
17.(1)3
(2)解:①当绕三角形直角边AB所在的直线旋转一周时,得到几何体的体积为 ×π×82×4=256(cm3);②当绕三角形直角边BC所在的直线旋转一周时,得到几何体的体积为
×π×42×8=128(cm3).
18.(1)解:由图可知,“A”与“F”相对,“B”与“D”相对,则“C”与“E”相对.
因为面“A”与面“F”相对,所以A面是长方体的底部时,F面在上面.
(2)解:由图可知,如果F面在前面,B面在左面,那么“E”面在下面,因为“C”与 “E”相对,所以C面会在上面
姓名 班级 学号 成绩
一、选择题:(本题共8小题,每小题5分,共40分.)
1.按组成面的平或曲划分,与圆柱为同一类的几何体是( )
A.长方体 B.正方体 C.棱柱 D.圆锥
2.如图所示,陀螺是由下面哪两个几何体组合而成的( )
A.长方体和圆锥 B.长方形和三角形
C.圆和三角形 D.圆柱和圆锥
3.如图,用一个平面去截正方体截面形状不可能为下图中的( )
A. B. C. D.
4.下面四个图形是多面体的展开图,其中哪一个是四棱锥的展开图( )
A. B. C. D.
5.小明用5个大小一样的正方形制成如图所示的拼接图形(阴影部分),若在图中只添加一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子,这样的拼接方式有( )
A.1种 B.2种 C.3种 D.4种
6.用一个平面去截一个几何体,截面形状为四边形,则这个几何体不可能为( )
A.正方体 B.圆柱 C.圆锥 D.三棱柱
7.一个正方体,六个面上分别写着六个连续的整数,且每个相对面上的两个数之和相等,如图,你能看到的数为 , , ,则六个整数的和为( )
A.51 B.52 C.57 D.63
8.如图是一个正方体包装盒的表面积展开图,若在其中的三个正方形A、B、C内分别填上适当的数,使得将这个表面展开图沿虚线折成正方体后,相对面上的两数互为相反数,则填在A、B、C内的三个数依次为( )
A.0,﹣2,1 B.0,1,2 C.1,0,﹣2 D.﹣2,0,1
二、填空题:(本题共5小题,每小题3分,共15分.)
9.写出一个侧面展开图是长方形的几何体是 .
10.圆锥有 个面,它的侧面展开图是 .
11.一个直角三角形绕它的一条直角边旋转一周得到的几何体是 .
12.王老师有一罐茶叶,茶叶罐的高是12厘米,底面是边长为8厘米的正方形,茶叶罐侧面贴着一圈商标纸,商标纸的面积是 平方厘米,茶叶罐的体积是 立方厘米.
13.一个正方体的每个面上都写有一个有理数,且相对两个面的两个有理数的和都相等,这个正方体的表面展开图如图所示,则 的值是 .
三、解答题:(本题共5题,共45分)
14.如图所示,请将下列几何体分类.
15.已知一个直五棱柱的底面是4cm的五边形,侧棱长是6cm,请回答下列问题:
(1)这个直五棱柱一共有几个顶点?几个面?
(2)这个直五棱柱的侧面积是多少?
16.10个棱长为acm的正方体摆放成如图的形状,这个图形的表面积是多少?
17.如图所示,已知直角三角形纸板ABC,直角边AB=4 cm,BC=8 cm.
(1)将直角三角形纸板ABC绕三角形的边所在的直线旋转一周,能得到 种不同的几何体;(2)分别计算绕三角形直角边所在的直线旋转一周,得到几何体的体积.(取3)
18.如图是一个长方体的展开图,每个面上都标注了字母,请根据要求回答问题:
(1)如果A面在长方体的底部,那么哪一个面会在上面
(2)如果F面在前面,B面在左面,那么哪一个面会在上面 (字母朝外)
参考答案:
1.D 2.D 3.A 4.C 5.C 6.C 7.A 8.A
9.正方体
10.二;扇形
11.圆锥
12.384;768
13.-7
14.解:方法一:(1)、(3)、(5)是一类,都是柱体;(2)是锥体;(4)是球体.
方法二:(1)、(3)是一类,全是由平面构成的;(2)、(5)是一类,既有平面,又有曲面;(4)是一类,只有曲面.
15.(1)有10个顶点,7个面
(2)侧面积是120cm2
解析:解答:(1)这个直五棱柱一共有10个顶点,7个面;(2)4×6×5=120(cm2).
分析:(1)根据直五棱柱的特征解答;(2)求出直五棱柱1个侧面的面积,再乘以5即可得到这个直五棱柱的侧面积.
16.解:6×6×(a×a)=36a2(cm2)
故这个图形的表面积是36a2cm2.
17.(1)3
(2)解:①当绕三角形直角边AB所在的直线旋转一周时,得到几何体的体积为 ×π×82×4=256(cm3);②当绕三角形直角边BC所在的直线旋转一周时,得到几何体的体积为
×π×42×8=128(cm3).
18.(1)解:由图可知,“A”与“F”相对,“B”与“D”相对,则“C”与“E”相对.
因为面“A”与面“F”相对,所以A面是长方体的底部时,F面在上面.
(2)解:由图可知,如果F面在前面,B面在左面,那么“E”面在下面,因为“C”与 “E”相对,所以C面会在上面
