14.2 勾股定理的应用[上学期]
图片预览




文档简介
课件21张PPT。14.2 勾股定理的应用八年级数学(上册)? 华师大版学习目标1.知识与技能:牢固掌握勾股定理及其逆定理,并能利用它们
解决简单的实际问题2.过程与方法:通过解决实际问题,体会数学来源于生活,又
应用于生活,并学会如何将数学知识应用于实
际生活如何选择适当的数学模型解决数学问题。
3.情感态度与价值观:敢于面对数学学习中的困难,增加遇
到困难时选择其它方法的经验,进一步体会数
学的应用价值,形成积极参与数学活动的意识。
4.重点与难点:重点:勾股定理及其逆定理的实际应用。
难点:如何将实际问题中的“数”转化为定理中
的“形”,再转化为“数”。
解题关键理解题意,并画出符合条件的图形。
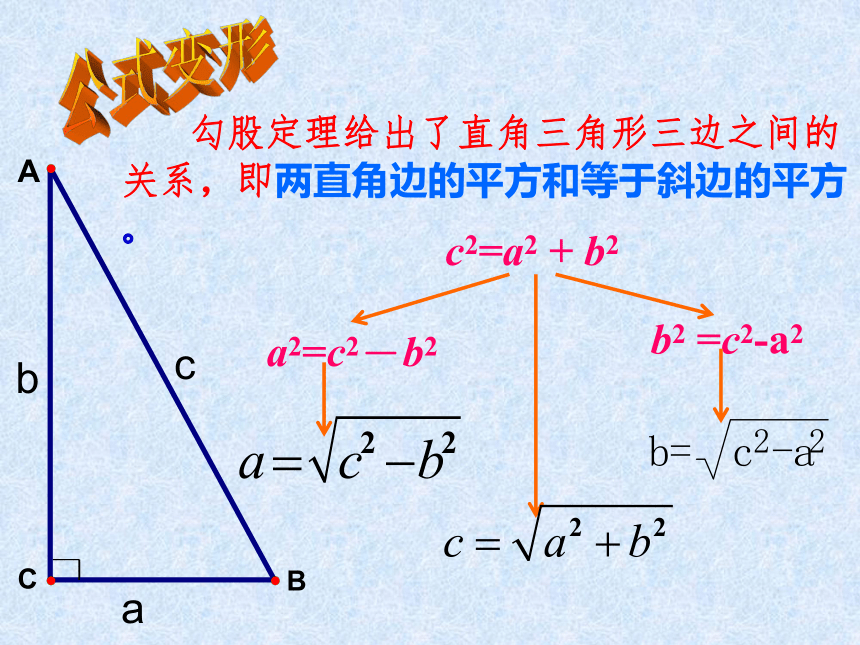
知识回顾勾股定理(毕达哥拉斯定理)(gou-gu theorem)如果直角三角形两直角边分别为a、b,斜边为c,那么即 直角三角形两直角边的平方和等于斜边的平方。 勾股定理给出了直角三角形三边之间的关系,即两直角边的平方和等于斜边的平方。cbac2=a2 + b2a2=c2-b2b2 =c2-a2公式变形勾股定理:如果直角三角形两直角边分别为a,b,斜边为c,那么 。a2 + b2 = c2互逆1、已知: Rt⊿ ABC
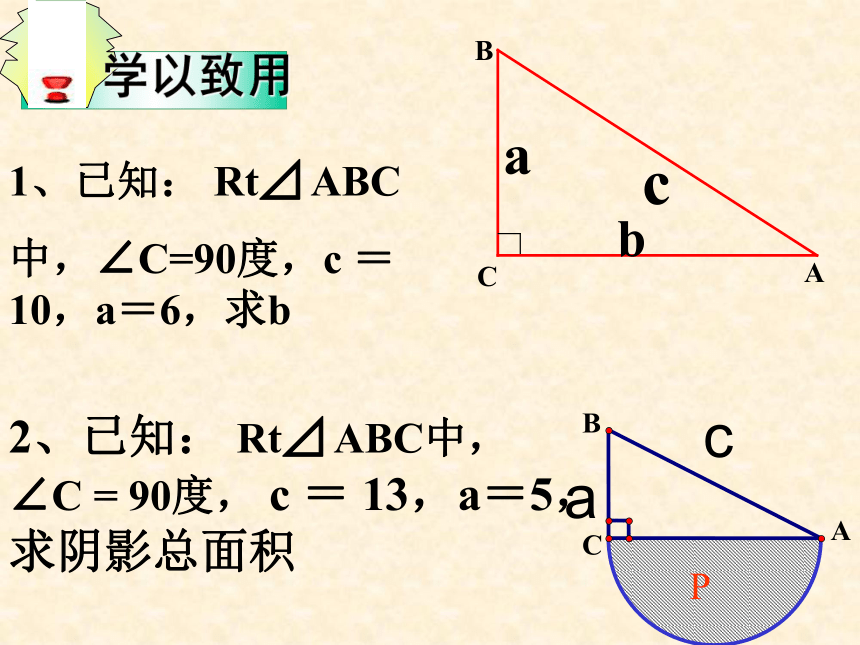
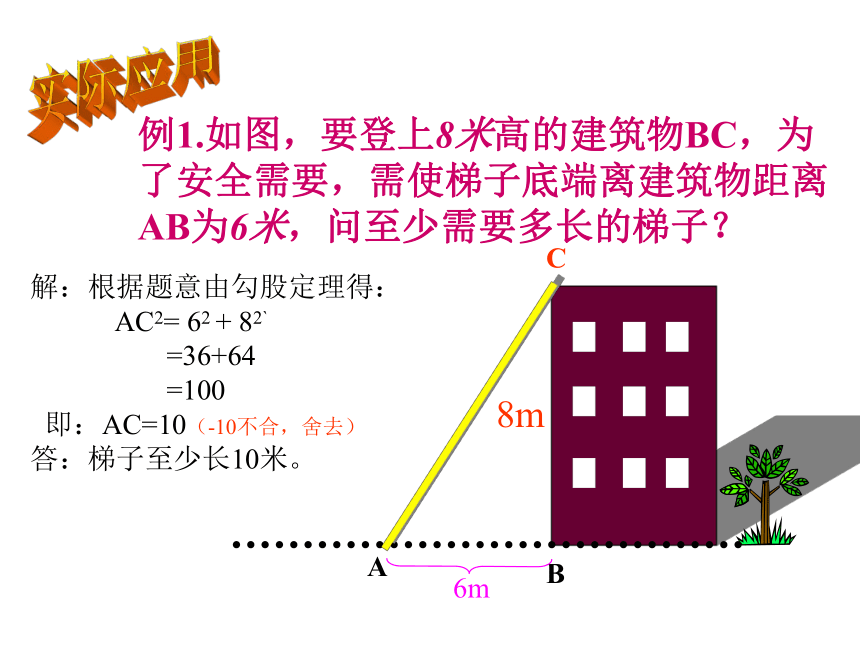
中,∠C=90度,c =10,a=6,求bABCABCP例1.如图,要登上8米高的建筑物BC,为了安全需要,需使梯子底端离建筑物距离AB为6米,问至少需要多长的梯子?
8mBCA6m解:根据题意由勾股定理得:
AC2= 62 + 82`
=36+64
=100
即:AC=10(-10不合,舍去)
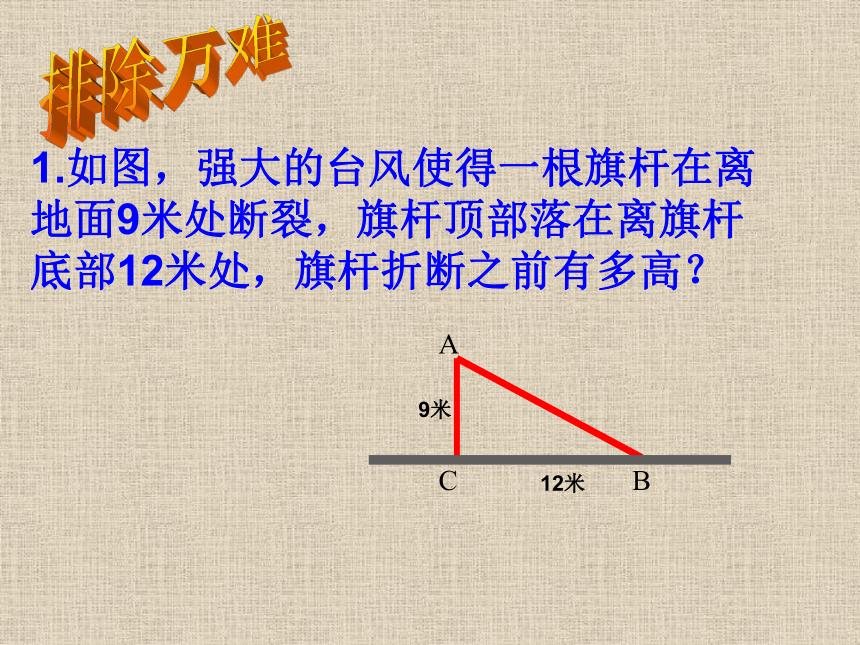
答:梯子至少长10米。实际应用1.如图,强大的台风使得一根旗杆在离地面9米处断裂,旗杆顶部落在离旗杆底部12米处,旗杆折断之前有多高?排除万难ABC 例2.甲乙两位探险者到沙漠进行探险,某日早晨
行走,上午10:00时,求甲乙两人的距离。1小时后,乙出发,以5千米/小时的速度向北
8:00甲先出发,以6千米/小时的速度向东行走,AOB分析:由题意可得:在⊿AOB中,∠AOB等于90度,OB表示甲走的路程,OA表示乙走的路程,AB表示10点时甲乙两人的距离。解:在Rt⊿AOB中,OA=OB=所以由勾股定理可得:答:甲乙两人的距离为13千米 学校组织野外考察活动.目的是测量一个小湖泊的最宽处有多少米?活动要求:
1.团队合作,设计出可行的测量方案。
2.找出需要测量计算所必须的数据。实地考察1.构造一个直角三角形ABC。2.测量出AC,BC的距离。3.利用勾股定理计算出AB的距离。参考方案:例3.葭生池中 今有方池一丈, 葭生其中央, 出水一尺, 引葭赴岸, 适与岸齐。 问:水深、葭长各几何? X-1X1尺解:可设葭长为x尺,则水深为(x-1)尺则有: (x-1)2+52=x2解得: x=13所以:葭长13尺,水深12尺。葭(jiá) 牛刀小试:印度有一数学家婆什迦罗曾提出过“荷花问题”:“平平湖水清可鉴, 面上半尺生红莲;
出泥不染亭亭立, 忽被强风吹一边。
渔人观看忙向前, 花离原位二尺远;
能算诸君请解题, 湖水如何知深浅?”“平平湖水清可鉴, 面上半尺生红莲; 出泥不染亭亭立, 忽被强风吹一边。
渔人观看忙向前, 花离原位二尺远;能算诸君请解题, 湖水如何知深浅?”分析:先把实际问题转化成数学问题。求:AB的长。根据勾股定理得: 解得 x = 3.75 (尺)答:湖水深3.75尺。解:设AB= x,则BD = x + 0.5,所以BC = BD = x + 0.5,在Rt△ABC中,∠BAC = 90o ,所以有:( x + 0.5 )2 = x2 + 22求:AB的长。12C例4.已知:四边形ABCD中,∠B=900,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积?3413名题鉴赏葛藤是自然界中一种聪明的植物,它自己腰杆不硬,为了享
受更多的阳光雨露,常常绕着树干盘旋而上,它还有一手绝
招,就是它绕树盘升的路线,总是沿最短路线螺旋前进!难
道植物也懂数学?通过阅读以上信息,你能设计一种方法解决下列问题吗?如果树的周长为3cm,绕一圈升高4cm,则它爬行的路线是什么?课时小结 谈谈你这节课的收获有哪些?
①会用勾股定理解决简单应用题.
②学会构造直角三角形.
③从生活中发现数学的奥妙.作业设计1、P58练习1、22、60页习题第2、6题课后探索 做一个长,宽,高分别为50厘米,40厘米,30厘米的木箱,一根长为70厘米的木棒能否放入,为什么?试用今天学过的知识说明。谢谢指导!
解决简单的实际问题2.过程与方法:通过解决实际问题,体会数学来源于生活,又
应用于生活,并学会如何将数学知识应用于实
际生活如何选择适当的数学模型解决数学问题。
3.情感态度与价值观:敢于面对数学学习中的困难,增加遇
到困难时选择其它方法的经验,进一步体会数
学的应用价值,形成积极参与数学活动的意识。
4.重点与难点:重点:勾股定理及其逆定理的实际应用。
难点:如何将实际问题中的“数”转化为定理中
的“形”,再转化为“数”。
解题关键理解题意,并画出符合条件的图形。
知识回顾勾股定理(毕达哥拉斯定理)(gou-gu theorem)如果直角三角形两直角边分别为a、b,斜边为c,那么即 直角三角形两直角边的平方和等于斜边的平方。 勾股定理给出了直角三角形三边之间的关系,即两直角边的平方和等于斜边的平方。cbac2=a2 + b2a2=c2-b2b2 =c2-a2公式变形勾股定理:如果直角三角形两直角边分别为a,b,斜边为c,那么 。a2 + b2 = c2互逆1、已知: Rt⊿ ABC
中,∠C=90度,c =10,a=6,求bABCABCP例1.如图,要登上8米高的建筑物BC,为了安全需要,需使梯子底端离建筑物距离AB为6米,问至少需要多长的梯子?
8mBCA6m解:根据题意由勾股定理得:
AC2= 62 + 82`
=36+64
=100
即:AC=10(-10不合,舍去)
答:梯子至少长10米。实际应用1.如图,强大的台风使得一根旗杆在离地面9米处断裂,旗杆顶部落在离旗杆底部12米处,旗杆折断之前有多高?排除万难ABC 例2.甲乙两位探险者到沙漠进行探险,某日早晨
行走,上午10:00时,求甲乙两人的距离。1小时后,乙出发,以5千米/小时的速度向北
8:00甲先出发,以6千米/小时的速度向东行走,AOB分析:由题意可得:在⊿AOB中,∠AOB等于90度,OB表示甲走的路程,OA表示乙走的路程,AB表示10点时甲乙两人的距离。解:在Rt⊿AOB中,OA=OB=所以由勾股定理可得:答:甲乙两人的距离为13千米 学校组织野外考察活动.目的是测量一个小湖泊的最宽处有多少米?活动要求:
1.团队合作,设计出可行的测量方案。
2.找出需要测量计算所必须的数据。实地考察1.构造一个直角三角形ABC。2.测量出AC,BC的距离。3.利用勾股定理计算出AB的距离。参考方案:例3.葭生池中 今有方池一丈, 葭生其中央, 出水一尺, 引葭赴岸, 适与岸齐。 问:水深、葭长各几何? X-1X1尺解:可设葭长为x尺,则水深为(x-1)尺则有: (x-1)2+52=x2解得: x=13所以:葭长13尺,水深12尺。葭(jiá) 牛刀小试:印度有一数学家婆什迦罗曾提出过“荷花问题”:“平平湖水清可鉴, 面上半尺生红莲;
出泥不染亭亭立, 忽被强风吹一边。
渔人观看忙向前, 花离原位二尺远;
能算诸君请解题, 湖水如何知深浅?”“平平湖水清可鉴, 面上半尺生红莲; 出泥不染亭亭立, 忽被强风吹一边。
渔人观看忙向前, 花离原位二尺远;能算诸君请解题, 湖水如何知深浅?”分析:先把实际问题转化成数学问题。求:AB的长。根据勾股定理得: 解得 x = 3.75 (尺)答:湖水深3.75尺。解:设AB= x,则BD = x + 0.5,所以BC = BD = x + 0.5,在Rt△ABC中,∠BAC = 90o ,所以有:( x + 0.5 )2 = x2 + 22求:AB的长。12C例4.已知:四边形ABCD中,∠B=900,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积?3413名题鉴赏葛藤是自然界中一种聪明的植物,它自己腰杆不硬,为了享
受更多的阳光雨露,常常绕着树干盘旋而上,它还有一手绝
招,就是它绕树盘升的路线,总是沿最短路线螺旋前进!难
道植物也懂数学?通过阅读以上信息,你能设计一种方法解决下列问题吗?如果树的周长为3cm,绕一圈升高4cm,则它爬行的路线是什么?课时小结 谈谈你这节课的收获有哪些?
①会用勾股定理解决简单应用题.
②学会构造直角三角形.
③从生活中发现数学的奥妙.作业设计1、P58练习1、22、60页习题第2、6题课后探索 做一个长,宽,高分别为50厘米,40厘米,30厘米的木箱,一根长为70厘米的木棒能否放入,为什么?试用今天学过的知识说明。谢谢指导!
