华师版数学八年级上册 13.5逆命题与逆定理第3课时 角平分线课件 (共19张PPT)
文档属性
| 名称 | 华师版数学八年级上册 13.5逆命题与逆定理第3课时 角平分线课件 (共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 581.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-04 13:29:23 | ||
图片预览






文档简介
(共19张PPT)
13.5 逆命题与逆定理
第3课时 角平分线
学习目标
掌握并会证明角平分线的性质定理;
掌握并会证明角平分线的性质定理的逆定理.
温故知新
角是轴对称图形吗?
角的对称轴是什么?
角平分线的尺规作图还记得吗?
角平分线有什么性质?
是.
角平分线所在的直线.
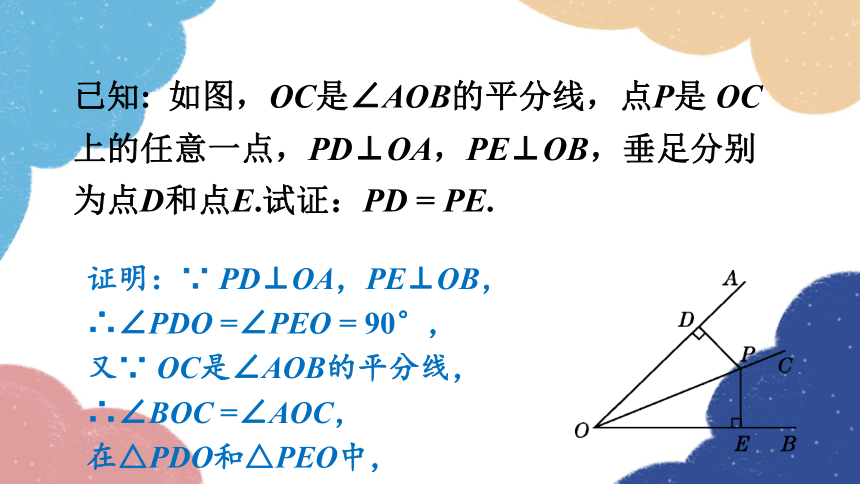
已知: 如图,OC是∠AOB的平分线,点P是 OC上的任意一点,PD⊥OA,PE⊥OB,垂足分别为点D和点E.试证:PD = PE.
分析:图中有两个直角三角形PDO和PEO,只要证明这两个三角形全等,便可证得PD = PE.
新知探索
已知: 如图,OC是∠AOB的平分线,点P是 OC上的任意一点,PD⊥OA,PE⊥OB,垂足分别为点D和点E.试证:PD = PE.
证明:∵ PD⊥OA,PE⊥OB,
∴∠PDO =∠PEO = 90°,
又∵ OC是∠AOB的平分线,
∴∠BOC =∠AOC,
在△PDO和△PEO中,
已知: 如图,OC是∠AOB的平分线,点P是 OC上的任意一点,PD⊥OA,PE⊥OB,垂足分别为点D和点E.试证:PD = PE.
∵∠PDO =∠PEO,
∠BOC =∠AOC,
OP = OP,
∴△PDO≌△PEO(A.A.S.).
∴ PD = PE(全等三角形对应边相等).
角平分线的性质定理:
角平分线上的点到角两边的距离相等.
1.点一定要在角平分线上;
2.点到角两边的距离是指点到角两边垂线段的长度;
3.角平分线的性质可用来证明两条线段相等.
注意
【例1】如图,在△ABC中,∠C = 90°,AD平分∠CAB,DE⊥AB于E,F在AC上,BE = FC.求证:BD = DF.
例题
证明:∵AD平分∠CAB,DE⊥AB于E,∠C = 90°,
∴DE = DC,∠DEB = 90°.
在△BDE和△FDC中,
∵ED=DC,∠DEB=∠C,BE=FC,
∴△BDE≌△FDC(S.A.S.),
∴BD = DF(全等三角形对应边相等).
类比上节课所学知识,你能写出角平分线的性质定理的逆命题并判断真假吗?
条件 结论
性质定理
逆命题
点在角平分线上
点到角两边的距离相等
点到角两边的距离相等
点在角平分线上
已知:如图,QD⊥OA,QE⊥OB,点D、E为垂足,QD = QE.
求证:点Q在∠AOB的平分线上.
分析:为了证明点Q在∠AOB的平分线上,可以作射线OQ,然后证明Rt △QDO≌ Rt △QEO,从而得到∠AOQ =∠BOQ.
已知:如图,QD⊥OA,QE⊥OB,点D、E为垂足,QD = QE.
求证:点Q在∠AOB的平分线上.
证明:过点O、Q作射线OQ.
∵ QD⊥OA,QE⊥OB ,
∴ ∠QDO =∠ QEO = 90°.
在 Rt△QDO和Rt△QEO中,
∵ OQ = OQ,QD = QE,
∴ Rt △QDO≌Rt △QEO (H.L.),
已知:如图,QD⊥OA,QE⊥OB,点D、E为垂足,QD = QE.
求证:点Q在∠AOB的平分线上.
∴ ∠DOQ =∠EOQ(全等三角形的
对应角相等).
∴点Q在∠AOB的平分线上.
角平分线的性质定理的逆定理:
角的内部到角两边距离相等的点在角的平分线上.
运用角平分线的性质定理的逆定理,可以证明两个角相等或一条射线是角的平分线.
注意
角平分线的性质定理的逆定理:
角的内部到角两边距离相等的点在角的平分线上.
角平分线的性质定理:
角平分线上的点到角两边的距离相等.
这两个定理互为逆定理.
思考:通过这两个定理,能证明三角形的三条角平分线交于一点吗?
试一试
证明:三角形的三条角平分线交于一点.
AO是∠BAC的平分线
BO是∠ABC的平分线
OI = OH
OG = OI
OG = OH
点O在∠BCA的平分线上
根据这个思路,你能写出证明过程吗?
练习
1.如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B .下列结论中不一定成立的是( )
A.PA = PB
B.PO平分∠APB
C.OA = OB
D.AB垂直平分OP
D
2.如图,已知在△ABC中,CD是AB边上的高,BE平分∠ABC,交CD于点E,BC = 50,
DE =14,则△BCE的面积等于________.
350
3.如图,BE = CF,DF⊥AC于点F,DE⊥AB于点E,BF和CE相交于点D.
求证:AD平分∠BAC.
证明:∵DF⊥AC于点F,DE⊥AB于点E,
∴∠DEB =∠DFC =90°.
在△BDE和△CDF中,
∵∠BDE =∠CDF,
∠DEB =∠DFC,
BE = CF,
∴△BDE≌△CDF(A.A.S.),
∴DE = DF(全等三角形对应边相等).
又∵DF⊥AC于点F,DE⊥AB于点E,
∴AD平分∠BAC.
本节课都学了什么知识?
角平分线的性质定理;
角平分线的性质定理的逆定理;
三角形的三条角平分线交于一点.
课堂小结
13.5 逆命题与逆定理
第3课时 角平分线
学习目标
掌握并会证明角平分线的性质定理;
掌握并会证明角平分线的性质定理的逆定理.
温故知新
角是轴对称图形吗?
角的对称轴是什么?
角平分线的尺规作图还记得吗?
角平分线有什么性质?
是.
角平分线所在的直线.
已知: 如图,OC是∠AOB的平分线,点P是 OC上的任意一点,PD⊥OA,PE⊥OB,垂足分别为点D和点E.试证:PD = PE.
分析:图中有两个直角三角形PDO和PEO,只要证明这两个三角形全等,便可证得PD = PE.
新知探索
已知: 如图,OC是∠AOB的平分线,点P是 OC上的任意一点,PD⊥OA,PE⊥OB,垂足分别为点D和点E.试证:PD = PE.
证明:∵ PD⊥OA,PE⊥OB,
∴∠PDO =∠PEO = 90°,
又∵ OC是∠AOB的平分线,
∴∠BOC =∠AOC,
在△PDO和△PEO中,
已知: 如图,OC是∠AOB的平分线,点P是 OC上的任意一点,PD⊥OA,PE⊥OB,垂足分别为点D和点E.试证:PD = PE.
∵∠PDO =∠PEO,
∠BOC =∠AOC,
OP = OP,
∴△PDO≌△PEO(A.A.S.).
∴ PD = PE(全等三角形对应边相等).
角平分线的性质定理:
角平分线上的点到角两边的距离相等.
1.点一定要在角平分线上;
2.点到角两边的距离是指点到角两边垂线段的长度;
3.角平分线的性质可用来证明两条线段相等.
注意
【例1】如图,在△ABC中,∠C = 90°,AD平分∠CAB,DE⊥AB于E,F在AC上,BE = FC.求证:BD = DF.
例题
证明:∵AD平分∠CAB,DE⊥AB于E,∠C = 90°,
∴DE = DC,∠DEB = 90°.
在△BDE和△FDC中,
∵ED=DC,∠DEB=∠C,BE=FC,
∴△BDE≌△FDC(S.A.S.),
∴BD = DF(全等三角形对应边相等).
类比上节课所学知识,你能写出角平分线的性质定理的逆命题并判断真假吗?
条件 结论
性质定理
逆命题
点在角平分线上
点到角两边的距离相等
点到角两边的距离相等
点在角平分线上
已知:如图,QD⊥OA,QE⊥OB,点D、E为垂足,QD = QE.
求证:点Q在∠AOB的平分线上.
分析:为了证明点Q在∠AOB的平分线上,可以作射线OQ,然后证明Rt △QDO≌ Rt △QEO,从而得到∠AOQ =∠BOQ.
已知:如图,QD⊥OA,QE⊥OB,点D、E为垂足,QD = QE.
求证:点Q在∠AOB的平分线上.
证明:过点O、Q作射线OQ.
∵ QD⊥OA,QE⊥OB ,
∴ ∠QDO =∠ QEO = 90°.
在 Rt△QDO和Rt△QEO中,
∵ OQ = OQ,QD = QE,
∴ Rt △QDO≌Rt △QEO (H.L.),
已知:如图,QD⊥OA,QE⊥OB,点D、E为垂足,QD = QE.
求证:点Q在∠AOB的平分线上.
∴ ∠DOQ =∠EOQ(全等三角形的
对应角相等).
∴点Q在∠AOB的平分线上.
角平分线的性质定理的逆定理:
角的内部到角两边距离相等的点在角的平分线上.
运用角平分线的性质定理的逆定理,可以证明两个角相等或一条射线是角的平分线.
注意
角平分线的性质定理的逆定理:
角的内部到角两边距离相等的点在角的平分线上.
角平分线的性质定理:
角平分线上的点到角两边的距离相等.
这两个定理互为逆定理.
思考:通过这两个定理,能证明三角形的三条角平分线交于一点吗?
试一试
证明:三角形的三条角平分线交于一点.
AO是∠BAC的平分线
BO是∠ABC的平分线
OI = OH
OG = OI
OG = OH
点O在∠BCA的平分线上
根据这个思路,你能写出证明过程吗?
练习
1.如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B .下列结论中不一定成立的是( )
A.PA = PB
B.PO平分∠APB
C.OA = OB
D.AB垂直平分OP
D
2.如图,已知在△ABC中,CD是AB边上的高,BE平分∠ABC,交CD于点E,BC = 50,
DE =14,则△BCE的面积等于________.
350
3.如图,BE = CF,DF⊥AC于点F,DE⊥AB于点E,BF和CE相交于点D.
求证:AD平分∠BAC.
证明:∵DF⊥AC于点F,DE⊥AB于点E,
∴∠DEB =∠DFC =90°.
在△BDE和△CDF中,
∵∠BDE =∠CDF,
∠DEB =∠DFC,
BE = CF,
∴△BDE≌△CDF(A.A.S.),
∴DE = DF(全等三角形对应边相等).
又∵DF⊥AC于点F,DE⊥AB于点E,
∴AD平分∠BAC.
本节课都学了什么知识?
角平分线的性质定理;
角平分线的性质定理的逆定理;
三角形的三条角平分线交于一点.
课堂小结
