北师大版八年级数学上册 第1章勾股定理 单元同步练习题 (含答案)
文档属性
| 名称 | 北师大版八年级数学上册 第1章勾股定理 单元同步练习题 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 552.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-04 13:45:07 | ||
图片预览


文档简介
2023-2024学年北师大版八年级数学上册《第1章勾股定理》单元同步练习题(附答案)
一、单选题
1.下列各组数中,是勾股数的为( )
A.,, B.,, C.,, D.,,
2.在中,斜边,则的值为( )
A. B. C. D.无法计算
3.已知中,,,,斜边边上的高的长度为( )
A. B.5 C. D.10
4.如图,一棵大树被台风刮断,若树在离地面处折断,树顶端落在离树底部处,则树折断之前高( )
A. B. C. D.
5.如图所示,有一块直角三角形纸片,,,将斜边翻折,使点B落在直角边的延长线上的点E处,折痕为,则的长为( ).
A.1cm B.1.5cm C.2cm D.3cm
6.如图一个三级台阶,它的每一级的长宽高分别是5,3和1,和是这个台阶的两个相对的端点,点上有一只蚂蚁,想到点去吃可口的食物,则蚂蚁沿着台阶面爬到点的最短路程长为( )
A.10 B.11 C.12 D.13
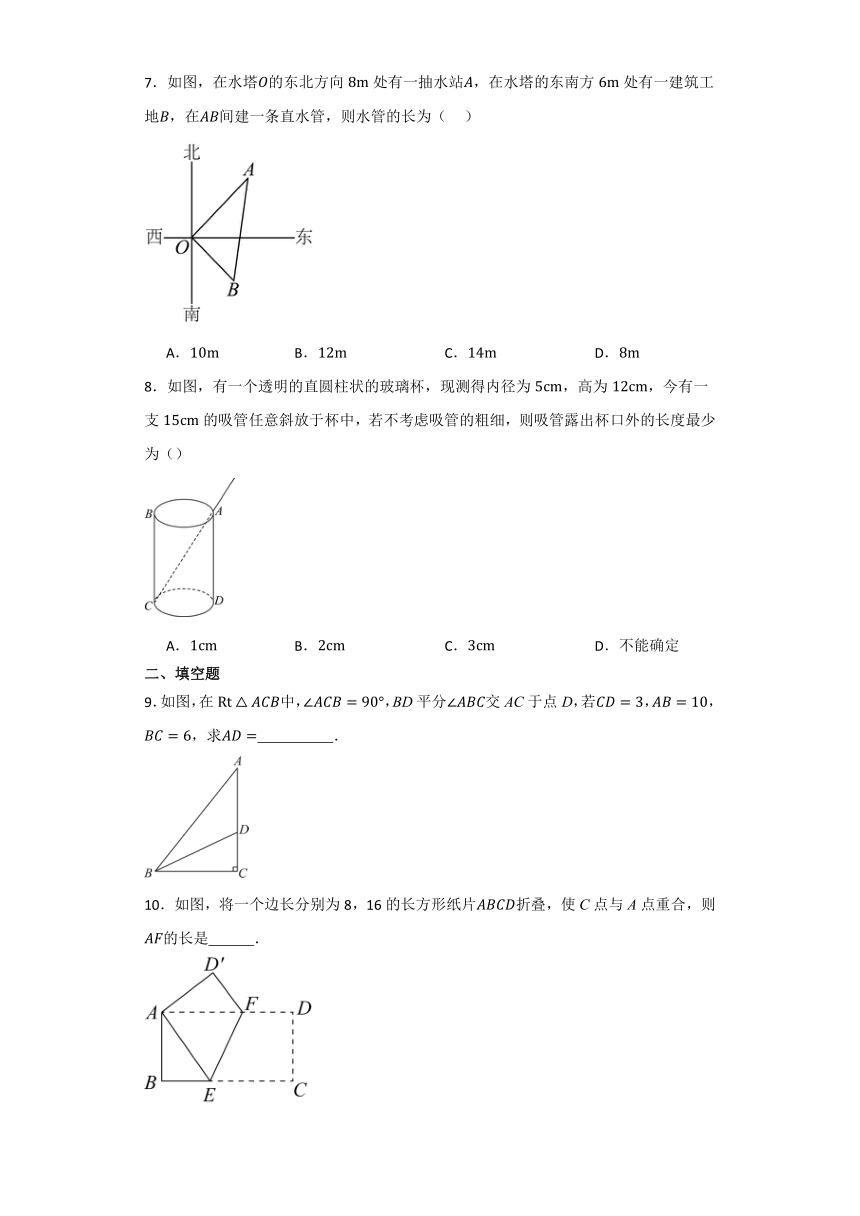
7.如图,在水塔的东北方向处有一抽水站,在水塔的东南方处有一建筑工地,在间建一条直水管,则水管的长为( )
A. B. C. D.
8.如图,有一个透明的直圆柱状的玻璃杯,现测得内径为,高为,今有一支的吸管任意斜放于杯中,若不考虑吸管的粗细,则吸管露出杯口外的长度最少为()
A. B. C. D.不能确定
二、填空题
9.如图,在中,,BD平分交AC于点D,若,,,求 .
10.如图,将一个边长分别为8,16的长方形纸片折叠,使C点与A点重合,则的长是 .
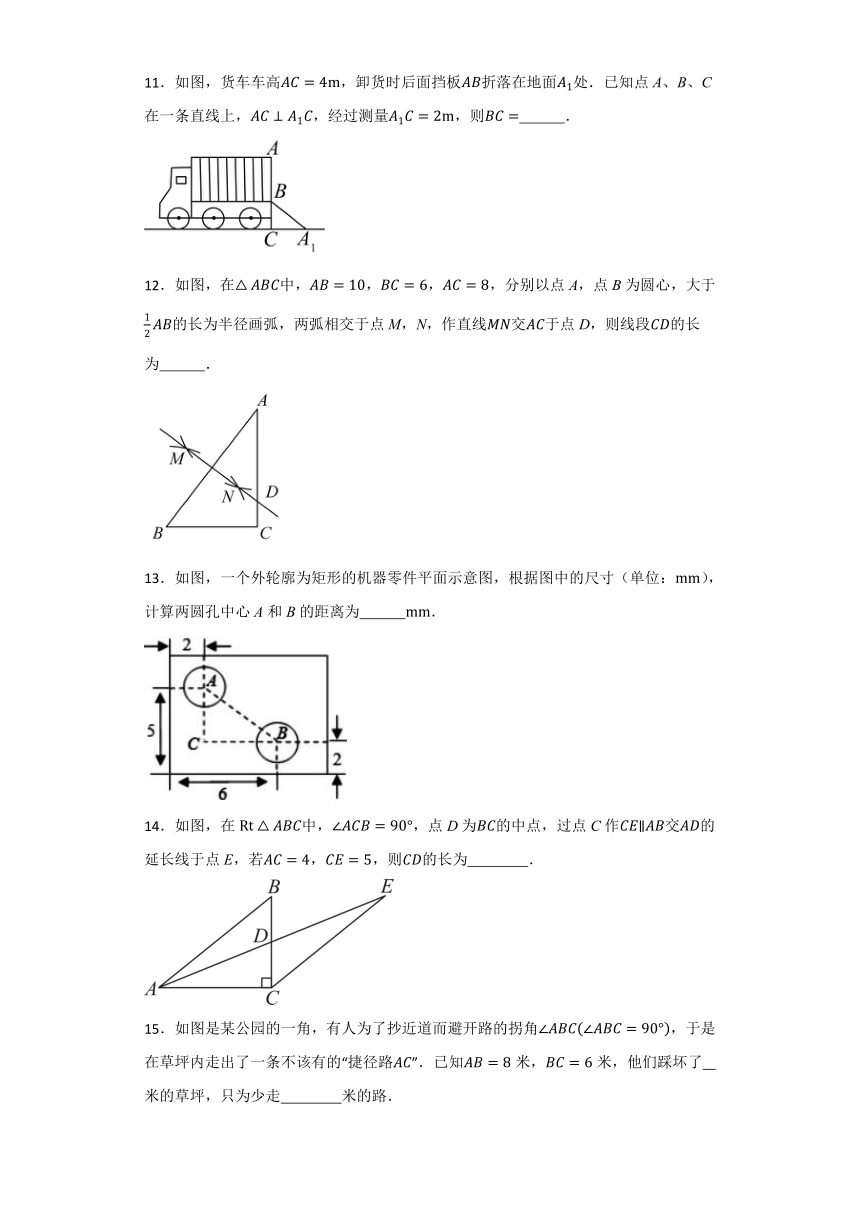
11.如图,货车车高,卸货时后面挡板折落在地面处.已知点A、B、C在一条直线上,,经过测量,则 .
12.如图,在中,,,,分别以点A,点B为圆心,大于的长为半径画弧,两弧相交于点M,N,作直线交于点D,则线段的长为 .
13.如图,一个外轮廓为矩形的机器零件平面示意图,根据图中的尺寸(单位:),计算两圆孔中心A和B的距离为 .
14.如图,在中,,点D为的中点,过点C作交的延长线于点E,若,,则的长为 .
15.如图是某公园的一角,有人为了抄近道而避开路的拐角,于是在草坪内走出了一条不该有的“捷径路”.已知米,米,他们踩坏了 米的草坪,只为少走 米的路.
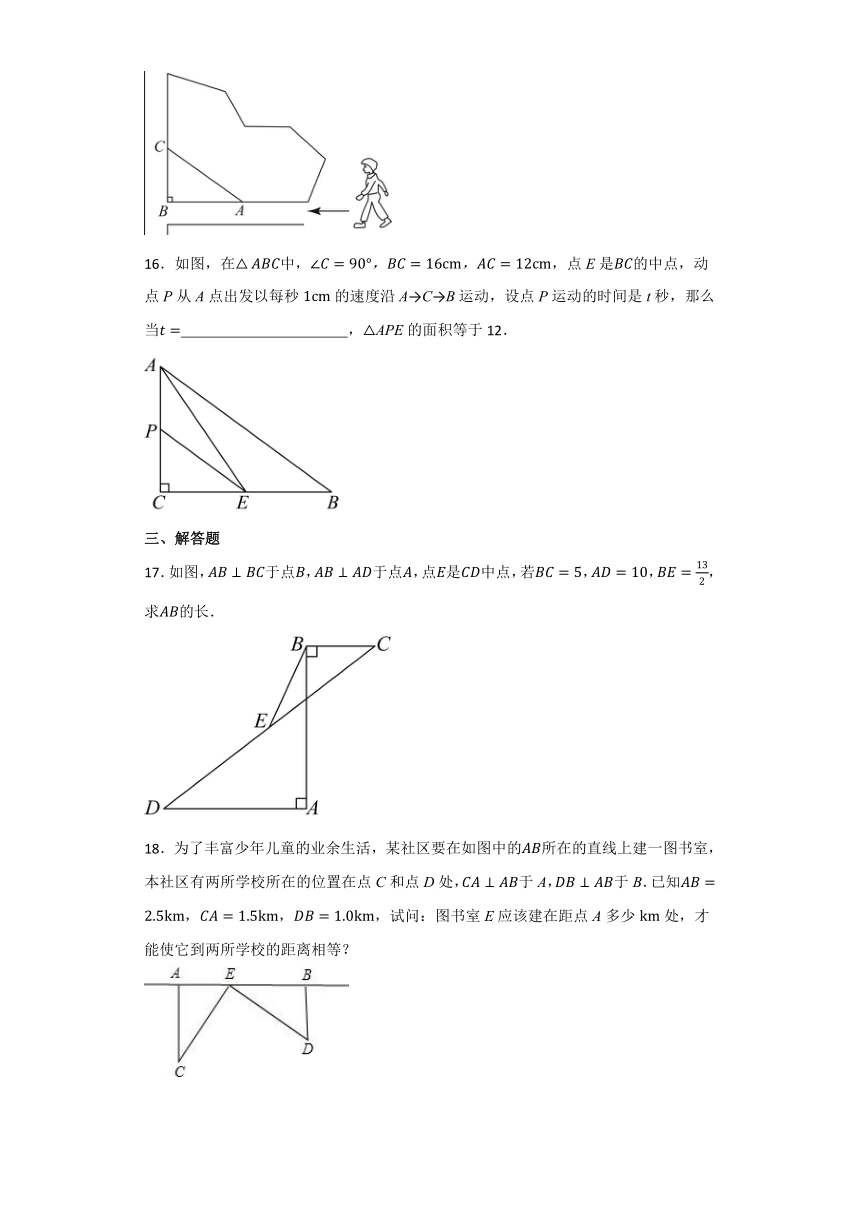
16.如图,在中,,点E是的中点,动点P从A点出发以每秒的速度沿A→C→B运动,设点P运动的时间是t秒,那么当 ,△APE的面积等于12.
三、解答题
17.如图,于点,于点,点是中点,若,,,求的长.
18.为了丰富少年儿童的业余生活,某社区要在如图中的所在的直线上建一图书室,本社区有两所学校所在的位置在点C和点D处,于A,于B.已知,,,试问:图书室E应该建在距点A多少处,才能使它到两所学校的距离相等?
19.一架方梯长25米,如图所示,斜靠在一面上:
(1)若梯子底端离墙7米,这个梯子的顶端距地面有多高?
(2)在(1)的条件下,如果梯子的顶端下滑了4米,那么梯子的底端在水平方向滑动了几米?
20.我们发现,用不同的方式表示同一图形的面积可以解决线段长度之间关系的有关问题,这种方法称为等面积法,这是一种重要的数学方法,请你用等面积法来探究下列两个问题:
(1)如图1是著名的“赵爽弦图”,由四个全等的直角三角形拼成,请你用它验证勾股定理;
(2)如图2,在中,是边上高,,,求的长度.
21.问题探究
(1)如图1,M,N分别是正方形的边,上的动点,,,,求的长.
深入探究
(2)若把(1)中的条件改为,,求的长.
类比探究
(3)在(2)的条件下,如图2,当点M,N分别在正方形的边,的延长线上时,请直接写出的长度.
22.如图1,长方形(对边平行且相等,四个角都是直角)中,,,点在边上,且不与点、重合,直线与的延长线交于点.
(1)当点是的中点时,求证:;
(2)将沿直线折叠得到,点落在长方形的内部,延长交直线于点.
①证明,并求出在()条件下的值;
②连接,求周长的最小值.
参考答案
1.解:、,这组数不是勾股数;
B、,这组数不是勾股数;
C、,这组数是勾股数;
D、,这组数不是勾股数,
故选:C.
2.解:∵在中,斜边为,
∴,
∵,
∴,
∴,
故选.
3.解:∵,,,
∴根据勾股定理可得:,
∵,
∴,即,
解得:,
故选:A.
4.解:如图,设,,
∴,
∴树高为,
故选B.
5.解:在中,,
根据折叠的性质可知:.
∵,
∴.
故选A.
6.解:如图所示,
∵三级台阶平面展开图为长方形,宽为5,长为,
∴蚂蚁沿台阶面爬行到点最短路程是此长方形的对角线长,
由勾股定理得,
则蚂蚁沿着台阶面爬到点最短路程是13.
故选:D.
7.解:根据题意可知,,,
所以,.
所以,水管的长为.
故选:A.
8.解∶,
,
露出杯口外的长度为.
故答案为:B.
9.解:在中,,,
∴,
∵,
∴,
故答案为:5.
10.解:根据折叠的性质知,,,
∵长方形,
,,
,
,
∴,
由勾股定理得,,
即,
解得,
.
故答案为:10.
11.解:由题意得,,,
设 ,则,
在中,,
即:,
解得:.
∴,
故答案为:.
12.解:连接.
由作图可知,点D在线段的垂直平分线上,则.
设,则.
∵,
∴
∴.
在中,,
即
解得:
故答案为:
13.解:由图可知:,,
根据勾股定理可得:,
故答案为:5.
14.解: ,
,
点D为的中点,
,
又 ,
,
,
中,,,
,
.
故答案为:.
15. 解:在中,米,米,
∴,
∴踩坏了10米的草坪,
∵.
∴只为少走4米的路.
故答案为:10,4
16.解:∵,,,
∴,
∵点E是的中点,
∴,
.
当点P在线段上运动时,
∵的面积等于12,即,
∴,
∴秒;
当点P在线段运动时上且在点E的右边时,,如图2所示,
同理可知,
∴秒;
当点P在线段上运动且在点E的左边时,如图3所示,
同理可知,
∴秒;
故答案为∶3或18或22.
17.解:延长交于点,
,,
,
,
,
点是中点,
,
在和中,
,
,
,,
,
,
在中,,
,
的长为12.
18.解:设图书室E应建在距A点x千米处,才能使它到两所学校的距离相等,
则千米;
∵,,
∴,,
∵,
∴,
即,
解得:,
答:图书室E应建在距A点千米处,才能使它到两所学校的距离相等.
19.(1)解:在中,(米),(米),
∴(米),
答:梯子的顶端距地面24米;
(2)解:在中,(米),
∴(米),
∴(米),
答:梯子的底端在水平方向滑动了8米.
20.(1)解:大正方形面积为,直角三角形面积为,小正方形面积为:,
即.
(2)在中,
,
由勾股定理,得:
,
,
.
21.解:(1)如图,延长至点B1,使.
∵四边形是正方形,
∴.
在和中,
∴.
∴.
又∵,
∴,
∴.
在和中,
∴.
∴.
(2)如图,过点A作于点P,则.
∵四边形是正方形,
∴,
∴.
又∵,
∴.
在和中,,
∴.
∴.
在和中,,
∴.
∴.
∵,
∴.
设,则,
在中,由勾股定理得,
∴,解得,
∴.
(3)如图,延长,过A作的延长线于点E.
由正方形知,则B,
∵
∴.即
∵
∴
∴,又
∴.
在与中,
∴
∴
由,知
在中,设
则.
由勾股定理得,,
即:
解得.
∴的长度为.
22.(1)证明:在长方形中,
,,
点P是的中点,
,
;
(2)解:①在长方形中,,
,
由折叠得,
,
,
在长方形中,,,
,
点P是的中点,
,
由折叠得,,,
设,则,
,
在中,,
,
解得,即;
②由折叠得,,
的周长,
连接,,
,
当点恰好位于对角线上时,最小,
在中,,,
,
′的最小值,
∴周长的最小值.
一、单选题
1.下列各组数中,是勾股数的为( )
A.,, B.,, C.,, D.,,
2.在中,斜边,则的值为( )
A. B. C. D.无法计算
3.已知中,,,,斜边边上的高的长度为( )
A. B.5 C. D.10
4.如图,一棵大树被台风刮断,若树在离地面处折断,树顶端落在离树底部处,则树折断之前高( )
A. B. C. D.
5.如图所示,有一块直角三角形纸片,,,将斜边翻折,使点B落在直角边的延长线上的点E处,折痕为,则的长为( ).
A.1cm B.1.5cm C.2cm D.3cm
6.如图一个三级台阶,它的每一级的长宽高分别是5,3和1,和是这个台阶的两个相对的端点,点上有一只蚂蚁,想到点去吃可口的食物,则蚂蚁沿着台阶面爬到点的最短路程长为( )
A.10 B.11 C.12 D.13
7.如图,在水塔的东北方向处有一抽水站,在水塔的东南方处有一建筑工地,在间建一条直水管,则水管的长为( )
A. B. C. D.
8.如图,有一个透明的直圆柱状的玻璃杯,现测得内径为,高为,今有一支的吸管任意斜放于杯中,若不考虑吸管的粗细,则吸管露出杯口外的长度最少为()
A. B. C. D.不能确定
二、填空题
9.如图,在中,,BD平分交AC于点D,若,,,求 .
10.如图,将一个边长分别为8,16的长方形纸片折叠,使C点与A点重合,则的长是 .
11.如图,货车车高,卸货时后面挡板折落在地面处.已知点A、B、C在一条直线上,,经过测量,则 .
12.如图,在中,,,,分别以点A,点B为圆心,大于的长为半径画弧,两弧相交于点M,N,作直线交于点D,则线段的长为 .
13.如图,一个外轮廓为矩形的机器零件平面示意图,根据图中的尺寸(单位:),计算两圆孔中心A和B的距离为 .
14.如图,在中,,点D为的中点,过点C作交的延长线于点E,若,,则的长为 .
15.如图是某公园的一角,有人为了抄近道而避开路的拐角,于是在草坪内走出了一条不该有的“捷径路”.已知米,米,他们踩坏了 米的草坪,只为少走 米的路.
16.如图,在中,,点E是的中点,动点P从A点出发以每秒的速度沿A→C→B运动,设点P运动的时间是t秒,那么当 ,△APE的面积等于12.
三、解答题
17.如图,于点,于点,点是中点,若,,,求的长.
18.为了丰富少年儿童的业余生活,某社区要在如图中的所在的直线上建一图书室,本社区有两所学校所在的位置在点C和点D处,于A,于B.已知,,,试问:图书室E应该建在距点A多少处,才能使它到两所学校的距离相等?
19.一架方梯长25米,如图所示,斜靠在一面上:
(1)若梯子底端离墙7米,这个梯子的顶端距地面有多高?
(2)在(1)的条件下,如果梯子的顶端下滑了4米,那么梯子的底端在水平方向滑动了几米?
20.我们发现,用不同的方式表示同一图形的面积可以解决线段长度之间关系的有关问题,这种方法称为等面积法,这是一种重要的数学方法,请你用等面积法来探究下列两个问题:
(1)如图1是著名的“赵爽弦图”,由四个全等的直角三角形拼成,请你用它验证勾股定理;
(2)如图2,在中,是边上高,,,求的长度.
21.问题探究
(1)如图1,M,N分别是正方形的边,上的动点,,,,求的长.
深入探究
(2)若把(1)中的条件改为,,求的长.
类比探究
(3)在(2)的条件下,如图2,当点M,N分别在正方形的边,的延长线上时,请直接写出的长度.
22.如图1,长方形(对边平行且相等,四个角都是直角)中,,,点在边上,且不与点、重合,直线与的延长线交于点.
(1)当点是的中点时,求证:;
(2)将沿直线折叠得到,点落在长方形的内部,延长交直线于点.
①证明,并求出在()条件下的值;
②连接,求周长的最小值.
参考答案
1.解:、,这组数不是勾股数;
B、,这组数不是勾股数;
C、,这组数是勾股数;
D、,这组数不是勾股数,
故选:C.
2.解:∵在中,斜边为,
∴,
∵,
∴,
∴,
故选.
3.解:∵,,,
∴根据勾股定理可得:,
∵,
∴,即,
解得:,
故选:A.
4.解:如图,设,,
∴,
∴树高为,
故选B.
5.解:在中,,
根据折叠的性质可知:.
∵,
∴.
故选A.
6.解:如图所示,
∵三级台阶平面展开图为长方形,宽为5,长为,
∴蚂蚁沿台阶面爬行到点最短路程是此长方形的对角线长,
由勾股定理得,
则蚂蚁沿着台阶面爬到点最短路程是13.
故选:D.
7.解:根据题意可知,,,
所以,.
所以,水管的长为.
故选:A.
8.解∶,
,
露出杯口外的长度为.
故答案为:B.
9.解:在中,,,
∴,
∵,
∴,
故答案为:5.
10.解:根据折叠的性质知,,,
∵长方形,
,,
,
,
∴,
由勾股定理得,,
即,
解得,
.
故答案为:10.
11.解:由题意得,,,
设 ,则,
在中,,
即:,
解得:.
∴,
故答案为:.
12.解:连接.
由作图可知,点D在线段的垂直平分线上,则.
设,则.
∵,
∴
∴.
在中,,
即
解得:
故答案为:
13.解:由图可知:,,
根据勾股定理可得:,
故答案为:5.
14.解: ,
,
点D为的中点,
,
又 ,
,
,
中,,,
,
.
故答案为:.
15. 解:在中,米,米,
∴,
∴踩坏了10米的草坪,
∵.
∴只为少走4米的路.
故答案为:10,4
16.解:∵,,,
∴,
∵点E是的中点,
∴,
.
当点P在线段上运动时,
∵的面积等于12,即,
∴,
∴秒;
当点P在线段运动时上且在点E的右边时,,如图2所示,
同理可知,
∴秒;
当点P在线段上运动且在点E的左边时,如图3所示,
同理可知,
∴秒;
故答案为∶3或18或22.
17.解:延长交于点,
,,
,
,
,
点是中点,
,
在和中,
,
,
,,
,
,
在中,,
,
的长为12.
18.解:设图书室E应建在距A点x千米处,才能使它到两所学校的距离相等,
则千米;
∵,,
∴,,
∵,
∴,
即,
解得:,
答:图书室E应建在距A点千米处,才能使它到两所学校的距离相等.
19.(1)解:在中,(米),(米),
∴(米),
答:梯子的顶端距地面24米;
(2)解:在中,(米),
∴(米),
∴(米),
答:梯子的底端在水平方向滑动了8米.
20.(1)解:大正方形面积为,直角三角形面积为,小正方形面积为:,
即.
(2)在中,
,
由勾股定理,得:
,
,
.
21.解:(1)如图,延长至点B1,使.
∵四边形是正方形,
∴.
在和中,
∴.
∴.
又∵,
∴,
∴.
在和中,
∴.
∴.
(2)如图,过点A作于点P,则.
∵四边形是正方形,
∴,
∴.
又∵,
∴.
在和中,,
∴.
∴.
在和中,,
∴.
∴.
∵,
∴.
设,则,
在中,由勾股定理得,
∴,解得,
∴.
(3)如图,延长,过A作的延长线于点E.
由正方形知,则B,
∵
∴.即
∵
∴
∴,又
∴.
在与中,
∴
∴
由,知
在中,设
则.
由勾股定理得,,
即:
解得.
∴的长度为.
22.(1)证明:在长方形中,
,,
点P是的中点,
,
;
(2)解:①在长方形中,,
,
由折叠得,
,
,
在长方形中,,,
,
点P是的中点,
,
由折叠得,,,
设,则,
,
在中,,
,
解得,即;
②由折叠得,,
的周长,
连接,,
,
当点恰好位于对角线上时,最小,
在中,,,
,
′的最小值,
∴周长的最小值.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
