指数函数(湖南省湘潭市湘潭县)
图片预览



文档简介
课件19张PPT。2.6 指数函数 (2)1. 定义: 函数
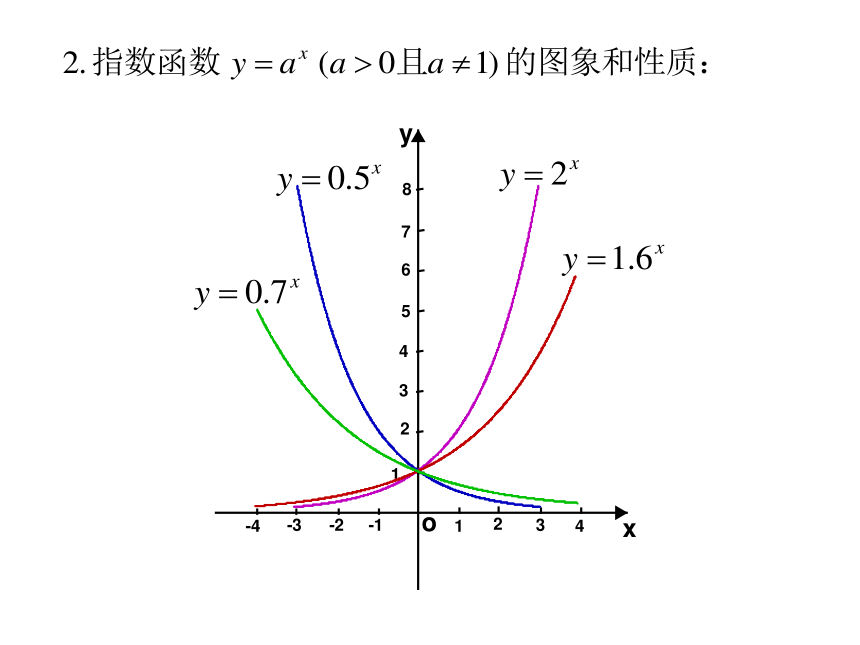
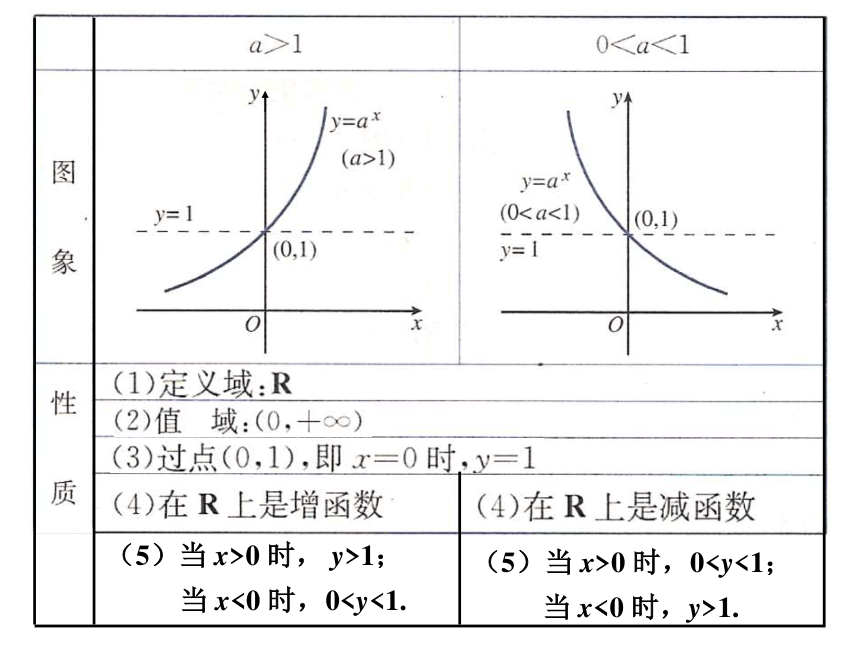
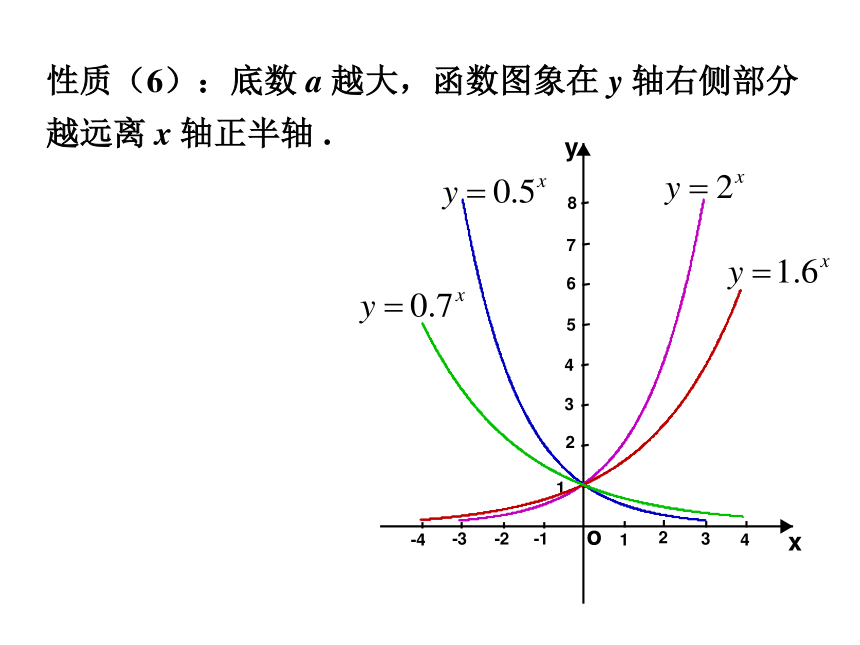
叫指数函数,其中x是自变量,函数的定义域是R.复 习:(5)当 x>0 时, y>1; 当 x<0 时,00 时,01.性质(6):底数 a 越大,函数图象在 y 轴右侧部分
越远离 x 轴正半轴 .例1 一种放射性物质不断变化为其他物质,每经过一
年剩留的质量约是原来的84%.画出这种物质的剩留量
随时间变化的图象,并从图象上求出约经过多少年,
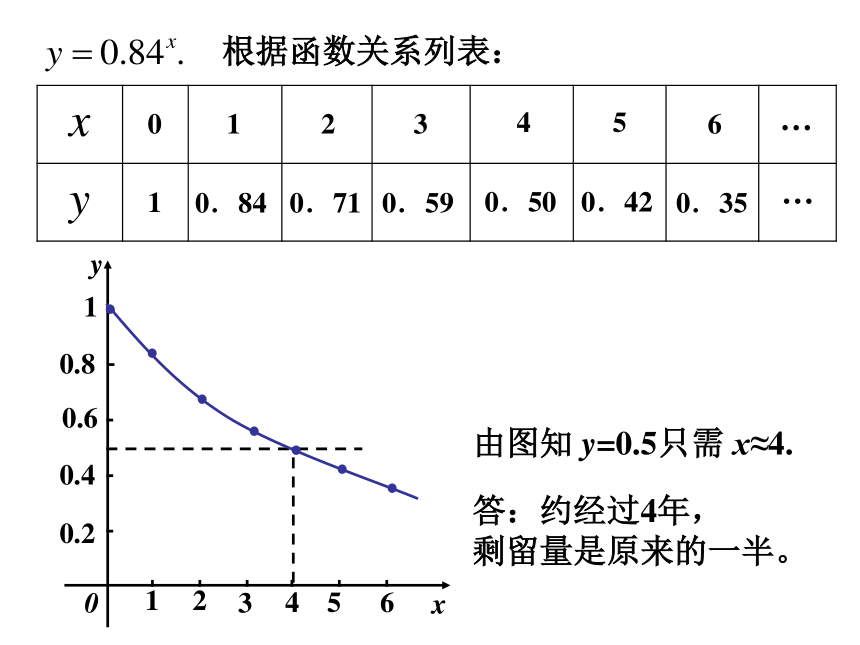
剩留量是原来的一半(结果保留一个有效数字)。解:设最初的质量是1,经过 x 年,剩留量是 y .则经过1年,剩留量经过2年,剩留量……经过x年,剩留量经过3年,剩留量根据函数关系列表:10.840.710.590.500.420.35…0123456…由图知 y=0.5只需 x≈4. 答:约经过4年,
剩留量是原来的一半。例2 说明下列函数的图象与指数函数 y = 2x
的图象的关系,并画出它们的示意图:
(1) y = 2x+1 ; (2) y = 2x-2 .解:(1)比较函数 y = 2x+1 与 y = 2x 的关系 : y = 2-3+1 与 y = 2-2 y = 2-2+1 与 y = 2-1 y = 22+1 与 y = 23……由此可知,将指数函数 y = 2x
的图象向左平移1个单位长度,
就得到函数 y = 2x+1 的图象. y = 2x y = 2x+1相等,相等,相等,例2 说明下列函数的图象与指数函数 y = 2x
的图象的关系,并画出它们的示意图:
(1) y = 2x+1 ; (2) y = 2x-2 .解:(2)比较函数 y = 2x-2 与 y = 2x 的关系 : y = 2-1-2 与 y = 2-3 y = 20-2 与 y = 2-2 y = 23-2 与 y = 21……由此可知,将指数函数 y = 2x
的图象向右平移2个单位长度,
就得到函数 y = 2x-2 的图象. y = 2x y = 2x-2相等,相等,相等,将 y=f(x) 的图象向左平移a个单位(a>0) 将 y=f(x) 的图象向右平移a个单位(a>0) 将 y=f(x) 的图象向上平移a个单位(a>0) 将 y=f(x) 的图象向下平移a个单位(a>0) 可得到 y=f(x+a) 的图象;结论:一般地,可得到 y=f(x-a) 的图象;可得到 y= f(x)+a 的图象;可得到 y= f(x)-a 的图象 .例3.比较大小解:解:解:由指数函数的性质知解:另解:利用指数函数性质比较幂的大小要注意三点:说明:或利用性质:底数 a 越大,函数图象在 y 轴右侧部分越远离 x 轴正半轴 .课堂练习:求函数 解:要使函数有意义,只需满足:变式引申:解:要使函数有意义,只需满足:作业: 习题2.6 1,2,3,4,5.P 73 练习:1,2.
叫指数函数,其中x是自变量,函数的定义域是R.复 习:(5)当 x>0 时, y>1; 当 x<0 时,0
越远离 x 轴正半轴 .例1 一种放射性物质不断变化为其他物质,每经过一
年剩留的质量约是原来的84%.画出这种物质的剩留量
随时间变化的图象,并从图象上求出约经过多少年,
剩留量是原来的一半(结果保留一个有效数字)。解:设最初的质量是1,经过 x 年,剩留量是 y .则经过1年,剩留量经过2年,剩留量……经过x年,剩留量经过3年,剩留量根据函数关系列表:10.840.710.590.500.420.35…0123456…由图知 y=0.5只需 x≈4. 答:约经过4年,
剩留量是原来的一半。例2 说明下列函数的图象与指数函数 y = 2x
的图象的关系,并画出它们的示意图:
(1) y = 2x+1 ; (2) y = 2x-2 .解:(1)比较函数 y = 2x+1 与 y = 2x 的关系 : y = 2-3+1 与 y = 2-2 y = 2-2+1 与 y = 2-1 y = 22+1 与 y = 23……由此可知,将指数函数 y = 2x
的图象向左平移1个单位长度,
就得到函数 y = 2x+1 的图象. y = 2x y = 2x+1相等,相等,相等,例2 说明下列函数的图象与指数函数 y = 2x
的图象的关系,并画出它们的示意图:
(1) y = 2x+1 ; (2) y = 2x-2 .解:(2)比较函数 y = 2x-2 与 y = 2x 的关系 : y = 2-1-2 与 y = 2-3 y = 20-2 与 y = 2-2 y = 23-2 与 y = 21……由此可知,将指数函数 y = 2x
的图象向右平移2个单位长度,
就得到函数 y = 2x-2 的图象. y = 2x y = 2x-2相等,相等,相等,将 y=f(x) 的图象向左平移a个单位(a>0) 将 y=f(x) 的图象向右平移a个单位(a>0) 将 y=f(x) 的图象向上平移a个单位(a>0) 将 y=f(x) 的图象向下平移a个单位(a>0) 可得到 y=f(x+a) 的图象;结论:一般地,可得到 y=f(x-a) 的图象;可得到 y= f(x)+a 的图象;可得到 y= f(x)-a 的图象 .例3.比较大小解:解:解:由指数函数的性质知解:另解:利用指数函数性质比较幂的大小要注意三点:说明:或利用性质:底数 a 越大,函数图象在 y 轴右侧部分越远离 x 轴正半轴 .课堂练习:求函数 解:要使函数有意义,只需满足:变式引申:解:要使函数有意义,只需满足:作业: 习题2.6 1,2,3,4,5.P 73 练习:1,2.
