《抛物线及其标准方程》课件1
图片预览




文档简介
课件16张PPT。2018年12月20日星期四 (选修2-1)第二章 圆锥曲线与方程2.4抛物线
2.4.1抛物线及其标准方程xy复习回顾 二次函数
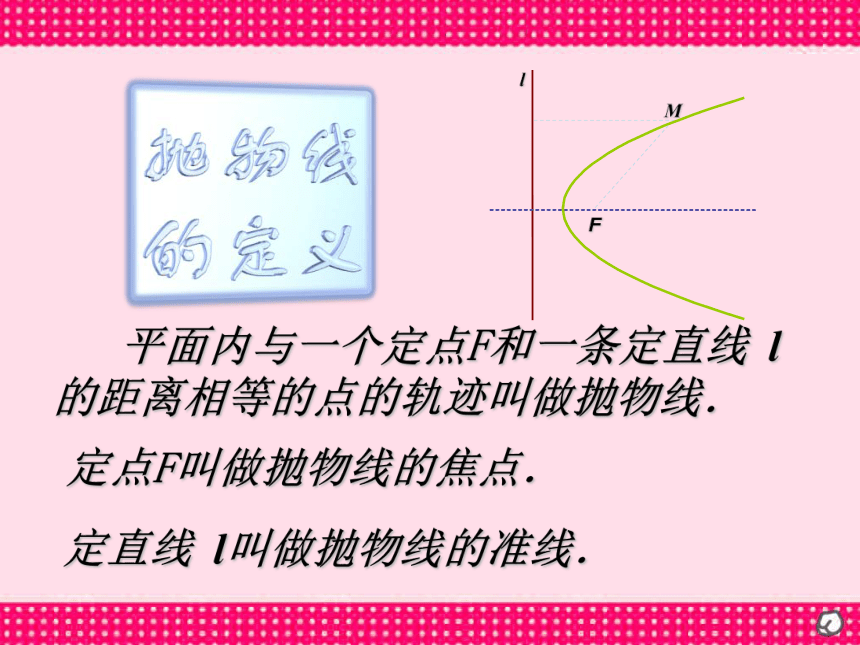
的图象是怎样的? 是一条抛物线,对称轴为顶点坐标为 平面内与一个定点F和一条定直线 l
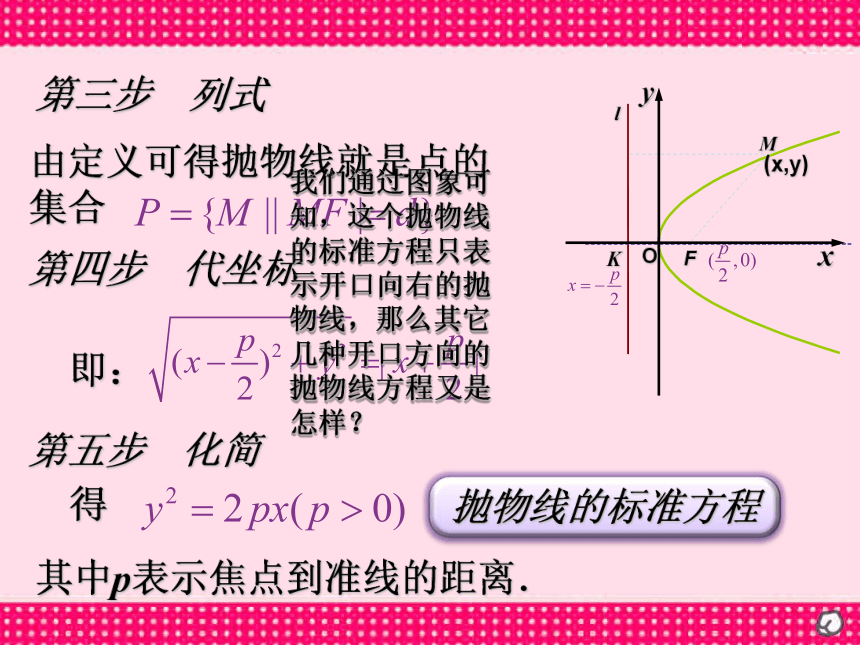
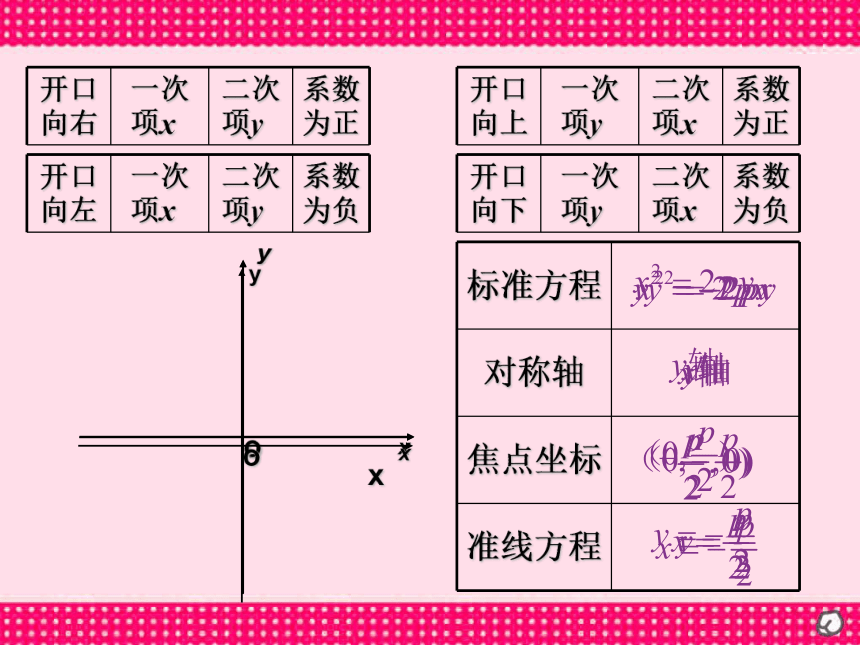
的距离相等的点的轨迹叫做抛物线.定点F叫做抛物线的焦点.定直线 l叫做抛物线的准线. 第二步 设点第一步 建立直角坐标系yxO(x,y)设F在直线l上的垂足为K,以FK的中点为坐标原点,以KF为x轴,建立直角坐标系.K那么焦点F的坐标为设|KF|=p(p>0),准线l上的方程为设M(x, y)点M到l的距离为d由定义可得抛物线就是点的集合第三步 列式第四步 代坐标第五步 化简得抛物线的标准方程即:yxO(x,y)K其中p表示焦点到准线的距离.我们通过图象可知,这个抛物线的标准方程只表示开口向右的抛物线,那么其它几种开口方向的抛物线方程又是怎样?xyoxyoxyo口诀:
一次项定轴,系数定方向;焦点与方程同号,准线与方程异号. (1)已知抛物线的标准方程是 ,求它的焦点坐标和准线方程;
(2)已知抛物线的焦点是F(0,-2),求它的标准方程. 求下列抛物线的焦点坐标和准线方程:(1)2p=20,故p=10,
焦点在x轴正方向,
焦点(5,0),准线为x=-5(2)2p= ,故p= ,
焦点在y轴正方向,
焦点 ,准线为焦点在x轴负方向,
焦点 ,准线为(3)先化为标准方程
2p= ,故p= ,
(4)先化为标准方程
求下列抛物线的焦点坐标和准线方程:2p=8,故p=4,
焦点在x轴负方向,
焦点(0,-2),准线为y=2 根据下列条件写出抛物线的
标准方程:(1)焦点是F(3,0);(2)准线方程是x=-1/4;(3)焦点到准线的距离是2. 一种卫星接收天线的轴截面如图所示.卫星波束呈近似平行状态射入轴截面为抛物线的接收天线,经反射聚集到焦点处.已知接收天线的口径为4.8m,深度为0.5m,求抛物线的标准方程和焦点坐标.oyxABF解:如图,建立直角坐标系,设抛物线的标准方程是
y2=2px(p>0).易知A (0.5,2.4),代入方程得p=5.76.2.42=2p×0.5所以,所求抛物线为y2=11.52x,
焦点坐标为(2.88,0).抛物线的定义抛物线的标准方程课后再做好复习巩固.
谢谢!再见!
2.4.1抛物线及其标准方程xy复习回顾 二次函数
的图象是怎样的? 是一条抛物线,对称轴为顶点坐标为 平面内与一个定点F和一条定直线 l
的距离相等的点的轨迹叫做抛物线.定点F叫做抛物线的焦点.定直线 l叫做抛物线的准线. 第二步 设点第一步 建立直角坐标系yxO(x,y)设F在直线l上的垂足为K,以FK的中点为坐标原点,以KF为x轴,建立直角坐标系.K那么焦点F的坐标为设|KF|=p(p>0),准线l上的方程为设M(x, y)点M到l的距离为d由定义可得抛物线就是点的集合第三步 列式第四步 代坐标第五步 化简得抛物线的标准方程即:yxO(x,y)K其中p表示焦点到准线的距离.我们通过图象可知,这个抛物线的标准方程只表示开口向右的抛物线,那么其它几种开口方向的抛物线方程又是怎样?xyoxyoxyo口诀:
一次项定轴,系数定方向;焦点与方程同号,准线与方程异号. (1)已知抛物线的标准方程是 ,求它的焦点坐标和准线方程;
(2)已知抛物线的焦点是F(0,-2),求它的标准方程. 求下列抛物线的焦点坐标和准线方程:(1)2p=20,故p=10,
焦点在x轴正方向,
焦点(5,0),准线为x=-5(2)2p= ,故p= ,
焦点在y轴正方向,
焦点 ,准线为焦点在x轴负方向,
焦点 ,准线为(3)先化为标准方程
2p= ,故p= ,
(4)先化为标准方程
求下列抛物线的焦点坐标和准线方程:2p=8,故p=4,
焦点在x轴负方向,
焦点(0,-2),准线为y=2 根据下列条件写出抛物线的
标准方程:(1)焦点是F(3,0);(2)准线方程是x=-1/4;(3)焦点到准线的距离是2. 一种卫星接收天线的轴截面如图所示.卫星波束呈近似平行状态射入轴截面为抛物线的接收天线,经反射聚集到焦点处.已知接收天线的口径为4.8m,深度为0.5m,求抛物线的标准方程和焦点坐标.oyxABF解:如图,建立直角坐标系,设抛物线的标准方程是
y2=2px(p>0).易知A (0.5,2.4),代入方程得p=5.76.2.42=2p×0.5所以,所求抛物线为y2=11.52x,
焦点坐标为(2.88,0).抛物线的定义抛物线的标准方程课后再做好复习巩固.
谢谢!再见!
