6.4 整式的加减 课件(共17张PPT)青岛版数学七年级上册
文档属性
| 名称 | 6.4 整式的加减 课件(共17张PPT)青岛版数学七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 454.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-04 16:21:09 | ||
图片预览




文档简介
(共17张PPT)
6.4整式的加减
1.能运用去括号、合并同类项进行整式的加减运算。
2.能利用整式的运算化简多项式并求值,体会转化的数学思想。
3.在学习活动中学会与他人合作交流的能力。
目标导航
自主学习
请同学们用3分钟的时间,认真学习课本第146页例1的内容, 注意:
1.在列整式的加减算式时,如果整式是多项式,应特别注意什么问题呢?
2.列出算式后,又如何进行的整式加减的运算?
3分钟后检测,比比谁的学习效果好!
例1、(1)求整式 与 的 和
(2)求整式 减
所得的差
即时检测
1求3x2-6x+5与4x2-7x-6的和。
2求2x2+xy+3y2与x2-xy+2y2的差。
(3x2-6x+5)+(4x2-7x-6)
= 3x2-6x+5+4x2-7x-6
=7x2-13x-1
(2x2+xy+3y2) -(x2-xy+2y2)
= 2x2+xy+3y2-x2+xy-2y2
=x2+2xy+y2
结论:
几个整式的加减,通常用括号把每一个整式括起来再用加减号连接
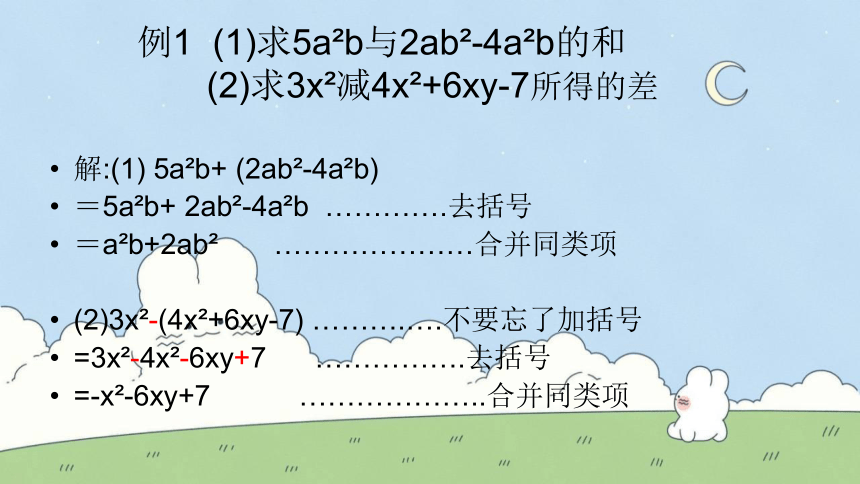
例1 (1)求5a b与2ab -4a b的和
(2)求3x 减4x +6xy-7所得的差
解:(1) 5a b+ (2ab -4a b)
=5a b+ 2ab -4a b ………….去括号
=a b+2ab …………………合并同类项
(2)3x -(4x +6xy-7) ……….….不要忘了加括号
=3x -4x -6xy+7 …………….去括号
=-x -6xy+7 ………………..合并同类项
例2 :化简:(-a -6a)+5a -(a -10a)
解:
(-a -6a)+5a -(a -10a)
=-a -6a+5a -a +10a
=-2a +5a +4a
观察例1,例2 ,
我们在整式加减化简时的步骤是什么
结论:
先去括号,再合并同类项
新知讲解
例3 做大小两个长方体纸盒,尺寸如下(单位:cm):
长 宽 高
小纸盒 a b c
大纸盒 1.5a 2b 2c
(1)做这两个纸盒共用料多少平方厘米?
解: (1)做这两个纸盒共用料(单位:cm2)
(2ab+2bc+2ca)+ (6ab+8bc+6ca)
=2ab+2bc+2ca+ 6ab+8bc+6ca
=8ab +10bc+8ca.
小纸盒的表面积是
(2ab+2bc+2ca)cm2,
大纸盒的表面积是
(6ab+8bc+6ca) cm2.
新知讲解
例 做大小两个长方体纸盒,尺寸如下(单位:cm):
长 宽 高
小纸盒 a b c
大纸盒 1.5a 2b 2c
(2)做大纸盒比做小纸盒多用料多少平方厘米?
小纸盒的表面积是
(2ab+2bc+2ca)cm2,
大纸盒的表面积是
(6ab+8bc+6ca) cm2.
(2)做大纸盒比做小纸盒多用料(单位: cm2)
(6ab+8bc+6ca)-(2ab+2bc+2ca)
= 6ab+8bc+6ca-2ab -2bc-2ca
=4ab+6bc+4ca.
新知讲解
整式加减解决实际问题的一般步骤:
(1) 根据题意列代数式;
(2)去括号、合并同类项;
(3) 得出最后结果.
应用举例
例2 计算
解:(1)(2x2-3x+1)+(-3x2+5x-7)
=2x2-3x+1-3x2+5x-7
=2x2-3x2-3x+5x+1-7
=-x2+2x-6;
1.整式的加减可以归结为去括号和合并同类项。
2.多项式的加减要把每个多项式添上小括号,多项式的加减可以转化为整式的化简,即归结为去括号和合并同类项,最后结果不一定是单项式。
3.运用整式的加减解决简单的实际问题,要清楚题中涉及的数量关系。
课堂小结
随堂练习
1.化简(4a2+2a+2)-(3a2+3a-4)的结果是( )
A.a2-5a+6 B.a2-5a-4
C.a2-a-4 D.a2-a+6
2.已知一个多项式与4x2+9x的和等于4x2+4x-1,则这个多项式是( )
A.-5x-1 B.5x+1
C.-13x-1 D.13x+1
D
A
解:(1)原式=3k2+10k-1;
(2)原式=-7y-4x-16z2;
3.计算:
(1)(4k +7k) +(-k +3k-1);
(2)(5y+3x-15z )-(12y+7x+z );
(3)7(p3 +p2 -p - 1) -2( p3 +p);
(4) -( +m n+m3 ) -( - m n - m3 )
(3)原式=5p3+7p2-9p-7;
(4)原式=-1.
6.4整式的加减
1.能运用去括号、合并同类项进行整式的加减运算。
2.能利用整式的运算化简多项式并求值,体会转化的数学思想。
3.在学习活动中学会与他人合作交流的能力。
目标导航
自主学习
请同学们用3分钟的时间,认真学习课本第146页例1的内容, 注意:
1.在列整式的加减算式时,如果整式是多项式,应特别注意什么问题呢?
2.列出算式后,又如何进行的整式加减的运算?
3分钟后检测,比比谁的学习效果好!
例1、(1)求整式 与 的 和
(2)求整式 减
所得的差
即时检测
1求3x2-6x+5与4x2-7x-6的和。
2求2x2+xy+3y2与x2-xy+2y2的差。
(3x2-6x+5)+(4x2-7x-6)
= 3x2-6x+5+4x2-7x-6
=7x2-13x-1
(2x2+xy+3y2) -(x2-xy+2y2)
= 2x2+xy+3y2-x2+xy-2y2
=x2+2xy+y2
结论:
几个整式的加减,通常用括号把每一个整式括起来再用加减号连接
例1 (1)求5a b与2ab -4a b的和
(2)求3x 减4x +6xy-7所得的差
解:(1) 5a b+ (2ab -4a b)
=5a b+ 2ab -4a b ………….去括号
=a b+2ab …………………合并同类项
(2)3x -(4x +6xy-7) ……….….不要忘了加括号
=3x -4x -6xy+7 …………….去括号
=-x -6xy+7 ………………..合并同类项
例2 :化简:(-a -6a)+5a -(a -10a)
解:
(-a -6a)+5a -(a -10a)
=-a -6a+5a -a +10a
=-2a +5a +4a
观察例1,例2 ,
我们在整式加减化简时的步骤是什么
结论:
先去括号,再合并同类项
新知讲解
例3 做大小两个长方体纸盒,尺寸如下(单位:cm):
长 宽 高
小纸盒 a b c
大纸盒 1.5a 2b 2c
(1)做这两个纸盒共用料多少平方厘米?
解: (1)做这两个纸盒共用料(单位:cm2)
(2ab+2bc+2ca)+ (6ab+8bc+6ca)
=2ab+2bc+2ca+ 6ab+8bc+6ca
=8ab +10bc+8ca.
小纸盒的表面积是
(2ab+2bc+2ca)cm2,
大纸盒的表面积是
(6ab+8bc+6ca) cm2.
新知讲解
例 做大小两个长方体纸盒,尺寸如下(单位:cm):
长 宽 高
小纸盒 a b c
大纸盒 1.5a 2b 2c
(2)做大纸盒比做小纸盒多用料多少平方厘米?
小纸盒的表面积是
(2ab+2bc+2ca)cm2,
大纸盒的表面积是
(6ab+8bc+6ca) cm2.
(2)做大纸盒比做小纸盒多用料(单位: cm2)
(6ab+8bc+6ca)-(2ab+2bc+2ca)
= 6ab+8bc+6ca-2ab -2bc-2ca
=4ab+6bc+4ca.
新知讲解
整式加减解决实际问题的一般步骤:
(1) 根据题意列代数式;
(2)去括号、合并同类项;
(3) 得出最后结果.
应用举例
例2 计算
解:(1)(2x2-3x+1)+(-3x2+5x-7)
=2x2-3x+1-3x2+5x-7
=2x2-3x2-3x+5x+1-7
=-x2+2x-6;
1.整式的加减可以归结为去括号和合并同类项。
2.多项式的加减要把每个多项式添上小括号,多项式的加减可以转化为整式的化简,即归结为去括号和合并同类项,最后结果不一定是单项式。
3.运用整式的加减解决简单的实际问题,要清楚题中涉及的数量关系。
课堂小结
随堂练习
1.化简(4a2+2a+2)-(3a2+3a-4)的结果是( )
A.a2-5a+6 B.a2-5a-4
C.a2-a-4 D.a2-a+6
2.已知一个多项式与4x2+9x的和等于4x2+4x-1,则这个多项式是( )
A.-5x-1 B.5x+1
C.-13x-1 D.13x+1
D
A
解:(1)原式=3k2+10k-1;
(2)原式=-7y-4x-16z2;
3.计算:
(1)(4k +7k) +(-k +3k-1);
(2)(5y+3x-15z )-(12y+7x+z );
(3)7(p3 +p2 -p - 1) -2( p3 +p);
(4) -( +m n+m3 ) -( - m n - m3 )
(3)原式=5p3+7p2-9p-7;
(4)原式=-1.
同课章节目录
- 第1章 基本的几何图形
- 1.1 我们身边的图形世界
- 1.2 几何图形
- 1.3 线段、射线和直线
- 1.4 线段的比较与作法
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数与绝对值
- 第3章 有理数的运算
- 3.1 有理数的加法与减法
- 3.2 有理数的乘法与除法
- 3.3 有理数的乘方
- 3.4 有理数的混合运算
- 3.5 利用计算器进行有理数的计算
- 第4章 数据的收集整理与描述
- 4.1 普查和抽样调查
- 4.2 简单随机抽样
- 4.3 数据的整理
- 4.4 扇形统计图
- 第5章 代数式与函数的初步认识
- 5.1 用字母表示数
- 5.2 代数式
- 5.3 代数式的值
- 5.4 生活中的常量与变量
- 5.5 函数的初步认识
- 第6章 整式的加减
- 6.1 单项式与多项式
- 6.2 同类项
- 6.3 去括号
- 6.4 整式的加减
- 第7章 一元一次方程
- 7.1 等式的基本性质
- 7.2 一元一次方程
- 7.3 一元一次方程的解法
- 7.4 一元一次方程的应用
