数学人教A版(2019)选择性必修第三册8.1.2相关性系数(共16张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第三册8.1.2相关性系数(共16张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-04 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
8.1.2 样本相关系数
引
01
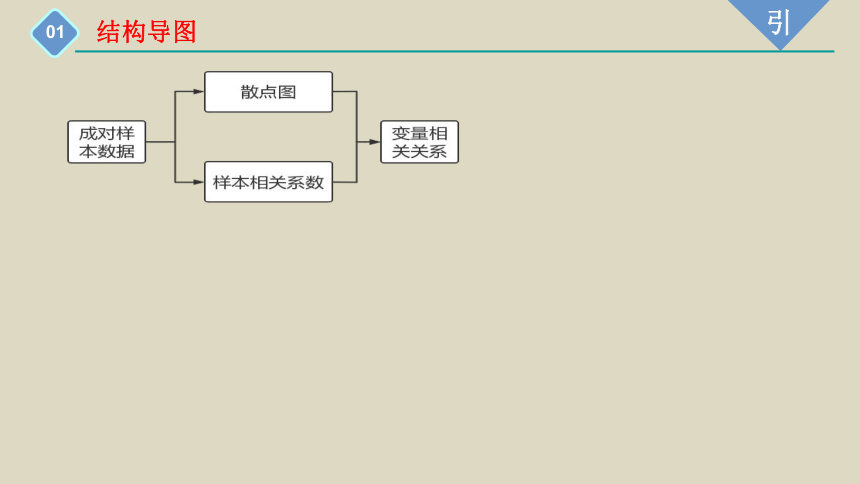
结构导图
引
01
学习目标
1. 结合实例,了解样本相关系数的统计含义,了解样本相关系数与“标准化”处理后的成对数据两分量向量夹角的关系,提升数学抽象核心素养.
2. 结合实例,会通过相关系数比较多组成对数据的相关性. 通过学习样本相关系数,提升数据分析核心素养.
通过观察散点图中成对样本数据的分布规律,我们可以大致推断两个变量是否存在相关系、是正相关还是负相关、是线性相关还是非线性相关等.
评
02
建构新知
散点图优点:虽直观,
缺点:但无法确切地反映成对样本数据的相关程度,也就无法量化两个变量之间相关程度的大小.
提出问题:
引入一个适当的“数字特征”,对成对样本数据的相关程度进行定量分析呢
当r >0时,称成对样本数据正相关;
当r <0时,称成对样本数据负相关.
我们称 r 为变量x和变量y的 样本相关系数.
样本相关系数r 是一个描述成对样本数据的数字特征,它的正负 和绝对值的大小可以反映成对样本数据的变化特征:
1.样本相关系数
评
01
建构新知
样本相关系数r的取值范围为[-1,1]
(有时候也称: 样本相关系数)
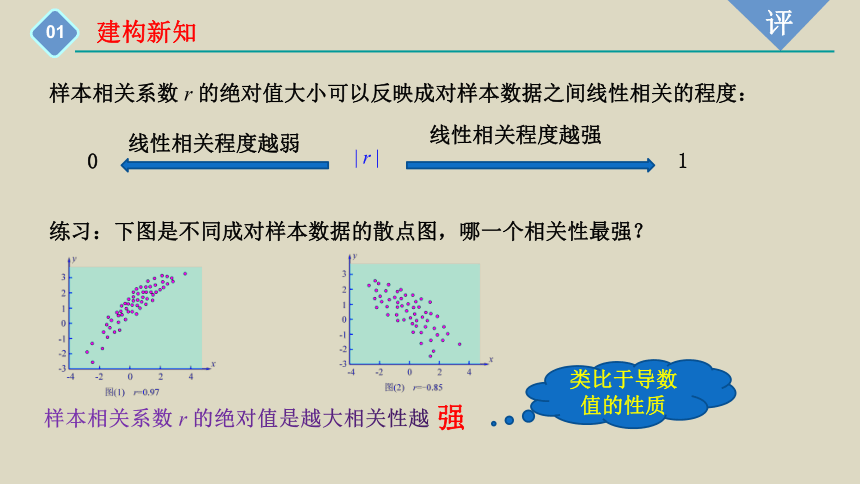
样本相关系数 r 的绝对值大小可以反映成对样本数据之间线性相关的程度:
评
01
建构新知
练习:下图是不同成对样本数据的散点图,哪一个相关性最强?
样本相关系数 r 的绝对值是越大相关性越
强
类比于导数值的性质
线性相关程度越强
0
1
线性相关程度越弱
在实际中,获得总体中所有的成对数据往往是不容易的.因此,我们还是要用样本估计总体的思想来解决问题.也就是说,我们先要通过抽样获取两个变量的一些成对样本数据,再计算出样本相关系数,通过样本相关系数去估计总体相关系数,从而了解两个变量之间的相关程度.对于简单随机样本而言,样本具有随机性,因此样本相关系数r也具有随机性.一般地,样本容量越大,用样本相关系数估计两个变量的相关系数的效果越好.
评
01
建构新知
年龄 23 27 39 41 45 49 50
脂肪 9.5 17.8 21.2 25.9 27.5 26.3 28.2
年龄 53 54 56 57 58 60 61
脂肪 29.6 30.2 31.4 30.8 33.5 35.2 34.6
例1.
根据下表中脂肪含量和年龄的样本数据,推断两个变量是否线性相关, 计算样本相关系数,并推断它们的相关程度(课本).
参考数据:
评
02
巩固应用
解:先画出散点图,如右图所示
观察散点图,可以看出样本点都集中在一条直线附近,由此推断脂肪含量和年龄线性相关.
由样本相关系数 ,可以推断脂肪含量和年龄这两个变量正线性相关,且相关程度很强。脂肪含量与年龄变化趋势相同.
评
02
巩固应用
评
02
巩固应用
练习1: 课本P103的复习巩固第1题。
练习2. 对四组数据进行统计,获得以下散点图,关于其相关系数比较,正确的是( )
A.r2B.r4C.r4D.r2A
追问: 相关系数 r 的值可以为 ± 1吗? 可以是 0 吗?
评
02
巩固应用
请读课本P99
即:当|r| = 1时,样本点(散点)集中于某条直线(都在直线上);
当 r= 0时,成对样本数据间没有线性相关关系,但不排除它们之间有其他相关关系。
二、线性相关系数r的性质
评
01
建构新知
散点集中于一条直线上
(1)当r >0时,称成对样本数据正相关; 当r <0时,称成对样本数据负相关.
样本相关系数 r 可以反映两个随机变量之间的线性相关程度
线性相关程度越强
0
1
线性相关程度越弱
(2)
(3)当|r| = 1时,样本点(散点)集中于某条直线(都在直线上);
(4)当 r= 0时,成对样本数据间没有线性相关关系,但不排除它们之间有其他相关关系。
散点图 成对样本数据的相关性;
样本相关系数 成对样本数据相关的正负性和线性相关程度.
定量
分析
解:
例2.有人收集了某城市居民收入(所有居民在一年内收入的总和)与A商品销售额的10年数据,如下表所示.
第n年 1 2 3 4 5 6 7 8 9 10
居民年收入/亿元 32.2 31.1 32.9 35.8 37.1 38 39 43 44.6 46
A商品销售额/万元 25.0 30.0 34.0 37.0 39.0 41.0 42.0 44.0 48.0 51.0
画出散点图,判断成对样本数据是否线性相关,并通过样本相关系数推断居民年收入与A商品销售额的相关程度和变化趋势的异同.
从散点图看,A商品销售额与居民年收入的样本数据呈现线性相关关系.
居民年收入/亿元
50
45
40
35
20
30
25
30
35
40
45
50
·
·
·
·
·
·
·
55
A商品销售额/万元
·
·
·
评
02
巩固应用
练习2. 有人收集了某城市居民收入(所有居民在一年内收入的总和)与A商品销售额的10年数据,如下表所示.
第n年 1 2 3 4 5 6 7 8 9 10
居民年收入/亿元 32.2 31.1 32.9 35.8 37.1 38 39 43 44.6 46
A商品销售额/万元 25.0 30.0 34.0 37.0 39.0 41.0 42.0 44.0 48.0 51.0
评
02
巩固应用
解:
结
05
课堂小结
1.本节课我们尽力怎样的学习过程?
2.学习了哪些新知识、方法?
1)样本相关系数r
散点图 成对样本数据的相关性;
样本相关系数 成对样本数据相关的正负性和线性相关程度.
定量
分析
结
05
课后练习
1. 某公司为了准确地把握市场,做好产品生产计划,对过去四年的数据进行整理得到了第x年与年销量y(单位:万件)之间的关系如表:
x 1 2 3 4
y 12 28 42 56
在图中画出表中数据的散点图,推断两个变量是否线性相关,计算样本相关系数,并估计它们的相关程度.
附注:参考数据:
8.1.2 样本相关系数
引
01
结构导图
引
01
学习目标
1. 结合实例,了解样本相关系数的统计含义,了解样本相关系数与“标准化”处理后的成对数据两分量向量夹角的关系,提升数学抽象核心素养.
2. 结合实例,会通过相关系数比较多组成对数据的相关性. 通过学习样本相关系数,提升数据分析核心素养.
通过观察散点图中成对样本数据的分布规律,我们可以大致推断两个变量是否存在相关系、是正相关还是负相关、是线性相关还是非线性相关等.
评
02
建构新知
散点图优点:虽直观,
缺点:但无法确切地反映成对样本数据的相关程度,也就无法量化两个变量之间相关程度的大小.
提出问题:
引入一个适当的“数字特征”,对成对样本数据的相关程度进行定量分析呢
当r >0时,称成对样本数据正相关;
当r <0时,称成对样本数据负相关.
我们称 r 为变量x和变量y的 样本相关系数.
样本相关系数r 是一个描述成对样本数据的数字特征,它的正负 和绝对值的大小可以反映成对样本数据的变化特征:
1.样本相关系数
评
01
建构新知
样本相关系数r的取值范围为[-1,1]
(有时候也称: 样本相关系数)
样本相关系数 r 的绝对值大小可以反映成对样本数据之间线性相关的程度:
评
01
建构新知
练习:下图是不同成对样本数据的散点图,哪一个相关性最强?
样本相关系数 r 的绝对值是越大相关性越
强
类比于导数值的性质
线性相关程度越强
0
1
线性相关程度越弱
在实际中,获得总体中所有的成对数据往往是不容易的.因此,我们还是要用样本估计总体的思想来解决问题.也就是说,我们先要通过抽样获取两个变量的一些成对样本数据,再计算出样本相关系数,通过样本相关系数去估计总体相关系数,从而了解两个变量之间的相关程度.对于简单随机样本而言,样本具有随机性,因此样本相关系数r也具有随机性.一般地,样本容量越大,用样本相关系数估计两个变量的相关系数的效果越好.
评
01
建构新知
年龄 23 27 39 41 45 49 50
脂肪 9.5 17.8 21.2 25.9 27.5 26.3 28.2
年龄 53 54 56 57 58 60 61
脂肪 29.6 30.2 31.4 30.8 33.5 35.2 34.6
例1.
根据下表中脂肪含量和年龄的样本数据,推断两个变量是否线性相关, 计算样本相关系数,并推断它们的相关程度(课本).
参考数据:
评
02
巩固应用
解:先画出散点图,如右图所示
观察散点图,可以看出样本点都集中在一条直线附近,由此推断脂肪含量和年龄线性相关.
由样本相关系数 ,可以推断脂肪含量和年龄这两个变量正线性相关,且相关程度很强。脂肪含量与年龄变化趋势相同.
评
02
巩固应用
评
02
巩固应用
练习1: 课本P103的复习巩固第1题。
练习2. 对四组数据进行统计,获得以下散点图,关于其相关系数比较,正确的是( )
A.r2
追问: 相关系数 r 的值可以为 ± 1吗? 可以是 0 吗?
评
02
巩固应用
请读课本P99
即:当|r| = 1时,样本点(散点)集中于某条直线(都在直线上);
当 r= 0时,成对样本数据间没有线性相关关系,但不排除它们之间有其他相关关系。
二、线性相关系数r的性质
评
01
建构新知
散点集中于一条直线上
(1)当r >0时,称成对样本数据正相关; 当r <0时,称成对样本数据负相关.
样本相关系数 r 可以反映两个随机变量之间的线性相关程度
线性相关程度越强
0
1
线性相关程度越弱
(2)
(3)当|r| = 1时,样本点(散点)集中于某条直线(都在直线上);
(4)当 r= 0时,成对样本数据间没有线性相关关系,但不排除它们之间有其他相关关系。
散点图 成对样本数据的相关性;
样本相关系数 成对样本数据相关的正负性和线性相关程度.
定量
分析
解:
例2.有人收集了某城市居民收入(所有居民在一年内收入的总和)与A商品销售额的10年数据,如下表所示.
第n年 1 2 3 4 5 6 7 8 9 10
居民年收入/亿元 32.2 31.1 32.9 35.8 37.1 38 39 43 44.6 46
A商品销售额/万元 25.0 30.0 34.0 37.0 39.0 41.0 42.0 44.0 48.0 51.0
画出散点图,判断成对样本数据是否线性相关,并通过样本相关系数推断居民年收入与A商品销售额的相关程度和变化趋势的异同.
从散点图看,A商品销售额与居民年收入的样本数据呈现线性相关关系.
居民年收入/亿元
50
45
40
35
20
30
25
30
35
40
45
50
·
·
·
·
·
·
·
55
A商品销售额/万元
·
·
·
评
02
巩固应用
练习2. 有人收集了某城市居民收入(所有居民在一年内收入的总和)与A商品销售额的10年数据,如下表所示.
第n年 1 2 3 4 5 6 7 8 9 10
居民年收入/亿元 32.2 31.1 32.9 35.8 37.1 38 39 43 44.6 46
A商品销售额/万元 25.0 30.0 34.0 37.0 39.0 41.0 42.0 44.0 48.0 51.0
评
02
巩固应用
解:
结
05
课堂小结
1.本节课我们尽力怎样的学习过程?
2.学习了哪些新知识、方法?
1)样本相关系数r
散点图 成对样本数据的相关性;
样本相关系数 成对样本数据相关的正负性和线性相关程度.
定量
分析
结
05
课后练习
1. 某公司为了准确地把握市场,做好产品生产计划,对过去四年的数据进行整理得到了第x年与年销量y(单位:万件)之间的关系如表:
x 1 2 3 4
y 12 28 42 56
在图中画出表中数据的散点图,推断两个变量是否线性相关,计算样本相关系数,并估计它们的相关程度.
附注:参考数据:
