数学人教A版(2019)选择性必修第一册1.1.1空间向量及其线性运算(共32张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册1.1.1空间向量及其线性运算(共32张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 53.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-04 18:24:00 | ||
图片预览







文档简介
(共32张PPT)
1.1.1 空间向量及其线性运算
第 一 章空间向量与立体几何
人教A版2019选修第一册
学习目标
1.经历向量及其运算由平面空间推广的过程,了解空间向量
的概念;
2.掌握空间向量的加法、减法、数乘运算及其表示;
3.掌握空间向量加法、减法、数乘的运算律;
4.借助向量的线性运算的学习,提升数学运算素养.
01复习回顾
PART ONE
起点
终点
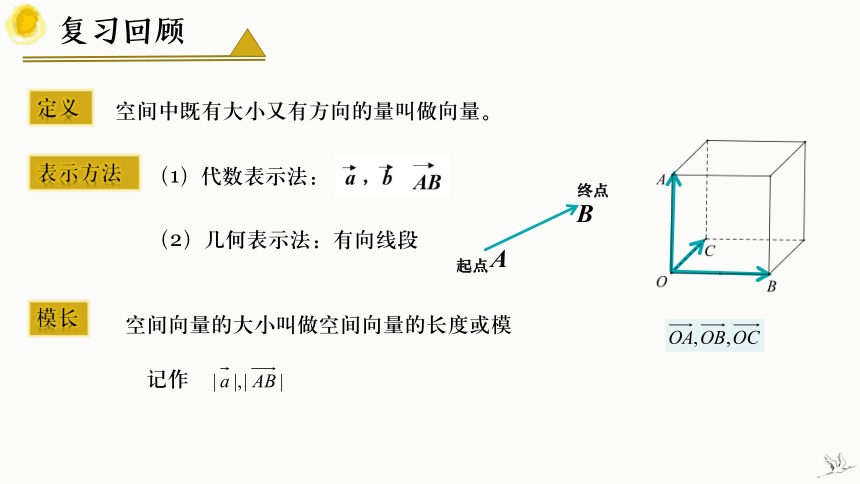
定义
空间中既有大小又有方向的量叫做向量。
模长
记作
表示方法
(2)几何表示法:有向线段
(1)代数表示法:
空间向量的大小叫做空间向量的长度或模
复习回顾
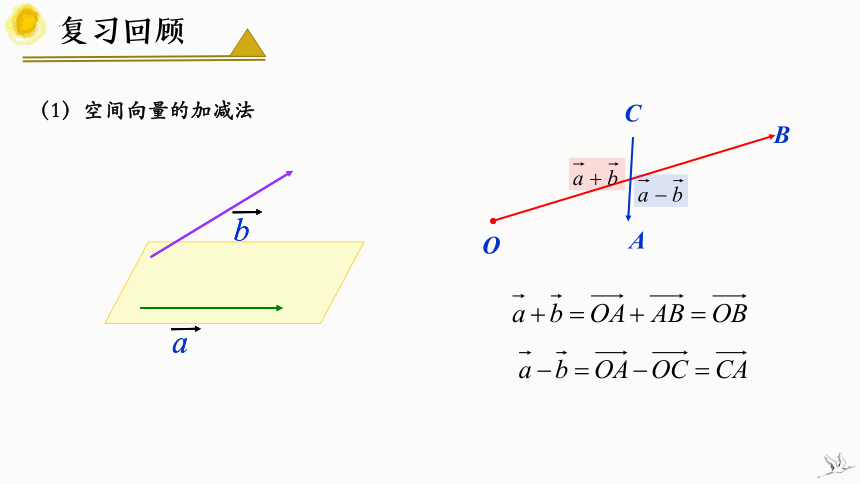
(1)空间向量的加减法
a
b
a
b
O
A
B
C
复习回顾
(2)实数与向量的积
与平面向量一样,实数λ与空间向量a的乘积λa仍然是一个向量,称为向量的数乘运算,记作λa,其长度和方向规定如下:
①|λa|=____.
②当λ>0时,λa与向量a方向相同;当λ<0时,λa与向量a方向 ;当λ=0时,λa=0.
(3)空间向量数乘运算满足以下运算律
①λ(μa)=______; ②λ(a+b)=________;
③(λ1+λ2)a=_________.
相反
|λ||a|
(λμ)a
λa+λb
λ1a+λ2a
复习回顾
02共线向量
PART ONE
共线向量
探究:对任意两个空间向量a,b,如果a=λb(λ∈R),a与b有什么位置关系?反过来,a与b有什么位置关系时,a=λb
类似于平面向量共线的充要条件,对任意两个空间向量a,b(b≠0),a∥b的充要条件是存在实数λ,使a=λb
(1)共线向量:如果表示空间向量的有向线段所在直线互相平行或重合,则这些向量叫做共线向量(或平行向量),
记作
共线向量
(2)共线向量定理
共线向量
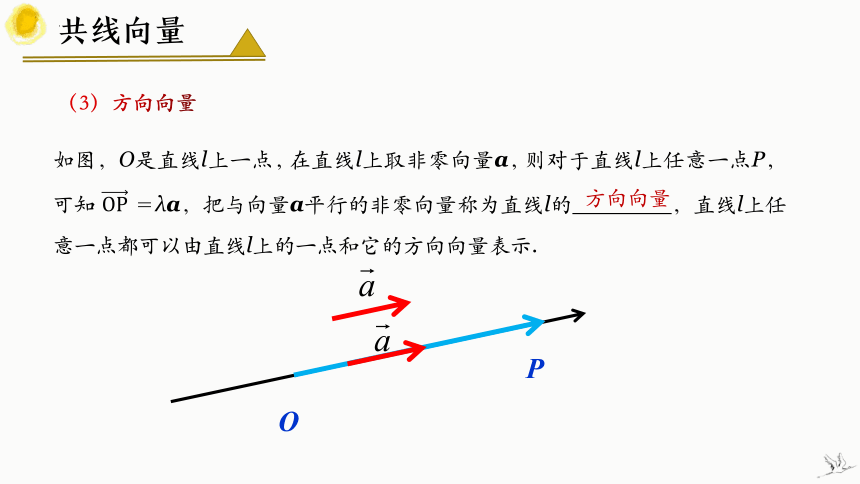
如图,O是直线l上一点,在直线l上取非零向量a,则对于直线l上任意一点P,可知 =λa,把与向量a平行的非零向量称为直线l的 ,直线l上任意一点都可以由直线l上的一点和它的方向向量表示.
(3)方向向量
方向向量
O
P
共线向量
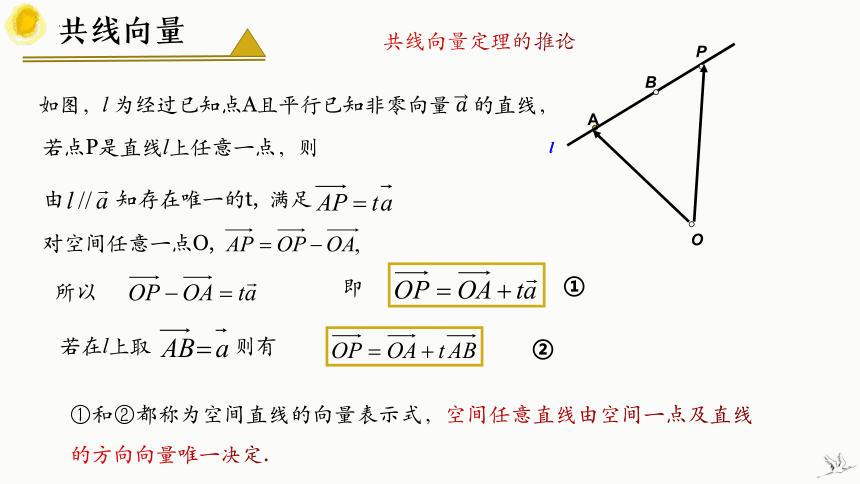
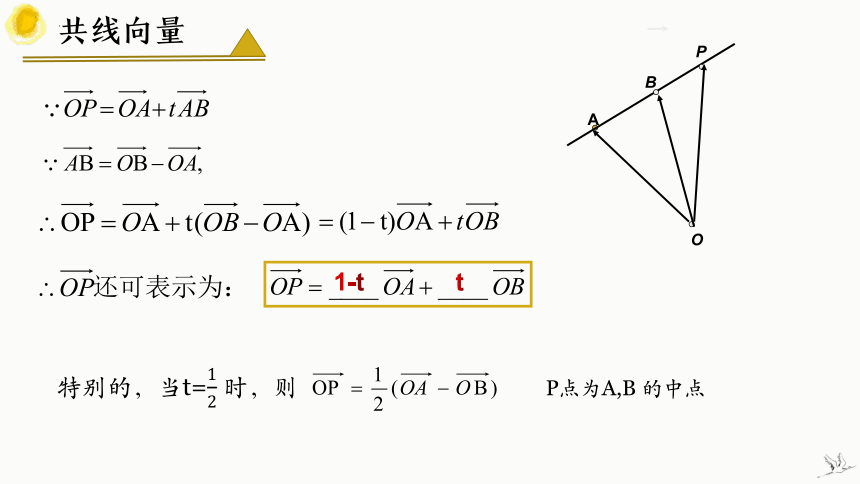
由 知存在唯一的t, 满足
如图,l 为经过已知点A且平行已知非零向量 的直线,
对空间任意一点O,
所以
即
若在l上取 则有
①和②都称为空间直线的向量表示式,空间任意直线由空间一点及直线的方向向量唯一决定.
l
A
B
P
O
若点P是直线l上任意一点,则
①
②
共线向量定理的推论
共线向量
特别的,当t= 时,则
A
B
P
O
t
1-t
P点为A,B 的中点
共线向量
A、B、P三点共线
总结
共线向量
-8
共线向量
2.如图,在正方体ABCD-A1B1C1D1中,E在A1D1上,且,F在对角线A1C上,且 ,求证:E,F,B三点共线.
解:设a,=b,=c,
∵ ,,∴ ,,而==b
∴=b,==.
∴ ,又 ,
∴ = ,即E,F,B三点共线.
共线向量
反思感悟 向量共线的判定及应用
(1)判断或证明两向量a,b(b≠0)共线,就是寻找实数λ,
使a=λb成立,为此常结合题目图形,运用空间向量的
线性运算法则将目标向量化简或用同一组向量表达.
(2)判断或证明空间中的三点(如P,A,B)共线的方法:是否
存在实数λ,
03共面向量
PART ONE
共面向量
1.共面向量:平行于同一平面的向量,叫做共面向量.
共面向量
思考:空间任意两个向量是共面向量,则空间任意三个向量是否共面?
不一定,如图所示,空间中的三个向量不共面.
共面向量
探究1:如果空间向量p与两个不共线向量a,b共面,那么可将三个向量平移到一个平面内,则有p=xa+yb
共面向量
探究2:对空间两个不共线向量a,b共面,有p=xa+yb , 那么向量p与向量a,b有什么位置关系?
C
∵xa,yb分别与a,b共线
∴xa,yb都在a,b确定的平面内, 且平行四边形也在a,b确定的平面内
∴p=xa+yb在a,b确定的平面内。
共面向量
三个向量共面的充要条件:向量p与不共线向量a,b共面的充要条件是存在_____的有序实数对(x,y)__________
共面向量定理
唯一
p=xa+yb
推论:若已知点P在平面ABC内,则有=+y或
=x+y+z(x+y+z=1)
共面向量
P与A、B、C共面
总结
共面向量
1.(多选)对空间任一点O和不共线的三点A,B,C,能得到
P,A,B,C四点共面的是( )
BC
共面向量
共面向量
3.(多选)下列条件中,使M与A,B,C一定共面的是( )
解析 A选项中,3-1-1=1,四点共面,
∴点M,A,B,C共面.
AC
共面向量
且M,A,B,C四点共面,
√
共面向量
5. 如图,已知平行四边形ABCD,从平面AC外一点O作射线OA,OB,OC,OD,在四条射线上分别取点E,F,G,H,使
证明:四点E,F,G,H共面
四点共面→有公共起点的三个向量共面
尝试用空间向量解决立体几何问题
共面向量
证明:
·
方法总结
选择恰当的向量表示问题中的几何元素
通过向量运算得出几何元素的关系
把运算结果“翻译”成相应的几何意义
共面向量
04 课堂小结
PART ONE
1、空间向量的定义及表示方法
2、特殊的向量
3、向量的加减法
4、向量的数乘运算
课堂小结
1.1.1 空间向量及其线性运算
第 一 章空间向量与立体几何
人教A版2019选修第一册
学习目标
1.经历向量及其运算由平面空间推广的过程,了解空间向量
的概念;
2.掌握空间向量的加法、减法、数乘运算及其表示;
3.掌握空间向量加法、减法、数乘的运算律;
4.借助向量的线性运算的学习,提升数学运算素养.
01复习回顾
PART ONE
起点
终点
定义
空间中既有大小又有方向的量叫做向量。
模长
记作
表示方法
(2)几何表示法:有向线段
(1)代数表示法:
空间向量的大小叫做空间向量的长度或模
复习回顾
(1)空间向量的加减法
a
b
a
b
O
A
B
C
复习回顾
(2)实数与向量的积
与平面向量一样,实数λ与空间向量a的乘积λa仍然是一个向量,称为向量的数乘运算,记作λa,其长度和方向规定如下:
①|λa|=____.
②当λ>0时,λa与向量a方向相同;当λ<0时,λa与向量a方向 ;当λ=0时,λa=0.
(3)空间向量数乘运算满足以下运算律
①λ(μa)=______; ②λ(a+b)=________;
③(λ1+λ2)a=_________.
相反
|λ||a|
(λμ)a
λa+λb
λ1a+λ2a
复习回顾
02共线向量
PART ONE
共线向量
探究:对任意两个空间向量a,b,如果a=λb(λ∈R),a与b有什么位置关系?反过来,a与b有什么位置关系时,a=λb
类似于平面向量共线的充要条件,对任意两个空间向量a,b(b≠0),a∥b的充要条件是存在实数λ,使a=λb
(1)共线向量:如果表示空间向量的有向线段所在直线互相平行或重合,则这些向量叫做共线向量(或平行向量),
记作
共线向量
(2)共线向量定理
共线向量
如图,O是直线l上一点,在直线l上取非零向量a,则对于直线l上任意一点P,可知 =λa,把与向量a平行的非零向量称为直线l的 ,直线l上任意一点都可以由直线l上的一点和它的方向向量表示.
(3)方向向量
方向向量
O
P
共线向量
由 知存在唯一的t, 满足
如图,l 为经过已知点A且平行已知非零向量 的直线,
对空间任意一点O,
所以
即
若在l上取 则有
①和②都称为空间直线的向量表示式,空间任意直线由空间一点及直线的方向向量唯一决定.
l
A
B
P
O
若点P是直线l上任意一点,则
①
②
共线向量定理的推论
共线向量
特别的,当t= 时,则
A
B
P
O
t
1-t
P点为A,B 的中点
共线向量
A、B、P三点共线
总结
共线向量
-8
共线向量
2.如图,在正方体ABCD-A1B1C1D1中,E在A1D1上,且,F在对角线A1C上,且 ,求证:E,F,B三点共线.
解:设a,=b,=c,
∵ ,,∴ ,,而==b
∴=b,==.
∴ ,又 ,
∴ = ,即E,F,B三点共线.
共线向量
反思感悟 向量共线的判定及应用
(1)判断或证明两向量a,b(b≠0)共线,就是寻找实数λ,
使a=λb成立,为此常结合题目图形,运用空间向量的
线性运算法则将目标向量化简或用同一组向量表达.
(2)判断或证明空间中的三点(如P,A,B)共线的方法:是否
存在实数λ,
03共面向量
PART ONE
共面向量
1.共面向量:平行于同一平面的向量,叫做共面向量.
共面向量
思考:空间任意两个向量是共面向量,则空间任意三个向量是否共面?
不一定,如图所示,空间中的三个向量不共面.
共面向量
探究1:如果空间向量p与两个不共线向量a,b共面,那么可将三个向量平移到一个平面内,则有p=xa+yb
共面向量
探究2:对空间两个不共线向量a,b共面,有p=xa+yb , 那么向量p与向量a,b有什么位置关系?
C
∵xa,yb分别与a,b共线
∴xa,yb都在a,b确定的平面内, 且平行四边形也在a,b确定的平面内
∴p=xa+yb在a,b确定的平面内。
共面向量
三个向量共面的充要条件:向量p与不共线向量a,b共面的充要条件是存在_____的有序实数对(x,y)__________
共面向量定理
唯一
p=xa+yb
推论:若已知点P在平面ABC内,则有=+y或
=x+y+z(x+y+z=1)
共面向量
P与A、B、C共面
总结
共面向量
1.(多选)对空间任一点O和不共线的三点A,B,C,能得到
P,A,B,C四点共面的是( )
BC
共面向量
共面向量
3.(多选)下列条件中,使M与A,B,C一定共面的是( )
解析 A选项中,3-1-1=1,四点共面,
∴点M,A,B,C共面.
AC
共面向量
且M,A,B,C四点共面,
√
共面向量
5. 如图,已知平行四边形ABCD,从平面AC外一点O作射线OA,OB,OC,OD,在四条射线上分别取点E,F,G,H,使
证明:四点E,F,G,H共面
四点共面→有公共起点的三个向量共面
尝试用空间向量解决立体几何问题
共面向量
证明:
·
方法总结
选择恰当的向量表示问题中的几何元素
通过向量运算得出几何元素的关系
把运算结果“翻译”成相应的几何意义
共面向量
04 课堂小结
PART ONE
1、空间向量的定义及表示方法
2、特殊的向量
3、向量的加减法
4、向量的数乘运算
课堂小结
