2.1 认识无理数 课件(共25张PPT)
文档属性
| 名称 | 2.1 认识无理数 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 664.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-05 00:00:00 | ||
图片预览






文档简介
北师大版 数学 八年级上册
第二章 实数
1 认识无理数
学习目标
1.知道非有理数的存在,认识无理数.
2.理解无理数的概念,掌握无理数与有理数的区别,并能判断一个数是有理数还是无理数.(重点)
3.探索无理数是无限不循环小数,并从中体会无限逼近的思想(难点)
复习回顾
1. 数和 数统称为有理数.
整数分为 ;
分数分为 .
2.一个整数的平方一定是整数吗?
3 .一个分数的平方一定是分数吗?
整
分
正整数、0、负整数
正分数、负分数
是
是
一、创设情境,引入新知
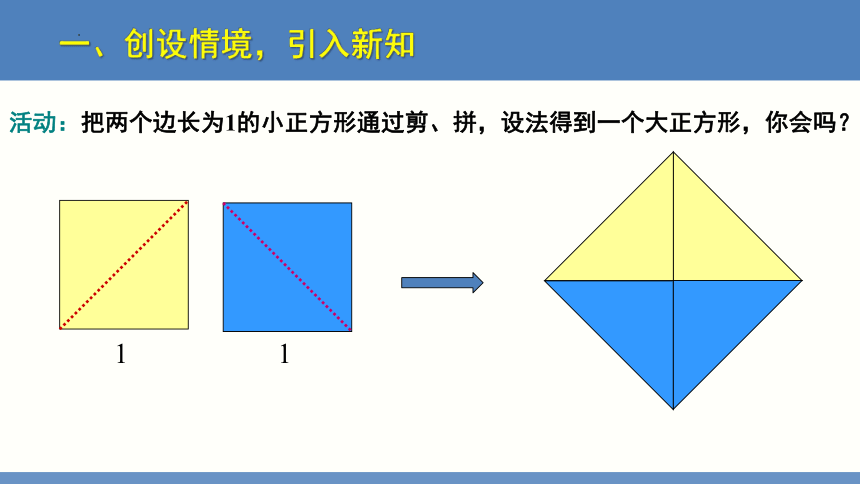
活动:把两个边长为1的小正方形通过剪、拼,设法得到一个大正方形,你会吗?
1
1
一、创设情境,引入新知
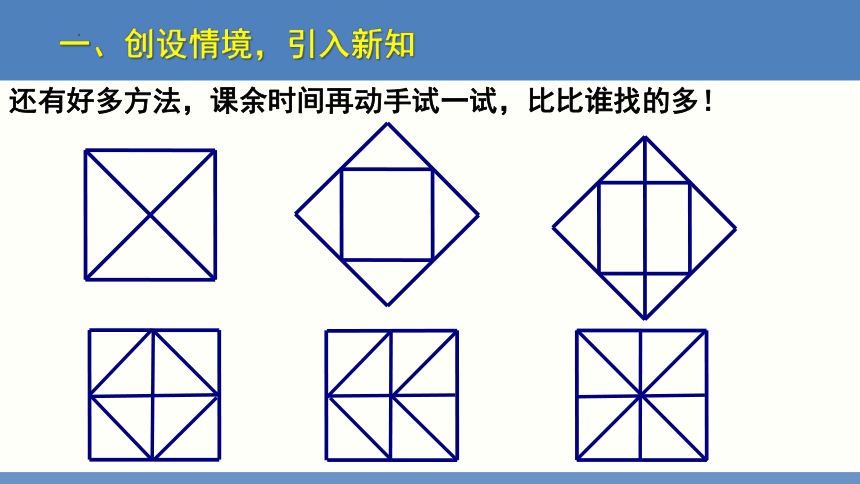
还有好多方法,课余时间再动手试一试,比比谁找的多!
二、自主合作,探究新知
(2)a是一个什么样的数?a可能是整数吗?说说你的理由。
探究一:(1)大正方形的面积是多少呢?如果设大正方形的边长为a,则a满足什么条件?
因为S大正方形=2,所以a2=2.
因为 a2=2, 而12=1, 22=4
所以 12所以 1< a< 2,a不是整数
二、自主合作,探究新知
(3)a可能是分数吗?说说你的理由。并小组内交流。
归纳:a既不是整数,也不是分数;
因为一个整数的平方一定是整数,一个分数的平方一定是分数.
所以a不可能是分数。
归纳:a不是有理数.
探究二:
(1)如图,以直角三角形的斜边为边的正方形的面积是多少?
(2)设该正方形的边长为????,????满足什么条件?
(3)????是有理数吗?
?
2
1
b
(1)利用勾股定理容易求出正方形的面积为5.
二、自主合作,探究新知
(2)b2=5
(3)因为b2=5,而22=4,32=9
所以22<b2<32,
所以2<b<3,
所以b既不是整数,也不是分数。b不是有理数.
二、自主合作,探究新知
上边探究的两个问题中,数a,b确实存在,但都不是有理数。
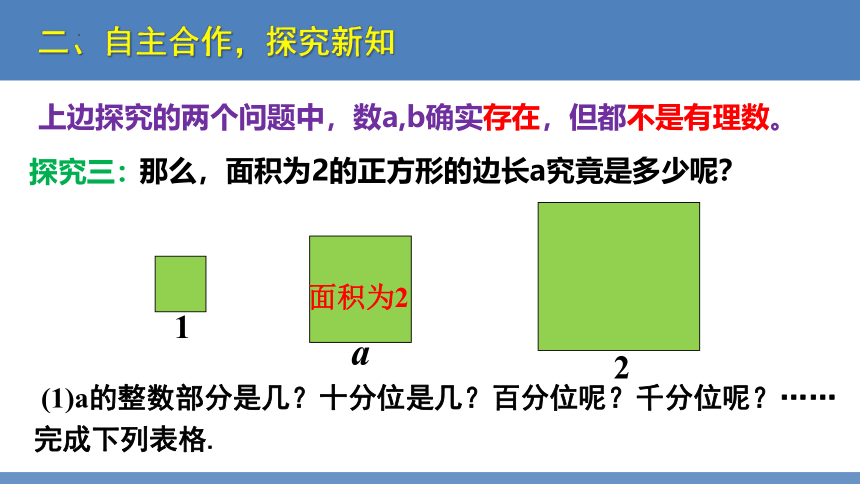
(1)a的整数部分是几?十分位是几?百分位呢?千分位呢?……完成下列表格.
2
探究三:
那么,面积为2的正方形的边长a究竟是多少呢?
1
a
面积为2
二、自主合作,探究新知
请同学们借助计算器进行探索
边长a
面积S=a2
11.961.988 11.999 3961.999 961 641.41.411.4141.414 211.52=2.25
1.42=1.96
1.412=1.9881
1.422=2.0164
1.432=2.0449
1.442=2.0736
1.452=2.1025
1.4152=2.002225
1.4142=1.999396
二、自主合作,探究新知
想一想:还可以继续算下去吗?a可能是有限小数吗?
这种无限逼近求一个数的近似值的方法,我们称为“夹逼法”.
借助计算器,我们可以无限的计算下去,a=1.414 213 56…,
所以a不是一个有限小数,它是一个无限不循环小数.
我们可以根据a的精确度的要求,取不同的近似值:
????≈????.????
?
(结果精确到0.1)
????≈????.????????
?
(结果精确到0.01)
????≈????.????????????
?
(结果精确到0.001)
二、自主合作,探究新知
(1)估计面积为5的正方形的边长b的值(结果精确到0.1),并用计算器验证你的估计。
(2)如果精确到0.01呢?
做一做
b≈2.2
b=2.236067978…,它也是一个无限不循环小数。
b≈2.24
同样,对于体积为2的正方体,借助计算器,可以得到它的棱长c=1.25992105…,它也是一个无限不循环小数。
二、自主合作,探究新知
把下列各数表示成小数,你发现了什么?
探究四:
????,????????,????????,?????????????,????????????.
?
归纳:有理数总可以用有限小数或无限循环小数表示.反过来,任何有限小数或无限不循环小数也都是有理数。
补充:所有的有理数都可以写成两个整数之比,而无理数不能。
????=????.????;????????=????.????;????????=????.????;?????????????=?????.????????;????????????=????.????????
?
.
二、自主合作,探究新知
无理数的定义:
无限不循环小数称为无理数.
除了像上面所述的数a,b,c是无理数外,我们十分熟悉的圆周率????=3.14159265… 也是一个无限不循环小数,因此它也是一个无理数.再如0.5 85 885 8885 88885…(相邻两个5之间8的个数逐次增加1),也是无理数。
?
知识要点
二、自主合作,探究新知
无理数有很多,常见的有以下形式:
①一般的无限不循环小数;
②π及含有π的式子表示的数;
③有规律的无限不循环小数,比如0.1010010001??????(每两个1之间依次增加一个0)
④开方开不尽的数(后边会学习);
?
想一想:你能找到其他的无理数吗?
二、自主合作,探究新知
典例精析
例1:下列各数中,哪些是有理数?哪些是无理数?
3.14,- ,0.57,0.1010001000001…(相邻两个1之间0的个数逐次加2).
. .
解:有理数有:3.14, , 0.57;
. .
无理数有:0.1010001000001…(相邻两个1之间0的个数逐次加2).
二、自主合作,探究新知
例2:在下列正方形网格中,先找出长度为有理数的线段,再找出长度是无理数的线段.
长度为有理数的线段: AB、EF
长度为无理数的线段:CD、GH、MN
三、即学即练,应用知识
1.判断下列说法是否正确:
(1)所有无限小数都是无理数; ( )
(2)所有无理数都是无限小数; ( )
(3)有理数都是有限小数; ( )
(4)不是有限小数的不是有理数. ( )
?
?
?
?
三、即学即练,应用知识
2.下列各数中,哪些是有理数?哪些是无理数?
0.4583,????.?????,- π,-????????,18.
?
解:有理数有: 0.4583,????.?????, -????????,18 ;
无理数有: - π.
?
四、课堂小结
谈谈你本节课有哪些收获?
无限不循环小数称为无理数。
(1)有理数能写成有限小数或无限循环小数,而无理数只能写成无限不循环小数.
(2)所有的有理数都可以写成两个整数之比,而无理数不能。
认识无理数
定义
无理数与有理数的区别
无理数的常见形式
①一般的无限不循环小数;
②π及含有π的式子表示的数;
③有规律的无限不循环小数;
④开方开不尽的数(后边会学习)
五、当堂达标检测
2.一个正方形的面积为10,则它的边长???? ( )
A.是分数 B.是小数 C.是整数 D.无理数
?
D
3.下列数中,是无理数的是 ( )
A.0.3 B.????????? C.0 D.0.333??????
?
B
1.以下各正方形的边长是无理数的是( )
A.面积为25的正方形; B.面积为 的正方形;
C.面积为8的正方形; D.面积为1.44的正方形.
C
4.下列说法正确的个数为( )
①有限小数是有理数; ②无限小数都是无理数;
③无理数都是无限小数; ④有理数是有限小数.
A.1 B.2 C.3 D.4
五、当堂达标检测
B
5.下列方程中,解不是有理数的是( )
A.x2=4 B.2x2-6=0 C.x2+3=12 D.x2=49
D
五、当堂达标检测
6.面积为7的正方形的边长满足的条件是 <边长< (均填整数)。
2 3
7.有六个数:0.123,(-1.5)3,3.1416,????????????,-2π,0.1020020002···(每两个2之间依次增加一个0),若其中无理数的个数为x,整数的个数为y,非负数的个数为z,则x+y+z= .
?
6
五、当堂达标检测
在下图的正方形网格中画出1个三角形使三边都是无理数。
拓展提升
答案不唯一
教材习题2.1-2.2;
六、布置作业
第二章 实数
1 认识无理数
学习目标
1.知道非有理数的存在,认识无理数.
2.理解无理数的概念,掌握无理数与有理数的区别,并能判断一个数是有理数还是无理数.(重点)
3.探索无理数是无限不循环小数,并从中体会无限逼近的思想(难点)
复习回顾
1. 数和 数统称为有理数.
整数分为 ;
分数分为 .
2.一个整数的平方一定是整数吗?
3 .一个分数的平方一定是分数吗?
整
分
正整数、0、负整数
正分数、负分数
是
是
一、创设情境,引入新知
活动:把两个边长为1的小正方形通过剪、拼,设法得到一个大正方形,你会吗?
1
1
一、创设情境,引入新知
还有好多方法,课余时间再动手试一试,比比谁找的多!
二、自主合作,探究新知
(2)a是一个什么样的数?a可能是整数吗?说说你的理由。
探究一:(1)大正方形的面积是多少呢?如果设大正方形的边长为a,则a满足什么条件?
因为S大正方形=2,所以a2=2.
因为 a2=2, 而12=1, 22=4
所以 12
二、自主合作,探究新知
(3)a可能是分数吗?说说你的理由。并小组内交流。
归纳:a既不是整数,也不是分数;
因为一个整数的平方一定是整数,一个分数的平方一定是分数.
所以a不可能是分数。
归纳:a不是有理数.
探究二:
(1)如图,以直角三角形的斜边为边的正方形的面积是多少?
(2)设该正方形的边长为????,????满足什么条件?
(3)????是有理数吗?
?
2
1
b
(1)利用勾股定理容易求出正方形的面积为5.
二、自主合作,探究新知
(2)b2=5
(3)因为b2=5,而22=4,32=9
所以22<b2<32,
所以2<b<3,
所以b既不是整数,也不是分数。b不是有理数.
二、自主合作,探究新知
上边探究的两个问题中,数a,b确实存在,但都不是有理数。
(1)a的整数部分是几?十分位是几?百分位呢?千分位呢?……完成下列表格.
2
探究三:
那么,面积为2的正方形的边长a究竟是多少呢?
1
a
面积为2
二、自主合作,探究新知
请同学们借助计算器进行探索
边长a
面积S=a2
1
1.42=1.96
1.412=1.9881
1.422=2.0164
1.432=2.0449
1.442=2.0736
1.452=2.1025
1.4152=2.002225
1.4142=1.999396
二、自主合作,探究新知
想一想:还可以继续算下去吗?a可能是有限小数吗?
这种无限逼近求一个数的近似值的方法,我们称为“夹逼法”.
借助计算器,我们可以无限的计算下去,a=1.414 213 56…,
所以a不是一个有限小数,它是一个无限不循环小数.
我们可以根据a的精确度的要求,取不同的近似值:
????≈????.????
?
(结果精确到0.1)
????≈????.????????
?
(结果精确到0.01)
????≈????.????????????
?
(结果精确到0.001)
二、自主合作,探究新知
(1)估计面积为5的正方形的边长b的值(结果精确到0.1),并用计算器验证你的估计。
(2)如果精确到0.01呢?
做一做
b≈2.2
b=2.236067978…,它也是一个无限不循环小数。
b≈2.24
同样,对于体积为2的正方体,借助计算器,可以得到它的棱长c=1.25992105…,它也是一个无限不循环小数。
二、自主合作,探究新知
把下列各数表示成小数,你发现了什么?
探究四:
????,????????,????????,?????????????,????????????.
?
归纳:有理数总可以用有限小数或无限循环小数表示.反过来,任何有限小数或无限不循环小数也都是有理数。
补充:所有的有理数都可以写成两个整数之比,而无理数不能。
????=????.????;????????=????.????;????????=????.????;?????????????=?????.????????;????????????=????.????????
?
.
二、自主合作,探究新知
无理数的定义:
无限不循环小数称为无理数.
除了像上面所述的数a,b,c是无理数外,我们十分熟悉的圆周率????=3.14159265… 也是一个无限不循环小数,因此它也是一个无理数.再如0.5 85 885 8885 88885…(相邻两个5之间8的个数逐次增加1),也是无理数。
?
知识要点
二、自主合作,探究新知
无理数有很多,常见的有以下形式:
①一般的无限不循环小数;
②π及含有π的式子表示的数;
③有规律的无限不循环小数,比如0.1010010001??????(每两个1之间依次增加一个0)
④开方开不尽的数(后边会学习);
?
想一想:你能找到其他的无理数吗?
二、自主合作,探究新知
典例精析
例1:下列各数中,哪些是有理数?哪些是无理数?
3.14,- ,0.57,0.1010001000001…(相邻两个1之间0的个数逐次加2).
. .
解:有理数有:3.14, , 0.57;
. .
无理数有:0.1010001000001…(相邻两个1之间0的个数逐次加2).
二、自主合作,探究新知
例2:在下列正方形网格中,先找出长度为有理数的线段,再找出长度是无理数的线段.
长度为有理数的线段: AB、EF
长度为无理数的线段:CD、GH、MN
三、即学即练,应用知识
1.判断下列说法是否正确:
(1)所有无限小数都是无理数; ( )
(2)所有无理数都是无限小数; ( )
(3)有理数都是有限小数; ( )
(4)不是有限小数的不是有理数. ( )
?
?
?
?
三、即学即练,应用知识
2.下列各数中,哪些是有理数?哪些是无理数?
0.4583,????.?????,- π,-????????,18.
?
解:有理数有: 0.4583,????.?????, -????????,18 ;
无理数有: - π.
?
四、课堂小结
谈谈你本节课有哪些收获?
无限不循环小数称为无理数。
(1)有理数能写成有限小数或无限循环小数,而无理数只能写成无限不循环小数.
(2)所有的有理数都可以写成两个整数之比,而无理数不能。
认识无理数
定义
无理数与有理数的区别
无理数的常见形式
①一般的无限不循环小数;
②π及含有π的式子表示的数;
③有规律的无限不循环小数;
④开方开不尽的数(后边会学习)
五、当堂达标检测
2.一个正方形的面积为10,则它的边长???? ( )
A.是分数 B.是小数 C.是整数 D.无理数
?
D
3.下列数中,是无理数的是 ( )
A.0.3 B.????????? C.0 D.0.333??????
?
B
1.以下各正方形的边长是无理数的是( )
A.面积为25的正方形; B.面积为 的正方形;
C.面积为8的正方形; D.面积为1.44的正方形.
C
4.下列说法正确的个数为( )
①有限小数是有理数; ②无限小数都是无理数;
③无理数都是无限小数; ④有理数是有限小数.
A.1 B.2 C.3 D.4
五、当堂达标检测
B
5.下列方程中,解不是有理数的是( )
A.x2=4 B.2x2-6=0 C.x2+3=12 D.x2=49
D
五、当堂达标检测
6.面积为7的正方形的边长满足的条件是 <边长< (均填整数)。
2 3
7.有六个数:0.123,(-1.5)3,3.1416,????????????,-2π,0.1020020002···(每两个2之间依次增加一个0),若其中无理数的个数为x,整数的个数为y,非负数的个数为z,则x+y+z= .
?
6
五、当堂达标检测
在下图的正方形网格中画出1个三角形使三边都是无理数。
拓展提升
答案不唯一
教材习题2.1-2.2;
六、布置作业
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
