数学人教A版(2019)选择性必修第一册1.3.1空间直角坐标系(共24张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册1.3.1空间直角坐标系(共24张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 37.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-04 20:11:41 | ||
图片预览








文档简介
(共24张PPT)
1.3.1 空间直角坐标系
第 一 章空间向量与立体几何
人教A版2019选修第一册
学习目标
1.了解空间直角坐标系,理解空间向量的坐标表示,
2.掌握空间向量运算的坐标表示;
3.掌握空间向量垂直与平行的条件及其应用,
4.掌握空间向量的模夹角以及两点间距离公式,能运用公式解决问题。
01情景导入
PART ONE
情景导入
学习了空间向量基本定理,建立了“空间基底”的概念,我们就可以利用基底表示任意一个空间向量,进而把空间向量的运算转化为基向量的运算.所以,基底概念的引人为几何问题代数化奠定了基础.
在平面向量中,我们以平面直角坐标系中与工轴、y轴方向相同的两个单位向量i,j为基底,建立了向量的坐标与点的坐标的一一对应关系,从而把平面向量的运算化归为数的运算.
平面向量
类似地,为了把空间向量的运算化归为数的运算,能否利用空间向量基本定理和空间的单位正交基底,建立空间直角坐标系,进而建立空间向量的坐标与空间点的坐标的一一对应呢
空间向量
情景导入
我国著名数学家吴文俊先生在《数学教育现代化问题》中指出:“数学研究数量关系与空间形式,简单讲就是形与数,欧几里得几何体系的特点是排除了数量关系,对于研究空间形式,你要真正的‘腾飞’,不通过数量关系,我想不出有什么好的办法…….”
吴文俊先生明确地指出中学几何的“腾飞”是“数量化”,也就是坐标系的引入,使得几何问题“代数化”,为了使得空间几何“代数化”,我们引入了坐标及其运算.
02空间直角坐标系
PART ONE
空间直角坐标系
在空间选定一点O和一个单位正交基底,以点O为原点,分别以i,j,k的方向为正方向、以它们的长为单位长度建立三条数轴:x轴、y轴、z轴,它们都叫做坐标轴.这时我们就建立了一个空间直角坐标系Oxyz,O叫做原点,i,j,k都叫做坐标向量,通过每两个坐标轴的平面叫做坐标平面,分别称为Oxy平面,Oyz平面,Ozx平面.
空间直角坐标系定义
画法
画空间直角坐标系Oxyz时,一般使∠xOy =135°(或45°),∠yOz=90°
空间直角坐标系
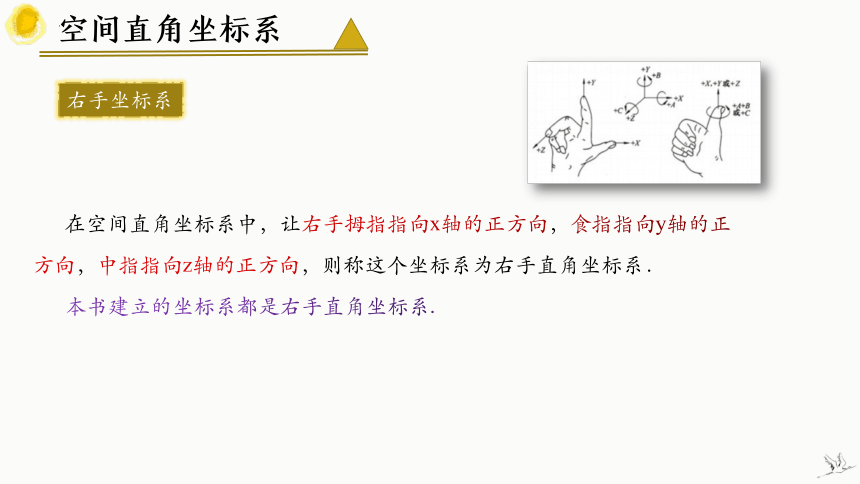
右手坐标系
在空间直角坐标系中,让右手拇指指向x轴的正方向,食指指向y轴的正方向,中指指向z轴的正方向,则称这个坐标系为右手直角坐标系.
本书建立的坐标系都是右手直角坐标系.
空间直角坐标系
问题1:在空间直角坐标系中,坐标平面上的点和坐标轴上的点的坐标有何特征?
1.坐标平面上的点的坐标特征:
xOy平面上的点的竖坐标为0,即(x,y,0).
yOz平面上的点的横坐标为0,即(0,y,z).
xOz平面上的点的纵坐标为0,即(x,0,z).
空间直角坐标系
2.坐标轴上的点的坐标特征:
x轴上的点的纵坐标、竖坐标都为0,即(x,0,0).
y轴上的点的横坐标、竖坐标都为0,即(0,y,0).
z轴上的点的横坐标、纵坐标都为0,即(0,0,z).
问题1:在空间直角坐标系中,坐标平面上的点和坐标轴上的点的坐标有何特征?
03空间点、向量的坐标
PART ONE
空间点、向量的坐标
探究:在平面直角坐标系中,每一个点和向量都可用一对有序实数(即它的坐标)表示.对空间直角坐标系中的每一个点和向量,是否也有类似的表示呢
空间点、向量的坐标
如图,在空间直角坐标系Oxyz中,,,为坐标向量,对空间任意一点A,对应一个向量,且点A的位置由向量唯一确定,由空间向量基本定理,存在唯一的有序实数组(,,),使=++.
在单位正交基底{,,}下与向量对应的有序实数组(,,),叫做点A在空间直角坐标系中的坐标,记作A(,,).其中叫做横坐标,叫做纵坐标,叫做竖坐标.
z
空间点、向量的坐标
1.在长方体ABCD-A1B1C1D1中,AD=3,AB=5,AA1=4,建立适当的坐标系写出此长方体各顶点的坐标.
解:如图,以DA所在直线为x轴,以DC所在直线为y轴,DD1所在直线为z轴建立空间直角坐标系Oxyz.所以D(0,0,0).
因为长方体的棱长AD=3,DC=AB=5,DD1=AA1=4,
可得A(3,0,0),C(0,5,0),D1(0,0,4),B (3,5,0),A1(3,0,4),
C1(0,5,4),B(3,5,0),D1(0,0,4),B1 (3,5,4).
空间点、向量的坐标
1.建立空间直角坐标系时应遵循以下原则:
(1)利用共顶点的互相垂直的三条棱,构建空间直角坐标系;
(2)利用线面垂直关系,构建空间直角坐标系;
(3)利用面面垂直关系,构建空间直角坐标系.
2.求某点的坐标时,一般先找这一点在坐标轴(坐标平面)的射影,确定坐标轴(坐标平面)点的坐标,再找出它在另两个轴上的射影,确定点的坐标.
方法总结
空间点、向量的坐标
2.如图,在长方体ABCD-A1B1C1D1中,|AB|=4,|AD|=3,|AA1|=5,N为棱CC1的中点,分别以AB,AD,AA1所在的直线为x,y,z轴,建立空间直角坐标系.
(1)求点A,B,C,D,A1,B1,C1,D1的坐标;
(2)求点N的坐标.
空间点、向量的坐标
解:(1)显然A(0,0,0),由于点B在x轴的正半轴上,且|OB|=4,所以B(4,0,0).同理,可得D(0,3,0),A1(0,0,5).
由于点C在坐标平面xOy内,BC⊥AB,CD⊥AD,则点C(4,3,0).
同理,可得B1(4,0,5),D1(0,3,5),与点C的坐标相比,点C1的坐标中只有竖坐标与点C不同,CC1=AA1=5,则点C1(4,3,5).
(2)由(1)知,C(4,3,0),C1(4,3,5),则C1C的中点为,即N.
空间点、向量的坐标
在平面直角坐标系中,点P(x,y)的几种特殊的对称点的坐标如下:
(1)关于原点的对称点是P′(-x,-y);
(2)关于x轴的对称点是P″(x,-y);
(3)关于y轴的对称点是P′″ (-x,y),
那么,在空间直角坐标系内,点P(x,y,z)的几种特殊的对称点坐标:
(1)关于原点的对称点是P1______________;
(-x,-y,-z)
空间点、向量的坐标
(2)关于横轴(x轴)的对称点是P2_____________________;
(3)关于纵轴(y轴)的对称点是P3_____________________;
(4)关于竖轴(z轴)的对称点是P4_____________________;
(5)关于xOy坐标平面的对称点是P5__________________;
(6)关于yOz坐标平面的对称点是P6__________________;
(7)关于zOx坐标平面的对称点是P7____________________.
【点拨】 利用数形结合求点的坐标.
(x,-y,-z)
(-x,y,-z)
(-x,-y,z)
(x,y,-z)
(-x,y,z)
(x,-y,z)
记忆方法:“关于谁对称谁不变,其余的相反”,如关于x轴的对称的点,横坐标不变,纵坐标、竖坐标变为原来的相反数;关于xOy坐标平面对称的点,横、纵坐标不变,竖坐标相反.
空间点、向量的坐标
空间点、向量的坐标
1.点P(4,0,1)在空间直角坐标系中的位置是在( )
A.y轴上 B.xOy平面上
C.xOz平面上 D.yOz平面上
C
【解析】 由于点P的纵坐标为0,横坐标与竖坐标都不为0,故该点在xOz平面上.
空间点、向量的坐标
2.在空间直角坐标系中,点P(-2,1,4)关于点M(2,-1,-4)对称的点P′的坐标是( )
A.(0,0,0) B.(2,-1,-4)
C.(6,-3,-12) D.(-2,3,12)
【解析】 根据题意知M为线段PP′的中点,设P′(x,y,z),由中点坐标公式,可得x=2×2-(-2)=6,y=2×(-1)-1=-3,z=2×(-4)-4=-12,所以P′(6,-3,-12).
C
04课堂小结
PART ONE
课堂小结
1.3.1 空间直角坐标系
第 一 章空间向量与立体几何
人教A版2019选修第一册
学习目标
1.了解空间直角坐标系,理解空间向量的坐标表示,
2.掌握空间向量运算的坐标表示;
3.掌握空间向量垂直与平行的条件及其应用,
4.掌握空间向量的模夹角以及两点间距离公式,能运用公式解决问题。
01情景导入
PART ONE
情景导入
学习了空间向量基本定理,建立了“空间基底”的概念,我们就可以利用基底表示任意一个空间向量,进而把空间向量的运算转化为基向量的运算.所以,基底概念的引人为几何问题代数化奠定了基础.
在平面向量中,我们以平面直角坐标系中与工轴、y轴方向相同的两个单位向量i,j为基底,建立了向量的坐标与点的坐标的一一对应关系,从而把平面向量的运算化归为数的运算.
平面向量
类似地,为了把空间向量的运算化归为数的运算,能否利用空间向量基本定理和空间的单位正交基底,建立空间直角坐标系,进而建立空间向量的坐标与空间点的坐标的一一对应呢
空间向量
情景导入
我国著名数学家吴文俊先生在《数学教育现代化问题》中指出:“数学研究数量关系与空间形式,简单讲就是形与数,欧几里得几何体系的特点是排除了数量关系,对于研究空间形式,你要真正的‘腾飞’,不通过数量关系,我想不出有什么好的办法…….”
吴文俊先生明确地指出中学几何的“腾飞”是“数量化”,也就是坐标系的引入,使得几何问题“代数化”,为了使得空间几何“代数化”,我们引入了坐标及其运算.
02空间直角坐标系
PART ONE
空间直角坐标系
在空间选定一点O和一个单位正交基底,以点O为原点,分别以i,j,k的方向为正方向、以它们的长为单位长度建立三条数轴:x轴、y轴、z轴,它们都叫做坐标轴.这时我们就建立了一个空间直角坐标系Oxyz,O叫做原点,i,j,k都叫做坐标向量,通过每两个坐标轴的平面叫做坐标平面,分别称为Oxy平面,Oyz平面,Ozx平面.
空间直角坐标系定义
画法
画空间直角坐标系Oxyz时,一般使∠xOy =135°(或45°),∠yOz=90°
空间直角坐标系
右手坐标系
在空间直角坐标系中,让右手拇指指向x轴的正方向,食指指向y轴的正方向,中指指向z轴的正方向,则称这个坐标系为右手直角坐标系.
本书建立的坐标系都是右手直角坐标系.
空间直角坐标系
问题1:在空间直角坐标系中,坐标平面上的点和坐标轴上的点的坐标有何特征?
1.坐标平面上的点的坐标特征:
xOy平面上的点的竖坐标为0,即(x,y,0).
yOz平面上的点的横坐标为0,即(0,y,z).
xOz平面上的点的纵坐标为0,即(x,0,z).
空间直角坐标系
2.坐标轴上的点的坐标特征:
x轴上的点的纵坐标、竖坐标都为0,即(x,0,0).
y轴上的点的横坐标、竖坐标都为0,即(0,y,0).
z轴上的点的横坐标、纵坐标都为0,即(0,0,z).
问题1:在空间直角坐标系中,坐标平面上的点和坐标轴上的点的坐标有何特征?
03空间点、向量的坐标
PART ONE
空间点、向量的坐标
探究:在平面直角坐标系中,每一个点和向量都可用一对有序实数(即它的坐标)表示.对空间直角坐标系中的每一个点和向量,是否也有类似的表示呢
空间点、向量的坐标
如图,在空间直角坐标系Oxyz中,,,为坐标向量,对空间任意一点A,对应一个向量,且点A的位置由向量唯一确定,由空间向量基本定理,存在唯一的有序实数组(,,),使=++.
在单位正交基底{,,}下与向量对应的有序实数组(,,),叫做点A在空间直角坐标系中的坐标,记作A(,,).其中叫做横坐标,叫做纵坐标,叫做竖坐标.
z
空间点、向量的坐标
1.在长方体ABCD-A1B1C1D1中,AD=3,AB=5,AA1=4,建立适当的坐标系写出此长方体各顶点的坐标.
解:如图,以DA所在直线为x轴,以DC所在直线为y轴,DD1所在直线为z轴建立空间直角坐标系Oxyz.所以D(0,0,0).
因为长方体的棱长AD=3,DC=AB=5,DD1=AA1=4,
可得A(3,0,0),C(0,5,0),D1(0,0,4),B (3,5,0),A1(3,0,4),
C1(0,5,4),B(3,5,0),D1(0,0,4),B1 (3,5,4).
空间点、向量的坐标
1.建立空间直角坐标系时应遵循以下原则:
(1)利用共顶点的互相垂直的三条棱,构建空间直角坐标系;
(2)利用线面垂直关系,构建空间直角坐标系;
(3)利用面面垂直关系,构建空间直角坐标系.
2.求某点的坐标时,一般先找这一点在坐标轴(坐标平面)的射影,确定坐标轴(坐标平面)点的坐标,再找出它在另两个轴上的射影,确定点的坐标.
方法总结
空间点、向量的坐标
2.如图,在长方体ABCD-A1B1C1D1中,|AB|=4,|AD|=3,|AA1|=5,N为棱CC1的中点,分别以AB,AD,AA1所在的直线为x,y,z轴,建立空间直角坐标系.
(1)求点A,B,C,D,A1,B1,C1,D1的坐标;
(2)求点N的坐标.
空间点、向量的坐标
解:(1)显然A(0,0,0),由于点B在x轴的正半轴上,且|OB|=4,所以B(4,0,0).同理,可得D(0,3,0),A1(0,0,5).
由于点C在坐标平面xOy内,BC⊥AB,CD⊥AD,则点C(4,3,0).
同理,可得B1(4,0,5),D1(0,3,5),与点C的坐标相比,点C1的坐标中只有竖坐标与点C不同,CC1=AA1=5,则点C1(4,3,5).
(2)由(1)知,C(4,3,0),C1(4,3,5),则C1C的中点为,即N.
空间点、向量的坐标
在平面直角坐标系中,点P(x,y)的几种特殊的对称点的坐标如下:
(1)关于原点的对称点是P′(-x,-y);
(2)关于x轴的对称点是P″(x,-y);
(3)关于y轴的对称点是P′″ (-x,y),
那么,在空间直角坐标系内,点P(x,y,z)的几种特殊的对称点坐标:
(1)关于原点的对称点是P1______________;
(-x,-y,-z)
空间点、向量的坐标
(2)关于横轴(x轴)的对称点是P2_____________________;
(3)关于纵轴(y轴)的对称点是P3_____________________;
(4)关于竖轴(z轴)的对称点是P4_____________________;
(5)关于xOy坐标平面的对称点是P5__________________;
(6)关于yOz坐标平面的对称点是P6__________________;
(7)关于zOx坐标平面的对称点是P7____________________.
【点拨】 利用数形结合求点的坐标.
(x,-y,-z)
(-x,y,-z)
(-x,-y,z)
(x,y,-z)
(-x,y,z)
(x,-y,z)
记忆方法:“关于谁对称谁不变,其余的相反”,如关于x轴的对称的点,横坐标不变,纵坐标、竖坐标变为原来的相反数;关于xOy坐标平面对称的点,横、纵坐标不变,竖坐标相反.
空间点、向量的坐标
空间点、向量的坐标
1.点P(4,0,1)在空间直角坐标系中的位置是在( )
A.y轴上 B.xOy平面上
C.xOz平面上 D.yOz平面上
C
【解析】 由于点P的纵坐标为0,横坐标与竖坐标都不为0,故该点在xOz平面上.
空间点、向量的坐标
2.在空间直角坐标系中,点P(-2,1,4)关于点M(2,-1,-4)对称的点P′的坐标是( )
A.(0,0,0) B.(2,-1,-4)
C.(6,-3,-12) D.(-2,3,12)
【解析】 根据题意知M为线段PP′的中点,设P′(x,y,z),由中点坐标公式,可得x=2×2-(-2)=6,y=2×(-1)-1=-3,z=2×(-4)-4=-12,所以P′(6,-3,-12).
C
04课堂小结
PART ONE
课堂小结
