数学人教A版(2019)选择性必修第一册1.4.1用空间向量研究直线、平面的位置关系(共22张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册1.4.1用空间向量研究直线、平面的位置关系(共22张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-04 21:09:13 | ||
图片预览






文档简介
(共22张PPT)
1.4.1
用空间向量研究直线、平面的位置关系
01
空间中点、线、面的向量表示
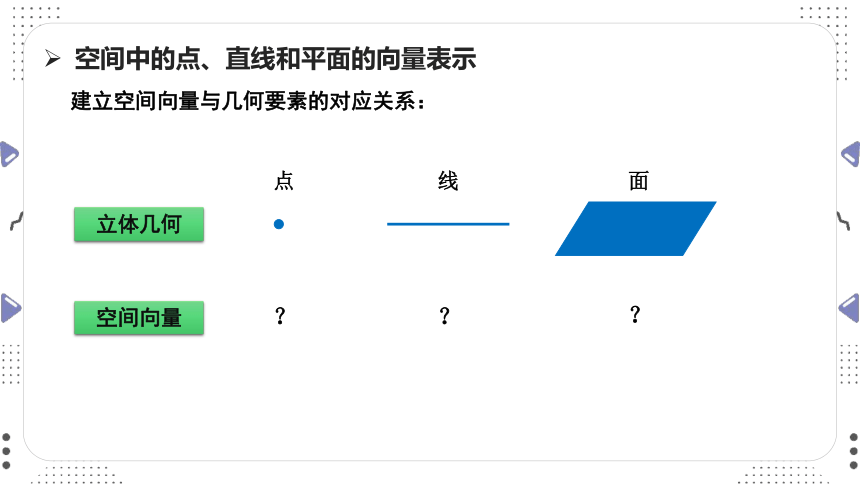
空间中的点、直线和平面的向量表示
立体几何
点
线
面
空间向量
?
?
?
建立空间向量与几何要素的对应关系:
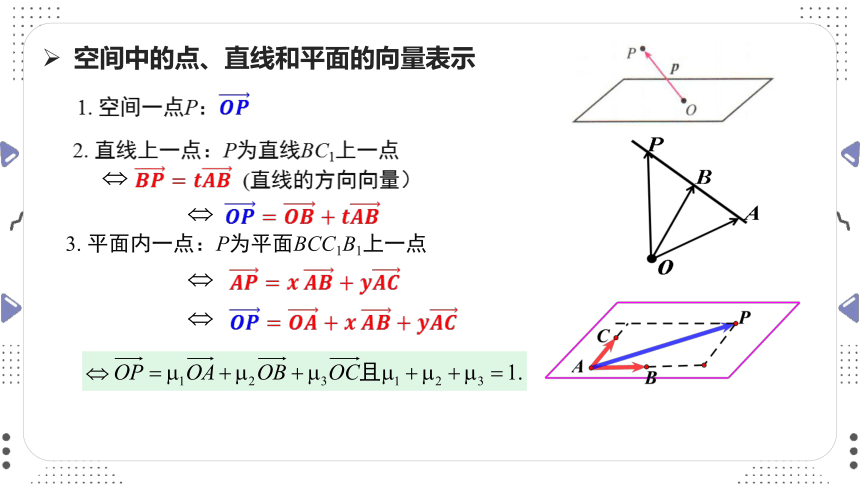
2. 直线上一点:P为直线BC1
(直线的方向向量)
3. 平面内一点:P为平面BCC1B1上一点
1. 空间一点P:
空间中的点、直线和平面的向量表示
典例分析:直线的方向向量求解
D
空间中的点、直线和平面的向量表示
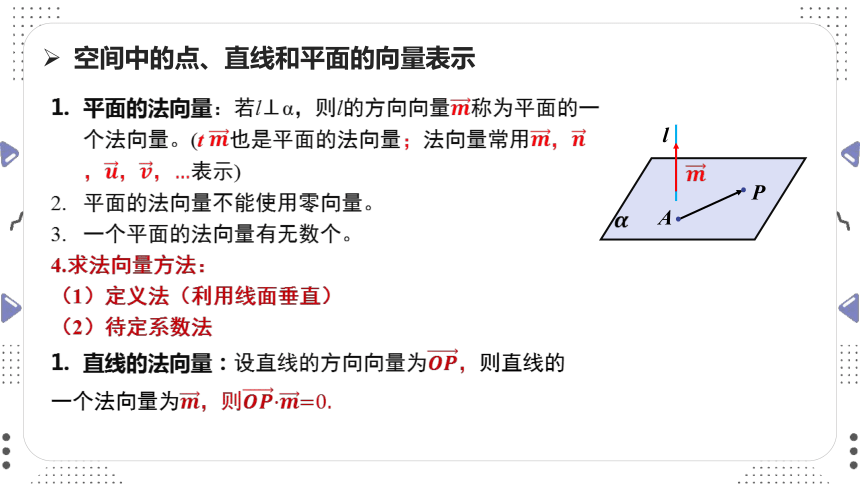
平面的法向量:若l⊥α,则l的方向向量称为平面的一个法向量。(t 也是平面的法向量;法向量常用,,,…表示)
平面的法向量不能使用零向量。
一个平面的法向量有无数个。
4.求法向量方法:
(1)定义法(利用线面垂直)
(2)待定系数法
直线的法向量:设直线的方向向量为,则直线的
一个法向量为,则·=0.
l
A
P
典例分析:平面的法向量求解
例1.已知长方体ABCD-A1B1C1D1中,AB=4,BC=3,CC1 =2,M为AB中点.以D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴,建立如图所示空间直角坐标系,
(1)定义法:求平面BCC1B1的一个法向量.
(2)待定系数法:求平面MCA1的一个法向量.
设法向量
列方程组
赋非零值
建系描点
巩固训练:平面的法向量求解
(1)平面ABCD; (2)平面ACC1A1;
02
空间中直线和平面的平行
空间中平行和垂直关系的向量表示
用直线的方向向量、平面的法向量来刻画直线、平面的平行关系。
l1
l2
设,是l1,l2,l的方向向量,是平面α,β的法向量,
l
向量法证明线线平行
向量法证明线线平行
【例2】棱长为2的平行六面体ABCD-A1B1C1D1中,
(1)若点E,F分别是AB,D1C1的中点,求证:CF∥A1E.(基底法)
x
y
z
基底法
坐标法
【例】棱长为2的正方体ABCD-A1B1C1D1中,
(2)若点M,N分别是BC1,CC1的中点,求证:MN∥平面A1BD.
向量法证明线面平行
x
y
z
向量法证明面面平行
【例】棱长为2的正方体ABCD-A1B1C1D1中,
(3)若点G,K分别是DD1,CC1的中点,O为底面ABCD的中心,
求证:平面GHA∥平面D1BK.
x
y
z
x
y
z
P30-例3.长方体ABCD-A1B1C1D1中,AB=4,BC=3,CC1=2,
线段B1C上是否存在点P,使得A1P∥平面ACD1.
平行中的动点问题
总结:直线、平行的平行问题
1.证线线平行:
①证平行四边形得对边平行;
②中位线;
③对应线段成比例;
④平行线的传递性;
⑤线面平行的定义
⑥两直线的方向向量共线(直接法/基底法/坐标法找λ)
2.证线面平行:
①线面平行的判定定理:几何法、基底法、坐标法
平面外的直线l与平面α内的一条直线平行,则l//α.
②法向量坐标法:直线的方向向量与平面的法向量垂直
③直线的方向向量与平面内两个不共线的向量共面.
3.证面面平行:
①面面平行的判定定理:几何法、基底法、坐标法
平面α内的两条相交直线均平行于平面β,则α//β.
②法向量坐标法:两平面的法向量共线
03
空间中直线和平面的垂直
设,是l1,l2,l的方向向量,是平面α,β的法向量,
空间中直线、平面垂直的向量表示
l1
l2
l
P20-例2. 如图所示,在正方体ABCD –A1B1C1D1中,E, F分别是BB1, D1B1的中点,求证:EF⊥DA1.
A
D
C
B
A1
D1
C1
B1
E
F
点的坐标
向量的坐标
向量的
坐标运算
几何
关系
翻译
建系
x
y
z
例题;棱长为2的正方体ABCD-A1B1C1D1中,E,F,M分别为棱AB,BC,B1B的中点,求证:D1M⊥平面B1EF.
向量法证线线垂直
1.4.1
用空间向量研究直线、平面的位置关系
01
空间中点、线、面的向量表示
空间中的点、直线和平面的向量表示
立体几何
点
线
面
空间向量
?
?
?
建立空间向量与几何要素的对应关系:
2. 直线上一点:P为直线BC1
(直线的方向向量)
3. 平面内一点:P为平面BCC1B1上一点
1. 空间一点P:
空间中的点、直线和平面的向量表示
典例分析:直线的方向向量求解
D
空间中的点、直线和平面的向量表示
平面的法向量:若l⊥α,则l的方向向量称为平面的一个法向量。(t 也是平面的法向量;法向量常用,,,…表示)
平面的法向量不能使用零向量。
一个平面的法向量有无数个。
4.求法向量方法:
(1)定义法(利用线面垂直)
(2)待定系数法
直线的法向量:设直线的方向向量为,则直线的
一个法向量为,则·=0.
l
A
P
典例分析:平面的法向量求解
例1.已知长方体ABCD-A1B1C1D1中,AB=4,BC=3,CC1 =2,M为AB中点.以D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴,建立如图所示空间直角坐标系,
(1)定义法:求平面BCC1B1的一个法向量.
(2)待定系数法:求平面MCA1的一个法向量.
设法向量
列方程组
赋非零值
建系描点
巩固训练:平面的法向量求解
(1)平面ABCD; (2)平面ACC1A1;
02
空间中直线和平面的平行
空间中平行和垂直关系的向量表示
用直线的方向向量、平面的法向量来刻画直线、平面的平行关系。
l1
l2
设,是l1,l2,l的方向向量,是平面α,β的法向量,
l
向量法证明线线平行
向量法证明线线平行
【例2】棱长为2的平行六面体ABCD-A1B1C1D1中,
(1)若点E,F分别是AB,D1C1的中点,求证:CF∥A1E.(基底法)
x
y
z
基底法
坐标法
【例】棱长为2的正方体ABCD-A1B1C1D1中,
(2)若点M,N分别是BC1,CC1的中点,求证:MN∥平面A1BD.
向量法证明线面平行
x
y
z
向量法证明面面平行
【例】棱长为2的正方体ABCD-A1B1C1D1中,
(3)若点G,K分别是DD1,CC1的中点,O为底面ABCD的中心,
求证:平面GHA∥平面D1BK.
x
y
z
x
y
z
P30-例3.长方体ABCD-A1B1C1D1中,AB=4,BC=3,CC1=2,
线段B1C上是否存在点P,使得A1P∥平面ACD1.
平行中的动点问题
总结:直线、平行的平行问题
1.证线线平行:
①证平行四边形得对边平行;
②中位线;
③对应线段成比例;
④平行线的传递性;
⑤线面平行的定义
⑥两直线的方向向量共线(直接法/基底法/坐标法找λ)
2.证线面平行:
①线面平行的判定定理:几何法、基底法、坐标法
平面外的直线l与平面α内的一条直线平行,则l//α.
②法向量坐标法:直线的方向向量与平面的法向量垂直
③直线的方向向量与平面内两个不共线的向量共面.
3.证面面平行:
①面面平行的判定定理:几何法、基底法、坐标法
平面α内的两条相交直线均平行于平面β,则α//β.
②法向量坐标法:两平面的法向量共线
03
空间中直线和平面的垂直
设,是l1,l2,l的方向向量,是平面α,β的法向量,
空间中直线、平面垂直的向量表示
l1
l2
l
P20-例2. 如图所示,在正方体ABCD –A1B1C1D1中,E, F分别是BB1, D1B1的中点,求证:EF⊥DA1.
A
D
C
B
A1
D1
C1
B1
E
F
点的坐标
向量的坐标
向量的
坐标运算
几何
关系
翻译
建系
x
y
z
例题;棱长为2的正方体ABCD-A1B1C1D1中,E,F,M分别为棱AB,BC,B1B的中点,求证:D1M⊥平面B1EF.
向量法证线线垂直
