物理人教版(2019)选择性必修第二册1.3带电粒子在匀强磁场中的运动(共54张ppt)
文档属性
| 名称 | 物理人教版(2019)选择性必修第二册1.3带电粒子在匀强磁场中的运动(共54张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-09-04 20:22:57 | ||
图片预览











文档简介
(共54张PPT)
提出问题
沿着与磁场垂直的方向射入磁场的带电粒子,在匀强磁场中做什么运动?
V
-
F洛
V
-
F洛
V
-
F洛
V
-
F洛
第3节
带电粒子在匀强磁场中的运动
一、带电粒子在匀强磁场中的运动
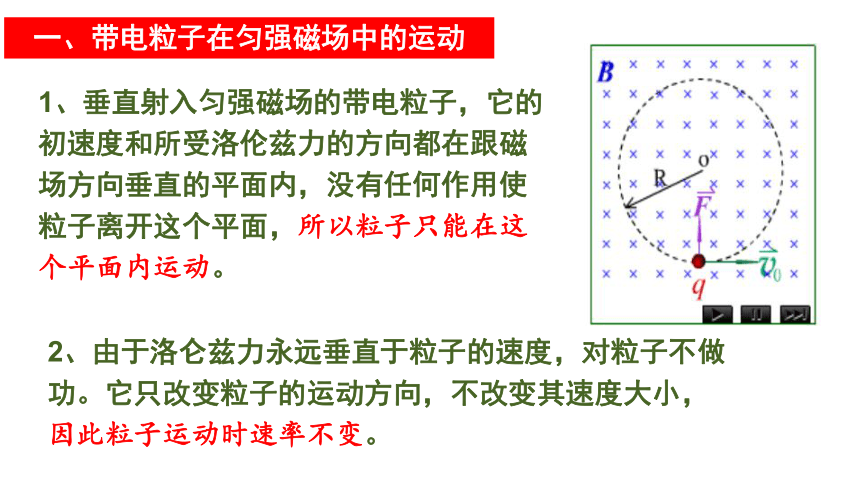
1、垂直射入匀强磁场的带电粒子,它的初速度和所受洛伦兹力的方向都在跟磁场方向垂直的平面内,没有任何作用使粒子离开这个平面,所以粒子只能在这个平面内运动。
2、由于洛仑兹力永远垂直于粒子的速度,对粒子不做功。它只改变粒子的运动方向,不改变其速度大小,因此粒子运动时速率不变。
一、带电粒子在匀强磁场中的运动
3、由于粒子速度大小不变,所以粒子在匀强磁场中所受洛仑兹力的大小也不改变,加之洛仑兹力总是与速度方向垂直,正好起到了向心力的作用。所以沿着与磁场垂直的方向射入磁场的带电粒子,在匀强磁场中做匀速圆周运动。
实验验证
电子枪
玻璃泡
励磁线圈
无磁场
实验验证
有磁场
实验现象:在暗室中可以清楚地看到,在没有磁场作用时,电子的轨迹是直线;在管外加上垂直初速度方向的匀强磁场,电子的轨迹变弯曲成圆形。
例1、下列各图反映带电粒子在匀强磁场中沿垂直于磁场的方向做匀速圆周运动。其中正确的是()
+q
v
F
+q
v
F
-q
v
F
+q
v
F
A B C D
CD
一、带电粒子在匀强磁场中的运动
沿着与磁场垂直的方向射入磁场的带电粒子,在匀强磁场中做匀速圆周运动。
1、轨道半径
带电粒子只受洛伦兹力,作圆周运动,洛伦兹力提供向心力:
解得:
一、带电粒子在匀强磁场中的运动
沿着与磁场垂直的方向射入磁场的带电粒子,在匀强磁场中做匀速圆周运动。
1、轨道半径
2、运行周期
(周期跟轨道半径和运动速率均无关)
②
①
1.两个相同的粒子,速度大小不同,轨迹如图所示。试分析两轨迹对应粒子速度的大小关系
2.比较它们的周期大小
例2、如图所示,在垂直纸面向里的匀强磁场中,有a、b两个电子从同一处沿垂直磁感线方向开始运动,a的初速度为v,b的初速度为2v.则()
A.a先回到出发点
B.b先回到出发点
C.a、b的轨迹是一
对内切圆,且b的半径大
D.a、b的轨迹是一
对外切圆,且b的半径大
a
b
例3、一带电粒子在磁感强度为B的匀强磁场中做匀速圆周运动,如它又顺利进入另一磁感强度为2B的匀强磁场中仍做匀速圆周运动,则( )
A.粒子的速率加倍,周期减半
B.粒子的速率不变,轨道半径减半
C.粒子的速率减半,轨道半径变为原来的 1/4
D.粒子速率不变,周期减半
例4、一个带电粒子沿垂直于磁场的方向射入一个匀强磁场,粒子后段轨迹如图所示,轨迹上的每一小段都可近似看成是圆弧.由于带电粒子使沿途的空气电离,粒子的能量逐渐减少(带电量不变).从图中情况可以确定( )
A.粒子从a到b,带正电
B.粒子从b到a,带正电
C.粒子从a到b,带负电
D.粒子从b到a,带负电
带电粒子在气泡室运动径迹的照片
(1)不同带电粒子的径迹半径为何不同?
(2)同一径迹上为什么曲率半径越来越小?
气泡室是由一密闭容器组成,容器中盛有工作液体,当其处于过热状态时,带电粒子所经轨迹上不断与液体原子发生碰撞 ,而以这些离子为核心形成气泡 。
气泡室
例5.氘核和α粒子,从静止开始经相同电场加速后,垂直进入同一匀强磁场作圆周运动.则这两个粒子的
(1)动能之比为多少
(2)轨道半径之比为多少
(3)周期之比为多少
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
照相底片
质谱仪的示意图
二、质谱仪
利用电场加速
利用磁场偏转
质谱仪是一种分析同位素、测定带电粒子比荷及测定带电粒子质量的重要工具。
例.一个质量为m、电荷量为q的粒子,从容器下方的小孔S1飘入电势差为U的加速电场,其初速度几乎为零,然后经过S3沿着与磁场垂直的方向进入磁感应强度为B的匀强磁场中,最后打到照相底片D上.
二、质谱仪
(1)求粒子进入磁场时的速率
(2)求粒子在磁场中运动的轨道半径
偏
转
:
质谱仪最初是由汤姆生的学生阿斯顿设计的,他用质谱仪发现了氖20和氖22,证实了同位素的存在。现在质谱仪已经是一种十分精密的仪器,是测量带电粒子的质量和分析同位素的重要工具。
例5、如图所示,一质量为m,电荷量为q的粒子从容器A下方小孔S1飘入电势差为U=800V的加速电场,然后经过S3沿着与磁场垂直的方向进入磁感应强度为B=0.40T的匀强磁场中,最后打到底片D上.测得粒子在磁场中运动的轨道半径为r=5cm。求带电粒子的比荷是多少?
要认识原子核内部的情况,必须把核“打开”进行“观察”。然而,原子核被强大的核力约束,只有用极高能量的粒子作为“炮弹”去轰击,才能把它“打开”。产生这些高能“炮弹”的“工厂”就是各种各样的粒子加速器。
粒子加速器
三、回旋加速器
1.加速原理:利用加速电场对带电粒子做正功使带电粒子的动能增加,qU= Ek.
2.直线加速器,多级加速
如图所示是多级加速装置的原理图:
(一)直线加速器
3.困难:技术上不能产生过高电压;加速设备长。
三、回旋加速器
(一)直线加速器
(二)回旋加速器
解决上述困难的一个途径是把加速电场“卷起来”,用磁场控制轨迹,用电场进行加速。
三、回旋加速器
原理:电场使粒子加速,磁场使粒子回旋。
回旋周期: ,与半径、速度的大小无关。
离盒时粒子的最大动能:
与加速电压无关,由半径决定。
此加速器可将质子和氘核加速到1MeV的能量,为此1939年劳伦斯获得诺贝尔物理学奖.
1932年劳伦斯研制第一台回旋加速器的D型室.
三、回旋加速器
C
D
B
v
α
(1)若电子后来又经过D点,则电子的速度大小是多少?
(2)电子从C到D经历的时间是多少?
(电子质量me=9.1x10-31kg,电量e=1.6x10-19C)
8.0x106m/s 6.5x10-9s
例1、如图,在B=9.1x10-4T的匀强磁场中,C、D是垂直于磁场方向的同一平面上的两点,相距d=0.05m。在磁场中运动的电子经过C点时的速度方向与CD成α=300角,并与CD在同一平面内,问:
1.带电粒子在无界磁场中的运动
例2.如图,虚线上方存在磁感应强度为B的磁场,一带正电的粒子质量m、电量q,若它以速度v沿与虚线成300、900、1500、1800角分别射入,
1.请作出上述几种情况下粒子的轨迹
2.观察入射速度、出射速度与虚线夹角间的关系
3.求其在磁场中运动的时间。
2.带电粒子在半无界磁场中的运动
入射角300时
入射角900时
入射角1500时
入射角1800时
例3:如图所示,在y<0的区域内存在匀强磁场,磁场方向如图,磁感应强度为B。一带正电的粒子以速度v从O点射入磁场,入射方向在xoy平面内,与x轴正向的夹角为θ。若粒子射出磁场的位置与O点的距离为L,求该粒子的比荷q/m。
x
y
o
p
θ
v
θ
θ
v
θ
入射速度与边界夹角=出射速度与边界夹角
y
解析:
设粒子进入磁场做圆周运动的半径为R,
在RtΔPOA中,PO=L, PA=2R,则
x
O
P
θ
v
θ
θ
v
θ
θ
A
d
B
e
θ
v
例3如图所示,一束电子(电荷量为e)以速度v垂直射入磁感应强度为B、宽度为d的匀强磁场,穿出磁场时的速度方向与原来入射方向的夹角θ=30°。求 : (1) 电子的质量m= (2) 电子在磁场中的运动时间t=
3、穿过双边界磁场区。
30°
1.圆心在哪里
2.轨迹半径是多少
O
B
d
v
r=d/sin 30o =2d
r=mv/qB
t=( 30o /360o)T= T/12
T=2πm/qB
T=2πr/v
小结:
r
t/T= 30o /360o
A
=30°
v
qvB=mv2/r
t=T/12=πm/6qB
3、偏转角=圆心角
1、两洛伦兹力的交点即圆心
2、偏转角:初末速度的夹角。
4.穿透磁场的时间如何求?
3、圆心角θ =
θ
t=T/12= πd/3v
m=qBr/v=2qdB/v
F
F
d
B
e
θ
v
例3如图所示,一束电子(电荷量为e)以速度v垂直射入磁感应强度为B、宽度为d的匀强磁场,穿出磁场时的速度方向与原来入射方向的夹角θ=30°。求 : (1) 电子的质量m= (2) 电子在磁场中的运动时间t=
O
θ
r
s
3、穿过双边界磁场区。
y
x
O
v
v
a
B
60
例4、 一个质量为m电荷量为q的带电粒子(不计重力)从x轴上的P(a,0)点以速度v,沿与x正方向成60 的方向射入第一象限内的匀强磁场中,并恰好垂直于y轴射出第一象限。求匀强磁场的磁感应强度B和射出点的坐标。
Bq
mv
a
r
3
2
=
=
aq
mv
B
2
3
=
得
射出点坐标为(0, )
a
3
O′
解析 :
例5、如图所示,虚线所围区域内有方向垂直纸面向里的匀强磁场,磁感应强度为B。一束电子沿圆形区域的直径方向以速度v射入磁场,电子束经过磁场区后,其运动的方向与原入射方向成θ角。设电子质量为m,电荷量为e,不计电子之间的相互作用力及所受的重力。求:
(1)电子在磁场中运动轨迹的半径R;
(2)电子在磁场中运动的时间t;
(3)圆形磁场区域的半径r。
B
O
v
v
θ
r
B
v
q
m
L
L
v
O
r1
例6、长为L的水平极板间,有垂直纸面向内的匀强磁场,如图所示,磁场强度为B,板间距离也为L,板不带电,现有质量为m,电量为q的带负电粒子(不计重力),从左边极板间中点处垂直磁场以速度v平行极板射入磁场,欲使粒子不打在极板上,则粒子入射速度v应满足什么条件?
解决带电粒子在匀强磁场中运动的基本环节
找圆心:
已知两个速度方向:可找到两条半径,其交点是圆心。
已知入射方向和出射点的位置:通过入射点作入射方向的垂线,连接入射点和出射点,作中垂线,交点是圆心。
v
v
O
v
O
定半径:
几何法求半径
公式求半径
算时间:
qB
T
t =
q m
p
q
=
2
θ
θ
α
α
α
θ = 2α
注意:θ 应以弧度表示
当带电粒子从同一边界入射出射时速度与边界夹角相同
——对称性
常见的几种情形
带电粒子在匀强磁场中的运动
—— 动态分析问题
例、如图,若电子的电量e,质量m,磁感应强度B及宽度d已知,若要求电子不从右边界穿出,则初速度v0应满足什么条件?
d
e
B
v0
d
e
B
v0
r+rcos60 = d
d
e
B
v0
变化1:若v0向上与边界成60 角,则v0应满足什么条件?
变化2:若v0向下与边界成60 角,则v0应满足什么条件?
r-rcos60 = d
A
Q
B
P
v
B
代入数据得:
3
= (2- )d
QM = rm-
rm2-d 2
PH = 2d,
QN = d,
例、如图,A、B为水平放置的足够长的平行板,板间距离为 d =1.0×10-2m,A板上有一电子源P,Q点在P点正上方B板上,在纸面内从P点向Q点发射速度在0~3.2×107m/s范围内的电子。若垂直纸面内加一匀强磁场,磁感应强度B=9.1×10-3T,已知电子质量 m=9.1×10-31kg ,电子电量 q=1.6×10-19C ,不计电子重力和电子间的相互作用力,且电子打到板上均被吸收,并转移到大地,求电子击在A、B两板上的范围。
解析 :
rm
rm
M
N
H
电子打在A板上的范围是PH段。
电子打在B板上的范围是MN段。
因 qvB=mv2/rm
得: rm=2d
q
a
O
d
b
c
B
v0
R1
例、如图,一端无限伸长的矩形区域abcd内存在着磁感应强度大小为B,方向垂直纸面向里的匀强磁场。从边ad中点O射入一速率v0、方向与Od夹角θ=30 的正电粒子,粒子质量为m,重力不计,带电量为q,已知ad=L。
(1)要使粒子能从ab边射出磁场,求v0的取值范围。
(2)取不同v0值,求粒子在磁场中运动时间t 的范围? (3)从ab边射出的粒子在磁场中运动时间t 的范围。
R1+R1sin30 = L/2
解:(1)
得R1 = L/3
R2
R2- R2cos60 = L/2
得:R2 = L。
(1) ≥v0≥
例、如图,一端无限伸长的矩形区域abcd内存在着磁感应强度大小为B,方向垂直纸面向里的匀强磁场。从边ad中点O射入一速率v0、方向与Od夹角θ=30 的正电粒子,粒子质量为m,重力不计,带电量为q,已知ad=L。
(1)要使粒子能从ab边射出磁场,求v0的取值范围。
(2)取不同v0值,求粒子在磁场中运动时间t 的范围? (3)从ab边射出的粒子在磁场中运动时间t 的范围。
解:(2)
q
a
O
d
b
c
B
v0
R1
R2
解:(3)
≤ t ≤
5 m
6Bq
4 m
3Bq
≤ t ≤
m
3Bq
5 m
3Bq
2R
R
2R
M
N
O
2R
R
2R
M
N
O
2R
2R
2R
M
N
O
R
2R
2R
M
N
O
D.
A.
B.
C.
M
N
B
O
A
例、如图,水平放置的平板MN上方有方向垂直于纸面向里的匀强磁场,磁感应强度为B,许多质量为m,带电量为+q的粒子,以相同的速率 v 沿位于纸面内的各个方向,由小孔O射入磁场区域,不计重力,不计粒子间的相互影响。下列图中阴影部分表示带电粒子可能经过的区域,其中R=mv/qB,哪个图是正确的?( )
……以速率 v 沿纸面各个方向由小孔O射入磁场
2R
R
2R
O
2R
R
2R
O
2R
2R
2R
O
R
2R
2R
O
D.
A.
B.
C.
如图,真空室内存在方向垂直纸面向里,大小B=0.6T的
匀强磁场,内有与磁场方向平行的板ab,在距ab距离为
l=16cm处,有一点状的放射源S向各个方向发射α粒子,
α粒子的速度都是v=3.0×106 m/s,已知α粒子的电荷与
质量之比q/m= 5.0×107 C/kg ,现只考虑在图纸平面中运
动的α粒子,求ab上被α粒子打中的区域的长度。
b
a
S
l
B
即:2R > l > R。
P1
N
P2
故P1P2=20cm
解析:α 粒子带正电,沿逆时针方向做匀速圆周运动,轨道半径R为
例、如图,半径为 r=3×10-2m的圆形区域内有一匀强磁场B=0.2T,一带正电粒子以速度v0=106m/s的从a点处射入磁场,该粒子荷质比为q/m=108C/kg,不计重力。若要使粒子飞离磁场时有最大的偏转角,其入射时粒子的方向应如何(以v0与ao的夹角表示)?最大偏转角多大?
O
a
B
v0
b
α
α
R
r
说明:1.本题中,由于是两圆相交,两个交点的连线同时是两个圆的弦。2.轨道圆半径确定时,弦线越长,通过的弧越长,偏转角度也越大。
R =mv/Bq=5×10-2m > r
解析:
O
a
B
v0
b
α
α
R
r
得 = 37 ,
sin = r/R
最大偏转角为 2 = 74 。
提出问题
沿着与磁场垂直的方向射入磁场的带电粒子,在匀强磁场中做什么运动?
V
-
F洛
V
-
F洛
V
-
F洛
V
-
F洛
第3节
带电粒子在匀强磁场中的运动
一、带电粒子在匀强磁场中的运动
1、垂直射入匀强磁场的带电粒子,它的初速度和所受洛伦兹力的方向都在跟磁场方向垂直的平面内,没有任何作用使粒子离开这个平面,所以粒子只能在这个平面内运动。
2、由于洛仑兹力永远垂直于粒子的速度,对粒子不做功。它只改变粒子的运动方向,不改变其速度大小,因此粒子运动时速率不变。
一、带电粒子在匀强磁场中的运动
3、由于粒子速度大小不变,所以粒子在匀强磁场中所受洛仑兹力的大小也不改变,加之洛仑兹力总是与速度方向垂直,正好起到了向心力的作用。所以沿着与磁场垂直的方向射入磁场的带电粒子,在匀强磁场中做匀速圆周运动。
实验验证
电子枪
玻璃泡
励磁线圈
无磁场
实验验证
有磁场
实验现象:在暗室中可以清楚地看到,在没有磁场作用时,电子的轨迹是直线;在管外加上垂直初速度方向的匀强磁场,电子的轨迹变弯曲成圆形。
例1、下列各图反映带电粒子在匀强磁场中沿垂直于磁场的方向做匀速圆周运动。其中正确的是()
+q
v
F
+q
v
F
-q
v
F
+q
v
F
A B C D
CD
一、带电粒子在匀强磁场中的运动
沿着与磁场垂直的方向射入磁场的带电粒子,在匀强磁场中做匀速圆周运动。
1、轨道半径
带电粒子只受洛伦兹力,作圆周运动,洛伦兹力提供向心力:
解得:
一、带电粒子在匀强磁场中的运动
沿着与磁场垂直的方向射入磁场的带电粒子,在匀强磁场中做匀速圆周运动。
1、轨道半径
2、运行周期
(周期跟轨道半径和运动速率均无关)
②
①
1.两个相同的粒子,速度大小不同,轨迹如图所示。试分析两轨迹对应粒子速度的大小关系
2.比较它们的周期大小
例2、如图所示,在垂直纸面向里的匀强磁场中,有a、b两个电子从同一处沿垂直磁感线方向开始运动,a的初速度为v,b的初速度为2v.则()
A.a先回到出发点
B.b先回到出发点
C.a、b的轨迹是一
对内切圆,且b的半径大
D.a、b的轨迹是一
对外切圆,且b的半径大
a
b
例3、一带电粒子在磁感强度为B的匀强磁场中做匀速圆周运动,如它又顺利进入另一磁感强度为2B的匀强磁场中仍做匀速圆周运动,则( )
A.粒子的速率加倍,周期减半
B.粒子的速率不变,轨道半径减半
C.粒子的速率减半,轨道半径变为原来的 1/4
D.粒子速率不变,周期减半
例4、一个带电粒子沿垂直于磁场的方向射入一个匀强磁场,粒子后段轨迹如图所示,轨迹上的每一小段都可近似看成是圆弧.由于带电粒子使沿途的空气电离,粒子的能量逐渐减少(带电量不变).从图中情况可以确定( )
A.粒子从a到b,带正电
B.粒子从b到a,带正电
C.粒子从a到b,带负电
D.粒子从b到a,带负电
带电粒子在气泡室运动径迹的照片
(1)不同带电粒子的径迹半径为何不同?
(2)同一径迹上为什么曲率半径越来越小?
气泡室是由一密闭容器组成,容器中盛有工作液体,当其处于过热状态时,带电粒子所经轨迹上不断与液体原子发生碰撞 ,而以这些离子为核心形成气泡 。
气泡室
例5.氘核和α粒子,从静止开始经相同电场加速后,垂直进入同一匀强磁场作圆周运动.则这两个粒子的
(1)动能之比为多少
(2)轨道半径之比为多少
(3)周期之比为多少
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
照相底片
质谱仪的示意图
二、质谱仪
利用电场加速
利用磁场偏转
质谱仪是一种分析同位素、测定带电粒子比荷及测定带电粒子质量的重要工具。
例.一个质量为m、电荷量为q的粒子,从容器下方的小孔S1飘入电势差为U的加速电场,其初速度几乎为零,然后经过S3沿着与磁场垂直的方向进入磁感应强度为B的匀强磁场中,最后打到照相底片D上.
二、质谱仪
(1)求粒子进入磁场时的速率
(2)求粒子在磁场中运动的轨道半径
偏
转
:
质谱仪最初是由汤姆生的学生阿斯顿设计的,他用质谱仪发现了氖20和氖22,证实了同位素的存在。现在质谱仪已经是一种十分精密的仪器,是测量带电粒子的质量和分析同位素的重要工具。
例5、如图所示,一质量为m,电荷量为q的粒子从容器A下方小孔S1飘入电势差为U=800V的加速电场,然后经过S3沿着与磁场垂直的方向进入磁感应强度为B=0.40T的匀强磁场中,最后打到底片D上.测得粒子在磁场中运动的轨道半径为r=5cm。求带电粒子的比荷是多少?
要认识原子核内部的情况,必须把核“打开”进行“观察”。然而,原子核被强大的核力约束,只有用极高能量的粒子作为“炮弹”去轰击,才能把它“打开”。产生这些高能“炮弹”的“工厂”就是各种各样的粒子加速器。
粒子加速器
三、回旋加速器
1.加速原理:利用加速电场对带电粒子做正功使带电粒子的动能增加,qU= Ek.
2.直线加速器,多级加速
如图所示是多级加速装置的原理图:
(一)直线加速器
3.困难:技术上不能产生过高电压;加速设备长。
三、回旋加速器
(一)直线加速器
(二)回旋加速器
解决上述困难的一个途径是把加速电场“卷起来”,用磁场控制轨迹,用电场进行加速。
三、回旋加速器
原理:电场使粒子加速,磁场使粒子回旋。
回旋周期: ,与半径、速度的大小无关。
离盒时粒子的最大动能:
与加速电压无关,由半径决定。
此加速器可将质子和氘核加速到1MeV的能量,为此1939年劳伦斯获得诺贝尔物理学奖.
1932年劳伦斯研制第一台回旋加速器的D型室.
三、回旋加速器
C
D
B
v
α
(1)若电子后来又经过D点,则电子的速度大小是多少?
(2)电子从C到D经历的时间是多少?
(电子质量me=9.1x10-31kg,电量e=1.6x10-19C)
8.0x106m/s 6.5x10-9s
例1、如图,在B=9.1x10-4T的匀强磁场中,C、D是垂直于磁场方向的同一平面上的两点,相距d=0.05m。在磁场中运动的电子经过C点时的速度方向与CD成α=300角,并与CD在同一平面内,问:
1.带电粒子在无界磁场中的运动
例2.如图,虚线上方存在磁感应强度为B的磁场,一带正电的粒子质量m、电量q,若它以速度v沿与虚线成300、900、1500、1800角分别射入,
1.请作出上述几种情况下粒子的轨迹
2.观察入射速度、出射速度与虚线夹角间的关系
3.求其在磁场中运动的时间。
2.带电粒子在半无界磁场中的运动
入射角300时
入射角900时
入射角1500时
入射角1800时
例3:如图所示,在y<0的区域内存在匀强磁场,磁场方向如图,磁感应强度为B。一带正电的粒子以速度v从O点射入磁场,入射方向在xoy平面内,与x轴正向的夹角为θ。若粒子射出磁场的位置与O点的距离为L,求该粒子的比荷q/m。
x
y
o
p
θ
v
θ
θ
v
θ
入射速度与边界夹角=出射速度与边界夹角
y
解析:
设粒子进入磁场做圆周运动的半径为R,
在RtΔPOA中,PO=L, PA=2R,则
x
O
P
θ
v
θ
θ
v
θ
θ
A
d
B
e
θ
v
例3如图所示,一束电子(电荷量为e)以速度v垂直射入磁感应强度为B、宽度为d的匀强磁场,穿出磁场时的速度方向与原来入射方向的夹角θ=30°。求 : (1) 电子的质量m= (2) 电子在磁场中的运动时间t=
3、穿过双边界磁场区。
30°
1.圆心在哪里
2.轨迹半径是多少
O
B
d
v
r=d/sin 30o =2d
r=mv/qB
t=( 30o /360o)T= T/12
T=2πm/qB
T=2πr/v
小结:
r
t/T= 30o /360o
A
=30°
v
qvB=mv2/r
t=T/12=πm/6qB
3、偏转角=圆心角
1、两洛伦兹力的交点即圆心
2、偏转角:初末速度的夹角。
4.穿透磁场的时间如何求?
3、圆心角θ =
θ
t=T/12= πd/3v
m=qBr/v=2qdB/v
F
F
d
B
e
θ
v
例3如图所示,一束电子(电荷量为e)以速度v垂直射入磁感应强度为B、宽度为d的匀强磁场,穿出磁场时的速度方向与原来入射方向的夹角θ=30°。求 : (1) 电子的质量m= (2) 电子在磁场中的运动时间t=
O
θ
r
s
3、穿过双边界磁场区。
y
x
O
v
v
a
B
60
例4、 一个质量为m电荷量为q的带电粒子(不计重力)从x轴上的P(a,0)点以速度v,沿与x正方向成60 的方向射入第一象限内的匀强磁场中,并恰好垂直于y轴射出第一象限。求匀强磁场的磁感应强度B和射出点的坐标。
Bq
mv
a
r
3
2
=
=
aq
mv
B
2
3
=
得
射出点坐标为(0, )
a
3
O′
解析 :
例5、如图所示,虚线所围区域内有方向垂直纸面向里的匀强磁场,磁感应强度为B。一束电子沿圆形区域的直径方向以速度v射入磁场,电子束经过磁场区后,其运动的方向与原入射方向成θ角。设电子质量为m,电荷量为e,不计电子之间的相互作用力及所受的重力。求:
(1)电子在磁场中运动轨迹的半径R;
(2)电子在磁场中运动的时间t;
(3)圆形磁场区域的半径r。
B
O
v
v
θ
r
B
v
q
m
L
L
v
O
r1
例6、长为L的水平极板间,有垂直纸面向内的匀强磁场,如图所示,磁场强度为B,板间距离也为L,板不带电,现有质量为m,电量为q的带负电粒子(不计重力),从左边极板间中点处垂直磁场以速度v平行极板射入磁场,欲使粒子不打在极板上,则粒子入射速度v应满足什么条件?
解决带电粒子在匀强磁场中运动的基本环节
找圆心:
已知两个速度方向:可找到两条半径,其交点是圆心。
已知入射方向和出射点的位置:通过入射点作入射方向的垂线,连接入射点和出射点,作中垂线,交点是圆心。
v
v
O
v
O
定半径:
几何法求半径
公式求半径
算时间:
qB
T
t =
q m
p
q
=
2
θ
θ
α
α
α
θ = 2α
注意:θ 应以弧度表示
当带电粒子从同一边界入射出射时速度与边界夹角相同
——对称性
常见的几种情形
带电粒子在匀强磁场中的运动
—— 动态分析问题
例、如图,若电子的电量e,质量m,磁感应强度B及宽度d已知,若要求电子不从右边界穿出,则初速度v0应满足什么条件?
d
e
B
v0
d
e
B
v0
r+rcos60 = d
d
e
B
v0
变化1:若v0向上与边界成60 角,则v0应满足什么条件?
变化2:若v0向下与边界成60 角,则v0应满足什么条件?
r-rcos60 = d
A
Q
B
P
v
B
代入数据得:
3
= (2- )d
QM = rm-
rm2-d 2
PH = 2d,
QN = d,
例、如图,A、B为水平放置的足够长的平行板,板间距离为 d =1.0×10-2m,A板上有一电子源P,Q点在P点正上方B板上,在纸面内从P点向Q点发射速度在0~3.2×107m/s范围内的电子。若垂直纸面内加一匀强磁场,磁感应强度B=9.1×10-3T,已知电子质量 m=9.1×10-31kg ,电子电量 q=1.6×10-19C ,不计电子重力和电子间的相互作用力,且电子打到板上均被吸收,并转移到大地,求电子击在A、B两板上的范围。
解析 :
rm
rm
M
N
H
电子打在A板上的范围是PH段。
电子打在B板上的范围是MN段。
因 qvB=mv2/rm
得: rm=2d
q
a
O
d
b
c
B
v0
R1
例、如图,一端无限伸长的矩形区域abcd内存在着磁感应强度大小为B,方向垂直纸面向里的匀强磁场。从边ad中点O射入一速率v0、方向与Od夹角θ=30 的正电粒子,粒子质量为m,重力不计,带电量为q,已知ad=L。
(1)要使粒子能从ab边射出磁场,求v0的取值范围。
(2)取不同v0值,求粒子在磁场中运动时间t 的范围? (3)从ab边射出的粒子在磁场中运动时间t 的范围。
R1+R1sin30 = L/2
解:(1)
得R1 = L/3
R2
R2- R2cos60 = L/2
得:R2 = L。
(1) ≥v0≥
例、如图,一端无限伸长的矩形区域abcd内存在着磁感应强度大小为B,方向垂直纸面向里的匀强磁场。从边ad中点O射入一速率v0、方向与Od夹角θ=30 的正电粒子,粒子质量为m,重力不计,带电量为q,已知ad=L。
(1)要使粒子能从ab边射出磁场,求v0的取值范围。
(2)取不同v0值,求粒子在磁场中运动时间t 的范围? (3)从ab边射出的粒子在磁场中运动时间t 的范围。
解:(2)
q
a
O
d
b
c
B
v0
R1
R2
解:(3)
≤ t ≤
5 m
6Bq
4 m
3Bq
≤ t ≤
m
3Bq
5 m
3Bq
2R
R
2R
M
N
O
2R
R
2R
M
N
O
2R
2R
2R
M
N
O
R
2R
2R
M
N
O
D.
A.
B.
C.
M
N
B
O
A
例、如图,水平放置的平板MN上方有方向垂直于纸面向里的匀强磁场,磁感应强度为B,许多质量为m,带电量为+q的粒子,以相同的速率 v 沿位于纸面内的各个方向,由小孔O射入磁场区域,不计重力,不计粒子间的相互影响。下列图中阴影部分表示带电粒子可能经过的区域,其中R=mv/qB,哪个图是正确的?( )
……以速率 v 沿纸面各个方向由小孔O射入磁场
2R
R
2R
O
2R
R
2R
O
2R
2R
2R
O
R
2R
2R
O
D.
A.
B.
C.
如图,真空室内存在方向垂直纸面向里,大小B=0.6T的
匀强磁场,内有与磁场方向平行的板ab,在距ab距离为
l=16cm处,有一点状的放射源S向各个方向发射α粒子,
α粒子的速度都是v=3.0×106 m/s,已知α粒子的电荷与
质量之比q/m= 5.0×107 C/kg ,现只考虑在图纸平面中运
动的α粒子,求ab上被α粒子打中的区域的长度。
b
a
S
l
B
即:2R > l > R。
P1
N
P2
故P1P2=20cm
解析:α 粒子带正电,沿逆时针方向做匀速圆周运动,轨道半径R为
例、如图,半径为 r=3×10-2m的圆形区域内有一匀强磁场B=0.2T,一带正电粒子以速度v0=106m/s的从a点处射入磁场,该粒子荷质比为q/m=108C/kg,不计重力。若要使粒子飞离磁场时有最大的偏转角,其入射时粒子的方向应如何(以v0与ao的夹角表示)?最大偏转角多大?
O
a
B
v0
b
α
α
R
r
说明:1.本题中,由于是两圆相交,两个交点的连线同时是两个圆的弦。2.轨道圆半径确定时,弦线越长,通过的弧越长,偏转角度也越大。
R =mv/Bq=5×10-2m > r
解析:
O
a
B
v0
b
α
α
R
r
得 = 37 ,
sin = r/R
最大偏转角为 2 = 74 。
