福建省莆田2024届高三上学期第一次月考数学试题(含解析)
文档属性
| 名称 | 福建省莆田2024届高三上学期第一次月考数学试题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-05 05:23:49 | ||
图片预览




文档简介
2023—2024学年上学期高三数学第一次月考试卷
(考试时间:120分钟 满分:150分)
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 设集合,则( )
A. B. C. D.
2. 不等式的解集为( )
A. B.
C D.
3. 若,则( )
A. B.
C. D.
4. “”是“”的
A. 充分而不必要条件 B. 必要而不充分条件
C. 充要条件 D. 既不充分也不必要条件
5. 一个圆锥的表面积为,它的侧面展开图是圆心角为的扇形,该圆锥的母线长为
A. B. 4 C. D.
6. 如图是正方体的平面展开图.关于这个正方体,有以下判断:
①平面
②平面
③
④平面平面其中正确判断的序号是.
A. ① ③ B. ② ③ C. ① ② ④ D. ② ③ ④
7. 已知三点都在以为球心的球面上, 两两垂直,三棱锥的体积为,则球的表面积为( )
A. B. C. D.
8. 某公园设置了一些石凳供大家休息,每张石凳是由正方体石料截去八个一样的四面体得到的,如图所示.如果一张石凳的体积是,那么原正方体石料的体积是( )
A. B. C. D.
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9. 在空间中,已知a,b是两条不同的直线,,是两个不同的平面,则下列选项中正确的是( )
A. 若,且,,,则
B. 若,且,,则
C. 若a与b相交,且,,则与相交
D. 若,且,,则
10. 设、为空间中的任意两个非零向量,下列各式中正确的有( )
A B.
C. D.
11. (多选题)如图,在棱长为1的正方体中,P为棱CC1上的动点(点P不与点C,C1重合),过点P作平面分别与棱BC,CD交于M,N两点,若CP=CM=CN,则下列说法正确的是( )
A. A1C⊥平面
B. 存在点P,使得AC1∥平面
C. 存在点P,使得点A1到平面的距离为
D. 用过点P,M,D1的平面去截正方体,得到的截面一定是梯形
12. 设,,则下列结论正确的是( )
A. 不等式恒成立
B. 函数的最小值为2
C. 函数的最大值
D. 若,则的最小值为
三、填空题:本题共4小题,每小题5分,共20分.
13. 已知,,,则的最小值为__________.
14. 三棱锥,则点P到底面的距离为_____________.
15. 有一块多边形的菜地,其水平放置的平面图形用斜二测画法画出的直观图是直角梯形(如图所示),,.,则这块菜地的面积为___________.
16. 在三棱锥中,,,则三棱锥外接球的体积是______.
四、解答题:本题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.
17. 设集合,或.
(1)若,求;
(2)若,求实数的取值范围.
18. 已知关于的不等式的解集为或.
(1)求a,b的值;
(2)求关于的不等式的解集.
19. (1)已知命题,使得是真命题,求实数的取值范围;
(2)已知,,若是必要不充分条件,求实数的取值范围.
20. 某公司一年购买某种货物600吨,每次购买吨(且x是600的约数),运费为6万元/次,一年的总存储费用为万元.
(1)写出一年的总运费与总存储费用之和(万元)与的函数关系式;
(2)求一年的总运费与总存储费用之和的最小值,并求出此时每次应购买多少吨.
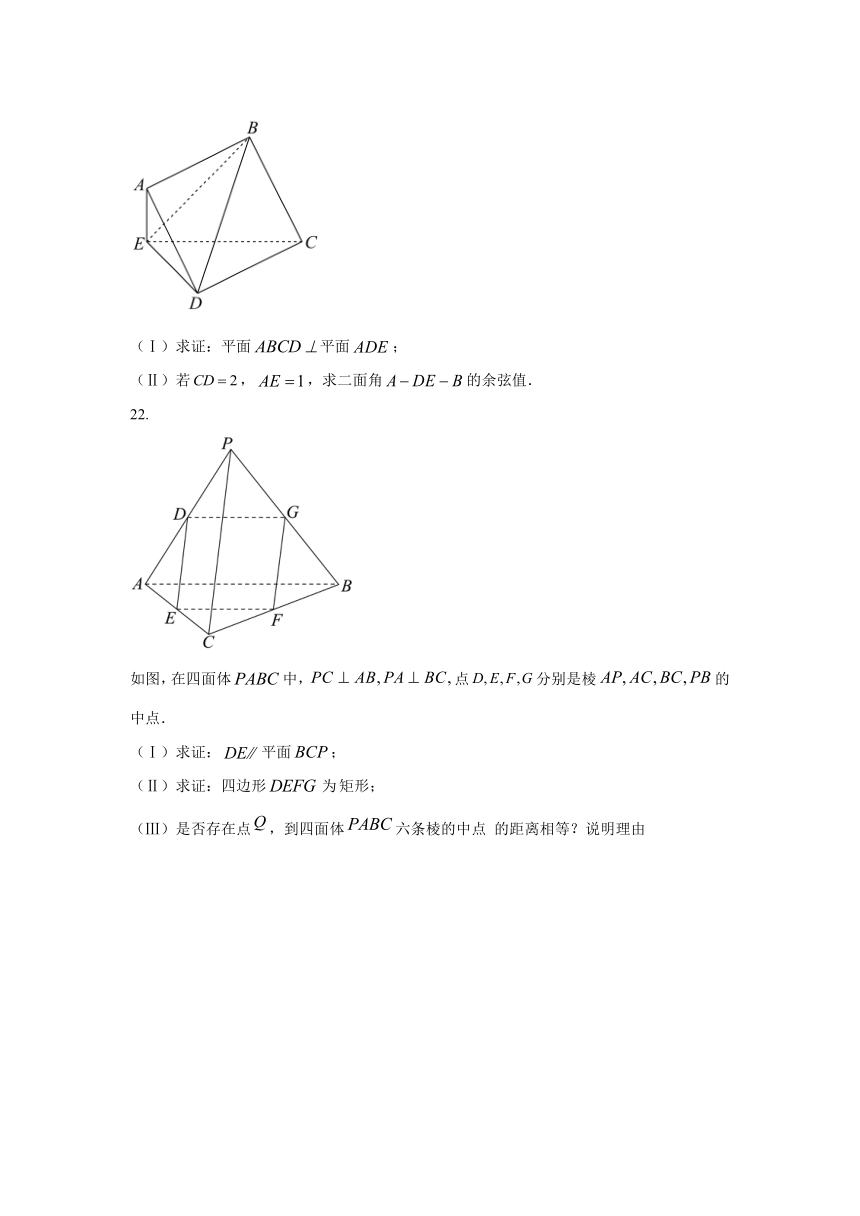
21. 如图,正方形所在平面与所在的平面交于,且平面.
(Ⅰ)求证:平面平面;
(Ⅱ)若,,求二面角的余弦值.
22.
如图,在四面体中,点分别是棱的中点.
(Ⅰ)求证:平面;
(Ⅱ)求证:四边形矩形;
(Ⅲ)是否存在点,到四面体六条棱的中点 的距离相等?说明理由
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 设集合,则( )
A. B. C. D.
【答案】B
【解析】
【分析】解不等式求得集合,从而求得.
【详解】,解得,所以.
,所以,所以,
所以.
故选:B
2. 不等式的解集为( )
A. B.
C D.
【答案】D
【解析】
【分析】根据一元二次不等式的解法进行求解即可.
【详解】或,
故选:D
3. 若,则( )
A. B.
C. D.
【答案】A
【解析】
【分析】由利用指数函数的单调性可判断A;由对数运算可判断B;利用不等式的性质可判断C;举反例可判断D.
【详解】对于A,因为,所以,
可得,所以,故A错误;
对于B,由得,所以,
可得,故B错误;
对于C,因为,所以,,又,
所以,故C正确;
对于D,若,则,故D错误.
故选:C.
4. “”是“”的
A. 充分而不必要条件 B. 必要而不充分条件
C. 充要条件 D. 既不充分也不必要条件
【答案】A
【解析】
【分析】
利用充分条件和必要条件的定义进行判断
【详解】解:当时,,所以 ,
当时,,所以 ,即
所以“”是“”的充分不必要条件
故选:A
【点睛】此题考查充分条件,必要条件的应用,属于基础题
5. 一个圆锥的表面积为,它的侧面展开图是圆心角为的扇形,该圆锥的母线长为
A. B. 4 C. D.
【答案】B
【解析】
【分析】
设圆锥的底面半径为,母线长为,利用扇形面积公式和圆锥表面积公式,求出圆锥的底面圆半径和母线长.
【详解】设圆锥的底面半径为,母线长为
它的侧面展开图是圆心角为的扇形
又圆锥的表面积为 ,解得:
母线长为:
本题正确选项:
【点睛】本题考查了圆锥的结构特征与应用问题,关键是能够熟练应用扇形面积公式和圆锥表面积公式,是基础题.
6. 如图是正方体的平面展开图.关于这个正方体,有以下判断:
①平面
②平面
③
④平面平面其中正确判断的序号是.
A. ① ③ B. ② ③ C. ① ② ④ D. ② ③ ④
【答案】C
【解析】
【分析】还原正方体直观图,根据正方体性质,结合线面垂直判定定理可判断①;结合线面平行判定定理可判断②;结合直观图直接可判断③;利用面面平行判定定理可判断④.
【详解】由已知中正方体的平面展开图,得到正方体的直观图如下图所示:
因为平面EFMN,平面EFMN,所以
又,,平面ACME,平面EMC,
所以平面,
因为平面,所以,同理
又平面,平面,
所以平面,故①正确;
易知,平面,平面,所以平面,故②正确;
由图可知显然不平行,故③不正确;
易知,平面,平面,所以面,同理可得面,又,平面BDE,平面BDE,由面面平行判定定理可知平面平面,故④正确.
故选:C.
7. 已知三点都在以为球心球面上, 两两垂直,三棱锥的体积为,则球的表面积为( )
A. B. C. D.
【答案】B
【解析】
【分析】由三棱锥体积公式求得球半径,再由球面积公式计算.
【详解】设球的半径为,由题意,可得三棱锥体积,,解得,则球的表面积为,
故选:B.
8. 某公园设置了一些石凳供大家休息,每张石凳是由正方体石料截去八个一样的四面体得到的,如图所示.如果一张石凳的体积是,那么原正方体石料的体积是( )
A. B. C. D.
【答案】B
【解析】
【分析】根据正方体、正四棱锥的体积公式,结合已知进行求解即可.
【详解】设正方体的棱长为,则正方体的体积为,
每一个正四面体的体积为:,
由题意可知:,
故选:B
【点睛】关键点睛:利用空间想象能力是解题的关键.
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9. 在空间中,已知a,b是两条不同的直线,,是两个不同的平面,则下列选项中正确的是( )
A. 若,且,,,则
B. 若,且,,则
C. 若a与b相交,且,,则与相交
D. 若,且,,则
【答案】AC
【解析】
【分析】利用空间线线、线面、面面平行和垂直的判定定理和性质定理分析判断即可
【详解】若,且,,即两平面的法向量平行,则成立,故A正确;
若,且,,则a与b互相平行或相交或异面,故B错误;
若a,b相交,且,,即两平面的法向量相交,则,相交成立,故C正确;
若,且,,则与平行或相交,故D错误;
故选:AC.
【点睛】此题考查空间线线、线面、面面平行和垂直的判定定理和性质定理的应用,属于基础题
10. 设、为空间中的任意两个非零向量,下列各式中正确的有( )
A. B.
C. D.
【答案】BD
【解析】
【分析】利用空间数量积的定义、运算性质逐项判断,可得出合适的选项.
【详解】对于A选项,向量不能作除法,A错;
对于B选项,,B对;
对于C选项,,C错;
对于D选项,,D对.
故选:BD.
11. (多选题)如图,在棱长为1的正方体中,P为棱CC1上的动点(点P不与点C,C1重合),过点P作平面分别与棱BC,CD交于M,N两点,若CP=CM=CN,则下列说法正确的是( )
A. A1C⊥平面
B. 存在点P,使得AC1∥平面
C. 存在点P,使得点A1到平面的距离为
D. 用过点P,M,D1的平面去截正方体,得到的截面一定是梯形
【答案】ACD
【解析】
【分析】连接,首先证明平面,然后由⊥平面可判断A,由平面可判断B,由点A1到平面的距离的取值范围为可判断C,过点P,M,D1的平面去截正方体得到的截面是四边形,可判断D.
【详解】
连接
因为,所以=,所以
又平面,平面,所以平面
同理可证,平面
又,、平面,所以平面平面
易证⊥平面,所以⊥平面,A正确
又平面,所以与平面相交,不存在点P,使得∥平面,B不正确.
因为,点到平面的距离为
所以点A1到平面的距离的取值范围为
又,所以存在点P,使得点A1到平面的距离为,C正确.
因为,所以,所以用过点P,M,D1的平面去截正方体得到的截面是四边形
又,且,所以截面为梯形,D正确
故选:ACD
12. 设,,则下列结论正确的是( )
A. 不等式恒成立
B. 函数的最小值为2
C. 函数的最大值
D. 若,则的最小值为
【答案】AC
【解析】
【分析】化简函数表达式,利用基本不等式求各函数的最值,确定正确选项.
【详解】解:因为,,
,当且仅当时取等号,A正确;
因为,则,当且仅当,即时取等号,
但,故B错误;
,当且仅当,即时取等号,C正确;
因为,所以,
则
,
当且仅当中时取等号,D错误.
故选:AC.
三、填空题:本题共4小题,每小题5分,共20分.
13. 已知,,,则的最小值为__________.
【答案】
【解析】
【分析】利用 的代换和基本不等式即得.
【详解】
,
,当且仅当即时取等号
所以.
故答案为:
14. 三棱锥,则点P到底面的距离为_____________.
【答案】
【解析】
【分析】把三棱锥放入球中分析即可
【详解】
如图,因为,所以可以把三棱锥放入一个球中,其中为球心,为外接圆圆心,则到底面ABC的距离即为OP的长.
在中由正弦定理得,所以
所以
故答案为:
15. 有一块多边形的菜地,其水平放置的平面图形用斜二测画法画出的直观图是直角梯形(如图所示),,.,则这块菜地的面积为___________.
【答案】
【解析】
【分析】首先计算直观图梯形的面积,再根据,即可求解菜地的面积.
【详解】如图,,,
,
因为,所以.
故答案为:
16. 在三棱锥中,,,则三棱锥外接球的体积是______.
【答案】
【解析】
【分析】作出图形,取等边的中心,连接,可知三棱锥外接球球心在直线上,设三棱锥外接球的半径为,根据几何关系列出关于的方程,解出的值,进而可求得三棱锥外接球的体积.
【详解】取等边的中心,连接、,如下图所示:
,,所以,三棱锥为正三棱锥,
所以,三棱锥外接球球心在直线,设该球的半径为,
由正弦定理得,所以,,
由勾股定理得,即,解得,
因此,三棱锥外接球的体积为.
故答案为:.
【点睛】本题考查三棱锥外接球体积的计算,要分析出球心的位置,并结合几何关系列等式求解,考查计算能力,属于中等题.
四、解答题:本题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.
17. 设集合,或.
(1)若,求;
(2)若,求实数的取值范围.
【答案】(1)
(2)
【解析】
【分析】(1)代入集合A中,先求,再求;
(2)由,分和两个类型讨论.
【小问1详解】
若,则,
由或,得,
则;
【小问2详解】
因,当时,,解得,符合题意;
当时,有①或② ,
解①得,解②得,
因为,
所以实数的取值范围.
18. 已知关于的不等式的解集为或.
(1)求a,b的值;
(2)求关于的不等式的解集.
【答案】(1);
(2)答案见解析
【解析】
【分析】(1)将不等式的解集转化为方程的两个根,结合韦达定理求出a,b的值;
(2)在(1)的前提下,对不等式变形为,对分类讨论,求解不等式的解集.
【小问1详解】
易知,
由题意得b,3是关于的方程的两个不相等的实数根,
所以,
解得:,
所以.
【小问2详解】
由(1)得,
当时,不等式无解;
当时,解得:;
当时,解得:.
综上,当时,不等式的解集为;
当时,不等式的解集为;
当时,不等式的解集为.
19. (1)已知命题,使得是真命题,求实数的取值范围;
(2)已知,,若是的必要不充分条件,求实数的取值范围.
【答案】(1);(2)
【解析】
【分析】(1)因为对全体实数x,使得是真命题,即可得到,求出的范围;
(2)分别求出命题 中 的范围,再根据是的必要不充分条件,即可得到关于的不等式,求出的范围.
【详解】(1)因为命题,使得是真命题,那么 ,
即 ,那么实数的取值范围为 ;
(2),即 ;
中,,因为 ,解得 ,是的必要不充分条件,
所以 ,故实数的取值范围为.
20. 某公司一年购买某种货物600吨,每次购买吨(且x是600的约数),运费为6万元/次,一年的总存储费用为万元.
(1)写出一年的总运费与总存储费用之和(万元)与的函数关系式;
(2)求一年的总运费与总存储费用之和的最小值,并求出此时每次应购买多少吨.
【答案】(1),且;(2)每次应购买30吨,一年的总运费与总存储费用之和取得最小值为240(万元).
【解析】
【分析】(1)根据总运费和总存储费用求得关于的函数关系式.
(2)结合基本不等式求得的最小值以及此时对应的的值.
【详解】(1)设每次购买吨,则一年需要购买次,
则总运费为万元,
由已知得,一年的总存储费用为万元,
则,,且,
(2)(万元),
当且仅当,即吨时,y取得最小值,
故每次应购买30吨,一年的总运费与总存储费用之和取得最小值,最小值为240(万元).
21. 如图,正方形所在的平面与所在的平面交于,且平面.
(Ⅰ)求证:平面平面;
(Ⅱ)若,,求二面角的余弦值.
【答案】(Ⅰ)证明见解析;(Ⅱ)
【解析】
【分析】(Ⅰ)先根据线面垂直的判定定理证明平面, 再由面面垂直的判定定理,即可证明结果;(Ⅱ)在平面内,过作,由(Ⅰ)知平面,进而证明平面,所以两两垂直.以,,分别为轴,建立空间直角坐标系,然后再利用空间向量即可求出结果.
【详解】解:(Ⅰ)因为平面,平面,所以,
在正方形中,,又因为,
所以平面,
又因为平面,所以平面平面
(Ⅱ)在平面内,过作,
由(Ⅰ)知平面,所以,
所以,又平面,所以两两垂直.
以,,分别为轴,
建立空间直角坐标系如图所示,
因为,所以,又,所以,
所以,,,,
所以平面的法向量为,
设平面的法向量为,
,,
所以由,得,令,则,
所以,
设二面角为,所以.
22.
如图,在四面体中,点分别是棱的中点.
(Ⅰ)求证:平面;
(Ⅱ)求证:四边形为矩形;
(Ⅲ)是否存在点,到四面体六条棱的中点 的距离相等?说明理由.
【答案】略
【解析】
【详解】:证明:(Ⅰ)因为D,E分别为AP,AC的中点,所以DE//PC.又因为DE平面BCP,所以DE//平面BCP.
(Ⅱ)因为D,E,F,G分别为AP,AC,BC,PB的中点,
所以DE//PC//FG,DG//AB//EF.所以四边形DEFG为平行四边形,
又因PC⊥AB,所以DE⊥DG,所以四边形DEFG为矩形.
(Ⅲ)存在点Q满足条件,理由如下:连接DF,EG,设Q为EG的中点
由(Ⅱ)知,DF∩EG=Q,且QD=QE=QF=QG=EG.
分别取PC,AB的中点M,N,连接ME,EN,NG,MG,MN.
与(Ⅱ)同理,可证四边形MENG为矩形,其对角线点为EG的中点Q,
且QM=QN=EG,所以Q为满足条件的点
(考试时间:120分钟 满分:150分)
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 设集合,则( )
A. B. C. D.
2. 不等式的解集为( )
A. B.
C D.
3. 若,则( )
A. B.
C. D.
4. “”是“”的
A. 充分而不必要条件 B. 必要而不充分条件
C. 充要条件 D. 既不充分也不必要条件
5. 一个圆锥的表面积为,它的侧面展开图是圆心角为的扇形,该圆锥的母线长为
A. B. 4 C. D.
6. 如图是正方体的平面展开图.关于这个正方体,有以下判断:
①平面
②平面
③
④平面平面其中正确判断的序号是.
A. ① ③ B. ② ③ C. ① ② ④ D. ② ③ ④
7. 已知三点都在以为球心的球面上, 两两垂直,三棱锥的体积为,则球的表面积为( )
A. B. C. D.
8. 某公园设置了一些石凳供大家休息,每张石凳是由正方体石料截去八个一样的四面体得到的,如图所示.如果一张石凳的体积是,那么原正方体石料的体积是( )
A. B. C. D.
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9. 在空间中,已知a,b是两条不同的直线,,是两个不同的平面,则下列选项中正确的是( )
A. 若,且,,,则
B. 若,且,,则
C. 若a与b相交,且,,则与相交
D. 若,且,,则
10. 设、为空间中的任意两个非零向量,下列各式中正确的有( )
A B.
C. D.
11. (多选题)如图,在棱长为1的正方体中,P为棱CC1上的动点(点P不与点C,C1重合),过点P作平面分别与棱BC,CD交于M,N两点,若CP=CM=CN,则下列说法正确的是( )
A. A1C⊥平面
B. 存在点P,使得AC1∥平面
C. 存在点P,使得点A1到平面的距离为
D. 用过点P,M,D1的平面去截正方体,得到的截面一定是梯形
12. 设,,则下列结论正确的是( )
A. 不等式恒成立
B. 函数的最小值为2
C. 函数的最大值
D. 若,则的最小值为
三、填空题:本题共4小题,每小题5分,共20分.
13. 已知,,,则的最小值为__________.
14. 三棱锥,则点P到底面的距离为_____________.
15. 有一块多边形的菜地,其水平放置的平面图形用斜二测画法画出的直观图是直角梯形(如图所示),,.,则这块菜地的面积为___________.
16. 在三棱锥中,,,则三棱锥外接球的体积是______.
四、解答题:本题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.
17. 设集合,或.
(1)若,求;
(2)若,求实数的取值范围.
18. 已知关于的不等式的解集为或.
(1)求a,b的值;
(2)求关于的不等式的解集.
19. (1)已知命题,使得是真命题,求实数的取值范围;
(2)已知,,若是必要不充分条件,求实数的取值范围.
20. 某公司一年购买某种货物600吨,每次购买吨(且x是600的约数),运费为6万元/次,一年的总存储费用为万元.
(1)写出一年的总运费与总存储费用之和(万元)与的函数关系式;
(2)求一年的总运费与总存储费用之和的最小值,并求出此时每次应购买多少吨.
21. 如图,正方形所在平面与所在的平面交于,且平面.
(Ⅰ)求证:平面平面;
(Ⅱ)若,,求二面角的余弦值.
22.
如图,在四面体中,点分别是棱的中点.
(Ⅰ)求证:平面;
(Ⅱ)求证:四边形矩形;
(Ⅲ)是否存在点,到四面体六条棱的中点 的距离相等?说明理由
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 设集合,则( )
A. B. C. D.
【答案】B
【解析】
【分析】解不等式求得集合,从而求得.
【详解】,解得,所以.
,所以,所以,
所以.
故选:B
2. 不等式的解集为( )
A. B.
C D.
【答案】D
【解析】
【分析】根据一元二次不等式的解法进行求解即可.
【详解】或,
故选:D
3. 若,则( )
A. B.
C. D.
【答案】A
【解析】
【分析】由利用指数函数的单调性可判断A;由对数运算可判断B;利用不等式的性质可判断C;举反例可判断D.
【详解】对于A,因为,所以,
可得,所以,故A错误;
对于B,由得,所以,
可得,故B错误;
对于C,因为,所以,,又,
所以,故C正确;
对于D,若,则,故D错误.
故选:C.
4. “”是“”的
A. 充分而不必要条件 B. 必要而不充分条件
C. 充要条件 D. 既不充分也不必要条件
【答案】A
【解析】
【分析】
利用充分条件和必要条件的定义进行判断
【详解】解:当时,,所以 ,
当时,,所以 ,即
所以“”是“”的充分不必要条件
故选:A
【点睛】此题考查充分条件,必要条件的应用,属于基础题
5. 一个圆锥的表面积为,它的侧面展开图是圆心角为的扇形,该圆锥的母线长为
A. B. 4 C. D.
【答案】B
【解析】
【分析】
设圆锥的底面半径为,母线长为,利用扇形面积公式和圆锥表面积公式,求出圆锥的底面圆半径和母线长.
【详解】设圆锥的底面半径为,母线长为
它的侧面展开图是圆心角为的扇形
又圆锥的表面积为 ,解得:
母线长为:
本题正确选项:
【点睛】本题考查了圆锥的结构特征与应用问题,关键是能够熟练应用扇形面积公式和圆锥表面积公式,是基础题.
6. 如图是正方体的平面展开图.关于这个正方体,有以下判断:
①平面
②平面
③
④平面平面其中正确判断的序号是.
A. ① ③ B. ② ③ C. ① ② ④ D. ② ③ ④
【答案】C
【解析】
【分析】还原正方体直观图,根据正方体性质,结合线面垂直判定定理可判断①;结合线面平行判定定理可判断②;结合直观图直接可判断③;利用面面平行判定定理可判断④.
【详解】由已知中正方体的平面展开图,得到正方体的直观图如下图所示:
因为平面EFMN,平面EFMN,所以
又,,平面ACME,平面EMC,
所以平面,
因为平面,所以,同理
又平面,平面,
所以平面,故①正确;
易知,平面,平面,所以平面,故②正确;
由图可知显然不平行,故③不正确;
易知,平面,平面,所以面,同理可得面,又,平面BDE,平面BDE,由面面平行判定定理可知平面平面,故④正确.
故选:C.
7. 已知三点都在以为球心球面上, 两两垂直,三棱锥的体积为,则球的表面积为( )
A. B. C. D.
【答案】B
【解析】
【分析】由三棱锥体积公式求得球半径,再由球面积公式计算.
【详解】设球的半径为,由题意,可得三棱锥体积,,解得,则球的表面积为,
故选:B.
8. 某公园设置了一些石凳供大家休息,每张石凳是由正方体石料截去八个一样的四面体得到的,如图所示.如果一张石凳的体积是,那么原正方体石料的体积是( )
A. B. C. D.
【答案】B
【解析】
【分析】根据正方体、正四棱锥的体积公式,结合已知进行求解即可.
【详解】设正方体的棱长为,则正方体的体积为,
每一个正四面体的体积为:,
由题意可知:,
故选:B
【点睛】关键点睛:利用空间想象能力是解题的关键.
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9. 在空间中,已知a,b是两条不同的直线,,是两个不同的平面,则下列选项中正确的是( )
A. 若,且,,,则
B. 若,且,,则
C. 若a与b相交,且,,则与相交
D. 若,且,,则
【答案】AC
【解析】
【分析】利用空间线线、线面、面面平行和垂直的判定定理和性质定理分析判断即可
【详解】若,且,,即两平面的法向量平行,则成立,故A正确;
若,且,,则a与b互相平行或相交或异面,故B错误;
若a,b相交,且,,即两平面的法向量相交,则,相交成立,故C正确;
若,且,,则与平行或相交,故D错误;
故选:AC.
【点睛】此题考查空间线线、线面、面面平行和垂直的判定定理和性质定理的应用,属于基础题
10. 设、为空间中的任意两个非零向量,下列各式中正确的有( )
A. B.
C. D.
【答案】BD
【解析】
【分析】利用空间数量积的定义、运算性质逐项判断,可得出合适的选项.
【详解】对于A选项,向量不能作除法,A错;
对于B选项,,B对;
对于C选项,,C错;
对于D选项,,D对.
故选:BD.
11. (多选题)如图,在棱长为1的正方体中,P为棱CC1上的动点(点P不与点C,C1重合),过点P作平面分别与棱BC,CD交于M,N两点,若CP=CM=CN,则下列说法正确的是( )
A. A1C⊥平面
B. 存在点P,使得AC1∥平面
C. 存在点P,使得点A1到平面的距离为
D. 用过点P,M,D1的平面去截正方体,得到的截面一定是梯形
【答案】ACD
【解析】
【分析】连接,首先证明平面,然后由⊥平面可判断A,由平面可判断B,由点A1到平面的距离的取值范围为可判断C,过点P,M,D1的平面去截正方体得到的截面是四边形,可判断D.
【详解】
连接
因为,所以=,所以
又平面,平面,所以平面
同理可证,平面
又,、平面,所以平面平面
易证⊥平面,所以⊥平面,A正确
又平面,所以与平面相交,不存在点P,使得∥平面,B不正确.
因为,点到平面的距离为
所以点A1到平面的距离的取值范围为
又,所以存在点P,使得点A1到平面的距离为,C正确.
因为,所以,所以用过点P,M,D1的平面去截正方体得到的截面是四边形
又,且,所以截面为梯形,D正确
故选:ACD
12. 设,,则下列结论正确的是( )
A. 不等式恒成立
B. 函数的最小值为2
C. 函数的最大值
D. 若,则的最小值为
【答案】AC
【解析】
【分析】化简函数表达式,利用基本不等式求各函数的最值,确定正确选项.
【详解】解:因为,,
,当且仅当时取等号,A正确;
因为,则,当且仅当,即时取等号,
但,故B错误;
,当且仅当,即时取等号,C正确;
因为,所以,
则
,
当且仅当中时取等号,D错误.
故选:AC.
三、填空题:本题共4小题,每小题5分,共20分.
13. 已知,,,则的最小值为__________.
【答案】
【解析】
【分析】利用 的代换和基本不等式即得.
【详解】
,
,当且仅当即时取等号
所以.
故答案为:
14. 三棱锥,则点P到底面的距离为_____________.
【答案】
【解析】
【分析】把三棱锥放入球中分析即可
【详解】
如图,因为,所以可以把三棱锥放入一个球中,其中为球心,为外接圆圆心,则到底面ABC的距离即为OP的长.
在中由正弦定理得,所以
所以
故答案为:
15. 有一块多边形的菜地,其水平放置的平面图形用斜二测画法画出的直观图是直角梯形(如图所示),,.,则这块菜地的面积为___________.
【答案】
【解析】
【分析】首先计算直观图梯形的面积,再根据,即可求解菜地的面积.
【详解】如图,,,
,
因为,所以.
故答案为:
16. 在三棱锥中,,,则三棱锥外接球的体积是______.
【答案】
【解析】
【分析】作出图形,取等边的中心,连接,可知三棱锥外接球球心在直线上,设三棱锥外接球的半径为,根据几何关系列出关于的方程,解出的值,进而可求得三棱锥外接球的体积.
【详解】取等边的中心,连接、,如下图所示:
,,所以,三棱锥为正三棱锥,
所以,三棱锥外接球球心在直线,设该球的半径为,
由正弦定理得,所以,,
由勾股定理得,即,解得,
因此,三棱锥外接球的体积为.
故答案为:.
【点睛】本题考查三棱锥外接球体积的计算,要分析出球心的位置,并结合几何关系列等式求解,考查计算能力,属于中等题.
四、解答题:本题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.
17. 设集合,或.
(1)若,求;
(2)若,求实数的取值范围.
【答案】(1)
(2)
【解析】
【分析】(1)代入集合A中,先求,再求;
(2)由,分和两个类型讨论.
【小问1详解】
若,则,
由或,得,
则;
【小问2详解】
因,当时,,解得,符合题意;
当时,有①或② ,
解①得,解②得,
因为,
所以实数的取值范围.
18. 已知关于的不等式的解集为或.
(1)求a,b的值;
(2)求关于的不等式的解集.
【答案】(1);
(2)答案见解析
【解析】
【分析】(1)将不等式的解集转化为方程的两个根,结合韦达定理求出a,b的值;
(2)在(1)的前提下,对不等式变形为,对分类讨论,求解不等式的解集.
【小问1详解】
易知,
由题意得b,3是关于的方程的两个不相等的实数根,
所以,
解得:,
所以.
【小问2详解】
由(1)得,
当时,不等式无解;
当时,解得:;
当时,解得:.
综上,当时,不等式的解集为;
当时,不等式的解集为;
当时,不等式的解集为.
19. (1)已知命题,使得是真命题,求实数的取值范围;
(2)已知,,若是的必要不充分条件,求实数的取值范围.
【答案】(1);(2)
【解析】
【分析】(1)因为对全体实数x,使得是真命题,即可得到,求出的范围;
(2)分别求出命题 中 的范围,再根据是的必要不充分条件,即可得到关于的不等式,求出的范围.
【详解】(1)因为命题,使得是真命题,那么 ,
即 ,那么实数的取值范围为 ;
(2),即 ;
中,,因为 ,解得 ,是的必要不充分条件,
所以 ,故实数的取值范围为.
20. 某公司一年购买某种货物600吨,每次购买吨(且x是600的约数),运费为6万元/次,一年的总存储费用为万元.
(1)写出一年的总运费与总存储费用之和(万元)与的函数关系式;
(2)求一年的总运费与总存储费用之和的最小值,并求出此时每次应购买多少吨.
【答案】(1),且;(2)每次应购买30吨,一年的总运费与总存储费用之和取得最小值为240(万元).
【解析】
【分析】(1)根据总运费和总存储费用求得关于的函数关系式.
(2)结合基本不等式求得的最小值以及此时对应的的值.
【详解】(1)设每次购买吨,则一年需要购买次,
则总运费为万元,
由已知得,一年的总存储费用为万元,
则,,且,
(2)(万元),
当且仅当,即吨时,y取得最小值,
故每次应购买30吨,一年的总运费与总存储费用之和取得最小值,最小值为240(万元).
21. 如图,正方形所在的平面与所在的平面交于,且平面.
(Ⅰ)求证:平面平面;
(Ⅱ)若,,求二面角的余弦值.
【答案】(Ⅰ)证明见解析;(Ⅱ)
【解析】
【分析】(Ⅰ)先根据线面垂直的判定定理证明平面, 再由面面垂直的判定定理,即可证明结果;(Ⅱ)在平面内,过作,由(Ⅰ)知平面,进而证明平面,所以两两垂直.以,,分别为轴,建立空间直角坐标系,然后再利用空间向量即可求出结果.
【详解】解:(Ⅰ)因为平面,平面,所以,
在正方形中,,又因为,
所以平面,
又因为平面,所以平面平面
(Ⅱ)在平面内,过作,
由(Ⅰ)知平面,所以,
所以,又平面,所以两两垂直.
以,,分别为轴,
建立空间直角坐标系如图所示,
因为,所以,又,所以,
所以,,,,
所以平面的法向量为,
设平面的法向量为,
,,
所以由,得,令,则,
所以,
设二面角为,所以.
22.
如图,在四面体中,点分别是棱的中点.
(Ⅰ)求证:平面;
(Ⅱ)求证:四边形为矩形;
(Ⅲ)是否存在点,到四面体六条棱的中点 的距离相等?说明理由.
【答案】略
【解析】
【详解】:证明:(Ⅰ)因为D,E分别为AP,AC的中点,所以DE//PC.又因为DE平面BCP,所以DE//平面BCP.
(Ⅱ)因为D,E,F,G分别为AP,AC,BC,PB的中点,
所以DE//PC//FG,DG//AB//EF.所以四边形DEFG为平行四边形,
又因PC⊥AB,所以DE⊥DG,所以四边形DEFG为矩形.
(Ⅲ)存在点Q满足条件,理由如下:连接DF,EG,设Q为EG的中点
由(Ⅱ)知,DF∩EG=Q,且QD=QE=QF=QG=EG.
分别取PC,AB的中点M,N,连接ME,EN,NG,MG,MN.
与(Ⅱ)同理,可证四边形MENG为矩形,其对角线点为EG的中点Q,
且QM=QN=EG,所以Q为满足条件的点
同课章节目录
