1.3正方形的性质与判定 同步知识点分类练习题 北师大版九年级数学上册(含解析)
文档属性
| 名称 | 1.3正方形的性质与判定 同步知识点分类练习题 北师大版九年级数学上册(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 265.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-05 17:18:03 | ||
图片预览




文档简介
2023-2024学年北师大版九年级数学上册《1.3正方形的性质与判定》
同步知识点分类练习题(附答案)
一.正方形的性质
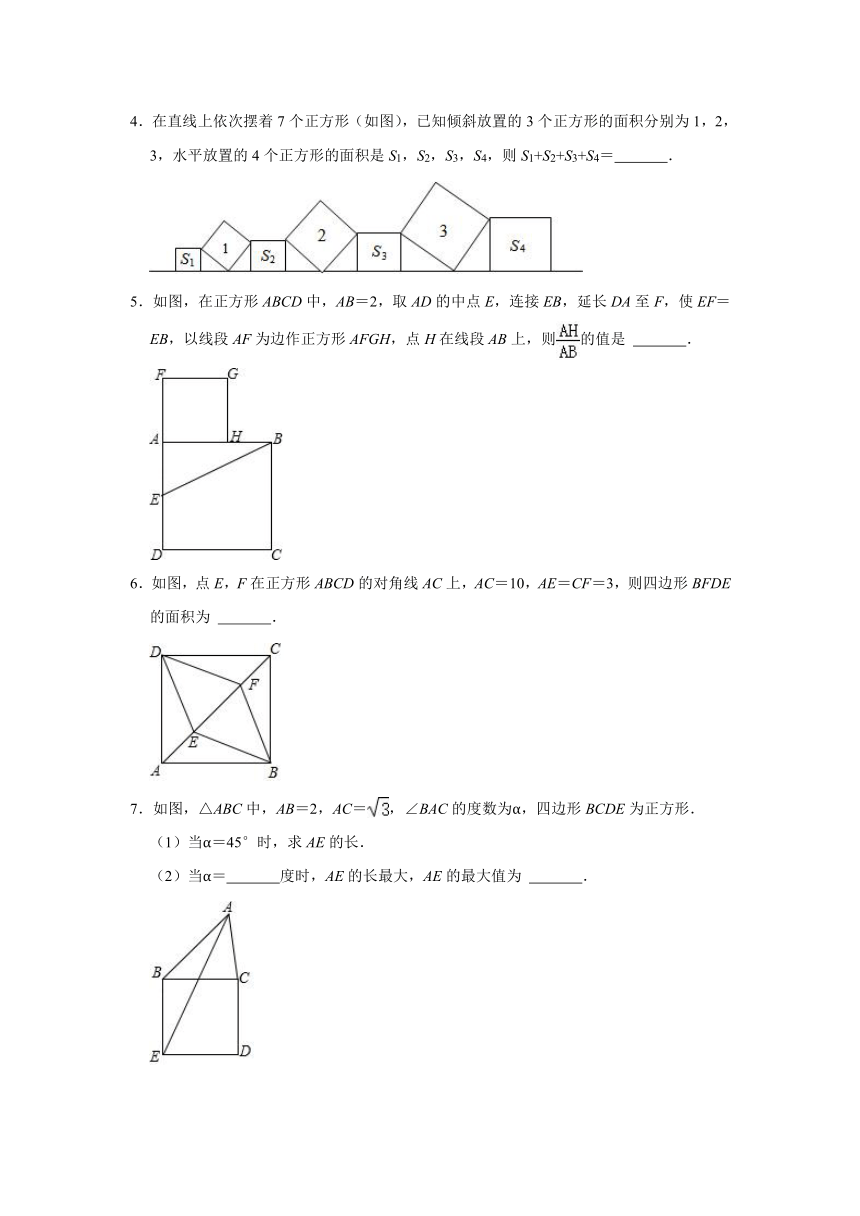
1.如图,已知在正方形ABCD中,AB=BC=CD=AD=10厘米,∠A=∠B=∠C=∠D=90°,点E在边AB上,且AE=4厘米,如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动,设运动时间为t秒.当△BPE与△CQP全等时,t的值为( )
A.2 B.2或1.5 C.2.5 D.2.5或2
2.如图,正方形ABCD的对角线AC,BD交于点O,M是边AD上一点,连接OM,过点O作ON⊥OM,交CD于点N.若四边形MOND的面积是1,则AB的长为( )
A.1 B. C.2 D.2
3.如图,在Rt△ABC中,∠ACB=90°,BC=6,AC=8,里面放置两个大小相同的正方形CDEF与正方形GHIJ,点F在边BC上,点D,H在边AC上,点G在边DE上,点I,J在斜边AB上,则正方形CDEF的边长为( )
A. B. C. D.
4.在直线上依次摆着7个正方形(如图),已知倾斜放置的3个正方形的面积分别为1,2,3,水平放置的4个正方形的面积是S1,S2,S3,S4,则S1+S2+S3+S4= .
5.如图,在正方形ABCD中,AB=2,取AD的中点E,连接EB,延长DA至F,使EF=EB,以线段AF为边作正方形AFGH,点H在线段AB上,则的值是 .
6.如图,点E,F在正方形ABCD的对角线AC上,AC=10,AE=CF=3,则四边形BFDE的面积为 .
7.如图,△ABC中,AB=2,AC=,∠BAC的度数为α,四边形BCDE为正方形.
(1)当α=45°时,求AE的长.
(2)当α= 度时,AE的长最大,AE的最大值为 .
8.如图,在正方形ABCD中,点E在边BC上,连接AE,∠DAE的平分线AG与边CD相交于点G,与BC的延长线相交于点F.
(1)若AB=2,BE=CE,求CF的长.
(2)连接EG,若EG⊥AF,求证:G为边CD的中点.
二.正方形的判定
9.已知四边形ABCD是平行四边形,下列结论中不正确的是( )
A.当AC=BD时,四边形ABCD是正方形
B.当AC⊥BD时,四边形ABCD是菱形
C.当AB=BC时,四边形ABCD是菱形
D.当∠ABC=90°时,四边形ABCD是矩形
10.下列说法正确的是( )
A.对角线相等的四边形是矩形
B.对角线互相垂直且相等的四边形是正方形
C.对角线互相垂直平分的四边形是菱形
D.四边相等的四边形是正方形
11.如图,Rt△ABC≌Rt△DCB,其中∠ABC=90°,AB=3,BC=4,O为BC中点,EF过点O分别交AC、BD于点E、F,连接BE、CF,有以下四个结论:①四边形BECF为平行四边形;②当BF=3.5时,四边形BECF为矩形;③当BF=2.5时,四边形BECF为菱形;④四边形BECF不可能为正方形.其中错误的结论是 .(填写序号)
12.如图,在△ABC中,DE∥CA,DF∥BA,下列说法:①如果∠BAC=90°,那么四边形AEDF是矩形;②如果AD平分∠BAC,那么四边形AEDF是菱形;③如果AD⊥BC且AB=AC,那么四边形AEDF是正方形.其中正确的有 个.
13.如图,在矩形ABCD中,AB=6,BC=8.如果E、F分别是AD、BC上的点,且EF经过AC中点O,G,H是对角线AC上的点.下列判断正确的有 .(填序号)
①在AC上存在无数组G、H,使得四边形EGFH是平行四边形;
②在AC上存在无数组G、H,使得四边形EGFH是矩形;
③在AC上存在无数组G、H,使得四边形EGFH是菱形;
④当AG=时,存在E、F、H,使得四边形EGFH是正方形.
14.已知,为矩形的对角线,完成如下操作,并解决问题:
(1)作的垂直平分线;(不写画法,保留作图痕迹)
(2)在直线上确定两点,,使四边形为正方形,简要阐述作法,并说明理由.
15.如图,在平面直角坐标系xOy中,直线OC:yOC=3x与直线AC:yAC=﹣x+8相交于点C(2,6).
(1)点M从点O出发以每秒1个单位长度的速度沿x轴向右运动,点N从点A出发以每秒3个单位长度的速度沿x轴向左运动,两点同时出发.分别过点M,N作x轴的垂线,分别交直线OC,AC于点P,Q,请你在图1中画出图形,猜想四边形PMNQ的形状(点M,N重合时除外),并证明你的猜想;
(2)在(1)的条件下,当点M运动 秒时,四边形PMNQ是正方形(直接写出结论).
16.如图,△ABC中,AB=AC,D、F分别为BC、AC的中点,连接DF并延长到点E,使DF=FE,连接AE、AD、CE.
(1)求证:四边形AECD是矩形.
(2)当△ABC满足什么条件时,四边形AECD是正方形,并说明理由.
三.正方形的判定与性质
17.如图,点D,E,F分别是△ABC三边的中点,则下列判断:
①四边形AEDF一定是平行四边形;
②若AD平分∠A,则四边形AEDF是正方形;
③若AD⊥BC,则四边形AEDF是菱形;
④若∠A=90°,则四边形AEDF是矩形.
正确的个数为( )
A.1 B.2 C.3 D.4
18.如图,在平面直角坐标系xOy中,P(4,4),A、B分别是x轴正半轴、y轴正半轴上的动点,且△ABO的周长是8,则P到直线AB的距离是( )
A.4 B.3 C.2.5 D.2
19.如图,分别以点A、B为圆心,同样长度为半径作圆弧,两弧相交于点C、D.连结AC、BC、AD、BD,则四边形ADBC一定是 .
A.矩形 B.菱形 C.正方形 D.平行四边形
20.如图,以平行四边形ABCD的边AB、BC、CD、DA为斜边,分别向外侧作等腰直角三角形,直角顶点分别为E、F、G、H,顺次连接这四个点,得四边形EFGH,当∠ADC=α(0°<α<90°)时,有以下结论:①∠GCF=180°﹣α;②∠HAE=90°+α;③HE=HG;④四边形EFGH是正方形;⑤四边形EFGH是菱形.则结论正确有 .
21.如图,在正方形ABCD中,E,F,G,H分别在它的四条边上,且AE=BF=CG=DH.四边形EFGH是什么特殊四边形?你是如何判断的?
22.如图,Rt△CEF中,∠C=90°,∠CEF,∠CFE外角平分线交于点A,过点A分别作直线CE,CF的垂线,B,D为垂足.
(1)求证:四边形ABCD是正方形.
(2)已知AB的长为6,求(BE+6)(DF+6)的值.
(3)借助于上面问题的解题思路,解决下列问题:若三角形PQR中,∠QPR=45°,一条高是PH,长度为6,QH=2,求HR长度.
参考答案
一.正方形的性质
1.解:当点Q的运动速度与点P的运动速度都是2厘米/秒,若△BPE≌△CQP,则BP=CQ,BE=CP,
∵AB=BC=10厘米,AE=4厘米,
∴BE=CP=6厘米,
∴BP=10﹣6=4厘米,
∴运动时间=4÷2=2(秒);
当点Q的运动速度与点P的运动速度不相等,
∴BP≠CQ,
∵∠B=∠C=90°,
∴要使△BPE与△OQP全等,只要BP=PC=5厘米,CQ=BE=6厘米,即可.
∴点P,Q运动的时间t==(秒),
故选:D.
2.解:∵四边形ABCD是正方形,
∴∠MDO=∠NCO=45°,OD=OC,∠DOC=90°,
∴∠DON+∠CON=90°,
∵ON⊥OM,
∴∠MON=90°,
∴∠DON+∠DOM=90°,
∴∠DOM=∠CON,
在△DOM和△CON中,
,
∴△DOM≌△CON(ASA),
∵四边形MOND的面积是1,四边形MOND的面积=△DOM的面积+△DON的面积,
∴四边形MOND的面积=△CON的面积+△DON的面积=△DOC的面积,
∴△DOC的面积是1,
∴正方形ABCD的面积是4,
∴AB2=4,
∴AB=2,
故选:C.
3.解:在Rt△ABC中,
∵∠ACB=90°,BC=6,AC=8,
∴AB==10.
∵四边形GHIJ为正方形,
∴GH∥AB.
∴∠GHD=∠A.
设正方形CDEF与正方形GHIJ的边长为x,则HI=CD=x.
在Rt△AHI中,
∴.
∴AH=x.
在Rt△GHD中,
∴DH=x.
∵AC=CD+DH+AH=8,
∴x+x+x=8.
解得:x=.
故选:B.
4.解:如图,∵图中的四边形为正方形,
∴∠ABD=90°,AB=DB,
∴∠ABC+∠DBE=90°,
∵∠ABC+∠CAB=90°,
∴∠CAB=∠DBE,
在△ABC和△BDE中,
,
∴△ABC≌△BDE(AAS),
∴AC=BE,
∵DE2+BE2=BD2,
∴ED2+AC2=BD2,
∵S1=AC2,S2=DE2,BD2=1,
∴S1+S2=1,
同理可得S3+S4=3,
∴S1+S2+S3+S4=1+3=4.
故答案为4.
5.解:设AB=2a,
∵四边形ABCD为正方形,
∴AD=AB=2a,∠BAD=90°,
∵E点为AD的中点,
∴AE=a,
∴BE===a,
∴EF=BE=a,
∴AF=EF﹣AE=(﹣1)a,
∵四边形AFGH为正方形,
∴AH=AF=(﹣1)a,
∴==,
故答案为:.
6.解:连接BD交AC于点O,
∵四边形ABCD为正方形,
∴OA=OB=OC=OD,AC⊥BD,
又∵AE=CF,
∴OE=OF,
∴四边形BEDF为平行四边形,
∵EF垂直平分BD,
∴EB=ED,
∴四边形BEDF是菱形,
∴BD=AC=10,
∵AE=CF=3,
∴EF=4,
∴四边形BFDE的面积为BD EF=×10×4=20.
故答案为:20.
7.解:(1)以AB为边,在AB的左侧作正方形ABMN,连接MC、AM,则AB=BM,∠ABM=90°,∠MAB=45°,
∵AB=2,
∴AM=2,
∵四边形BCDE为正方形,
∴BC=BE,∠CBE=90°,
∴∠MBC=∠ABE,
∴△MBC≌△ABE,
∴MC=AE,
∵α=45°,∠MAB=45°,
∴∠MAC=∠MAB+∠BAC=90°,
∵AC=,AM=2,
∴MC==,
∴AE=.
(2)结合图1可知,当M、A、C三点共线时,MC的长最大,即AE的长最大,
∴AE=MC=MA+AC=2+,
此时,∠MAC=180°,∠MAB=45°,
∴∠BAC=180°﹣45°=135°,即α=135°.
故答案为:135,2+.
8.解:(1)∵四边形ABCD为正方形,
∴AD∥BC,
∴∠DAG=∠F,
又∵AG平分∠DAE,
∴∠DAG=∠EAG,
∴∠EAG=∠F,
∴EA=EF,
∵AB=2,BE=CE,
∴BE=EC=1,
∵四边形ABCD为正方形,
∴∠B=90°,
在Rt△ABE中,由勾股定理得,
AE==,
∴EF=,
∴CF=EF﹣EC=﹣1;
(2)证明:∵EA=EF,EG⊥AF,
∴AG=FG,
在△ADG和△FCG中
,
∴△ADG≌△FCG(AAS),
∴DG=CG,
即点G为CD的中点.
二.正方形的判定
9.解:A.当AC=BD时,由对角线相等的平行四边形是矩形,故该选项不符合题意;
B.当AC⊥BD时,由对角线互相垂直的平行四边形是菱形可得四边形ABCD是菱形,故该选项不符合题意;
C.当AB=BC时,由一组邻边相等的平行四边形是菱形可得四边形ABCD是菱形,故该选项不符合题意;
D.当∠ABC=90°时,由有一个角为直角的平行四边形是矩形可得四边形ABCD是矩形,故该选项不符合题意;
故选:A.
10.解:A、对角线平分且相等的四边形是矩形,说法错误,不符合题意;
B、对角线平分互相垂直且相等的四边形是正方形,说法错误,不符合题意;
C、对角线互相垂直平分的四边形是菱形,说法正确,符合题意;
D、四边相等的四边形是菱形,说法错误,不符合题意;
故选:C.
11.解:∵∠ABC=90°,AB=3,BC=4,
∴AC==5,
∵Rt△ABC≌Rt△DCB,
∴AB=CD=3,AC=BD=5,BC=EF=4,∠A=∠D,∠ACB=∠CBD,∠ABC=∠DCB=90°,
∵O为BC中点,
∴BO=CO,
在△BOF和△COE中,
,
∴△BOF≌△COE(ASA),
∴OF=OE,
∴四边形BECF为平行四边形,故①正确;
当BF=3.5时,若BE⊥AC,
∵,
∴BE=,
∴,
∵BF=3.5,
∴CE≠BF,
∴BF=3.5时,四边形BECF不是矩形,
故②错误,
∵BF=2.5,
∴CE=2.5,
∴AE=AC﹣CE=2.5,
∴E为AC中点,
∴BE=CE,
∵四边形BECF是平行四边形,
∴当BF=2.5时,四边形BECF为菱形,故③正确;
当BF=2.5时,四边形BECF为菱形,此时∠BEC≠90°,
∴四边形BECF不可能为正方形.故④正确.
故答案为:②.
12.解:①∵DE∥CA,DF∥BA,
∴四边形AEDF是平行四边形,
∵∠BAC=90°,
∴平行四边形AEDF是矩形,故①正确;
②∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵DF∥AB,
∴∠ADF=∠BAD,
∴∠ADF=∠CAD,
∴AF=DF,
∵四边形AEDF是平行四边形,
∴四边形AEDF是菱形,故②正确;
③∵AD⊥BC,AC=AB,
∴AD平分∠BAC,
∴∠BAD=∠CAD,
∵DF∥AB,
∴∠ADF=∠BAD,
∴∠ADF=∠CAD,
∴AF=DF,
∵四边形AEDF是平行四边形,
∴四边形AEDF是菱形,四边形AEDF不一定是正方形,故③错误;
即正确的个数是2个,
故答案为:2.
13.解:①在AC上存在无数组G,H,使得四边形EGFH是平行四边形,故该说法正确;
②在AC上存在无数组G,H,使得四边形EGFH是矩形,故该说法正确;
③在AC上存在无数组G,H,使得四边形EGFH是菱形,故该说法正确;
④当AG=时,存在E、F、H,使得四边形EGFH是正方形,
故答案为①②③④.
14.(1)解:直线如图所示
(2)解:正方形如图所示,
设直线与的交点为O,以O为圆心,的长度为半径画弧,交直线于两点M、N,连接,,,,
∵且,
∴四边形是正方形.
15.解:(1)如图,四边形PMNQ为矩形,
证明:∵点A在直线AC:yAC=﹣x+8上,
当y=0 时,x=8,
∴A(8,0),
设点M的运动时间为m秒,
则OM=m,AN=3m,
∴M(m,0),N(8﹣3m,0),
∵PM⊥x轴,QN⊥x轴,
∴∠PMA=∠QNA=90°,
∴PM∥QN,
∵点P在直线OC:yOC=3x,点Q在直线AC:yAC=﹣x+8上,
∴P(m,3m),Q(8﹣3m,3m),
∴PM=QN,
∴四边形PMNQ为平行四边形,
∵∠PMA=90°,
∴四边形PMNQ为矩形;
(2)∵四边形PMNQ是正方形,
∴MN=QN,
即8﹣4m=|3m|,
解得:x=或8,
∴当点M运动秒或8秒时,四边形PMNQ是正方形,
故答案为:或8.
16.证明:(1)∵D、F分别为BC、AC的中点,使DF=FE,
∴CF=FA,
∴四边形AECD是平行四边形,
∵AB=AC,AD是△ABC的角平分线,
∴AD⊥BC,
∴∠ADC=90°,
∴平行四边形AECD是矩形;
(2)当∠BAC=90°时,
理由:∵∠BAC=90°,AB=AC,AD是△ABC的角平分线,
∴AD=BD=CD,
∵由(1)得四边形AECD是矩形,
∴矩形AECD是正方形.
三.正方形的判定与性质
17.解:①∵D是BC的中点,E是AB的中点,
∴DE∥AC.
∵D是BC的中点,F是AC的中点,
∴DF∥AB.
∴四边形AEDF是平行四边形.
∴①正确;
②如图,
由①知:AE∥DF,
∴∠EAD=∠ADF.
若AD平分∠BAC,
则∠EAD=∠FAD.
∴∠FAD=∠ADF,
∴AF=FD,
∵四边形AEDF是平行四边形,
∴四边形AEDF是菱形.
∴②不正确;
③如图,
若AD⊥BC,
∵D是BC的中点,
∴AD是BC的垂直平分线,
∴AB=AC.
∵AD⊥BC,E是AB的中点,
∴DE=AB.
同理:DF=AC,
∴DE=DF.
由①知:四边形AEDF是平行四边形,
∴四边形AEDF是菱形.
∴③正确;
④若∠A=90°,如图,
由①知:四边形AEDF是平行四边形,
∵∠A=90°,
∴四边形AEDF是矩形,
∴④正确;
综上可得,正确的结论有:①③④,
故选:C.
18.解:如图,过点P作PC⊥x轴,PD⊥y轴,垂直分别为C,D,
∵P(4,4),
∴四边形CODP是边长为4的正方形,
∴PC=PD=OC=OD=4,
将△PAD沿PA折叠得到△PAE,延长AE交y轴于点B,
∴PE=PD,AD=AE,∠PDA=∠PEA=90°,
∴PE=PC,
在Rt△PEB和Rt△PCB中,
,
∴Rt△PEB≌Rt△PCB(HL),
∴BE=BC,
∵△ABO的周长是8,
∴AO+BO+AE=AO+BO+BE+AE=AO+BO+BC+AD=CO+DO=8,
∴△ABO符合题意,
∴P到直线AB的距离PE=4,
故选:A.
19.解:由题意可知:AC=AD=BC=BD,
∴四边形ADBC是菱形,也是平行四边形,
故答案为:BD.
20.解:∵四边形ABCD是平行四边形,
∴∠ABC=∠ADC=α,∠BAD=∠BCD,AB=CD,AD=BC,AD∥BC,AB∥CD,
∵平行四边形ABCD的边AB、BC、CD、DA为斜边,分别向外侧作等腰直角三角形,直角顶点分别为E、F、G、H,
∴BE=AE=CG=DG,AH=DH=BF=CF,∠ABE=∠EAB=∠FBC=∠FCB=∠GCD=∠GDC=∠HAD=∠HDA=45°,
∵AB∥CD,
∴∠BAD=∠BCD=180°﹣α,
∴∠EAH=360°﹣45°﹣45°﹣(180°﹣α)=90°+α,∠GCF=360°﹣45°﹣45°﹣(180°﹣α)=90°+α,
∴①错误;②正确;
∠HDG=45°+45°+α=90°+α,∠FBE=45°+45°+α=90°+α,
∴∠HAE=∠HDG=∠FCG=∠FBE,
在△FBE、△HAE、△HDG、△FCG中,
,
∴△FBE≌△HAE≌△HDG≌△FCG(SAS),
∴∠BFE=∠GFC,EF=EH=HG=GF,
∴四边形EFGH是菱形,
∵∠BFC=90°=∠BFE+∠EFC=∠GFC+∠CFE,
∴∠EFG=90°,
∴四边形EFGH是正方形,
∴②③④⑤正确;
故答案为:②③④⑤.
21.解:四边形EFGH是正方形.
证明:∵AE=BF=CG=DH,
∴AH=DG=CF=BE.
∵∠A=∠B=∠C=∠D=90°,
∴△AEH≌△DHG≌△CGF≌△BFE,
∴EF=EH=HG=GF,∠EHA=∠HGD.
∴四边形EFGH是菱形.
∵∠EHA=∠HGD,∠HGD+∠GHD=90°,
∴∠EHA+∠GHD=90°.
∴∠EHG=90°.
∴四边形EFGH是正方形.
22.(1)证明:作AG⊥EF于G,如图1,
则∠AGE=∠AGF=90°,
∵AB⊥CE,AD⊥CF,
∴∠B=∠D=90°=∠C,
∴四边形ABCD是矩形,
∵∠CEF,∠CFE外角平分线交于点A,
∴AB=AG,AD=AG,
∴AB=AD,
∴四边形ABCD是正方形;
(2)解:∵四边形ABCD是正方形,
∴BC=CD=6,
在Rt△ABE和Rt△AGE中,
,
∴Rt△ABE≌Rt△AGE(HL),
∴BE=BG,
同理:Rt△ADF≌Rt△AGF(HL),
∴DF=GF,∴BE+DF=GE+GF=EF,
设BE=x,DF=y,则CE=BC﹣BE=6﹣x,CF=CD﹣DF=6﹣y,EF=x+y,
在Rt△CEF中,由勾股定理得:(6﹣x)2+(6﹣y)2=(x+y)2,
整理得:xy+6(x+y)=36,
∴(BE+6)(DF+6)=(x+6)(y+6)=xy+6(x+y)+36=36+36=72;
(3)解:如图2所示:
把△PQH沿PQ翻折得△PQD,把△PRH沿PR翻折得△PRM,延长DQ、MR交于点G,
由(1)(2)得:四边形PMGD是正方形,MR+DQ=QR,MR=HR,DQ=HQ=2,
∴MG=DG=MP=PH=6,
∴GQ=4,
设MR=HR=a,则GR=6﹣a,QR=a+2,
在Rt△GQR中,由勾股定理得:(6﹣a)2+42=(2+a)2,
解得:a=3,即HR=3.
当△PQR是钝角三角形时,过P作PT⊥PR交RQ延长线于T,如图3所示:
则∠TPQ=90°﹣45°=45°,
由①得:TH=3,
∴PT===3,
设HR=x,PR=y,则TR=x+3,
∵△PTR的面积=(x+3)×6=×3y,
∴y=6+2x,
∴5y2=(6+2x)2①,
在Rt△PRH中,由勾股定理得:y2=62+x2②,
由①②得:(x﹣12)2=0,
∴x=12,
即HR=12;
综上所述,HR为3或12,
同步知识点分类练习题(附答案)
一.正方形的性质
1.如图,已知在正方形ABCD中,AB=BC=CD=AD=10厘米,∠A=∠B=∠C=∠D=90°,点E在边AB上,且AE=4厘米,如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动,设运动时间为t秒.当△BPE与△CQP全等时,t的值为( )
A.2 B.2或1.5 C.2.5 D.2.5或2
2.如图,正方形ABCD的对角线AC,BD交于点O,M是边AD上一点,连接OM,过点O作ON⊥OM,交CD于点N.若四边形MOND的面积是1,则AB的长为( )
A.1 B. C.2 D.2
3.如图,在Rt△ABC中,∠ACB=90°,BC=6,AC=8,里面放置两个大小相同的正方形CDEF与正方形GHIJ,点F在边BC上,点D,H在边AC上,点G在边DE上,点I,J在斜边AB上,则正方形CDEF的边长为( )
A. B. C. D.
4.在直线上依次摆着7个正方形(如图),已知倾斜放置的3个正方形的面积分别为1,2,3,水平放置的4个正方形的面积是S1,S2,S3,S4,则S1+S2+S3+S4= .
5.如图,在正方形ABCD中,AB=2,取AD的中点E,连接EB,延长DA至F,使EF=EB,以线段AF为边作正方形AFGH,点H在线段AB上,则的值是 .
6.如图,点E,F在正方形ABCD的对角线AC上,AC=10,AE=CF=3,则四边形BFDE的面积为 .
7.如图,△ABC中,AB=2,AC=,∠BAC的度数为α,四边形BCDE为正方形.
(1)当α=45°时,求AE的长.
(2)当α= 度时,AE的长最大,AE的最大值为 .
8.如图,在正方形ABCD中,点E在边BC上,连接AE,∠DAE的平分线AG与边CD相交于点G,与BC的延长线相交于点F.
(1)若AB=2,BE=CE,求CF的长.
(2)连接EG,若EG⊥AF,求证:G为边CD的中点.
二.正方形的判定
9.已知四边形ABCD是平行四边形,下列结论中不正确的是( )
A.当AC=BD时,四边形ABCD是正方形
B.当AC⊥BD时,四边形ABCD是菱形
C.当AB=BC时,四边形ABCD是菱形
D.当∠ABC=90°时,四边形ABCD是矩形
10.下列说法正确的是( )
A.对角线相等的四边形是矩形
B.对角线互相垂直且相等的四边形是正方形
C.对角线互相垂直平分的四边形是菱形
D.四边相等的四边形是正方形
11.如图,Rt△ABC≌Rt△DCB,其中∠ABC=90°,AB=3,BC=4,O为BC中点,EF过点O分别交AC、BD于点E、F,连接BE、CF,有以下四个结论:①四边形BECF为平行四边形;②当BF=3.5时,四边形BECF为矩形;③当BF=2.5时,四边形BECF为菱形;④四边形BECF不可能为正方形.其中错误的结论是 .(填写序号)
12.如图,在△ABC中,DE∥CA,DF∥BA,下列说法:①如果∠BAC=90°,那么四边形AEDF是矩形;②如果AD平分∠BAC,那么四边形AEDF是菱形;③如果AD⊥BC且AB=AC,那么四边形AEDF是正方形.其中正确的有 个.
13.如图,在矩形ABCD中,AB=6,BC=8.如果E、F分别是AD、BC上的点,且EF经过AC中点O,G,H是对角线AC上的点.下列判断正确的有 .(填序号)
①在AC上存在无数组G、H,使得四边形EGFH是平行四边形;
②在AC上存在无数组G、H,使得四边形EGFH是矩形;
③在AC上存在无数组G、H,使得四边形EGFH是菱形;
④当AG=时,存在E、F、H,使得四边形EGFH是正方形.
14.已知,为矩形的对角线,完成如下操作,并解决问题:
(1)作的垂直平分线;(不写画法,保留作图痕迹)
(2)在直线上确定两点,,使四边形为正方形,简要阐述作法,并说明理由.
15.如图,在平面直角坐标系xOy中,直线OC:yOC=3x与直线AC:yAC=﹣x+8相交于点C(2,6).
(1)点M从点O出发以每秒1个单位长度的速度沿x轴向右运动,点N从点A出发以每秒3个单位长度的速度沿x轴向左运动,两点同时出发.分别过点M,N作x轴的垂线,分别交直线OC,AC于点P,Q,请你在图1中画出图形,猜想四边形PMNQ的形状(点M,N重合时除外),并证明你的猜想;
(2)在(1)的条件下,当点M运动 秒时,四边形PMNQ是正方形(直接写出结论).
16.如图,△ABC中,AB=AC,D、F分别为BC、AC的中点,连接DF并延长到点E,使DF=FE,连接AE、AD、CE.
(1)求证:四边形AECD是矩形.
(2)当△ABC满足什么条件时,四边形AECD是正方形,并说明理由.
三.正方形的判定与性质
17.如图,点D,E,F分别是△ABC三边的中点,则下列判断:
①四边形AEDF一定是平行四边形;
②若AD平分∠A,则四边形AEDF是正方形;
③若AD⊥BC,则四边形AEDF是菱形;
④若∠A=90°,则四边形AEDF是矩形.
正确的个数为( )
A.1 B.2 C.3 D.4
18.如图,在平面直角坐标系xOy中,P(4,4),A、B分别是x轴正半轴、y轴正半轴上的动点,且△ABO的周长是8,则P到直线AB的距离是( )
A.4 B.3 C.2.5 D.2
19.如图,分别以点A、B为圆心,同样长度为半径作圆弧,两弧相交于点C、D.连结AC、BC、AD、BD,则四边形ADBC一定是 .
A.矩形 B.菱形 C.正方形 D.平行四边形
20.如图,以平行四边形ABCD的边AB、BC、CD、DA为斜边,分别向外侧作等腰直角三角形,直角顶点分别为E、F、G、H,顺次连接这四个点,得四边形EFGH,当∠ADC=α(0°<α<90°)时,有以下结论:①∠GCF=180°﹣α;②∠HAE=90°+α;③HE=HG;④四边形EFGH是正方形;⑤四边形EFGH是菱形.则结论正确有 .
21.如图,在正方形ABCD中,E,F,G,H分别在它的四条边上,且AE=BF=CG=DH.四边形EFGH是什么特殊四边形?你是如何判断的?
22.如图,Rt△CEF中,∠C=90°,∠CEF,∠CFE外角平分线交于点A,过点A分别作直线CE,CF的垂线,B,D为垂足.
(1)求证:四边形ABCD是正方形.
(2)已知AB的长为6,求(BE+6)(DF+6)的值.
(3)借助于上面问题的解题思路,解决下列问题:若三角形PQR中,∠QPR=45°,一条高是PH,长度为6,QH=2,求HR长度.
参考答案
一.正方形的性质
1.解:当点Q的运动速度与点P的运动速度都是2厘米/秒,若△BPE≌△CQP,则BP=CQ,BE=CP,
∵AB=BC=10厘米,AE=4厘米,
∴BE=CP=6厘米,
∴BP=10﹣6=4厘米,
∴运动时间=4÷2=2(秒);
当点Q的运动速度与点P的运动速度不相等,
∴BP≠CQ,
∵∠B=∠C=90°,
∴要使△BPE与△OQP全等,只要BP=PC=5厘米,CQ=BE=6厘米,即可.
∴点P,Q运动的时间t==(秒),
故选:D.
2.解:∵四边形ABCD是正方形,
∴∠MDO=∠NCO=45°,OD=OC,∠DOC=90°,
∴∠DON+∠CON=90°,
∵ON⊥OM,
∴∠MON=90°,
∴∠DON+∠DOM=90°,
∴∠DOM=∠CON,
在△DOM和△CON中,
,
∴△DOM≌△CON(ASA),
∵四边形MOND的面积是1,四边形MOND的面积=△DOM的面积+△DON的面积,
∴四边形MOND的面积=△CON的面积+△DON的面积=△DOC的面积,
∴△DOC的面积是1,
∴正方形ABCD的面积是4,
∴AB2=4,
∴AB=2,
故选:C.
3.解:在Rt△ABC中,
∵∠ACB=90°,BC=6,AC=8,
∴AB==10.
∵四边形GHIJ为正方形,
∴GH∥AB.
∴∠GHD=∠A.
设正方形CDEF与正方形GHIJ的边长为x,则HI=CD=x.
在Rt△AHI中,
∴.
∴AH=x.
在Rt△GHD中,
∴DH=x.
∵AC=CD+DH+AH=8,
∴x+x+x=8.
解得:x=.
故选:B.
4.解:如图,∵图中的四边形为正方形,
∴∠ABD=90°,AB=DB,
∴∠ABC+∠DBE=90°,
∵∠ABC+∠CAB=90°,
∴∠CAB=∠DBE,
在△ABC和△BDE中,
,
∴△ABC≌△BDE(AAS),
∴AC=BE,
∵DE2+BE2=BD2,
∴ED2+AC2=BD2,
∵S1=AC2,S2=DE2,BD2=1,
∴S1+S2=1,
同理可得S3+S4=3,
∴S1+S2+S3+S4=1+3=4.
故答案为4.
5.解:设AB=2a,
∵四边形ABCD为正方形,
∴AD=AB=2a,∠BAD=90°,
∵E点为AD的中点,
∴AE=a,
∴BE===a,
∴EF=BE=a,
∴AF=EF﹣AE=(﹣1)a,
∵四边形AFGH为正方形,
∴AH=AF=(﹣1)a,
∴==,
故答案为:.
6.解:连接BD交AC于点O,
∵四边形ABCD为正方形,
∴OA=OB=OC=OD,AC⊥BD,
又∵AE=CF,
∴OE=OF,
∴四边形BEDF为平行四边形,
∵EF垂直平分BD,
∴EB=ED,
∴四边形BEDF是菱形,
∴BD=AC=10,
∵AE=CF=3,
∴EF=4,
∴四边形BFDE的面积为BD EF=×10×4=20.
故答案为:20.
7.解:(1)以AB为边,在AB的左侧作正方形ABMN,连接MC、AM,则AB=BM,∠ABM=90°,∠MAB=45°,
∵AB=2,
∴AM=2,
∵四边形BCDE为正方形,
∴BC=BE,∠CBE=90°,
∴∠MBC=∠ABE,
∴△MBC≌△ABE,
∴MC=AE,
∵α=45°,∠MAB=45°,
∴∠MAC=∠MAB+∠BAC=90°,
∵AC=,AM=2,
∴MC==,
∴AE=.
(2)结合图1可知,当M、A、C三点共线时,MC的长最大,即AE的长最大,
∴AE=MC=MA+AC=2+,
此时,∠MAC=180°,∠MAB=45°,
∴∠BAC=180°﹣45°=135°,即α=135°.
故答案为:135,2+.
8.解:(1)∵四边形ABCD为正方形,
∴AD∥BC,
∴∠DAG=∠F,
又∵AG平分∠DAE,
∴∠DAG=∠EAG,
∴∠EAG=∠F,
∴EA=EF,
∵AB=2,BE=CE,
∴BE=EC=1,
∵四边形ABCD为正方形,
∴∠B=90°,
在Rt△ABE中,由勾股定理得,
AE==,
∴EF=,
∴CF=EF﹣EC=﹣1;
(2)证明:∵EA=EF,EG⊥AF,
∴AG=FG,
在△ADG和△FCG中
,
∴△ADG≌△FCG(AAS),
∴DG=CG,
即点G为CD的中点.
二.正方形的判定
9.解:A.当AC=BD时,由对角线相等的平行四边形是矩形,故该选项不符合题意;
B.当AC⊥BD时,由对角线互相垂直的平行四边形是菱形可得四边形ABCD是菱形,故该选项不符合题意;
C.当AB=BC时,由一组邻边相等的平行四边形是菱形可得四边形ABCD是菱形,故该选项不符合题意;
D.当∠ABC=90°时,由有一个角为直角的平行四边形是矩形可得四边形ABCD是矩形,故该选项不符合题意;
故选:A.
10.解:A、对角线平分且相等的四边形是矩形,说法错误,不符合题意;
B、对角线平分互相垂直且相等的四边形是正方形,说法错误,不符合题意;
C、对角线互相垂直平分的四边形是菱形,说法正确,符合题意;
D、四边相等的四边形是菱形,说法错误,不符合题意;
故选:C.
11.解:∵∠ABC=90°,AB=3,BC=4,
∴AC==5,
∵Rt△ABC≌Rt△DCB,
∴AB=CD=3,AC=BD=5,BC=EF=4,∠A=∠D,∠ACB=∠CBD,∠ABC=∠DCB=90°,
∵O为BC中点,
∴BO=CO,
在△BOF和△COE中,
,
∴△BOF≌△COE(ASA),
∴OF=OE,
∴四边形BECF为平行四边形,故①正确;
当BF=3.5时,若BE⊥AC,
∵,
∴BE=,
∴,
∵BF=3.5,
∴CE≠BF,
∴BF=3.5时,四边形BECF不是矩形,
故②错误,
∵BF=2.5,
∴CE=2.5,
∴AE=AC﹣CE=2.5,
∴E为AC中点,
∴BE=CE,
∵四边形BECF是平行四边形,
∴当BF=2.5时,四边形BECF为菱形,故③正确;
当BF=2.5时,四边形BECF为菱形,此时∠BEC≠90°,
∴四边形BECF不可能为正方形.故④正确.
故答案为:②.
12.解:①∵DE∥CA,DF∥BA,
∴四边形AEDF是平行四边形,
∵∠BAC=90°,
∴平行四边形AEDF是矩形,故①正确;
②∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵DF∥AB,
∴∠ADF=∠BAD,
∴∠ADF=∠CAD,
∴AF=DF,
∵四边形AEDF是平行四边形,
∴四边形AEDF是菱形,故②正确;
③∵AD⊥BC,AC=AB,
∴AD平分∠BAC,
∴∠BAD=∠CAD,
∵DF∥AB,
∴∠ADF=∠BAD,
∴∠ADF=∠CAD,
∴AF=DF,
∵四边形AEDF是平行四边形,
∴四边形AEDF是菱形,四边形AEDF不一定是正方形,故③错误;
即正确的个数是2个,
故答案为:2.
13.解:①在AC上存在无数组G,H,使得四边形EGFH是平行四边形,故该说法正确;
②在AC上存在无数组G,H,使得四边形EGFH是矩形,故该说法正确;
③在AC上存在无数组G,H,使得四边形EGFH是菱形,故该说法正确;
④当AG=时,存在E、F、H,使得四边形EGFH是正方形,
故答案为①②③④.
14.(1)解:直线如图所示
(2)解:正方形如图所示,
设直线与的交点为O,以O为圆心,的长度为半径画弧,交直线于两点M、N,连接,,,,
∵且,
∴四边形是正方形.
15.解:(1)如图,四边形PMNQ为矩形,
证明:∵点A在直线AC:yAC=﹣x+8上,
当y=0 时,x=8,
∴A(8,0),
设点M的运动时间为m秒,
则OM=m,AN=3m,
∴M(m,0),N(8﹣3m,0),
∵PM⊥x轴,QN⊥x轴,
∴∠PMA=∠QNA=90°,
∴PM∥QN,
∵点P在直线OC:yOC=3x,点Q在直线AC:yAC=﹣x+8上,
∴P(m,3m),Q(8﹣3m,3m),
∴PM=QN,
∴四边形PMNQ为平行四边形,
∵∠PMA=90°,
∴四边形PMNQ为矩形;
(2)∵四边形PMNQ是正方形,
∴MN=QN,
即8﹣4m=|3m|,
解得:x=或8,
∴当点M运动秒或8秒时,四边形PMNQ是正方形,
故答案为:或8.
16.证明:(1)∵D、F分别为BC、AC的中点,使DF=FE,
∴CF=FA,
∴四边形AECD是平行四边形,
∵AB=AC,AD是△ABC的角平分线,
∴AD⊥BC,
∴∠ADC=90°,
∴平行四边形AECD是矩形;
(2)当∠BAC=90°时,
理由:∵∠BAC=90°,AB=AC,AD是△ABC的角平分线,
∴AD=BD=CD,
∵由(1)得四边形AECD是矩形,
∴矩形AECD是正方形.
三.正方形的判定与性质
17.解:①∵D是BC的中点,E是AB的中点,
∴DE∥AC.
∵D是BC的中点,F是AC的中点,
∴DF∥AB.
∴四边形AEDF是平行四边形.
∴①正确;
②如图,
由①知:AE∥DF,
∴∠EAD=∠ADF.
若AD平分∠BAC,
则∠EAD=∠FAD.
∴∠FAD=∠ADF,
∴AF=FD,
∵四边形AEDF是平行四边形,
∴四边形AEDF是菱形.
∴②不正确;
③如图,
若AD⊥BC,
∵D是BC的中点,
∴AD是BC的垂直平分线,
∴AB=AC.
∵AD⊥BC,E是AB的中点,
∴DE=AB.
同理:DF=AC,
∴DE=DF.
由①知:四边形AEDF是平行四边形,
∴四边形AEDF是菱形.
∴③正确;
④若∠A=90°,如图,
由①知:四边形AEDF是平行四边形,
∵∠A=90°,
∴四边形AEDF是矩形,
∴④正确;
综上可得,正确的结论有:①③④,
故选:C.
18.解:如图,过点P作PC⊥x轴,PD⊥y轴,垂直分别为C,D,
∵P(4,4),
∴四边形CODP是边长为4的正方形,
∴PC=PD=OC=OD=4,
将△PAD沿PA折叠得到△PAE,延长AE交y轴于点B,
∴PE=PD,AD=AE,∠PDA=∠PEA=90°,
∴PE=PC,
在Rt△PEB和Rt△PCB中,
,
∴Rt△PEB≌Rt△PCB(HL),
∴BE=BC,
∵△ABO的周长是8,
∴AO+BO+AE=AO+BO+BE+AE=AO+BO+BC+AD=CO+DO=8,
∴△ABO符合题意,
∴P到直线AB的距离PE=4,
故选:A.
19.解:由题意可知:AC=AD=BC=BD,
∴四边形ADBC是菱形,也是平行四边形,
故答案为:BD.
20.解:∵四边形ABCD是平行四边形,
∴∠ABC=∠ADC=α,∠BAD=∠BCD,AB=CD,AD=BC,AD∥BC,AB∥CD,
∵平行四边形ABCD的边AB、BC、CD、DA为斜边,分别向外侧作等腰直角三角形,直角顶点分别为E、F、G、H,
∴BE=AE=CG=DG,AH=DH=BF=CF,∠ABE=∠EAB=∠FBC=∠FCB=∠GCD=∠GDC=∠HAD=∠HDA=45°,
∵AB∥CD,
∴∠BAD=∠BCD=180°﹣α,
∴∠EAH=360°﹣45°﹣45°﹣(180°﹣α)=90°+α,∠GCF=360°﹣45°﹣45°﹣(180°﹣α)=90°+α,
∴①错误;②正确;
∠HDG=45°+45°+α=90°+α,∠FBE=45°+45°+α=90°+α,
∴∠HAE=∠HDG=∠FCG=∠FBE,
在△FBE、△HAE、△HDG、△FCG中,
,
∴△FBE≌△HAE≌△HDG≌△FCG(SAS),
∴∠BFE=∠GFC,EF=EH=HG=GF,
∴四边形EFGH是菱形,
∵∠BFC=90°=∠BFE+∠EFC=∠GFC+∠CFE,
∴∠EFG=90°,
∴四边形EFGH是正方形,
∴②③④⑤正确;
故答案为:②③④⑤.
21.解:四边形EFGH是正方形.
证明:∵AE=BF=CG=DH,
∴AH=DG=CF=BE.
∵∠A=∠B=∠C=∠D=90°,
∴△AEH≌△DHG≌△CGF≌△BFE,
∴EF=EH=HG=GF,∠EHA=∠HGD.
∴四边形EFGH是菱形.
∵∠EHA=∠HGD,∠HGD+∠GHD=90°,
∴∠EHA+∠GHD=90°.
∴∠EHG=90°.
∴四边形EFGH是正方形.
22.(1)证明:作AG⊥EF于G,如图1,
则∠AGE=∠AGF=90°,
∵AB⊥CE,AD⊥CF,
∴∠B=∠D=90°=∠C,
∴四边形ABCD是矩形,
∵∠CEF,∠CFE外角平分线交于点A,
∴AB=AG,AD=AG,
∴AB=AD,
∴四边形ABCD是正方形;
(2)解:∵四边形ABCD是正方形,
∴BC=CD=6,
在Rt△ABE和Rt△AGE中,
,
∴Rt△ABE≌Rt△AGE(HL),
∴BE=BG,
同理:Rt△ADF≌Rt△AGF(HL),
∴DF=GF,∴BE+DF=GE+GF=EF,
设BE=x,DF=y,则CE=BC﹣BE=6﹣x,CF=CD﹣DF=6﹣y,EF=x+y,
在Rt△CEF中,由勾股定理得:(6﹣x)2+(6﹣y)2=(x+y)2,
整理得:xy+6(x+y)=36,
∴(BE+6)(DF+6)=(x+6)(y+6)=xy+6(x+y)+36=36+36=72;
(3)解:如图2所示:
把△PQH沿PQ翻折得△PQD,把△PRH沿PR翻折得△PRM,延长DQ、MR交于点G,
由(1)(2)得:四边形PMGD是正方形,MR+DQ=QR,MR=HR,DQ=HQ=2,
∴MG=DG=MP=PH=6,
∴GQ=4,
设MR=HR=a,则GR=6﹣a,QR=a+2,
在Rt△GQR中,由勾股定理得:(6﹣a)2+42=(2+a)2,
解得:a=3,即HR=3.
当△PQR是钝角三角形时,过P作PT⊥PR交RQ延长线于T,如图3所示:
则∠TPQ=90°﹣45°=45°,
由①得:TH=3,
∴PT===3,
设HR=x,PR=y,则TR=x+3,
∵△PTR的面积=(x+3)×6=×3y,
∴y=6+2x,
∴5y2=(6+2x)2①,
在Rt△PRH中,由勾股定理得:y2=62+x2②,
由①②得:(x﹣12)2=0,
∴x=12,
即HR=12;
综上所述,HR为3或12,
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
