《第1章勾股定理》同步练习题 北师大版八年级数学上册(含解析)
文档属性
| 名称 | 《第1章勾股定理》同步练习题 北师大版八年级数学上册(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 185.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-05 17:19:05 | ||
图片预览



文档简介
2023-2024学年北师大版八年级数学上册《第1章勾股定理》同步练习题(附答案)
1.下列各组数中,是勾股数的是( )
A.4,5,6 B.1,2, C.6,8,10 D.5,12,23
2.下列各组数中能作为直角三角形三边长的是( )
A.1,,2 B.3,4,5 C.4,5,6 D.13,14,15
3.已知△ABC中,a、b、c分别是∠A、∠B、∠C的对边,下列条件中不能判断△ABC是直角三角形的是( )
A.∠A:∠B:∠C=3:4:5 B.∠C=∠A﹣∠B
C.a2+b2=c2 D.a:b:c=6:8:10
4.以直角三角形的三边为边向外作正方形,其中两个正方形的面积如图所示,则正方形A的面积为( )
A.6 B.36 C.64 D.8
5.小明家需购买一张大圆桌面(不能折叠,不考虑木板厚度),若入户门的高为2.1米,宽为1.1米,则尽可能大的圆桌的直径可以是( )
A.2.45米 B.2.40米 C.2.35米 D.2.30米
6.若直角三角形的斜边长为,一条直角边长为1,则另一条直角边长为( )
A.5 B. C. D.7
7.如图,圆柱形玻璃杯,高为12cm,底面周长为18cm,在杯内离杯底4cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的A处,则蚂蚁到达蜂蜜的最短距离( )cm.
A.14 B.15 C.16 D.17
8.如图,某自动感应门的正上方A处装着一个感应器,离地AB=2.5米,当人体进入感应器的感应范围内时,感应门就会自动打开.一个身高1.6米的学生CD正对门,缓慢走到离门1.2米的地方时(BC=1.2米),感应门自动打开,则人头顶离感应器的距离AD等于( )
A.1.2米 B.1.5米 C.2.0米 D.2.5米
9.传说,古埃及人常用“拉绳”的方法画直角,有一根长为m的绳子,古埃及人用这根绳子拉出了一个斜边长为n的直角三角形,那么这个直角三角形的面积用含m和n的式子可表示为( )
A. B. C. D.
10.如图,四个全等的直角三角形和中间的小正方形可以拼成一个大正方形,若直角三角形的较长直角边长为a,较短直角边长为b,大正方形面积为S1,小正方形面积为S2,则(a+b)2可以表示为( )
A.S1﹣S2 B.S1+S2 C.2S1﹣S2 D.S1+2S2
11.在△ABC中,AB=13,BC=10,BC边上的中线AD=12,则△ABC的周长为 .
12.如图所示的网格是正方形网格,点A、B、C、D均在格点上,则∠CAB+∠CBA= °.
13.如图,“人字梯”放在水平的地面上,AB=AC,当梯子的一边与地面所夹的锐角α为60°时,两梯角之间的距离BC的长为2m.周日亮亮帮助妈妈整理换季衣服,先使α为60°,后又调整α为45°,则梯子顶端A离地面的高度下降了 m.
14.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b.若ab=4,大正方形的面积为16,则小正方形的边长为 .
15.直角三角形两直角边长分别为3和4,则它斜边上的高为 .
16.如图,由两个直角三角形和三个正方形组成的图形.其中两正方形面积分别是S1=22,S2=14,AC=10,则AB= .
17.《九章算术》是我国古代数学的经典著作.书中有一个“折竹抵地”问题:“今有竹高丈,末折抵地,问折者高几何?”意思是:一根竹子,原来高一丈(一丈为十尺),虫伤有病,一阵风将竹子折断,其竹梢恰好抵地,抵地处离原竹子根部三尺远,问:原处还有多高的竹子?
18.古希腊的哲学家柏拉图曾指出,如果m表示大于1的整数,a=2m,b=m2﹣1,c=m2+1,那么a,b,c为勾股数.你认为对吗?如果对,你能利用这个结论得出一些勾股数吗?
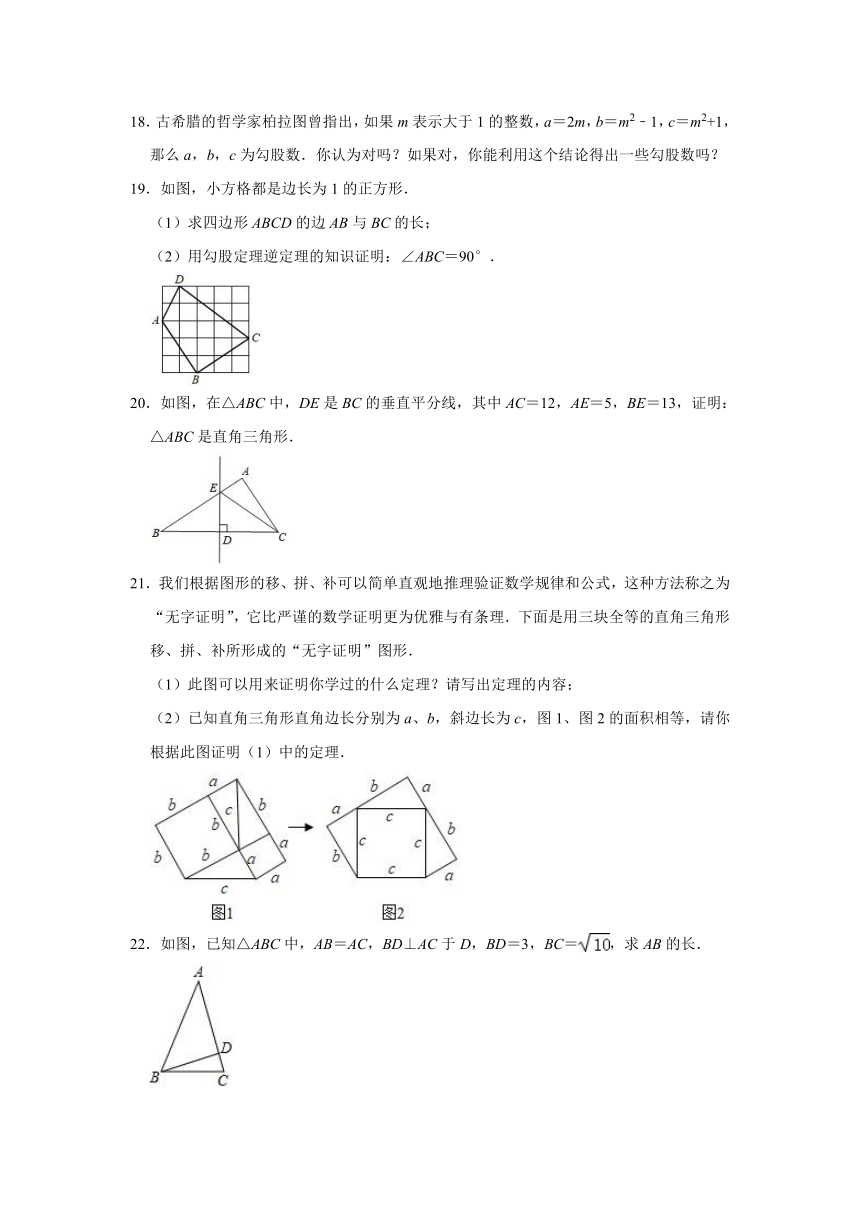
19.如图,小方格都是边长为1的正方形.
(1)求四边形ABCD的边AB与BC的长;
(2)用勾股定理逆定理的知识证明:∠ABC=90°.
20.如图,在△ABC中,DE是BC的垂直平分线,其中AC=12,AE=5,BE=13,证明:△ABC是直角三角形.
21.我们根据图形的移、拼、补可以简单直观地推理验证数学规律和公式,这种方法称之为“无字证明”,它比严谨的数学证明更为优雅与有条理.下面是用三块全等的直角三角形移、拼、补所形成的“无字证明”图形.
(1)此图可以用来证明你学过的什么定理?请写出定理的内容;
(2)已知直角三角形直角边长分别为a、b,斜边长为c,图1、图2的面积相等,请你根据此图证明(1)中的定理.
22.如图,已知△ABC中,AB=AC,BD⊥AC于D,BD=3,BC=,求AB的长.
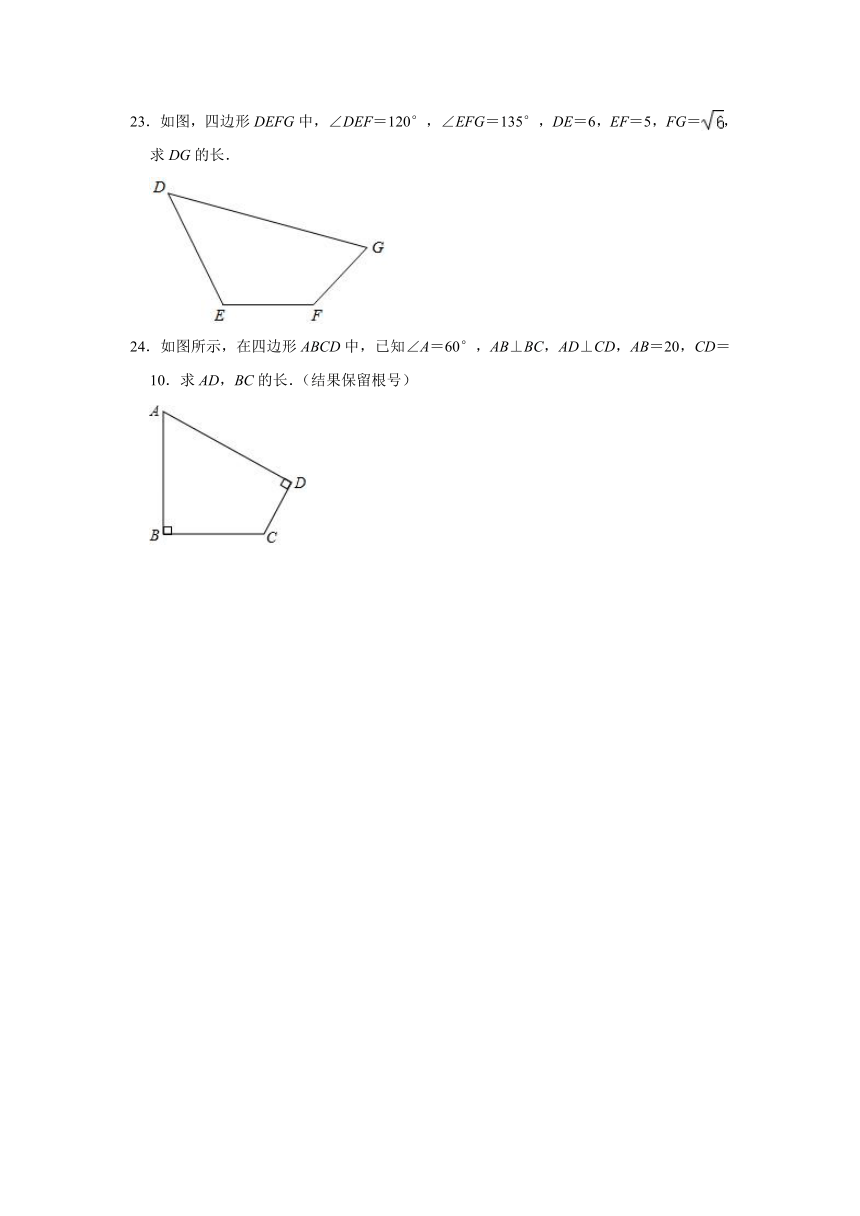
23.如图,四边形DEFG中,∠DEF=120°,∠EFG=135°,DE=6,EF=5,FG=,求DG的长.
24.如图所示,在四边形ABCD中,已知∠A=60°,AB⊥BC,AD⊥CD,AB=20,CD=10.求AD,BC的长.(结果保留根号)
参考答案
1.解:A、∵42+52≠62,不能组成直角三角形,故本选项不符合题意;
B、∵12+()2=22,能组成直角三角形,但不是正整数,故本选项不符合题意;
C、∵62+82=102,能组成直角三角形,故本选项符合题意;
D、∵52+122≠232,不能组成直角三角形,故本选项不符合题意;
故选:C.
2.解:A、∵12+()2≠22,
∴以1,2,为边不能组成三角形,不能组成直角三角形,故本选项不符合题意;
B、∵32+42=52,
∴以5,4,3为边能组成直角三角形,故本选项符合题意;
C、∵42+52≠62,
∴以4,5,6为边不能组成直角三角形,故本选项不符合题意;
D、∵132+142≠152,
∴以13,14,15为边不能组成直角三角形,故本选项不符合题意;
故选:B.
3.解:当∠A:∠B:∠C=3:4:5时,则∠C=180°×=75°,同理可得∠A=45°,∠B=60°,故选项A符合题意;
当∠C=∠A﹣∠B时,可得∠C+∠B=∠A,又∵∠A+∠B+∠C=180°,∴∠C=90°,故选项B不符合题意;
当a2+b2=c2时,则△ABC时直角三角形,故选项C不符合题意;
当a:b:c=6:8:10时,a2+b2=c2,则△ABC时直角三角形,故选项D不符合题意;
故选:A.
4.解:如图,∵∠CBD=90°,CD2=14,BC2=8,
∴BD2=CD2﹣BC2=6,
∴正方形A的面积为6,
故选:A.
5.解:∵入户门的高为2.1米,宽为1.1米,
∴入户门对角线为:≈2.37(米),
故选:C.
6.解:由勾股定理得:另一条直角边为:,
故选:B.
7.解:沿过A的圆柱的高剪开,得出矩形EFGH,
过C作CQ⊥EF于Q,作A关于EH的对称点A′,连接A′C交EH于P,连接AP,则
AP+PC就是蚂蚁到达蜂蜜的最短距离,
∵AE=A′E,A′P=AP,
∴AP+PC=A′P+PC=A′C,
∵CQ=×18cm=9cm,A′Q=12cm﹣4cm+4cm=12cm,
在Rt△A′QC中,由勾股定理得:A′C==15cm,
故选:B.
8.解:如图,过点D作DE⊥AB于点E,
∵AB=2.5米,BE=CD=1.6米,ED=BC=1.2米,
∴AE=AB﹣BE=2.5﹣1.6=0.9(米).
在Rt△ADE中,由勾股定理得到:AD===1.5(米)
故选:B.
9.解:设这个直角三角形的两直角边分别为a,b,
由题意可得,,
∴2ab=(a+b)2﹣(a2+b2)=(m﹣n)2﹣n2=m2﹣2mn,
∴这个直角三角形的面积=ab=.
故选:A.
10.解:如图所示:设直角三角形的斜边为c,
则S1=c2=a2+b2
S2=(a﹣b)2=a2+b2﹣2ab,
∴2ab=S1﹣S2,
∴(a+b)2=a2+2ab+b2=S1+S1﹣S2=2S1﹣S2,
故选:C.
11.解:∵AD是中线,AB=13,BC=10,
∴BD=BC=5.
∵52+122=132,即BD2+AD2=AB2,
∴△ABD是直角三角形,则AD⊥BC,
又∵BD=CD,
∴AC=AB=13,
∴△ABC的周长=13+13+10=36,
故答案为:36.
12.解:由图可知:AD=CD=,AC=,
∴∠ADC=90°,
∴∠ACD=45°,
∴∠BAC+∠BCA=∠ACD=45°,
故答案为:45.
13.解:如图1所示:
过点A作AD⊥BC于点D,
由题意可得:∠B=∠C=60°,
则△ABC是等边三角形,
故BC=AB=AC=2m,
则AD=2sin60°=m,
如图2所示:
过点A作AE⊥BC于点E,
由题意可得:∠B=∠C=60°,
则△ABC是等腰直角三角形,AC=AB,
则AE=BC=m,
故梯子顶端离地面的高度AD下降了(﹣)m.
故答案为:(﹣).
14.解:由题意可知:中间小正方形的边长为a﹣b,
∵每一个直角三角形的面积为:ab=×4=2,
∴4×ab+(a﹣b)2=16,
∴(a﹣b)2=16﹣8=8,
∴a﹣b=2.
故答案为:2.
15.解:设斜边长为c,高为h.
由勾股定理可得:c2=32+42,
则c=5,
直角三角形面积S=×3×4=×c×h
可得h=,
故答案为:.
16.解:∵S1=22,S2=14,
∴S3=S1+S2=22+14=36,
∴BC=6,
∵AC=10,
∴AB=8,
故答案为:8.
17.解:设竹子折断处离地面x尺,则斜边为(10﹣x)尺,
根据勾股定理得:x2+32=(10﹣x)2,
解得:x=4.55.
答:原处还有4.55尺高的竹子.
18.解:正确.理由:
∵m表示大于1的整数,
∴a,b,c都是正整数,且c是最大边,
∵(2m)2+(m2﹣1)2=(m2+1)2,
∴a2+b2=c2,
即a、b、c为勾股数.
当m=2时,可得一组勾股数3,4,5.
19.解:(1),,
(2)如图,连接AC,
在Rt△ACG中,AG=5,CG=1,
∴AC=,
由(1)可得AB2+BC2==26=AC2,
∴△ABC是以AC为斜边的直角三角形,
∴∠ABC=90°.
20.证明:∵DE是BC的垂直平分线,
∴BE=CE=13,
∵AC=12,AE=5,
∴CE2=AC2+AE2,
∴△AEC是直角三角形,
∴△ABC是直角三角形.
21.解:(1)勾股定理:
直角三角形的两条直角边长分别为a、b,斜边长为c,那么a2+b2=c2;
(2)图1的面积为:S1=,
图2的面积为S2=,
∵图1、图2的面积相等,
∴=,
∴a2+b2=c2.
22.解:设AB=AC=x,
∵BD⊥AC,
∴∠BDC=90°,
∴CD==1,
∴AD=x﹣1,
在Rt△BDA中,BD2+AD2=AB2,即32+(x﹣1)2=x2,
解得,x=5,即AB=5.
23.解:延长并反向延长EF,作DA⊥AE于A,GB⊥FB于B,作DC∥AB于C,
∵∠DEF=120°,∠EFG=135°,
∴∠DEA=60°,∠GFB=45°,
∵∠A=∠B=∠C=90°,
∴AE=3,AD=3,FB=GB=,
∴CG=BC﹣BG=AD﹣BG=2,AB=CD=AE+EF+BF=8+,
∴DG==.
24.解:延长AD,BC交于点E,
如图,在Rt△ABE中,AB=20,∠A=60°,
∴,AE=2AB=40.
在Rt△CDE中,CD=10,∠E=90°﹣∠A=30°,
∴CE=2CD=20.
∴DE==10,
∴,
∴.
1.下列各组数中,是勾股数的是( )
A.4,5,6 B.1,2, C.6,8,10 D.5,12,23
2.下列各组数中能作为直角三角形三边长的是( )
A.1,,2 B.3,4,5 C.4,5,6 D.13,14,15
3.已知△ABC中,a、b、c分别是∠A、∠B、∠C的对边,下列条件中不能判断△ABC是直角三角形的是( )
A.∠A:∠B:∠C=3:4:5 B.∠C=∠A﹣∠B
C.a2+b2=c2 D.a:b:c=6:8:10
4.以直角三角形的三边为边向外作正方形,其中两个正方形的面积如图所示,则正方形A的面积为( )
A.6 B.36 C.64 D.8
5.小明家需购买一张大圆桌面(不能折叠,不考虑木板厚度),若入户门的高为2.1米,宽为1.1米,则尽可能大的圆桌的直径可以是( )
A.2.45米 B.2.40米 C.2.35米 D.2.30米
6.若直角三角形的斜边长为,一条直角边长为1,则另一条直角边长为( )
A.5 B. C. D.7
7.如图,圆柱形玻璃杯,高为12cm,底面周长为18cm,在杯内离杯底4cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的A处,则蚂蚁到达蜂蜜的最短距离( )cm.
A.14 B.15 C.16 D.17
8.如图,某自动感应门的正上方A处装着一个感应器,离地AB=2.5米,当人体进入感应器的感应范围内时,感应门就会自动打开.一个身高1.6米的学生CD正对门,缓慢走到离门1.2米的地方时(BC=1.2米),感应门自动打开,则人头顶离感应器的距离AD等于( )
A.1.2米 B.1.5米 C.2.0米 D.2.5米
9.传说,古埃及人常用“拉绳”的方法画直角,有一根长为m的绳子,古埃及人用这根绳子拉出了一个斜边长为n的直角三角形,那么这个直角三角形的面积用含m和n的式子可表示为( )
A. B. C. D.
10.如图,四个全等的直角三角形和中间的小正方形可以拼成一个大正方形,若直角三角形的较长直角边长为a,较短直角边长为b,大正方形面积为S1,小正方形面积为S2,则(a+b)2可以表示为( )
A.S1﹣S2 B.S1+S2 C.2S1﹣S2 D.S1+2S2
11.在△ABC中,AB=13,BC=10,BC边上的中线AD=12,则△ABC的周长为 .
12.如图所示的网格是正方形网格,点A、B、C、D均在格点上,则∠CAB+∠CBA= °.
13.如图,“人字梯”放在水平的地面上,AB=AC,当梯子的一边与地面所夹的锐角α为60°时,两梯角之间的距离BC的长为2m.周日亮亮帮助妈妈整理换季衣服,先使α为60°,后又调整α为45°,则梯子顶端A离地面的高度下降了 m.
14.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b.若ab=4,大正方形的面积为16,则小正方形的边长为 .
15.直角三角形两直角边长分别为3和4,则它斜边上的高为 .
16.如图,由两个直角三角形和三个正方形组成的图形.其中两正方形面积分别是S1=22,S2=14,AC=10,则AB= .
17.《九章算术》是我国古代数学的经典著作.书中有一个“折竹抵地”问题:“今有竹高丈,末折抵地,问折者高几何?”意思是:一根竹子,原来高一丈(一丈为十尺),虫伤有病,一阵风将竹子折断,其竹梢恰好抵地,抵地处离原竹子根部三尺远,问:原处还有多高的竹子?
18.古希腊的哲学家柏拉图曾指出,如果m表示大于1的整数,a=2m,b=m2﹣1,c=m2+1,那么a,b,c为勾股数.你认为对吗?如果对,你能利用这个结论得出一些勾股数吗?
19.如图,小方格都是边长为1的正方形.
(1)求四边形ABCD的边AB与BC的长;
(2)用勾股定理逆定理的知识证明:∠ABC=90°.
20.如图,在△ABC中,DE是BC的垂直平分线,其中AC=12,AE=5,BE=13,证明:△ABC是直角三角形.
21.我们根据图形的移、拼、补可以简单直观地推理验证数学规律和公式,这种方法称之为“无字证明”,它比严谨的数学证明更为优雅与有条理.下面是用三块全等的直角三角形移、拼、补所形成的“无字证明”图形.
(1)此图可以用来证明你学过的什么定理?请写出定理的内容;
(2)已知直角三角形直角边长分别为a、b,斜边长为c,图1、图2的面积相等,请你根据此图证明(1)中的定理.
22.如图,已知△ABC中,AB=AC,BD⊥AC于D,BD=3,BC=,求AB的长.
23.如图,四边形DEFG中,∠DEF=120°,∠EFG=135°,DE=6,EF=5,FG=,求DG的长.
24.如图所示,在四边形ABCD中,已知∠A=60°,AB⊥BC,AD⊥CD,AB=20,CD=10.求AD,BC的长.(结果保留根号)
参考答案
1.解:A、∵42+52≠62,不能组成直角三角形,故本选项不符合题意;
B、∵12+()2=22,能组成直角三角形,但不是正整数,故本选项不符合题意;
C、∵62+82=102,能组成直角三角形,故本选项符合题意;
D、∵52+122≠232,不能组成直角三角形,故本选项不符合题意;
故选:C.
2.解:A、∵12+()2≠22,
∴以1,2,为边不能组成三角形,不能组成直角三角形,故本选项不符合题意;
B、∵32+42=52,
∴以5,4,3为边能组成直角三角形,故本选项符合题意;
C、∵42+52≠62,
∴以4,5,6为边不能组成直角三角形,故本选项不符合题意;
D、∵132+142≠152,
∴以13,14,15为边不能组成直角三角形,故本选项不符合题意;
故选:B.
3.解:当∠A:∠B:∠C=3:4:5时,则∠C=180°×=75°,同理可得∠A=45°,∠B=60°,故选项A符合题意;
当∠C=∠A﹣∠B时,可得∠C+∠B=∠A,又∵∠A+∠B+∠C=180°,∴∠C=90°,故选项B不符合题意;
当a2+b2=c2时,则△ABC时直角三角形,故选项C不符合题意;
当a:b:c=6:8:10时,a2+b2=c2,则△ABC时直角三角形,故选项D不符合题意;
故选:A.
4.解:如图,∵∠CBD=90°,CD2=14,BC2=8,
∴BD2=CD2﹣BC2=6,
∴正方形A的面积为6,
故选:A.
5.解:∵入户门的高为2.1米,宽为1.1米,
∴入户门对角线为:≈2.37(米),
故选:C.
6.解:由勾股定理得:另一条直角边为:,
故选:B.
7.解:沿过A的圆柱的高剪开,得出矩形EFGH,
过C作CQ⊥EF于Q,作A关于EH的对称点A′,连接A′C交EH于P,连接AP,则
AP+PC就是蚂蚁到达蜂蜜的最短距离,
∵AE=A′E,A′P=AP,
∴AP+PC=A′P+PC=A′C,
∵CQ=×18cm=9cm,A′Q=12cm﹣4cm+4cm=12cm,
在Rt△A′QC中,由勾股定理得:A′C==15cm,
故选:B.
8.解:如图,过点D作DE⊥AB于点E,
∵AB=2.5米,BE=CD=1.6米,ED=BC=1.2米,
∴AE=AB﹣BE=2.5﹣1.6=0.9(米).
在Rt△ADE中,由勾股定理得到:AD===1.5(米)
故选:B.
9.解:设这个直角三角形的两直角边分别为a,b,
由题意可得,,
∴2ab=(a+b)2﹣(a2+b2)=(m﹣n)2﹣n2=m2﹣2mn,
∴这个直角三角形的面积=ab=.
故选:A.
10.解:如图所示:设直角三角形的斜边为c,
则S1=c2=a2+b2
S2=(a﹣b)2=a2+b2﹣2ab,
∴2ab=S1﹣S2,
∴(a+b)2=a2+2ab+b2=S1+S1﹣S2=2S1﹣S2,
故选:C.
11.解:∵AD是中线,AB=13,BC=10,
∴BD=BC=5.
∵52+122=132,即BD2+AD2=AB2,
∴△ABD是直角三角形,则AD⊥BC,
又∵BD=CD,
∴AC=AB=13,
∴△ABC的周长=13+13+10=36,
故答案为:36.
12.解:由图可知:AD=CD=,AC=,
∴∠ADC=90°,
∴∠ACD=45°,
∴∠BAC+∠BCA=∠ACD=45°,
故答案为:45.
13.解:如图1所示:
过点A作AD⊥BC于点D,
由题意可得:∠B=∠C=60°,
则△ABC是等边三角形,
故BC=AB=AC=2m,
则AD=2sin60°=m,
如图2所示:
过点A作AE⊥BC于点E,
由题意可得:∠B=∠C=60°,
则△ABC是等腰直角三角形,AC=AB,
则AE=BC=m,
故梯子顶端离地面的高度AD下降了(﹣)m.
故答案为:(﹣).
14.解:由题意可知:中间小正方形的边长为a﹣b,
∵每一个直角三角形的面积为:ab=×4=2,
∴4×ab+(a﹣b)2=16,
∴(a﹣b)2=16﹣8=8,
∴a﹣b=2.
故答案为:2.
15.解:设斜边长为c,高为h.
由勾股定理可得:c2=32+42,
则c=5,
直角三角形面积S=×3×4=×c×h
可得h=,
故答案为:.
16.解:∵S1=22,S2=14,
∴S3=S1+S2=22+14=36,
∴BC=6,
∵AC=10,
∴AB=8,
故答案为:8.
17.解:设竹子折断处离地面x尺,则斜边为(10﹣x)尺,
根据勾股定理得:x2+32=(10﹣x)2,
解得:x=4.55.
答:原处还有4.55尺高的竹子.
18.解:正确.理由:
∵m表示大于1的整数,
∴a,b,c都是正整数,且c是最大边,
∵(2m)2+(m2﹣1)2=(m2+1)2,
∴a2+b2=c2,
即a、b、c为勾股数.
当m=2时,可得一组勾股数3,4,5.
19.解:(1),,
(2)如图,连接AC,
在Rt△ACG中,AG=5,CG=1,
∴AC=,
由(1)可得AB2+BC2==26=AC2,
∴△ABC是以AC为斜边的直角三角形,
∴∠ABC=90°.
20.证明:∵DE是BC的垂直平分线,
∴BE=CE=13,
∵AC=12,AE=5,
∴CE2=AC2+AE2,
∴△AEC是直角三角形,
∴△ABC是直角三角形.
21.解:(1)勾股定理:
直角三角形的两条直角边长分别为a、b,斜边长为c,那么a2+b2=c2;
(2)图1的面积为:S1=,
图2的面积为S2=,
∵图1、图2的面积相等,
∴=,
∴a2+b2=c2.
22.解:设AB=AC=x,
∵BD⊥AC,
∴∠BDC=90°,
∴CD==1,
∴AD=x﹣1,
在Rt△BDA中,BD2+AD2=AB2,即32+(x﹣1)2=x2,
解得,x=5,即AB=5.
23.解:延长并反向延长EF,作DA⊥AE于A,GB⊥FB于B,作DC∥AB于C,
∵∠DEF=120°,∠EFG=135°,
∴∠DEA=60°,∠GFB=45°,
∵∠A=∠B=∠C=90°,
∴AE=3,AD=3,FB=GB=,
∴CG=BC﹣BG=AD﹣BG=2,AB=CD=AE+EF+BF=8+,
∴DG==.
24.解:延长AD,BC交于点E,
如图,在Rt△ABE中,AB=20,∠A=60°,
∴,AE=2AB=40.
在Rt△CDE中,CD=10,∠E=90°﹣∠A=30°,
∴CE=2CD=20.
∴DE==10,
∴,
∴.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
