12.1全等三角形 同步练习 2023—2024学年人教版数学八年级上册(含答案)
文档属性
| 名称 | 12.1全等三角形 同步练习 2023—2024学年人教版数学八年级上册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 145.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-05 17:28:39 | ||
图片预览

文档简介
12.1全等三角形
一、选择题
1.下列图形是全等图形的是( )
A. B.
C. D.
2.下列说法错误的是( )
A.如果两个图形全等,那么它们的形状和大小一定相同;
B.图形全等,只与形状,大小有关,而与它们的位置无关;
C.全等图形的面积相等,面积相等的两个图形是全等图形;
D.全等三角形的对应边相等,对应角相等.
3.如图,某人不小心将一块正五边形玻璃打碎成四块,若想到玻璃店配一块与原来一样大小的五边形玻璃,那么最省事的方法应该带玻璃碎片( )
A.① B.①② C.①③ D.①③④
4.已知且的面积为则边上的高等于( )
A.13 B.3 C.4 D.6
5.如图,△ABC≌△A'B'C',则∠C的度数是( )
A.107° B.73° C.56° D.51°
6.如图,△ACE≌△DBF,若AD=11cm,BC=5cm,则AB长为( )
A.6cm B.7cm C.4cm D.3cm
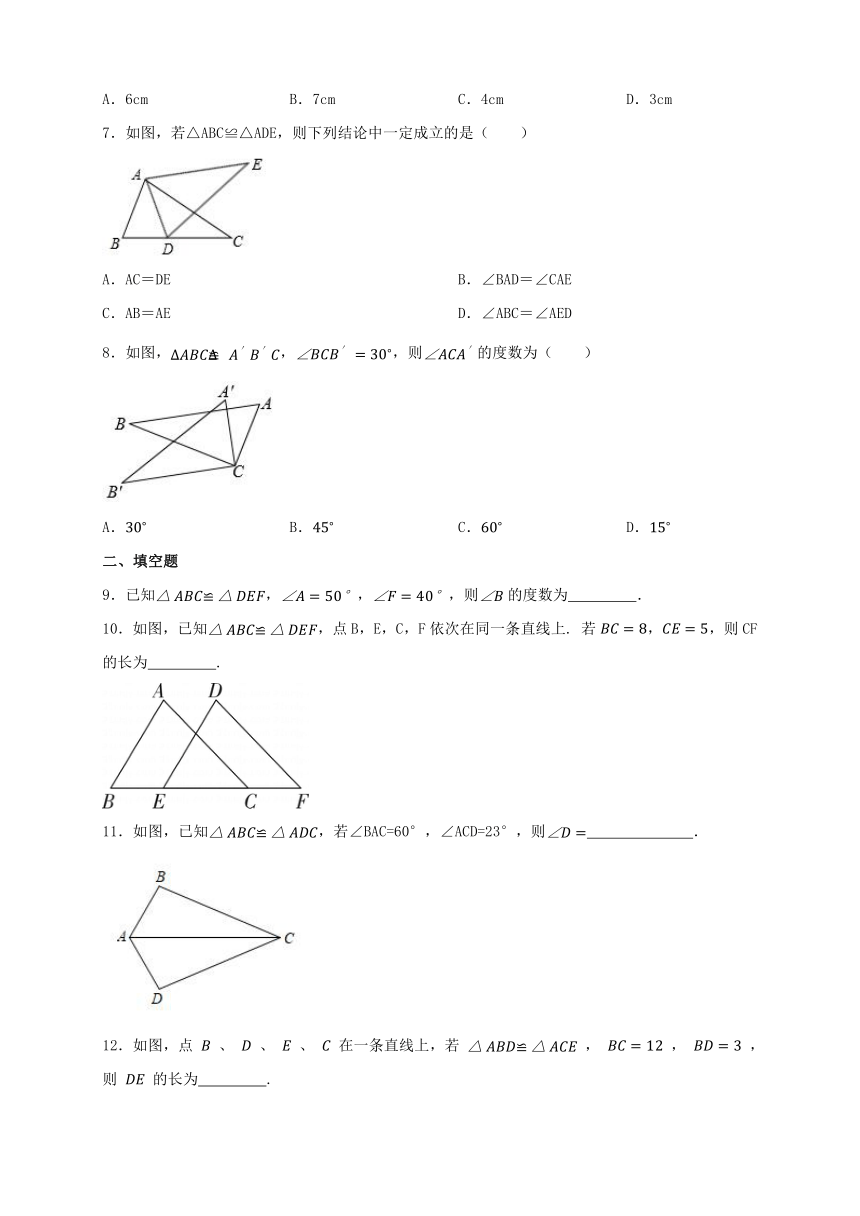
7.如图,若△ABC≌△ADE,则下列结论中一定成立的是( )
A.AC=DE B.∠BAD=∠CAE
C.AB=AE D.∠ABC=∠AED
8.如图,,,则的度数为( )
A. B. C. D.
二、填空题
9.已知,,,则的度数为 .
10.如图,已知,点B,E,C,F依次在同一条直线上. 若,,则CF的长为 .
11.如图,已知,若∠BAC=60°,∠ACD=23°,则 .
12.如图,点 、 、 、 在一条直线上,若 , , ,则 的长为 .
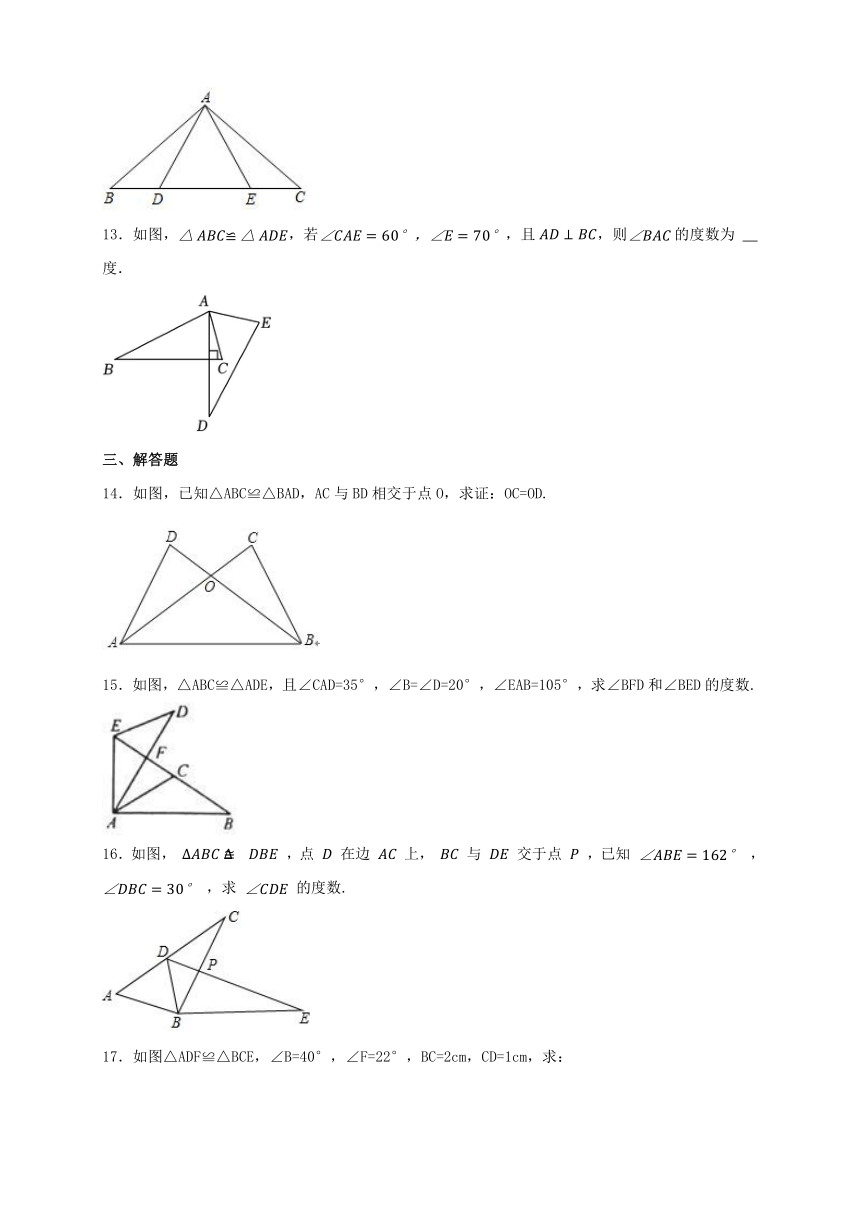
13.如图,,若,且,则的度数为 度.
三、解答题
14.如图,已知△ABC≌△BAD,AC与BD相交于点O,求证:OC=OD.
15.如图,△ABC≌△ADE,且∠CAD=35°,∠B=∠D=20°,∠EAB=105°,求∠BFD和∠BED的度数.
16.如图, ,点 在边 上, 与 交于点 ,已知 , ,求 的度数.
17.如图△ADF≌△BCE,∠B=40°,∠F=22°,BC=2cm,CD=1cm,求:
(1)∠1的度数;
(2)AC的长.
18.如图所示,已知△ABD≌△CFD,AD⊥BC于D.
(1)求证∶ CE⊥AB
(2)已知BC=7,AD=5,求 AF的长.
参考答案
1.B
2.C
3.A
4.D
5.B
6.D
7.B
8.A
9.
10.3
11.97°/97度
12.6
13.80
14.证明:∵△ABC≌△BAD,
∴∠CAB=∠DBA,AC=BD,
∴OA=OB,
∴AC﹣OA=BD﹣OB,
即:OC=OD.
15.解:∵△ABC≌△ADE,
∴ ∠EAD=∠CAB,
又∵∠CAD=35°,∠EAB=105°
∴∠EAD+∠DAC+∠CAB=∠EAB=105°,
∴∠EAD=∠DAC=∠CAB=35°,
∴∠DFB=∠DAB+∠B=35°+35°+20°=90°,
∴∠BED=∠BFD-∠D=90°-20°=70°.
16.解:∵∠ABE=162°,∠DBC=30°,
∴∠ABD+∠CBE=132°,
∵△ABC≌△DBE,
∴∠ABC=∠DBE.
∴∠ABD=∠CBE=132°÷2=66°.
又由△ABC≌△DBE,
∴AB=BD,∠A=∠BDE,
∴∠ADB=∠A=∠BDE=(180°-∠ABD)÷2=57°.
∴∠CDE=180°-∠ADB-∠BDE=66°.
17.(1)解:∵△ADF≌△BCE,
∴∠F=∠E=22°,
∵∠1是△BCE的一个外角,
∴∠1=∠B+∠E=40°+22°=62°
(2)∵△ADF≌△BCE,
∴AD=BC=2cm,
∴AC=AD+DC=2+1=3cm
18.(1)证明:∵AD⊥BC
∴∠CDF=90°
∵△ABD≌△CFD,
∴∠BAD=∠DCF,
又∵∠AFE=∠CFD,
∴∠AEF=∠CDF=90°,
∴CE⊥AB;
(2)解:∵△ABD≌△CFD,
∴BD=DF,AD=DC,
∵BC=7,AD=5,
∴BD=BC CD=2,
∴AF=AD DF=5 2=3.
一、选择题
1.下列图形是全等图形的是( )
A. B.
C. D.
2.下列说法错误的是( )
A.如果两个图形全等,那么它们的形状和大小一定相同;
B.图形全等,只与形状,大小有关,而与它们的位置无关;
C.全等图形的面积相等,面积相等的两个图形是全等图形;
D.全等三角形的对应边相等,对应角相等.
3.如图,某人不小心将一块正五边形玻璃打碎成四块,若想到玻璃店配一块与原来一样大小的五边形玻璃,那么最省事的方法应该带玻璃碎片( )
A.① B.①② C.①③ D.①③④
4.已知且的面积为则边上的高等于( )
A.13 B.3 C.4 D.6
5.如图,△ABC≌△A'B'C',则∠C的度数是( )
A.107° B.73° C.56° D.51°
6.如图,△ACE≌△DBF,若AD=11cm,BC=5cm,则AB长为( )
A.6cm B.7cm C.4cm D.3cm
7.如图,若△ABC≌△ADE,则下列结论中一定成立的是( )
A.AC=DE B.∠BAD=∠CAE
C.AB=AE D.∠ABC=∠AED
8.如图,,,则的度数为( )
A. B. C. D.
二、填空题
9.已知,,,则的度数为 .
10.如图,已知,点B,E,C,F依次在同一条直线上. 若,,则CF的长为 .
11.如图,已知,若∠BAC=60°,∠ACD=23°,则 .
12.如图,点 、 、 、 在一条直线上,若 , , ,则 的长为 .
13.如图,,若,且,则的度数为 度.
三、解答题
14.如图,已知△ABC≌△BAD,AC与BD相交于点O,求证:OC=OD.
15.如图,△ABC≌△ADE,且∠CAD=35°,∠B=∠D=20°,∠EAB=105°,求∠BFD和∠BED的度数.
16.如图, ,点 在边 上, 与 交于点 ,已知 , ,求 的度数.
17.如图△ADF≌△BCE,∠B=40°,∠F=22°,BC=2cm,CD=1cm,求:
(1)∠1的度数;
(2)AC的长.
18.如图所示,已知△ABD≌△CFD,AD⊥BC于D.
(1)求证∶ CE⊥AB
(2)已知BC=7,AD=5,求 AF的长.
参考答案
1.B
2.C
3.A
4.D
5.B
6.D
7.B
8.A
9.
10.3
11.97°/97度
12.6
13.80
14.证明:∵△ABC≌△BAD,
∴∠CAB=∠DBA,AC=BD,
∴OA=OB,
∴AC﹣OA=BD﹣OB,
即:OC=OD.
15.解:∵△ABC≌△ADE,
∴ ∠EAD=∠CAB,
又∵∠CAD=35°,∠EAB=105°
∴∠EAD+∠DAC+∠CAB=∠EAB=105°,
∴∠EAD=∠DAC=∠CAB=35°,
∴∠DFB=∠DAB+∠B=35°+35°+20°=90°,
∴∠BED=∠BFD-∠D=90°-20°=70°.
16.解:∵∠ABE=162°,∠DBC=30°,
∴∠ABD+∠CBE=132°,
∵△ABC≌△DBE,
∴∠ABC=∠DBE.
∴∠ABD=∠CBE=132°÷2=66°.
又由△ABC≌△DBE,
∴AB=BD,∠A=∠BDE,
∴∠ADB=∠A=∠BDE=(180°-∠ABD)÷2=57°.
∴∠CDE=180°-∠ADB-∠BDE=66°.
17.(1)解:∵△ADF≌△BCE,
∴∠F=∠E=22°,
∵∠1是△BCE的一个外角,
∴∠1=∠B+∠E=40°+22°=62°
(2)∵△ADF≌△BCE,
∴AD=BC=2cm,
∴AC=AD+DC=2+1=3cm
18.(1)证明:∵AD⊥BC
∴∠CDF=90°
∵△ABD≌△CFD,
∴∠BAD=∠DCF,
又∵∠AFE=∠CFD,
∴∠AEF=∠CDF=90°,
∴CE⊥AB;
(2)解:∵△ABD≌△CFD,
∴BD=DF,AD=DC,
∵BC=7,AD=5,
∴BD=BC CD=2,
∴AF=AD DF=5 2=3.
