13.1轴对称 同步练习 2023—2024学年人教版数学八年级上册(含答案)
文档属性
| 名称 | 13.1轴对称 同步练习 2023—2024学年人教版数学八年级上册(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 202.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-05 17:31:49 | ||
图片预览

文档简介
13.1轴对称
一、选择题
1.在一些汉字的美术字中,有一些是轴对称图形,下面四个美术字中,可以近似地看作是轴对称图形的是( )
A. B. C. D.
2.如图,是一个经过改造的台球桌面的示意图,图中四个角上的阴影部分分别表示四个入球孔,如果一个球按图中所示的方向被击出,该球最后落入1号袋,经过反射的次数是( )
A.4次 B.5次 C.6次 D.7次
3.如图,若与关于直线对称,交于点,则下列说法中,不一定正确的是( )
A. B. C. D.
4.如图,∠AOB内一点P,P1,P2分别是P关于OA、OB的对称点,P1P2交OA于点M,交OB于点N.若△PMN的周长是5cm,则P1P2的长为( )
A.6cm B.5cm C.4cm D.3cm
5.如图,在中,直线为的垂直平分线,并交于点D,连接.若,,则的长为( )
A. B. C. D.
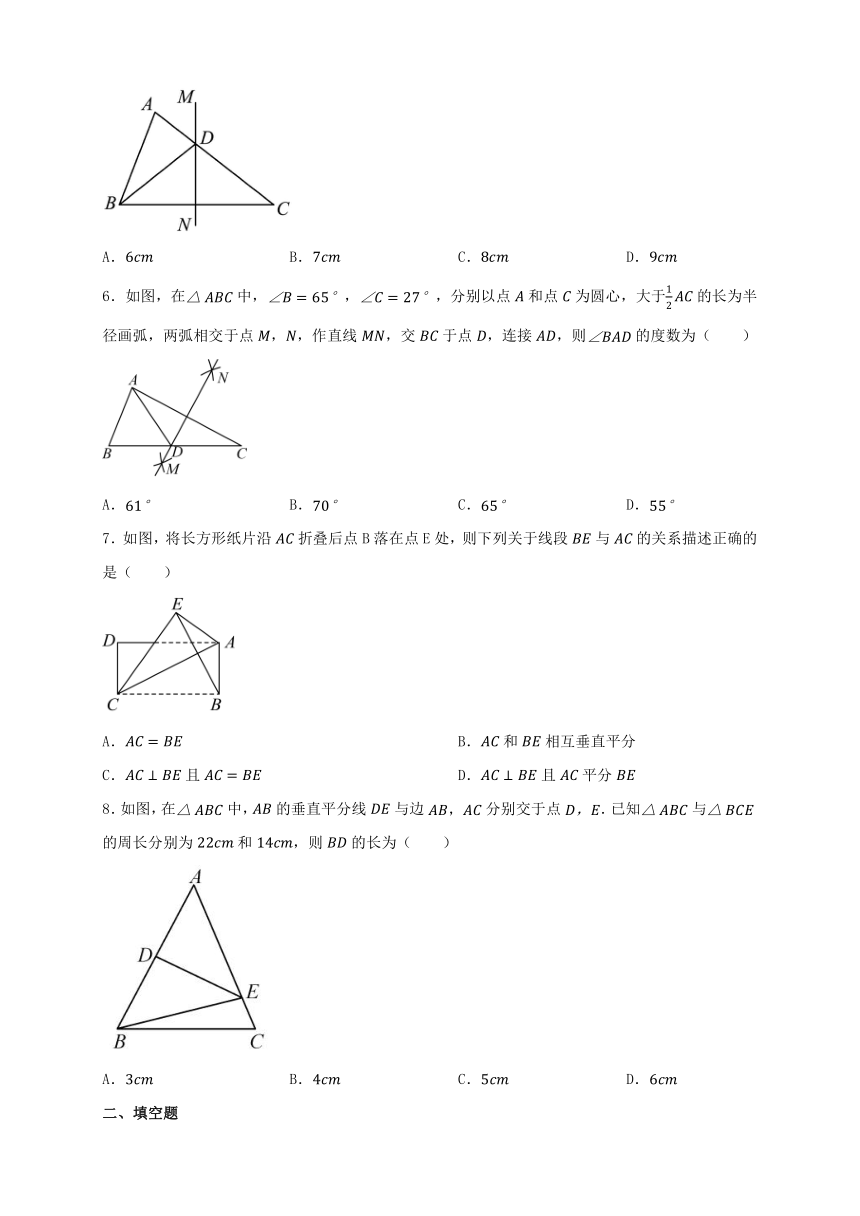
6.如图,在中,,,分别以点和点为圆心,大于的长为半径画弧,两弧相交于点,,作直线,交于点,连接,则的度数为( )
A. B. C. D.
7.如图,将长方形纸片沿折叠后点B落在点E处,则下列关于线段与的关系描述正确的是( )
A. B.和相互垂直平分
C.且 D.且平分
8.如图,在中,的垂直平分线与边分别交于点.已知与的周长分别为和,则的长为( )
A. B. C. D.
二、填空题
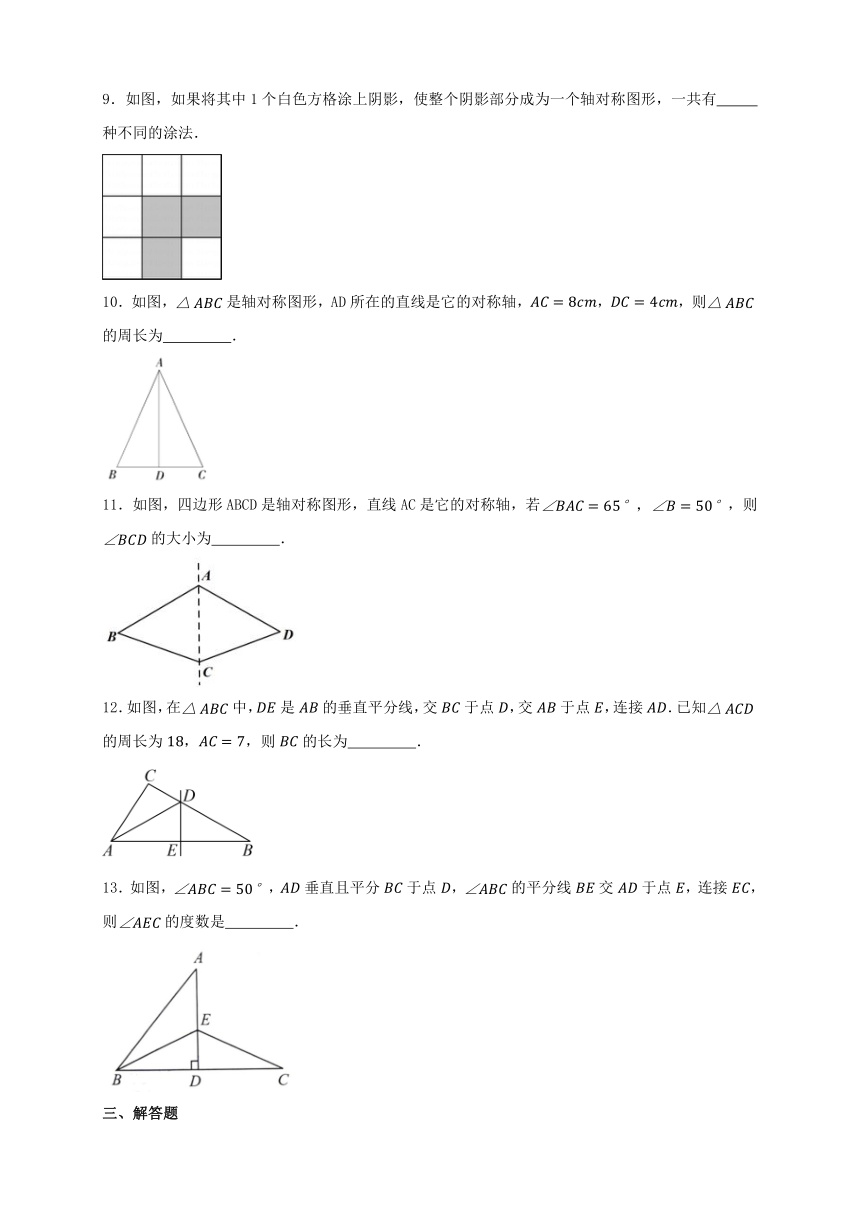
9.如图,如果将其中1个白色方格涂上阴影,使整个阴影部分成为一个轴对称图形,一共有 种不同的涂法.
10.如图,是轴对称图形,AD所在的直线是它的对称轴,,,则的周长为 .
11.如图,四边形ABCD是轴对称图形,直线AC是它的对称轴,若,则的大小为 .
12.如图,在中,是的垂直平分线,交于点,交于点,连接.已知的周长为,,则的长为 .
13.如图,,垂直且平分于点,的平分线交于点,连接,则的度数是 .
三、解答题
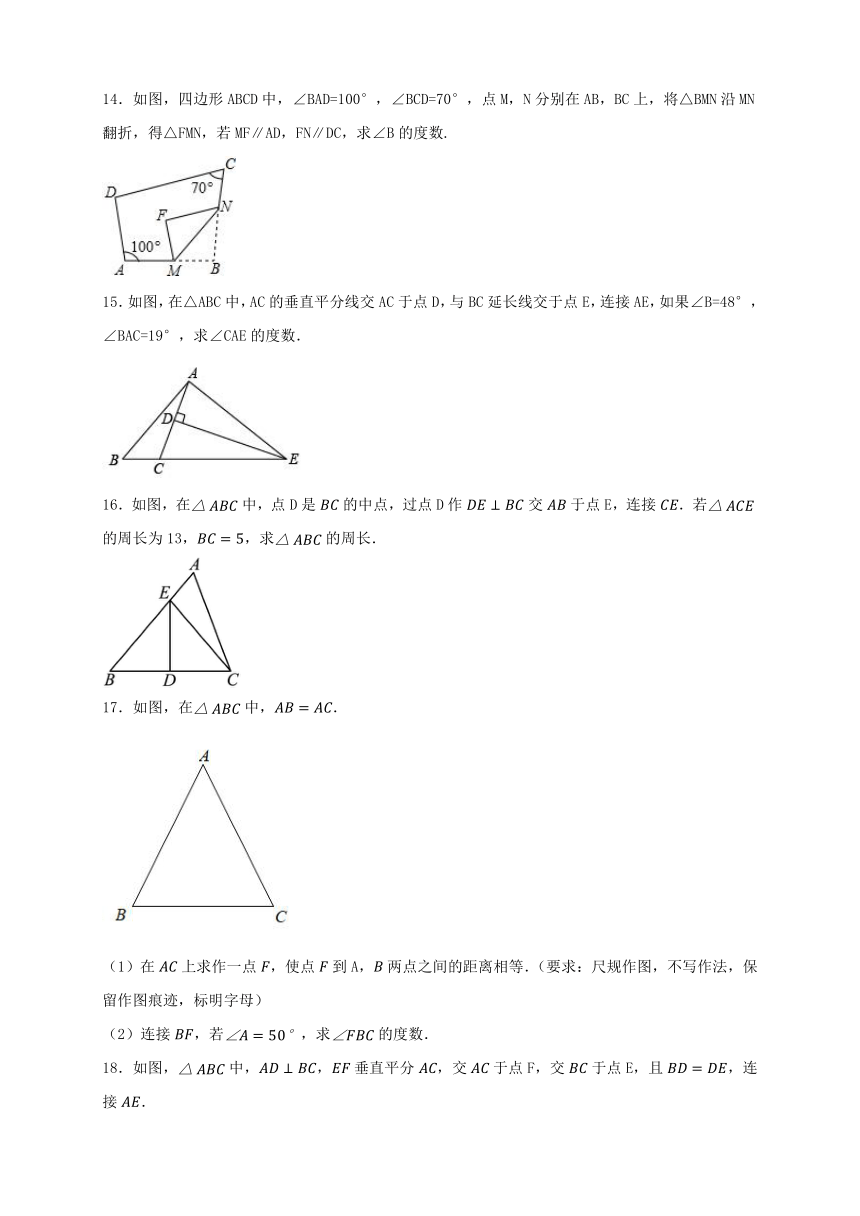
14.如图,四边形ABCD中,∠BAD=100°,∠BCD=70°,点M,N分别在AB,BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,求∠B的度数.
15.如图,在△ABC中,AC的垂直平分线交AC于点D,与BC延长线交于点E,连接AE,如果∠B=48°,∠BAC=19°,求∠CAE的度数.
16.如图,在中,点D是的中点,过点D作交于点E,连接.若的周长为13,,求的周长.
17.如图,在中,.
(1)在上求作一点,使点到A,两点之间的距离相等.(要求:尺规作图,不写作法,保留作图痕迹,标明字母)
(2)连接,若,求的度数.
18.如图,中,,垂直平分,交于点F,交于点E,且,连接.
(1)若,求的度数;
(2)若的周长为,,求的长.
参考答案
1.C
2.C
3.B
4.B
5.A
6.A
7.D
8.B
9.4
10.24cm
11.130°
12.11
13.
14.解:∵MF∥AD,FN∥DC,
∴∠BMF=∠A=100°,∠BNF=∠C=70°,
∵△BMN沿MN翻折得△FMN,
∴∠BMN= ∠BMF= ×100°=50°,
∠BNM= ∠BNF= ×70°=35°,
在△BMN中,∠B=180°-(∠BMN+∠BNM)=180°-(50°+35°)=180°-85°=95°
15.解:∵
∴
又∵ED垂直平分AC
∴
∴
∴的度数为.
16.解:∵点D是的中点,,
∴是线段的中垂线,
∴,
∵的周长为13,
∴,
∴的周长.
17.(1)解:所作的点F如图所示:
(2)解:由(1)作图可知:垂直平分,
∴,
∵,
∴,
∴.
18.(1)证明:∵,点E在上,
∴,
又∵,
∴在线段的垂直平分线上,
∴,
∴,
∵垂直平分,
∴,
∴,
∵
∴ ;
(2)解:
∵的周长,
∴,
∴,
∴,
∵,,
∴,
∴,即.
一、选择题
1.在一些汉字的美术字中,有一些是轴对称图形,下面四个美术字中,可以近似地看作是轴对称图形的是( )
A. B. C. D.
2.如图,是一个经过改造的台球桌面的示意图,图中四个角上的阴影部分分别表示四个入球孔,如果一个球按图中所示的方向被击出,该球最后落入1号袋,经过反射的次数是( )
A.4次 B.5次 C.6次 D.7次
3.如图,若与关于直线对称,交于点,则下列说法中,不一定正确的是( )
A. B. C. D.
4.如图,∠AOB内一点P,P1,P2分别是P关于OA、OB的对称点,P1P2交OA于点M,交OB于点N.若△PMN的周长是5cm,则P1P2的长为( )
A.6cm B.5cm C.4cm D.3cm
5.如图,在中,直线为的垂直平分线,并交于点D,连接.若,,则的长为( )
A. B. C. D.
6.如图,在中,,,分别以点和点为圆心,大于的长为半径画弧,两弧相交于点,,作直线,交于点,连接,则的度数为( )
A. B. C. D.
7.如图,将长方形纸片沿折叠后点B落在点E处,则下列关于线段与的关系描述正确的是( )
A. B.和相互垂直平分
C.且 D.且平分
8.如图,在中,的垂直平分线与边分别交于点.已知与的周长分别为和,则的长为( )
A. B. C. D.
二、填空题
9.如图,如果将其中1个白色方格涂上阴影,使整个阴影部分成为一个轴对称图形,一共有 种不同的涂法.
10.如图,是轴对称图形,AD所在的直线是它的对称轴,,,则的周长为 .
11.如图,四边形ABCD是轴对称图形,直线AC是它的对称轴,若,则的大小为 .
12.如图,在中,是的垂直平分线,交于点,交于点,连接.已知的周长为,,则的长为 .
13.如图,,垂直且平分于点,的平分线交于点,连接,则的度数是 .
三、解答题
14.如图,四边形ABCD中,∠BAD=100°,∠BCD=70°,点M,N分别在AB,BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,求∠B的度数.
15.如图,在△ABC中,AC的垂直平分线交AC于点D,与BC延长线交于点E,连接AE,如果∠B=48°,∠BAC=19°,求∠CAE的度数.
16.如图,在中,点D是的中点,过点D作交于点E,连接.若的周长为13,,求的周长.
17.如图,在中,.
(1)在上求作一点,使点到A,两点之间的距离相等.(要求:尺规作图,不写作法,保留作图痕迹,标明字母)
(2)连接,若,求的度数.
18.如图,中,,垂直平分,交于点F,交于点E,且,连接.
(1)若,求的度数;
(2)若的周长为,,求的长.
参考答案
1.C
2.C
3.B
4.B
5.A
6.A
7.D
8.B
9.4
10.24cm
11.130°
12.11
13.
14.解:∵MF∥AD,FN∥DC,
∴∠BMF=∠A=100°,∠BNF=∠C=70°,
∵△BMN沿MN翻折得△FMN,
∴∠BMN= ∠BMF= ×100°=50°,
∠BNM= ∠BNF= ×70°=35°,
在△BMN中,∠B=180°-(∠BMN+∠BNM)=180°-(50°+35°)=180°-85°=95°
15.解:∵
∴
又∵ED垂直平分AC
∴
∴
∴的度数为.
16.解:∵点D是的中点,,
∴是线段的中垂线,
∴,
∵的周长为13,
∴,
∴的周长.
17.(1)解:所作的点F如图所示:
(2)解:由(1)作图可知:垂直平分,
∴,
∵,
∴,
∴.
18.(1)证明:∵,点E在上,
∴,
又∵,
∴在线段的垂直平分线上,
∴,
∴,
∵垂直平分,
∴,
∴,
∵
∴ ;
(2)解:
∵的周长,
∴,
∴,
∴,
∵,,
∴,
∴,即.
