13.3等腰三角形 同步练习 2023—2024学年人教版数学八年级上册(含答案)
文档属性
| 名称 | 13.3等腰三角形 同步练习 2023—2024学年人教版数学八年级上册(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 256.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-05 17:49:56 | ||
图片预览


文档简介
13.3等腰三角形
一、选择题
1.等腰三角形的两条边长分别为5和6,则这个等腰三角形的周长是( )
A.或 B. C. D.或
2.若等腰三角形有一个内角为,则这个等腰三角形的底角是( )
A. B. C. D.
3.在中,和的度数如下,能判定是等腰三角形的是( )
A., B.,
C., D.,
4.为等边三角形,点 D在线段上,且,则的度数是( )
A. B. C. D.
5.由于木质衣架没有柔性,在挂置衣服的时候不太方便操作.小颖同学设计一种衣架,在使用时能轻易收拢,然后秦进衣服后松开即可.如图①,衣架杆(为衣架的固定点);如图②,若衣架收拢时,,则此时,两点之间的距离是( )
A. B. C. D.
6.如图,在中,,,,则边的长度是( )
A.3 B.4 C. D.
7.如图,在中,,点,于点,于点,,则( )
A. B. C. D.
8.如图,和都是等边三角形,点D,E,F分别在边上,若的周长为15,,则的长为( )
A.2 B.3 C.4 D.5
二、填空题
9.已知一等腰三角形的两边长分别为和,则此三角形的周长为 .
10.在中,,,点P是上一动点,当为等腰三角形时,的度数为 .
11.如图,在中,,D,E是内的两点,平分,,若,,则的长是 .
12.如图,在△ABC中,AB=AC,∠B=60°,AD平分∠BAC,点E是线段BC延长线上一点,连接AE,点C在AE的垂直平分线上,若CE=8cm,则AB+BD= cm.
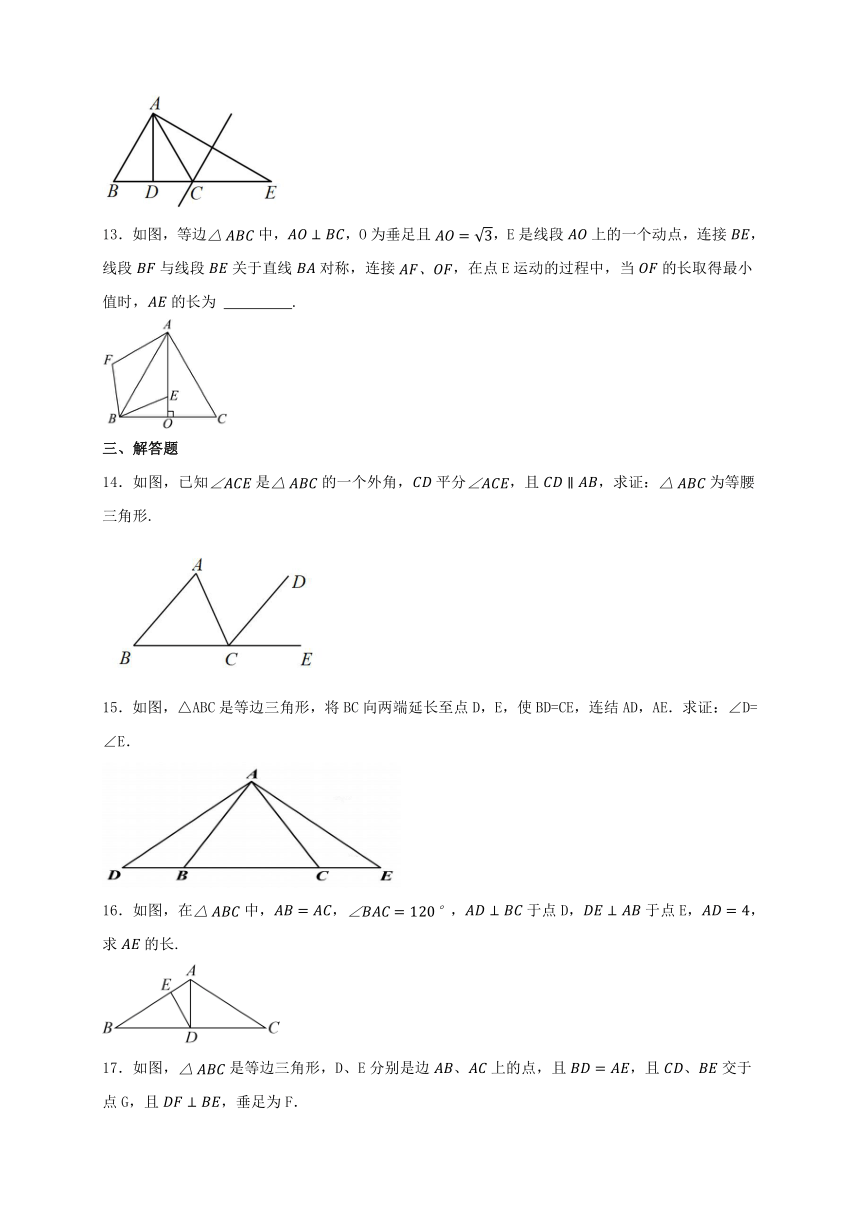
13.如图,等边中,,O为垂足且,E是线段上的一个动点,连接,线段与线段关于直线对称,连接,在点E运动的过程中,当的长取得最小值时,的长为 .
三、解答题
14.如图,已知是的一个外角,平分,且,求证:为等腰三角形.
15.如图,△ABC是等边三角形,将BC向两端延长至点D,E,使BD=CE,连结AD,AE.求证:∠D=∠E.
16.如图,在中,,,于点D,于点E,,求的长.
17.如图,是等边三角形,D、E分别是边、上的点,且,且、交于点G,且,垂足为F.
(1)求证:;
(2)若,求DG的长度.
18.如图,点是等边内一点,点是外的一点,,连接.
(1)求证:是等边三角形;
(2)若,,,求的长.
参考答案
1.D
2.C
3.C
4.C
5.C
6.B
7.D
8.B
9.5
10.
11.16
12.12
13.
14.证明:平分,
,
,
,,
,
,
为等腰三角形.
15.证明:∵△ABC是等边三角形,
∴AB=AC,∠ABC=∠ACB= 60°,
∴∠ABD=∠ACE= 120°,
在△ABD与△ACE中
∵BD= CE,∠ABD=∠ACE,AB=AC,
∴△ABD≌△ACE (SAS),
∴∠D=∠E
16.解:∵,,,
∴.
∵,
∴,
∴,
∴.
17.(1)证明:∵ 是等边三角形,
∴ , ,
∵
∴
∴
在 与 中, ,
∴ ≌ ,
∴ ;
(2)解:
∵ ,
∴ ,
∴
∵ ,即 ,
∴ ,
∴在 中, ,
∵ ,
∴ .
18.(1)证明:∵,
∴,
∵为等边三角形,
∴,
∴,
即,
∴是等边三角形.
(2)解:∵,,
∴,
∵,
∴,
∵是等边三角形.
∴,,
∴,
,
∴在中,,
∴.
一、选择题
1.等腰三角形的两条边长分别为5和6,则这个等腰三角形的周长是( )
A.或 B. C. D.或
2.若等腰三角形有一个内角为,则这个等腰三角形的底角是( )
A. B. C. D.
3.在中,和的度数如下,能判定是等腰三角形的是( )
A., B.,
C., D.,
4.为等边三角形,点 D在线段上,且,则的度数是( )
A. B. C. D.
5.由于木质衣架没有柔性,在挂置衣服的时候不太方便操作.小颖同学设计一种衣架,在使用时能轻易收拢,然后秦进衣服后松开即可.如图①,衣架杆(为衣架的固定点);如图②,若衣架收拢时,,则此时,两点之间的距离是( )
A. B. C. D.
6.如图,在中,,,,则边的长度是( )
A.3 B.4 C. D.
7.如图,在中,,点,于点,于点,,则( )
A. B. C. D.
8.如图,和都是等边三角形,点D,E,F分别在边上,若的周长为15,,则的长为( )
A.2 B.3 C.4 D.5
二、填空题
9.已知一等腰三角形的两边长分别为和,则此三角形的周长为 .
10.在中,,,点P是上一动点,当为等腰三角形时,的度数为 .
11.如图,在中,,D,E是内的两点,平分,,若,,则的长是 .
12.如图,在△ABC中,AB=AC,∠B=60°,AD平分∠BAC,点E是线段BC延长线上一点,连接AE,点C在AE的垂直平分线上,若CE=8cm,则AB+BD= cm.
13.如图,等边中,,O为垂足且,E是线段上的一个动点,连接,线段与线段关于直线对称,连接,在点E运动的过程中,当的长取得最小值时,的长为 .
三、解答题
14.如图,已知是的一个外角,平分,且,求证:为等腰三角形.
15.如图,△ABC是等边三角形,将BC向两端延长至点D,E,使BD=CE,连结AD,AE.求证:∠D=∠E.
16.如图,在中,,,于点D,于点E,,求的长.
17.如图,是等边三角形,D、E分别是边、上的点,且,且、交于点G,且,垂足为F.
(1)求证:;
(2)若,求DG的长度.
18.如图,点是等边内一点,点是外的一点,,连接.
(1)求证:是等边三角形;
(2)若,,,求的长.
参考答案
1.D
2.C
3.C
4.C
5.C
6.B
7.D
8.B
9.5
10.
11.16
12.12
13.
14.证明:平分,
,
,
,,
,
,
为等腰三角形.
15.证明:∵△ABC是等边三角形,
∴AB=AC,∠ABC=∠ACB= 60°,
∴∠ABD=∠ACE= 120°,
在△ABD与△ACE中
∵BD= CE,∠ABD=∠ACE,AB=AC,
∴△ABD≌△ACE (SAS),
∴∠D=∠E
16.解:∵,,,
∴.
∵,
∴,
∴,
∴.
17.(1)证明:∵ 是等边三角形,
∴ , ,
∵
∴
∴
在 与 中, ,
∴ ≌ ,
∴ ;
(2)解:
∵ ,
∴ ,
∴
∵ ,即 ,
∴ ,
∴在 中, ,
∵ ,
∴ .
18.(1)证明:∵,
∴,
∵为等边三角形,
∴,
∴,
即,
∴是等边三角形.
(2)解:∵,,
∴,
∵,
∴,
∵是等边三角形.
∴,,
∴,
,
∴在中,,
∴.
