数学人教A版(新课标)高中必修第一册 《5.6 函数y=Asin(ωx φ)(第二课时)》优秀教学设计
文档属性
| 名称 | 数学人教A版(新课标)高中必修第一册 《5.6 函数y=Asin(ωx φ)(第二课时)》优秀教学设计 |

|
|
| 格式 | docx | ||
| 文件大小 | 443.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-05 00:00:00 | ||
图片预览


文档简介
《5.6 函数y=Asin(ωx+φ)(第二课时)》
教学设计
(
教学目标
)
1.掌握参数A对函数y=Asin(ωx+φ)图象的影响,理解参数A在圆周运动中的实际意义,掌握这个函数的性质,发展数学抽象、逻辑推理与直观想象的素养.
2.理解从正弦曲线到函数y=Asin(ωx+φ)图象的变换过程,能用五点(作图)法画函数y=Asin(ωx+φ)图象.
3.会运用函数y=Asin(ωx+φ)的图象与性质解决简单的数学问题和实际问题.
(
教学重难点
)
教学重点:参数A对函数y=Asin(ωx+φ)图象的影响,以及从从正弦曲线到函数y=Asin(ωx+φ)图象的变换过程..
教学难点:从正弦曲线经过图象变换得到函数y=Asin(ωx+φ)图象.
(
课前准备
)
Geogebra软件、PPT课件.借助Geogebra软件,通过作动画可以演示参数A,φ,ω对函数y=Asin(ωx+φ)图象的影响.
资源引用:【数学探究】探索A(A>0)对y=Asin(ωx+φ)图象的影响
【数学探究】画函数y=Asin(ωx+φ)的图象
(
教学过程
)
(一)整体感知
引导语:通过上节课的学习,我们从实际问题出发,建立了一个新的函数y=Asin(ωx+φ),并按照函数的研究套路,研究了该函数的图象中的部分问题.现在继续上一节课的研究.
(二)新知探究
6.探索A(A>0)对函数y=Asin(ωx+φ)的图象的影响
问题6:当参数A变化时,对函数y=Asin(ωx+φ)图象有什么影响?类比ω与φ的研究方法,你计划怎样进行研究?
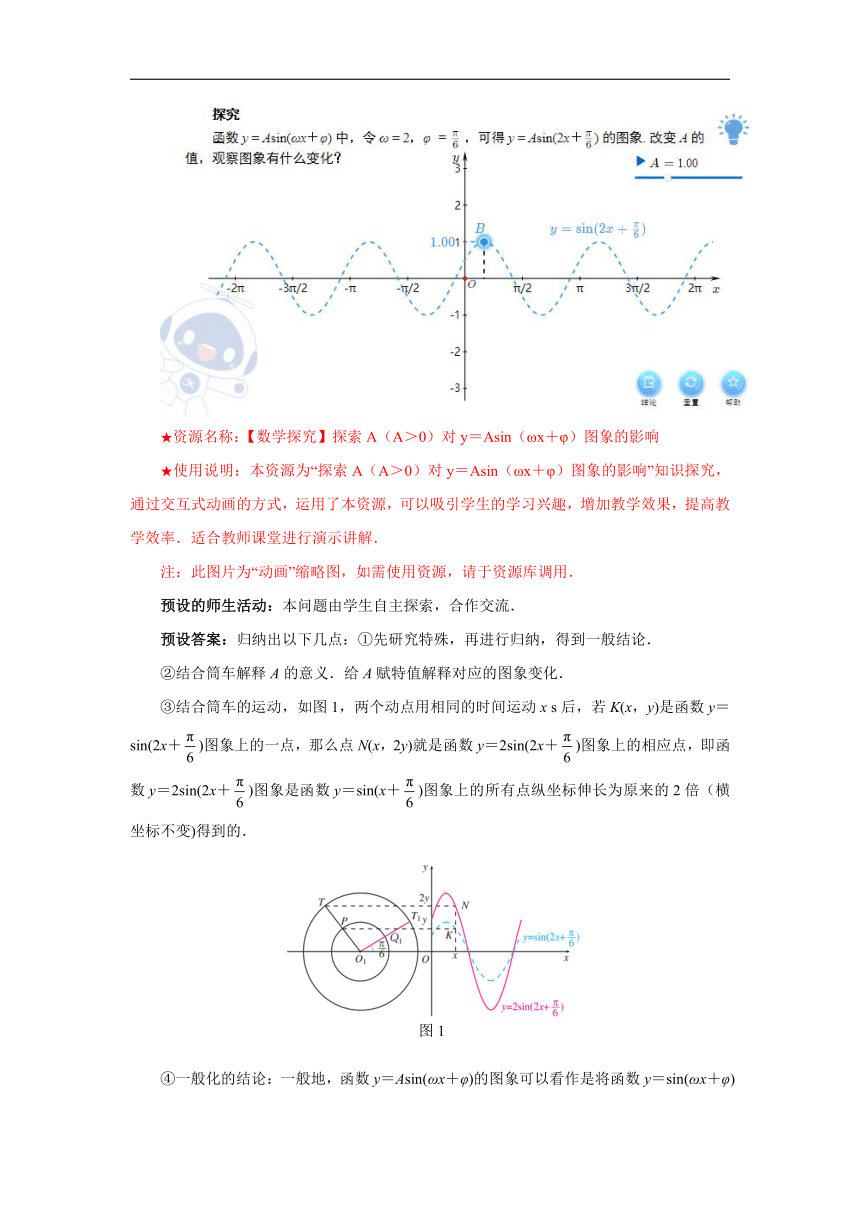
★资源名称:【数学探究】探索A(A>0)对y=Asin(ωx+φ)图象的影响
★使用说明:本资源为“探索A(A>0)对y=Asin(ωx+φ)图象的影响”知识探究,通过交互式动画的方式,运用了本资源,可以吸引学生的学习兴趣,增加教学效果,提高教学效率.适合教师课堂进行演示讲解.
注:此图片为“动画”缩略图,如需使用资源,请于资源库调用.
预设的师生活动:本问题由学生自主探索,合作交流.
预设答案:归纳出以下几点:①先研究特殊,再进行归纳,得到一般结论.
②结合筒车解释A的意义.给A赋特值解释对应的图象变化.
③结合筒车的运动,如图1,两个动点用相同的时间运动x s后,若K(x,y)是函数y=sin(2x+)图象上的一点,那么点N(x,2y)就是函数y=2sin(2x+)图象上的相应点,即函数y=2sin(2x+)图象是函数y=sin(x+)图象上的所有点纵坐标伸长为原来的2倍(横坐标不变)得到的.
(
图1
) (
图1(1)
)
④一般化的结论:一般地,函数y=Asin(ωx+φ)的图象可以看作是将函数y=sin(ωx+φ)的图象上的任意一点的纵坐标伸长(A>1)或缩短(0<A<1)为原来的A倍(横坐标保持不变)得到.从而y=Asin(ωx+φ)的值域是[-A,A],最大值是A,最小值是-A.
设计意图:探究参数A的变化对函数y=Asin(ωx+φ)的图象的影响.学生再次经历“由形导数”“由数释形”的过程,更加突出从点的坐标认识图像变换的规律,体验探究方法,提升思维水平.
7.探索A,ω,φ对函数y=Asin(ωx+φ)的图象的影响
问题7:你能总结一下从函数y=sinx图象出发,通过图象变化得到函数y=Asin(ωx+φ)的图象的过程与方法吗?请你写出来.
★资源名称:【数学探究】画函数y=Asin(ωx+φ)的图象
★使用说明:本资源为“画函数y=Asin(ωx+φ)的图象”知识探究,通过交互式动画的方式,运用了本资源,可以吸引学生的学习兴趣,增加教学效果,提高教学效率.适合教师课堂进行演示讲解.
注:此图片为“动画”缩略图,如需使用资源,请于资源库调用.
预设的师生活动:由学生完成,并展示交流.
预设答案:一般结论:一般地,函数y=Asin(ωx+φ)的图象,可以用下面的方法得到:先画出函数y=sin x的图象;再把正弦曲线上所有点向左(φ>0)或向右(φ<0)平移|φ|个长度单位得到y=sin(x+φ)的图象;然后把曲线上各点的横坐标变为原来的倍(纵坐标不变)得到y=sin(ωx+φ)的图象;最后把曲线上各点的纵坐标变为原来的A倍(横坐标不变),这时的曲线就是函数y=Asin(ωx+φ)的图象.从而y=Asin(ωx+φ)的值域是[-A,A],最大值是A,最小值是-A.
例1 画出函数的简图.
师生活动:因为刚完成了问题7,所以学生应该先想到根据问题7获得的结论完成.学生先独立思考,然后展示交流,由学生口述其变换过程,教师板书步骤.
预设答案:如图2,先画出函数y=sin x的图象;再把正弦曲线上所有点向左平移个长度单位得到y=sin(x+)的图象;然后把曲线上各点的横坐标变为原来的倍(纵坐标不变)得到y=sin(3x+)的图象;最后把曲线上各点的纵坐标变为原来的2(横坐标不变),这时的曲线就是函数y=2sin(3x+)的图象.
(
图2
)
追问:我们已经知道了该函数的图象的整体样貌.回想正弦函数草图的画法,你能用五点法画出这个函数的图象吗?
预设的师生活动:由学生完成,整体展示.学生可以说出找五个关键点.在教师的追问下,形成通过换元转化,最后找到五个关键点的思路
预设答案:五点作图法的步骤:
第一步,用列表、描点的方法,先画出函数在一个周期内的图象.
T=π,令X=.
列表:
X 0 π 2π
x
y 0 2 0 -2 0
描点画图(图3):
(
图3
)
第二步,将函数在一个周期内的图象拓展在整个定义域内.
设计意图:引导学生从局部的讨论过渡到整体的思考,从特殊的例子归纳概括出一般性的结论,得到从正弦函数的图象出发,通过图象变换得到y=Asin(ωx+φ)图象的过程与方法.同时引出“五点法”作图,并从两种方法的联系来加深学生对y=Asin(ωx+φ)图象的认识.
(
图4
)例2 如图4,摩天轮是一种大型转轮状的机械建筑设施,游客坐在摩天轮的座舱里慢慢地往上转,可以从高处俯瞰四周景色.某摩天轮最高点距地面高度为120 m,转盘直径为110 m,设置有48个座舱,开启后按逆时针方向匀速旋转,游客在座舱转到离地面最近的位置进舱,转一周大约需要30 min.
(1)游客甲坐上摩天轮的座舱,开始转动t min后离地面的高度为H m,求在转动一周的过程中,H关于t的函数解析式;
(2)求游客甲在开始转动5 min后离地面的高度;
(3)若甲、乙两人分别坐在两个相邻的座舱里,在运行一周的过程中,求两人距离地面的高度差的最大值(精确到0.1).
预设的师生活动:学生讨论,然后回答.
追问:你打算选择什么函数模型来刻画这个实际问题?为什么?
预设答案:摩天轮上座舱运动可以近似地看作是质点在圆周上做匀速旋转,在旋转过程中,游客距离地面的高度H呈现周而复始的变化,因此可以考虑用三角函数模型来刻画.
(
图5
)如图5,设座舱距离地面最近的位置为点P,以轴心O为原点,与地面平行的直线为x轴建立直角坐标系.
(1)设t=0 min时,游客甲位于点P(0,-55),以OP为终边的角为; 根据摩天轮转一周大约需要30 min,可知座舱转动的角速度约为 rad/min,由题意可得
.
(2)当t=5时,.
(3)甲、乙两人的位置分别用点A,B表示,则.经过t min后甲距离地面的高度为,点B相对于点A始终落后rad,此时乙距离地面的高度为.则甲、乙距离地面的高度差
当(或),即t≈7.8(或22.8)时,
h的最大值为110 sin≈7.2 m.
设计意图:本例与5.6.1小节开篇的筒车问题相呼应,进一步体会圆周运动与三角函数模型之间的内在联系,感受数学建模思想,体现数学的综合运用和实际应用,也是对知识学习效果的一次检测.
(三)归纳小结
问题8:(1)本单元我们研究了哪一类问题?研究的路径是怎样的?
预设答案:
(2)在研究函数y=Asin(ωx+φ)图象的过程中,哪些思想方法值得总结?
预设答案:首先,与二次函数类比的基础上初步形成对函数y=Asin(ωx+φ)的图象进行研究的路径.在这个过程中,是基于特殊情况的分析,再观察多个具体值对函数图象影响的基础上概括出一般化的结论,然后从函数y=sin x的图象经过图象变换得到函数y=Asin(ωx+φ)的图象,得到了一般原则,体现了类比思想和有特殊到一般的数学思想.
设计意图:梳理核心知识和研究过程,以及体现的数学思想和方法,加深学生对数学建模的过程与方法.
(四)布置作业
教科书习题5.6第1,2,3,4,5,6,7题.
(五)目标检测设计
画出函数在长度为一个周期的闭区间上的简图.
预设答案:
设计意图:熟悉正弦型函数简图的作法,为此类函数的应用打好基础.
教学设计
(
教学目标
)
1.掌握参数A对函数y=Asin(ωx+φ)图象的影响,理解参数A在圆周运动中的实际意义,掌握这个函数的性质,发展数学抽象、逻辑推理与直观想象的素养.
2.理解从正弦曲线到函数y=Asin(ωx+φ)图象的变换过程,能用五点(作图)法画函数y=Asin(ωx+φ)图象.
3.会运用函数y=Asin(ωx+φ)的图象与性质解决简单的数学问题和实际问题.
(
教学重难点
)
教学重点:参数A对函数y=Asin(ωx+φ)图象的影响,以及从从正弦曲线到函数y=Asin(ωx+φ)图象的变换过程..
教学难点:从正弦曲线经过图象变换得到函数y=Asin(ωx+φ)图象.
(
课前准备
)
Geogebra软件、PPT课件.借助Geogebra软件,通过作动画可以演示参数A,φ,ω对函数y=Asin(ωx+φ)图象的影响.
资源引用:【数学探究】探索A(A>0)对y=Asin(ωx+φ)图象的影响
【数学探究】画函数y=Asin(ωx+φ)的图象
(
教学过程
)
(一)整体感知
引导语:通过上节课的学习,我们从实际问题出发,建立了一个新的函数y=Asin(ωx+φ),并按照函数的研究套路,研究了该函数的图象中的部分问题.现在继续上一节课的研究.
(二)新知探究
6.探索A(A>0)对函数y=Asin(ωx+φ)的图象的影响
问题6:当参数A变化时,对函数y=Asin(ωx+φ)图象有什么影响?类比ω与φ的研究方法,你计划怎样进行研究?
★资源名称:【数学探究】探索A(A>0)对y=Asin(ωx+φ)图象的影响
★使用说明:本资源为“探索A(A>0)对y=Asin(ωx+φ)图象的影响”知识探究,通过交互式动画的方式,运用了本资源,可以吸引学生的学习兴趣,增加教学效果,提高教学效率.适合教师课堂进行演示讲解.
注:此图片为“动画”缩略图,如需使用资源,请于资源库调用.
预设的师生活动:本问题由学生自主探索,合作交流.
预设答案:归纳出以下几点:①先研究特殊,再进行归纳,得到一般结论.
②结合筒车解释A的意义.给A赋特值解释对应的图象变化.
③结合筒车的运动,如图1,两个动点用相同的时间运动x s后,若K(x,y)是函数y=sin(2x+)图象上的一点,那么点N(x,2y)就是函数y=2sin(2x+)图象上的相应点,即函数y=2sin(2x+)图象是函数y=sin(x+)图象上的所有点纵坐标伸长为原来的2倍(横坐标不变)得到的.
(
图1
) (
图1(1)
)
④一般化的结论:一般地,函数y=Asin(ωx+φ)的图象可以看作是将函数y=sin(ωx+φ)的图象上的任意一点的纵坐标伸长(A>1)或缩短(0<A<1)为原来的A倍(横坐标保持不变)得到.从而y=Asin(ωx+φ)的值域是[-A,A],最大值是A,最小值是-A.
设计意图:探究参数A的变化对函数y=Asin(ωx+φ)的图象的影响.学生再次经历“由形导数”“由数释形”的过程,更加突出从点的坐标认识图像变换的规律,体验探究方法,提升思维水平.
7.探索A,ω,φ对函数y=Asin(ωx+φ)的图象的影响
问题7:你能总结一下从函数y=sinx图象出发,通过图象变化得到函数y=Asin(ωx+φ)的图象的过程与方法吗?请你写出来.
★资源名称:【数学探究】画函数y=Asin(ωx+φ)的图象
★使用说明:本资源为“画函数y=Asin(ωx+φ)的图象”知识探究,通过交互式动画的方式,运用了本资源,可以吸引学生的学习兴趣,增加教学效果,提高教学效率.适合教师课堂进行演示讲解.
注:此图片为“动画”缩略图,如需使用资源,请于资源库调用.
预设的师生活动:由学生完成,并展示交流.
预设答案:一般结论:一般地,函数y=Asin(ωx+φ)的图象,可以用下面的方法得到:先画出函数y=sin x的图象;再把正弦曲线上所有点向左(φ>0)或向右(φ<0)平移|φ|个长度单位得到y=sin(x+φ)的图象;然后把曲线上各点的横坐标变为原来的倍(纵坐标不变)得到y=sin(ωx+φ)的图象;最后把曲线上各点的纵坐标变为原来的A倍(横坐标不变),这时的曲线就是函数y=Asin(ωx+φ)的图象.从而y=Asin(ωx+φ)的值域是[-A,A],最大值是A,最小值是-A.
例1 画出函数的简图.
师生活动:因为刚完成了问题7,所以学生应该先想到根据问题7获得的结论完成.学生先独立思考,然后展示交流,由学生口述其变换过程,教师板书步骤.
预设答案:如图2,先画出函数y=sin x的图象;再把正弦曲线上所有点向左平移个长度单位得到y=sin(x+)的图象;然后把曲线上各点的横坐标变为原来的倍(纵坐标不变)得到y=sin(3x+)的图象;最后把曲线上各点的纵坐标变为原来的2(横坐标不变),这时的曲线就是函数y=2sin(3x+)的图象.
(
图2
)
追问:我们已经知道了该函数的图象的整体样貌.回想正弦函数草图的画法,你能用五点法画出这个函数的图象吗?
预设的师生活动:由学生完成,整体展示.学生可以说出找五个关键点.在教师的追问下,形成通过换元转化,最后找到五个关键点的思路
预设答案:五点作图法的步骤:
第一步,用列表、描点的方法,先画出函数在一个周期内的图象.
T=π,令X=.
列表:
X 0 π 2π
x
y 0 2 0 -2 0
描点画图(图3):
(
图3
)
第二步,将函数在一个周期内的图象拓展在整个定义域内.
设计意图:引导学生从局部的讨论过渡到整体的思考,从特殊的例子归纳概括出一般性的结论,得到从正弦函数的图象出发,通过图象变换得到y=Asin(ωx+φ)图象的过程与方法.同时引出“五点法”作图,并从两种方法的联系来加深学生对y=Asin(ωx+φ)图象的认识.
(
图4
)例2 如图4,摩天轮是一种大型转轮状的机械建筑设施,游客坐在摩天轮的座舱里慢慢地往上转,可以从高处俯瞰四周景色.某摩天轮最高点距地面高度为120 m,转盘直径为110 m,设置有48个座舱,开启后按逆时针方向匀速旋转,游客在座舱转到离地面最近的位置进舱,转一周大约需要30 min.
(1)游客甲坐上摩天轮的座舱,开始转动t min后离地面的高度为H m,求在转动一周的过程中,H关于t的函数解析式;
(2)求游客甲在开始转动5 min后离地面的高度;
(3)若甲、乙两人分别坐在两个相邻的座舱里,在运行一周的过程中,求两人距离地面的高度差的最大值(精确到0.1).
预设的师生活动:学生讨论,然后回答.
追问:你打算选择什么函数模型来刻画这个实际问题?为什么?
预设答案:摩天轮上座舱运动可以近似地看作是质点在圆周上做匀速旋转,在旋转过程中,游客距离地面的高度H呈现周而复始的变化,因此可以考虑用三角函数模型来刻画.
(
图5
)如图5,设座舱距离地面最近的位置为点P,以轴心O为原点,与地面平行的直线为x轴建立直角坐标系.
(1)设t=0 min时,游客甲位于点P(0,-55),以OP为终边的角为; 根据摩天轮转一周大约需要30 min,可知座舱转动的角速度约为 rad/min,由题意可得
.
(2)当t=5时,.
(3)甲、乙两人的位置分别用点A,B表示,则.经过t min后甲距离地面的高度为,点B相对于点A始终落后rad,此时乙距离地面的高度为.则甲、乙距离地面的高度差
当(或),即t≈7.8(或22.8)时,
h的最大值为110 sin≈7.2 m.
设计意图:本例与5.6.1小节开篇的筒车问题相呼应,进一步体会圆周运动与三角函数模型之间的内在联系,感受数学建模思想,体现数学的综合运用和实际应用,也是对知识学习效果的一次检测.
(三)归纳小结
问题8:(1)本单元我们研究了哪一类问题?研究的路径是怎样的?
预设答案:
(2)在研究函数y=Asin(ωx+φ)图象的过程中,哪些思想方法值得总结?
预设答案:首先,与二次函数类比的基础上初步形成对函数y=Asin(ωx+φ)的图象进行研究的路径.在这个过程中,是基于特殊情况的分析,再观察多个具体值对函数图象影响的基础上概括出一般化的结论,然后从函数y=sin x的图象经过图象变换得到函数y=Asin(ωx+φ)的图象,得到了一般原则,体现了类比思想和有特殊到一般的数学思想.
设计意图:梳理核心知识和研究过程,以及体现的数学思想和方法,加深学生对数学建模的过程与方法.
(四)布置作业
教科书习题5.6第1,2,3,4,5,6,7题.
(五)目标检测设计
画出函数在长度为一个周期的闭区间上的简图.
预设答案:
设计意图:熟悉正弦型函数简图的作法,为此类函数的应用打好基础.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
