解决不等式恒成立问题的常见方法
图片预览


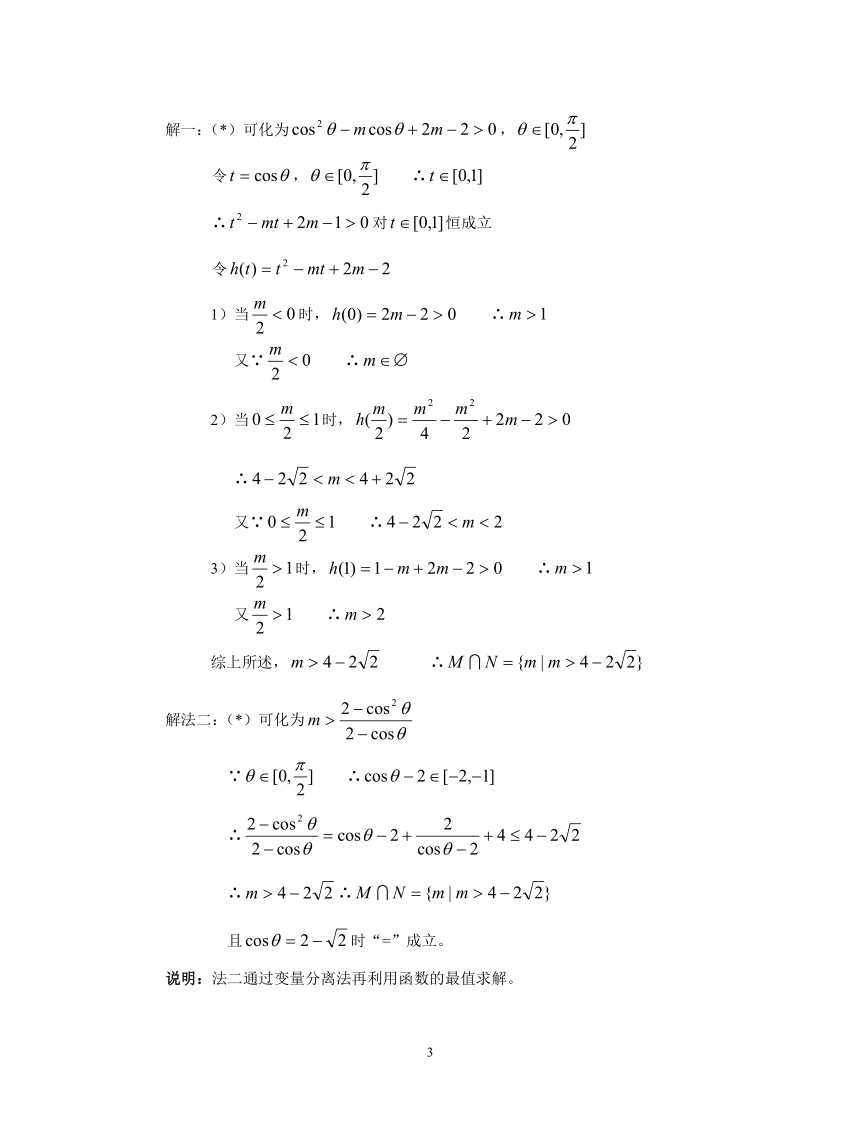
文档简介
解决不等式恒成立问题的常见方法
宁海中学 杨丹阳
像函数一样,近十多年高考几乎考遍了不等式的所有知识点和各种主要题型,不等式的各种主要应用也时有涉猎,解证不等式是考查的重点,经常与一次函数、二次函数、指数函数、对数函数等相结合,近几年在函数、不等式、数列、向量、解析几何各种知识网络的交汇处命题,重点考查不等式知识,试题的立意高、难度大、综合性强。本文重点研究不等式中常见类型——恒成立问题的解决方法,供广大师生参考。
1、判别式法:
当试题中出现最高次为二次时,常常通过判别式去研究解决,这就是判别式法。
例1、已知函数。
⑴若的定义域为R,求实数的取值范围;
⑵若的值域为R,求实数的取值范围。
解:⑴依题意:对一切恒成立。
当时的充要条件是,
解得或
⑵依题意,只要能取到内的所有值,
则的值域为R。
∴,解得
又当时,符合题意。
∴的取值范围是
说明:二次项系数含字母时,注意分类讨论。
例2、(2005年浙江·理)已知向量,,满足:对注意,恒有
,则( )
A、 B、 C、 D、
分析:向量模的问题常常通过,即可转化为二次不等式研究。
解:由题可得,
∴
∵ ∴,对恒成立 ∴
∵ ∴ ∴ ∴ ∴应选C
2、函数最值法:
这是最重要的方法,它常常通过构造函数求最值,有时再借助导数研究函数的单调性或最值,从而解决问题。
例3、已知奇函数在上有意义,且在上是增函数,,又有函数,。若集合,集合。求:⑴;⑵求的解。
解:⑴∵是奇函数, ∴
又∵在上是增函数 ∴在上也是增函数
∴的解集得或
⑵∵又由⑴可得或
又∵ ∴
∴(*),对恒成立。
解一:(*)可化为,
令, ∴
∴对恒成立
令
1)当时, ∴
又∵ ∴
2)当时,
∴
又∵ ∴
3)当时, ∴
又 ∴
综上所述, ∴
解法二:(*)可化为
∵ ∴
∴
∴∴
且时“=”成立。
说明:法二通过变量分离法再利用函数的最值求解。
例4、数列中,,,且满足,设,,是否存在最大的整数,使得任意,均有成立?若存在,求出的值;若不存在,请说明理由。
解:∵
∴
∴是等差数列,公差
∴
∵
∴递增 ∴
∵恒成立 ∴ ∴
∵ ∴的最大值为7。
例5、已知在区间上是增函数。
⑴求实数的值组成的集合A;
⑵设关于的方程的两个非零实根为、。试问:是否存在实数,使得不等式对任意及恒成立?若存在,求的取值范围;若不存在,请说明理由。
解:⑴ ∵在上是增函数
∴对恒成立,即对恒成立。
设,,
①。
∵对,是连续函数,且只有当时,以及当时,
∴
⑵由,得。 ∵
∴、是方程的两非零实根,有,,
从而
∵ ∴
要使不等式对任意及恒成立,
当且化当对任意恒成立,
即对任意恒成立或。
所以,存在实数,使不等式对任意及恒成立,其,取值范围是或。
评注:自变量、参数往往是相对的,本题根据需要可把函数看作关于的函数,利用单调性,只要得到最大值,最小值均大于0,从而避免讨论解决问题。
例6、函数在区间内可导,导函数是减函数,且。设,是曲线在点处的切线方程,并设函数。
⑴用、、表示;
⑵证明:当时,。
解:⑴由这可知,
∴
⑵证明:令
则,。
因为递减,所以递增,因此,当时,;
当时,。
所以是唯一的极值点,且是极小值点,可知的最小值为0,因
此,即。
说明:近几年高考数学题对新增内容的要求一年比一年高,例如本题和上题用导数研究函数的性质,一举打破了多年函数考题的传统模式。因此,在复习中引起重视。
3、数形结合法:
当不等式中同时出现两种类型的函数形式时,直接解不等式很难,而前面介绍的两种方法均不适用时,不妨从形上考虑,就是说作出函数的图象以行论数,达到解题效果,这就是数形结合法。
例7、若不等式对恒成立,求实数的取值范围。
解:原不等式为,设,
∵,而 ∴
作出在内的图象,如下图所示,
∵ ∴
当的图象经过点A ∴
∵当时,
∴图象按如图虚线位置变化
∴
4、利用不等式性质求解:
对于一次函数或二次函数在某一区间上恒成立问题,通过待定系数法,把未知的转化为已知的考虑,再利用不等式性质或线性规划知识研究。
例8、二次函数,对恒有。求证:。
证明:依题意:,,
令,则
∴
∴
∴
即
说明:如对含绝对值不等式恒成立问题,结合不等式的性质求解。
以上就是本人对不等式恒成立问题的一点心得与体会,在这些方法中始终贯穿了数学中的几大重要思想方法:化归思想、函数与方程思想、数形结合思想、不等式思想、分类讨论思想,这些方法不仅有独到的功能,而且可以培养我们的思维能力和逻辑推理能力,提高解题效率。
x
y
1
A
PAGE
2
宁海中学 杨丹阳
像函数一样,近十多年高考几乎考遍了不等式的所有知识点和各种主要题型,不等式的各种主要应用也时有涉猎,解证不等式是考查的重点,经常与一次函数、二次函数、指数函数、对数函数等相结合,近几年在函数、不等式、数列、向量、解析几何各种知识网络的交汇处命题,重点考查不等式知识,试题的立意高、难度大、综合性强。本文重点研究不等式中常见类型——恒成立问题的解决方法,供广大师生参考。
1、判别式法:
当试题中出现最高次为二次时,常常通过判别式去研究解决,这就是判别式法。
例1、已知函数。
⑴若的定义域为R,求实数的取值范围;
⑵若的值域为R,求实数的取值范围。
解:⑴依题意:对一切恒成立。
当时的充要条件是,
解得或
⑵依题意,只要能取到内的所有值,
则的值域为R。
∴,解得
又当时,符合题意。
∴的取值范围是
说明:二次项系数含字母时,注意分类讨论。
例2、(2005年浙江·理)已知向量,,满足:对注意,恒有
,则( )
A、 B、 C、 D、
分析:向量模的问题常常通过,即可转化为二次不等式研究。
解:由题可得,
∴
∵ ∴,对恒成立 ∴
∵ ∴ ∴ ∴ ∴应选C
2、函数最值法:
这是最重要的方法,它常常通过构造函数求最值,有时再借助导数研究函数的单调性或最值,从而解决问题。
例3、已知奇函数在上有意义,且在上是增函数,,又有函数,。若集合,集合。求:⑴;⑵求的解。
解:⑴∵是奇函数, ∴
又∵在上是增函数 ∴在上也是增函数
∴的解集得或
⑵∵又由⑴可得或
又∵ ∴
∴(*),对恒成立。
解一:(*)可化为,
令, ∴
∴对恒成立
令
1)当时, ∴
又∵ ∴
2)当时,
∴
又∵ ∴
3)当时, ∴
又 ∴
综上所述, ∴
解法二:(*)可化为
∵ ∴
∴
∴∴
且时“=”成立。
说明:法二通过变量分离法再利用函数的最值求解。
例4、数列中,,,且满足,设,,是否存在最大的整数,使得任意,均有成立?若存在,求出的值;若不存在,请说明理由。
解:∵
∴
∴是等差数列,公差
∴
∵
∴递增 ∴
∵恒成立 ∴ ∴
∵ ∴的最大值为7。
例5、已知在区间上是增函数。
⑴求实数的值组成的集合A;
⑵设关于的方程的两个非零实根为、。试问:是否存在实数,使得不等式对任意及恒成立?若存在,求的取值范围;若不存在,请说明理由。
解:⑴ ∵在上是增函数
∴对恒成立,即对恒成立。
设,,
①。
∵对,是连续函数,且只有当时,以及当时,
∴
⑵由,得。 ∵
∴、是方程的两非零实根,有,,
从而
∵ ∴
要使不等式对任意及恒成立,
当且化当对任意恒成立,
即对任意恒成立或。
所以,存在实数,使不等式对任意及恒成立,其,取值范围是或。
评注:自变量、参数往往是相对的,本题根据需要可把函数看作关于的函数,利用单调性,只要得到最大值,最小值均大于0,从而避免讨论解决问题。
例6、函数在区间内可导,导函数是减函数,且。设,是曲线在点处的切线方程,并设函数。
⑴用、、表示;
⑵证明:当时,。
解:⑴由这可知,
∴
⑵证明:令
则,。
因为递减,所以递增,因此,当时,;
当时,。
所以是唯一的极值点,且是极小值点,可知的最小值为0,因
此,即。
说明:近几年高考数学题对新增内容的要求一年比一年高,例如本题和上题用导数研究函数的性质,一举打破了多年函数考题的传统模式。因此,在复习中引起重视。
3、数形结合法:
当不等式中同时出现两种类型的函数形式时,直接解不等式很难,而前面介绍的两种方法均不适用时,不妨从形上考虑,就是说作出函数的图象以行论数,达到解题效果,这就是数形结合法。
例7、若不等式对恒成立,求实数的取值范围。
解:原不等式为,设,
∵,而 ∴
作出在内的图象,如下图所示,
∵ ∴
当的图象经过点A ∴
∵当时,
∴图象按如图虚线位置变化
∴
4、利用不等式性质求解:
对于一次函数或二次函数在某一区间上恒成立问题,通过待定系数法,把未知的转化为已知的考虑,再利用不等式性质或线性规划知识研究。
例8、二次函数,对恒有。求证:。
证明:依题意:,,
令,则
∴
∴
∴
即
说明:如对含绝对值不等式恒成立问题,结合不等式的性质求解。
以上就是本人对不等式恒成立问题的一点心得与体会,在这些方法中始终贯穿了数学中的几大重要思想方法:化归思想、函数与方程思想、数形结合思想、不等式思想、分类讨论思想,这些方法不仅有独到的功能,而且可以培养我们的思维能力和逻辑推理能力,提高解题效率。
x
y
1
A
PAGE
2
