平行线

4.8 平行线
一、选择题
1．在同一平面内，两条直线可能的位置关系是 （ ）
　 (A) 平行． (B) 相交． (C) 相交或平行． (D) 垂直．
2．判定两角相等，不正确的是 （ ）
（A） 对顶角相等．
（B） 两直线平行，同位角相等．
（C） ∵∠1=∠2，∠2=∠3，∴∠1=∠3．
（D） 两条直线被第三条直线所截，内错角相等．
3．两个角的两边分别平行，其中一个角是60°，则另一个角是 （ ）
　（A）60°． （B）120°．
　（C） 60°或120°． （D） 无法确定．
4．下列语句中正确的是（ ）
（A）不相交的两条直线叫做平行线．　　　　　　　　　　　
（B）过一点有且只有一条直线与已知直线平行．　　　　　　
（C）两直线平行，同旁内角相等．　　　　　　　　　　　　
（D）两条直线被第三条直线所截，同位角相等．
５．下列说法正确的是（　 ）
　 （A）垂直于同一直线的两条直线互相垂直．
　 （B）平行于同一条直线的两条直线互相平行．
　 （C）平面内两个角相等，则他们的两边分别平行．
　 （D）两条直线被第三条直线所截，那么有两对同位角相等．　
６．已知AB∥CD∥EF，BC∥AD，AC平分∠BAD，那么图中与∠AGE相等的角有( )
　（A）5个． （B）4个． （C）3个． （D）2个．　
HYPERLINK "http://" INCLUDEPICTURE "http://cimg./education/0501/25/sx/image004.jpg" \* MERGEFORMATINET
二、填空题
7. 如果a∥b，b∥c，则______∥______，因为________．
8．在同一平面内，如果a⊥b，b⊥c，则a c，因为　　　．
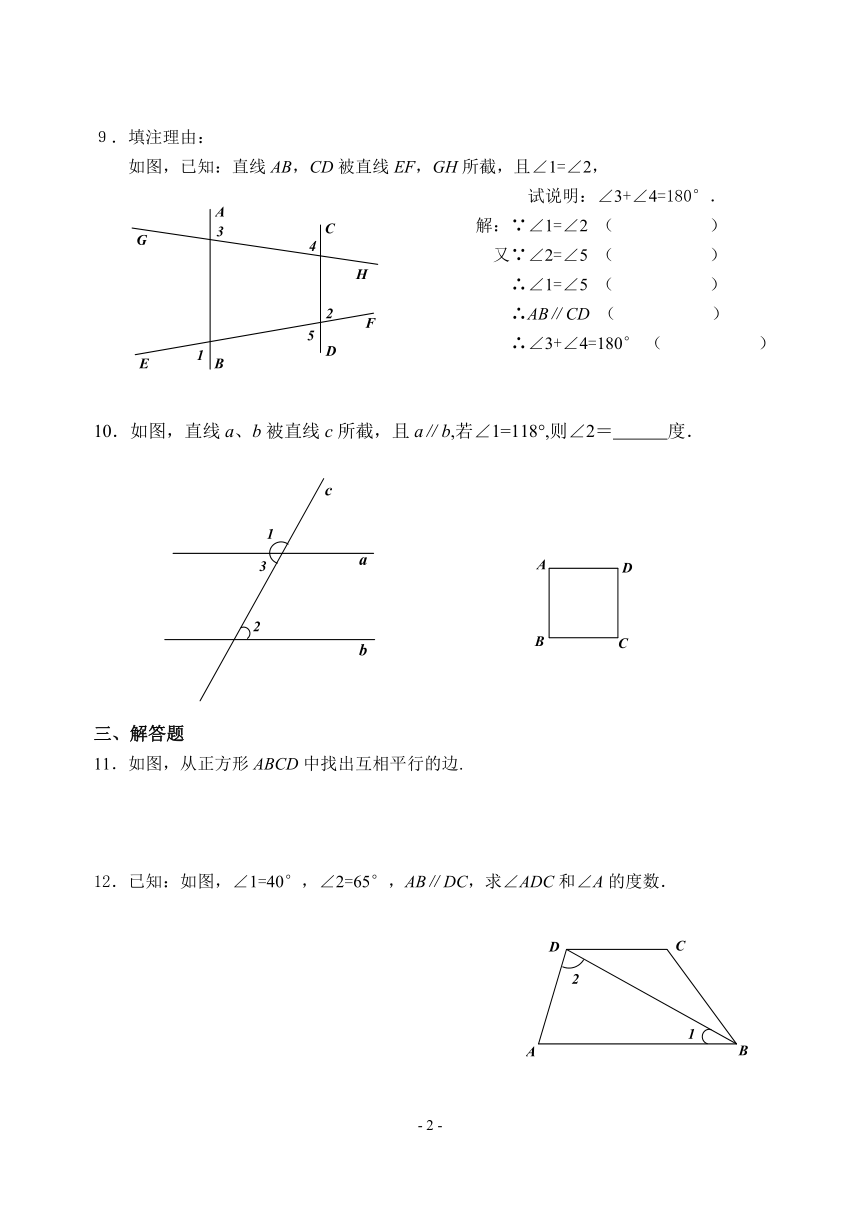
９．填注理由：
如图，已知：直线AB，CD被直线EF，GH所截，且∠1=∠2，
　　 试说明：∠3+∠4=180°．
　 解：∵∠1=∠2 （　　　　　 ）
　　 又∵∠2=∠5 （ 　　　　　）
　　　 ∴∠1=∠5 （　　　　　 ）
　　　 ∴AB∥CD （　　　　　 ）
　　　 ∴∠3+∠4=180° （　　　　　 ）
10．如图，直线a、b被直线c所截，且a∥b,若∠1=118°,则∠2＝　　　度．　
三、解答题
11．如图，从正方形ABCD中找出互相平行的边.
12．已知：如图，∠1=40°，∠2=65°，AB∥DC，求∠ADC和∠A的度数．
　 ( http: / / )
13．已知：如图AD∥BE，∠1=∠2，求证：∠A=∠E．
14．如图，根据下列条件，可以判定哪两条直线平行？并说明判定的依据．
　　（1）∠1=∠C　　　
（2）∠2=∠4
　　（3）∠2+∠5=180°　
（4）∠3=∠B　　
（5）∠6=∠2
15．已知：如图，∠1=∠4，∠2=∠3，求证：// ．
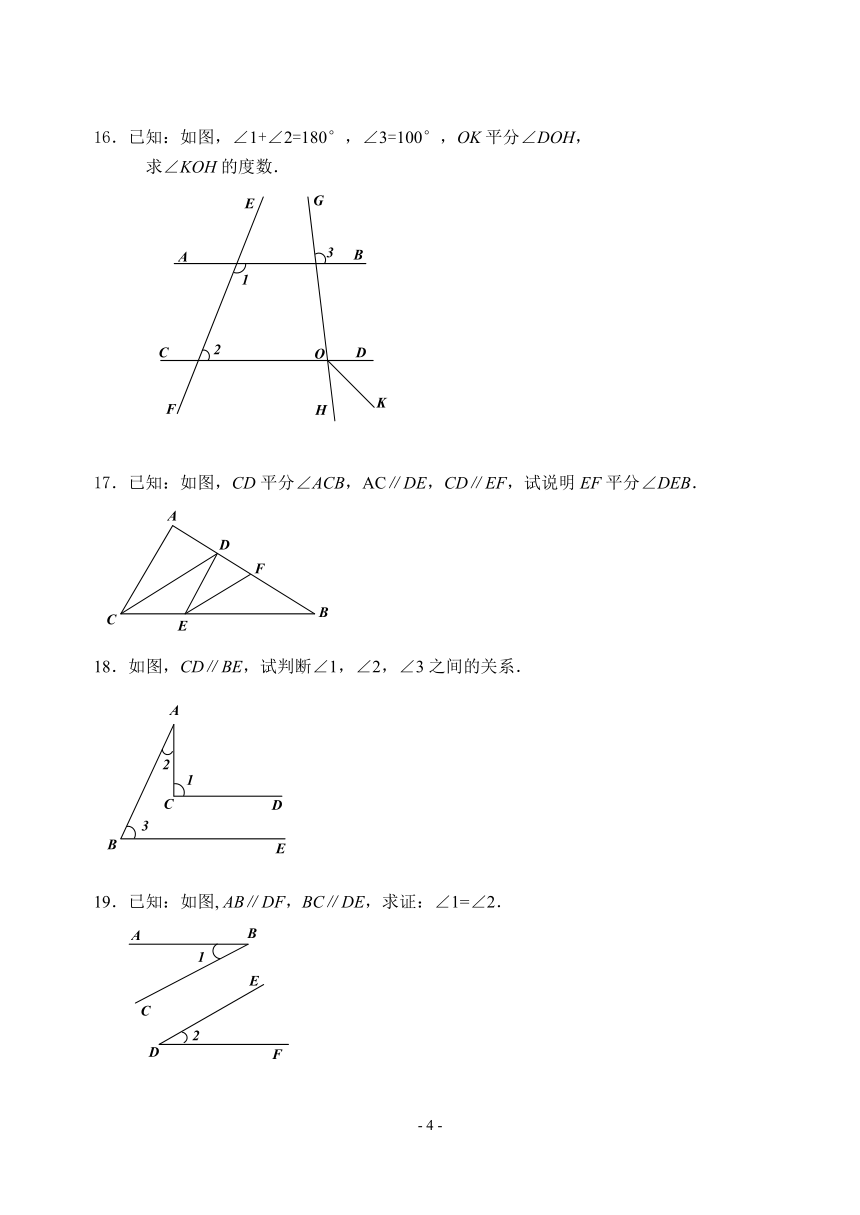
16．已知：如图，∠1+∠2=180°，∠3=100°，OK平分∠DOH，
　　　求∠KOH的度数．
　　　 ( http: / / )
17．已知：如图，CD平分∠ACB，AC∥DE，CD∥EF，试说明EF平分∠DEB．
18．如图，CD∥BE，试判断∠1，∠2，∠3之间的关系．
( http: / / )
19．已知：如图, AB∥DF，BC∥DE，求证：∠1=∠2．
答案:
一、1.C 2.D 3.C 4.B 5.B 6.A
二、7.a∥c平行于同一条直线的两条直线平行
8.a∥c在同一平面内，垂直于同一条直线的两条直线平行
9.已知 对顶角相等 等量代换 同位角相等两直线平行 两直线平行同旁内角互补 10. 62°
三、11.AD∥BC AB∥CD 12. ∠ADC=105°, ∠A=75°
13.∵∠1=∠2 ∴AC∥DE ∴∠A+∠ADE=180°
∵AD∥BE ∴∠ADE+∠E=180° ∴∠A=∠E
14.⑴∵∠1=∠C ∴AC∥DF(同位角相等,两直线平行)
⑵∵∠2=∠4 ∴AB∥DE(内错角相等,两直线平行)
⑶∵∠2+∠5=180° ∴AC∥DF(同旁内角互补,两直线平行)
⑷∵∠3=∠B ∴DE∥AB(同位角相等,两直线平行)
⑸∵∠6=∠2 ∴FD∥AC(内错角相等,两直线平行)
15. ∵∠1=∠4 ∴∥
∵∠2=∠3 ∴∥ ∴∥
16. ∠KOH=40°
17. ∵AC∥DE ∴∠ACB=∠DEB ∵EF∥CD ∴∠FEB=∠DCB
∵∠DCB=∠ACD ∴∠FEB=∠DEF ∴EF平分∠DEB.
18.提示: 过A作AF∥CD ∠1=∠2+∠3
19.提示: 连结BD
www.1230.org 初中数学资源网 收集整理
4.8 平行线讲学稿
一、学习目标：
认识平行线的特征，并能灵活地利用平行线的三个特征解决问题；并能根据图中已知条件通过简单说理，得出欲求结果。
二、教学重点：平行线的三个特征，运用这三个特征解决问题;
难点：平行线的识别与特征的综合应用.
预习内容：课本第172到174页.
预习自测：
1．两条平行线线被第三条直线所截， 相等。
简单地说，就是 _______.
即：如果AB∥CD，根据 ，那么∠1=∠2.
2．两条平行线线被第三条直线所截， 相等。
简单地说，就是 ____________________.
即：如果AB∥CD，根据 ，那么∠2=∠3.
3两条平行线线被第三条直线所截， 互补。
简单地说，就是 __________________________.
即：如果AB∥CD，根据 ，那么∠2+∠4=180°
尝试练习一：
如图，已知直线a∥b，∠1=60°，求∠2的度数。
尝试练习二
1．如图再四边行ABCD中，已知AB∥CD，∠B=50°
求∠C的度数。能否求得∠A的度数？
2．已知AB∥CD，∠AMN=(5x-36) °, ∠MND=(3x+16) °
求∠AMN，∠MND的度数
尝试练习三：
1． 如图：已知∠FDE=∠ABF，BF∥CE,你能否说明DF∥AC,
写出说明过程
2． 已知AB∥CD，∠B+∠D=180°,那么直线BC与ED的位置关系如何？
请说明理由。
课堂训练：
1． 如图：（1）如果AD∥BC,那么根据
，可得∠1= ；
（2）如果AB∥CD,那么根据
，可得∠1= ；
2． 如果两个角的一边在同一条直线上，另一条边互相
平行，那么，这两个角的关系是-----------------（ ）
A．相等 B.互补 C.相等 且互补 D.相等 或互补
3． 如图，若DE∥BC，AB∥EF，∠ADE=60°，
那么∠EFC等于多少度？
4． 如图，已知AB∥CD，∠A=∠C，
那么AD与BC平行吗？为什么？
D
C
B
l
A
b
a
（第6题图）
- 2 -