2.2 圆的对称性习题 2023-2024学年苏科版九年级数学上册(无答案)
文档属性
| 名称 | 2.2 圆的对称性习题 2023-2024学年苏科版九年级数学上册(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 180.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-05 18:42:18 | ||
图片预览

文档简介
2.2圆的对称性
一.选择题
1.如图,AB为⊙O的弦,半径OC⊥AB于点D,若AB=8,CD=2,则OB的长是( )
A.3 B.4 C.5 D.6
2.如图,⊙O的半径为5,弦AB=6,P是弦AB上的一个动点(不与A、B重合),下列符合条件的OP的值可以是( )
A.3.1 B.4.2 C.5.3 D.6.4
3.如图所示,⊙O的直径为20,弦AB的长度是16,ON⊥AB,垂足为N,则ON的长度为( )
A.4 B.6 C.8 D.10
4.如图,AB为⊙O的直径,AB=10,C,D为⊙O上两动点(C,D不与A,B重合),且CD为定长,CE⊥AB于E,M是CD的中点,则EM的最大值为( )
A.4 B.4.5 C.5 D.6
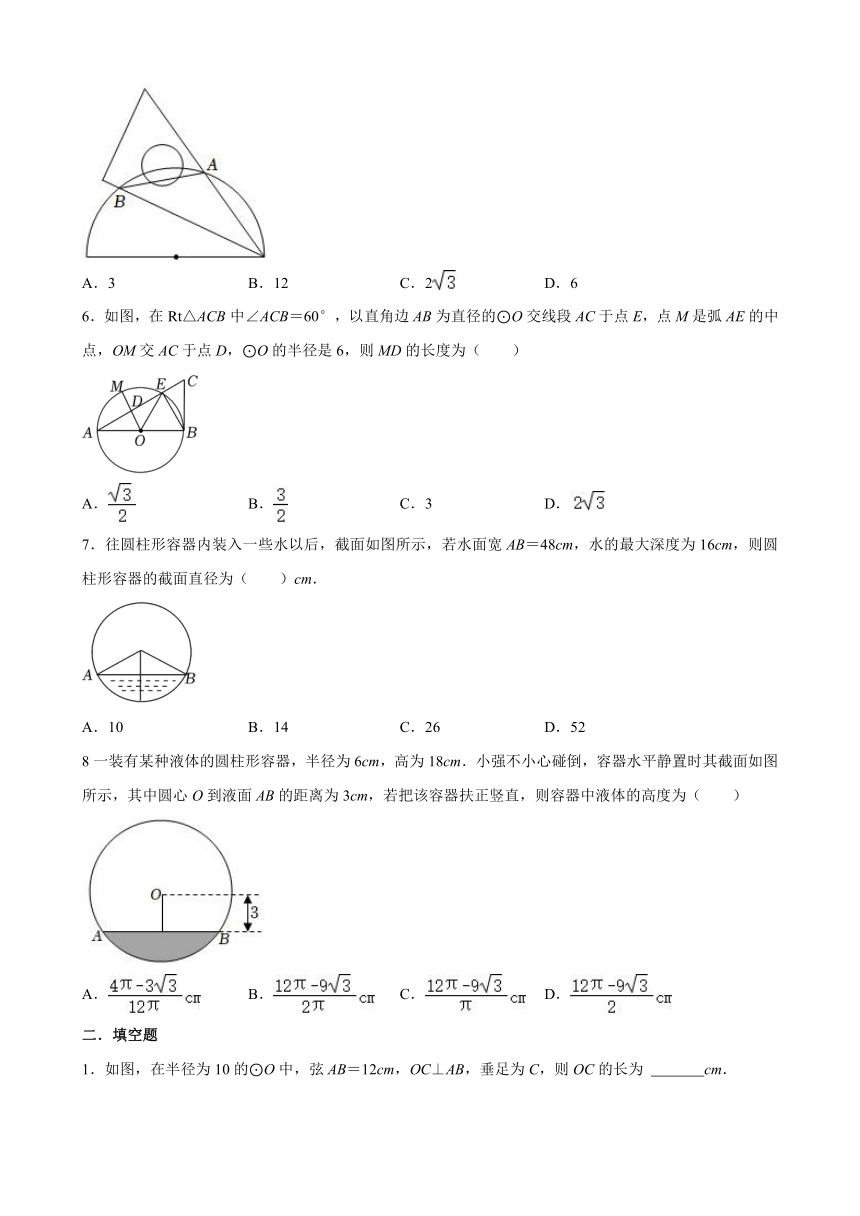
5.如图,半圆的半径为6,将三角板的30°角顶点放在半圆上,这个角的两边分别与半圆相交于点A,B,则AB的长度为( )
A.3 B.12 C.2 D.6
6.如图,在Rt△ACB中∠ACB=60°,以直角边AB为直径的⊙O交线段AC于点E,点M是弧AE的中点,OM交AC于点D,⊙O的半径是6,则MD的长度为( )
A. B. C.3 D.
7.往圆柱形容器内装入一些水以后,截面如图所示,若水面宽AB=48cm,水的最大深度为16cm,则圆柱形容器的截面直径为( )cm.
A.10 B.14 C.26 D.52
8一装有某种液体的圆柱形容器,半径为6cm,高为18cm.小强不小心碰倒,容器水平静置时其截面如图所示,其中圆心O到液面AB的距离为3cm,若把该容器扶正竖直,则容器中液体的高度为( )
A. B. C. D.
二.填空题
1.如图,在半径为10的⊙O中,弦AB=12cm,OC⊥AB,垂足为C,则OC的长为 cm.
2.如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8,OF=,则OE的长为
3.已知⊙O的半径为7,AB是⊙O的弦,点P在弦AB上.若PA=4,PB=6,则OP=
4.如图,AB是⊙O的直径,OD垂直于弦AC于点D,DO的延长线交⊙O于点E.若AC=4,DE=4,则BC的长是( )
5.如图,C为弧AB的中点,CN⊥OB于N,CD⊥OA于M,CD=4cm,则CN= cm.
6.如图,在⊙O中,AB=AC,∠BAC=90°,点P为上任意一点,连接PA,PB,PC,则线段PA,PB,PC之间的数量关系为 .
三.解答题
1.如图为桥洞的形状,其正视图是由圆弧和矩形ABCD构成.O点为所在⊙O的圆心,点O又恰好在AB为水面处.若桥洞跨度CD为8米,拱高(OE⊥弦CD于点F )EF为2米.
(1)求所在⊙O的半径DO;
(2)若河里行驶来一艘正视图为矩形的船,其宽6米,露出水面AB的高度为h米,求船能通过桥洞时的最大高度h.
2.如图,在△ABC中,∠C=90°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E.
(1)若∠A=25°,求的度数;
(2)若BC=9,AC=12,求BD的长.
3.诗句“君到姑苏见,人家尽枕河”所描绘的就是有东方威尼斯之称的水城苏州.小勇要帮忙船夫计算一艘货船是否能够安全通过一座圆弧形的拱桥,现测得桥下水面AB宽度16m时,拱顶高出水平面4m,货船宽12m,船舱顶部为矩形并高出水面3m.
(1)请你帮助小勇求此圆弧形拱桥的半径;
(2)小勇在解决这个问题时遇到困难,请你判断一下,此货船能顺利通过这座拱桥吗?说说你的理由.
4.如图,AC为⊙O的直径,CD为⊙O的弦,BE⊥CD于点E,=.
(1)求证:BE是⊙O的切线.
(2)若AD=4,EC=1,求BD的长.
5.如图,以△AOB的顶点O为圆心,OB为半径作⊙O,交OA于点E,交AB于点D,连接DE,DE∥OB,延长AO交⊙O于点C,连接CB.
(1)求证:=;
(2)若AD=4,AE=CE,求OC的长.
一.选择题
1.如图,AB为⊙O的弦,半径OC⊥AB于点D,若AB=8,CD=2,则OB的长是( )
A.3 B.4 C.5 D.6
2.如图,⊙O的半径为5,弦AB=6,P是弦AB上的一个动点(不与A、B重合),下列符合条件的OP的值可以是( )
A.3.1 B.4.2 C.5.3 D.6.4
3.如图所示,⊙O的直径为20,弦AB的长度是16,ON⊥AB,垂足为N,则ON的长度为( )
A.4 B.6 C.8 D.10
4.如图,AB为⊙O的直径,AB=10,C,D为⊙O上两动点(C,D不与A,B重合),且CD为定长,CE⊥AB于E,M是CD的中点,则EM的最大值为( )
A.4 B.4.5 C.5 D.6
5.如图,半圆的半径为6,将三角板的30°角顶点放在半圆上,这个角的两边分别与半圆相交于点A,B,则AB的长度为( )
A.3 B.12 C.2 D.6
6.如图,在Rt△ACB中∠ACB=60°,以直角边AB为直径的⊙O交线段AC于点E,点M是弧AE的中点,OM交AC于点D,⊙O的半径是6,则MD的长度为( )
A. B. C.3 D.
7.往圆柱形容器内装入一些水以后,截面如图所示,若水面宽AB=48cm,水的最大深度为16cm,则圆柱形容器的截面直径为( )cm.
A.10 B.14 C.26 D.52
8一装有某种液体的圆柱形容器,半径为6cm,高为18cm.小强不小心碰倒,容器水平静置时其截面如图所示,其中圆心O到液面AB的距离为3cm,若把该容器扶正竖直,则容器中液体的高度为( )
A. B. C. D.
二.填空题
1.如图,在半径为10的⊙O中,弦AB=12cm,OC⊥AB,垂足为C,则OC的长为 cm.
2.如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8,OF=,则OE的长为
3.已知⊙O的半径为7,AB是⊙O的弦,点P在弦AB上.若PA=4,PB=6,则OP=
4.如图,AB是⊙O的直径,OD垂直于弦AC于点D,DO的延长线交⊙O于点E.若AC=4,DE=4,则BC的长是( )
5.如图,C为弧AB的中点,CN⊥OB于N,CD⊥OA于M,CD=4cm,则CN= cm.
6.如图,在⊙O中,AB=AC,∠BAC=90°,点P为上任意一点,连接PA,PB,PC,则线段PA,PB,PC之间的数量关系为 .
三.解答题
1.如图为桥洞的形状,其正视图是由圆弧和矩形ABCD构成.O点为所在⊙O的圆心,点O又恰好在AB为水面处.若桥洞跨度CD为8米,拱高(OE⊥弦CD于点F )EF为2米.
(1)求所在⊙O的半径DO;
(2)若河里行驶来一艘正视图为矩形的船,其宽6米,露出水面AB的高度为h米,求船能通过桥洞时的最大高度h.
2.如图,在△ABC中,∠C=90°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E.
(1)若∠A=25°,求的度数;
(2)若BC=9,AC=12,求BD的长.
3.诗句“君到姑苏见,人家尽枕河”所描绘的就是有东方威尼斯之称的水城苏州.小勇要帮忙船夫计算一艘货船是否能够安全通过一座圆弧形的拱桥,现测得桥下水面AB宽度16m时,拱顶高出水平面4m,货船宽12m,船舱顶部为矩形并高出水面3m.
(1)请你帮助小勇求此圆弧形拱桥的半径;
(2)小勇在解决这个问题时遇到困难,请你判断一下,此货船能顺利通过这座拱桥吗?说说你的理由.
4.如图,AC为⊙O的直径,CD为⊙O的弦,BE⊥CD于点E,=.
(1)求证:BE是⊙O的切线.
(2)若AD=4,EC=1,求BD的长.
5.如图,以△AOB的顶点O为圆心,OB为半径作⊙O,交OA于点E,交AB于点D,连接DE,DE∥OB,延长AO交⊙O于点C,连接CB.
(1)求证:=;
(2)若AD=4,AE=CE,求OC的长.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
