2023-2024学年华东师大版八年级数学上册13.2 三角形全等的判定 同步特训(含解析)
文档属性
| 名称 | 2023-2024学年华东师大版八年级数学上册13.2 三角形全等的判定 同步特训(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 294.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-05 19:22:55 | ||
图片预览


文档简介
13.2 三角形全等的判定(同步特训)
华东师大新版八年级上学期数学
一.选择题(共8小题)
1.如图是两个全等三角形,图中的字母表示三角形的边长,则∠1的度数是( )
A.54° B.56° C.60° D.66°
2.在△ABC中,AD平分∠BAC,∠B=2∠ADB,AB=3,CD=5,则AC的长为( )
A.6 B.7 C.8 D.9
3.如图,有一块三角形玻璃,小明不小心将它打破.带上这块玻璃,能配成同样大小的一块,其理由是( )
A.SSS B.ASA C.SAS D.HL
4.如图,点B,C,E在同一条直线上,∠B=∠E=∠ACF=60°,AB=CE,则与线段BC相等的线段是( )
A.AC B.AF C.CF D.EF
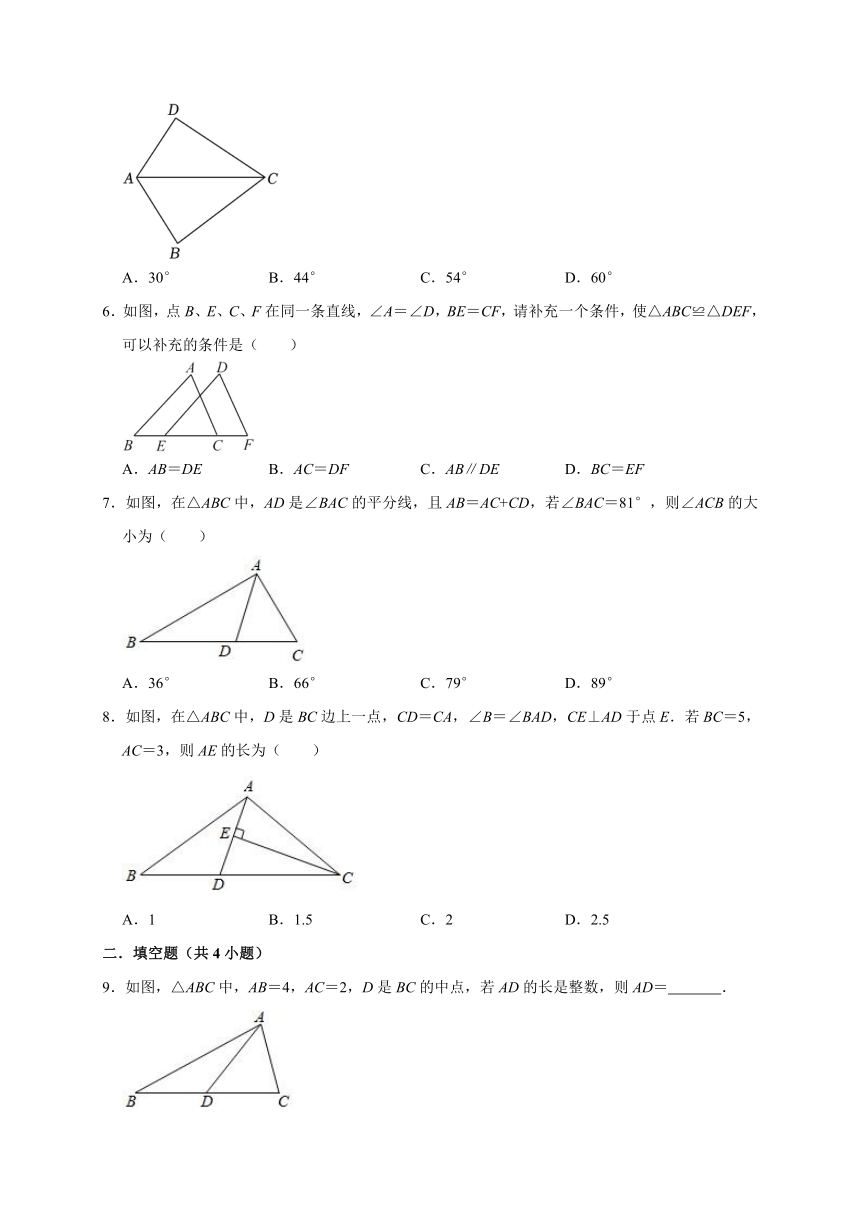
5.如图,已知∠B=96°,∠DCA=∠BCA=30°,DC=BC,则∠DAC的度数为( )
A.30° B.44° C.54° D.60°
6.如图,点B、E、C、F在同一条直线,∠A=∠D,BE=CF,请补充一个条件,使△ABC≌△DEF,可以补充的条件是( )
A.AB=DE B.AC=DF C.AB∥DE D.BC=EF
7.如图,在△ABC中,AD是∠BAC的平分线,且AB=AC+CD,若∠BAC=81°,则∠ACB的大小为( )
A.36° B.66° C.79° D.89°
8.如图,在△ABC中,D是BC边上一点,CD=CA,∠B=∠BAD,CE⊥AD于点E.若BC=5,AC=3,则AE的长为( )
A.1 B.1.5 C.2 D.2.5
二.填空题(共4小题)
9.如图,△ABC中,AB=4,AC=2,D是BC的中点,若AD的长是整数,则AD= .
10.已知△ABC与△DEF的三边对应相等,三个角也对应相等,则能判定△ABC与△DEF全等的方法有 种.
11.如图,△ABC中,∠C=90°,AC=10cm,BC=5cm,线段PQ=AB,点P、Q分别在AC和与AC垂直的射线AM上移动,当AP= 时,△ABC和△QPA全等.
12.如图,在△ABC中,AQ=PQ,PR=PS,PR⊥AB于点R,PS⊥AC于点S,则以下三个结论:①AS=AR;②QP∥AR;③△BRP≌△QSP中,正确的有 .
三.解答题(共10小题)
13.如图,AB∥DC,AB=DC,AF=DE,求证:△ABE≌△DCF.
14.如图,AD、BC相交于点O,AD=BC,∠C=∠D=90°,求证:AO=BO.
15.如图,已知△ADE≌△ACB,∠EAC=10°,∠B=25°,∠BAD=120°,求∠DAE,∠C的度数.
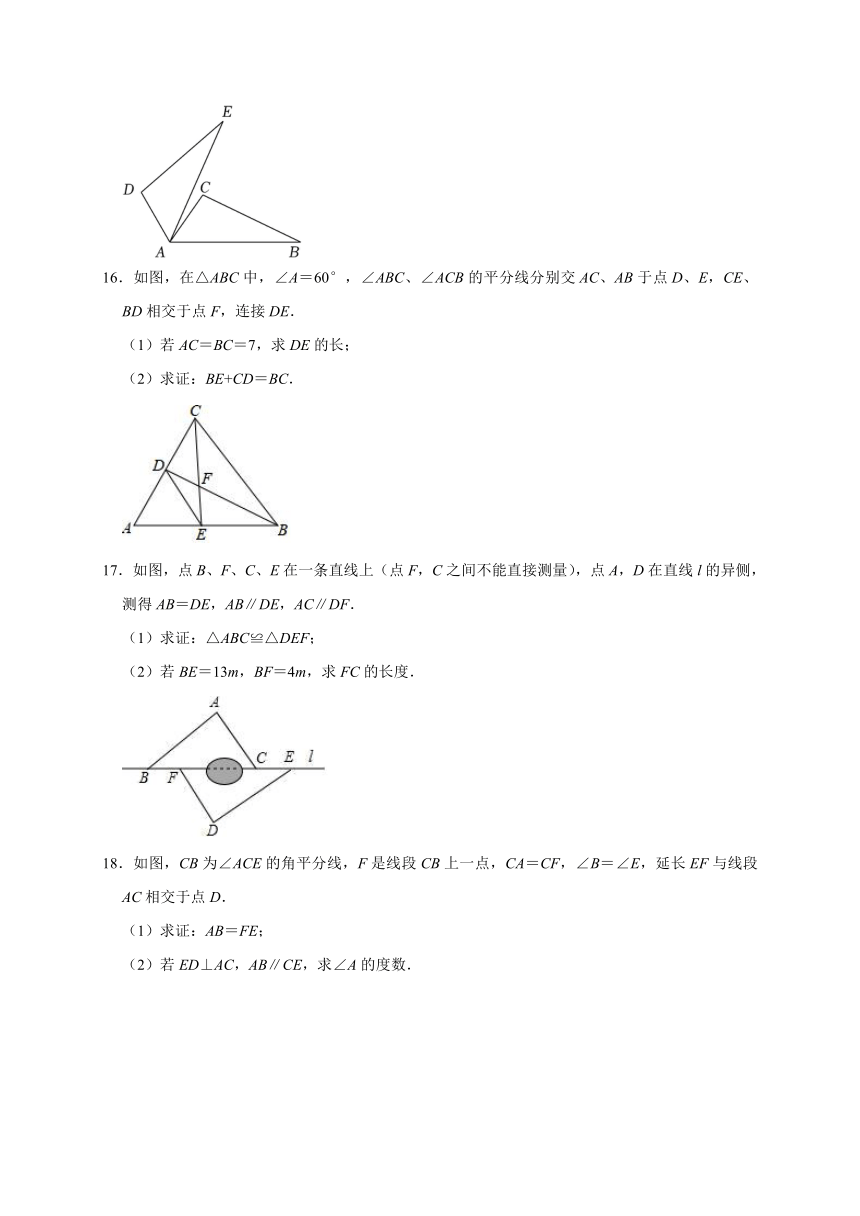
16.如图,在△ABC中,∠A=60°,∠ABC、∠ACB的平分线分别交AC、AB于点D、E,CE、BD相交于点F,连接DE.
(1)若AC=BC=7,求DE的长;
(2)求证:BE+CD=BC.
17.如图,点B、F、C、E在一条直线上(点F,C之间不能直接测量),点A,D在直线l的异侧,测得AB=DE,AB∥DE,AC∥DF.
(1)求证:△ABC≌△DEF;
(2)若BE=13m,BF=4m,求FC的长度.
18.如图,CB为∠ACE的角平分线,F是线段CB上一点,CA=CF,∠B=∠E,延长EF与线段AC相交于点D.
(1)求证:AB=FE;
(2)若ED⊥AC,AB∥CE,求∠A的度数.
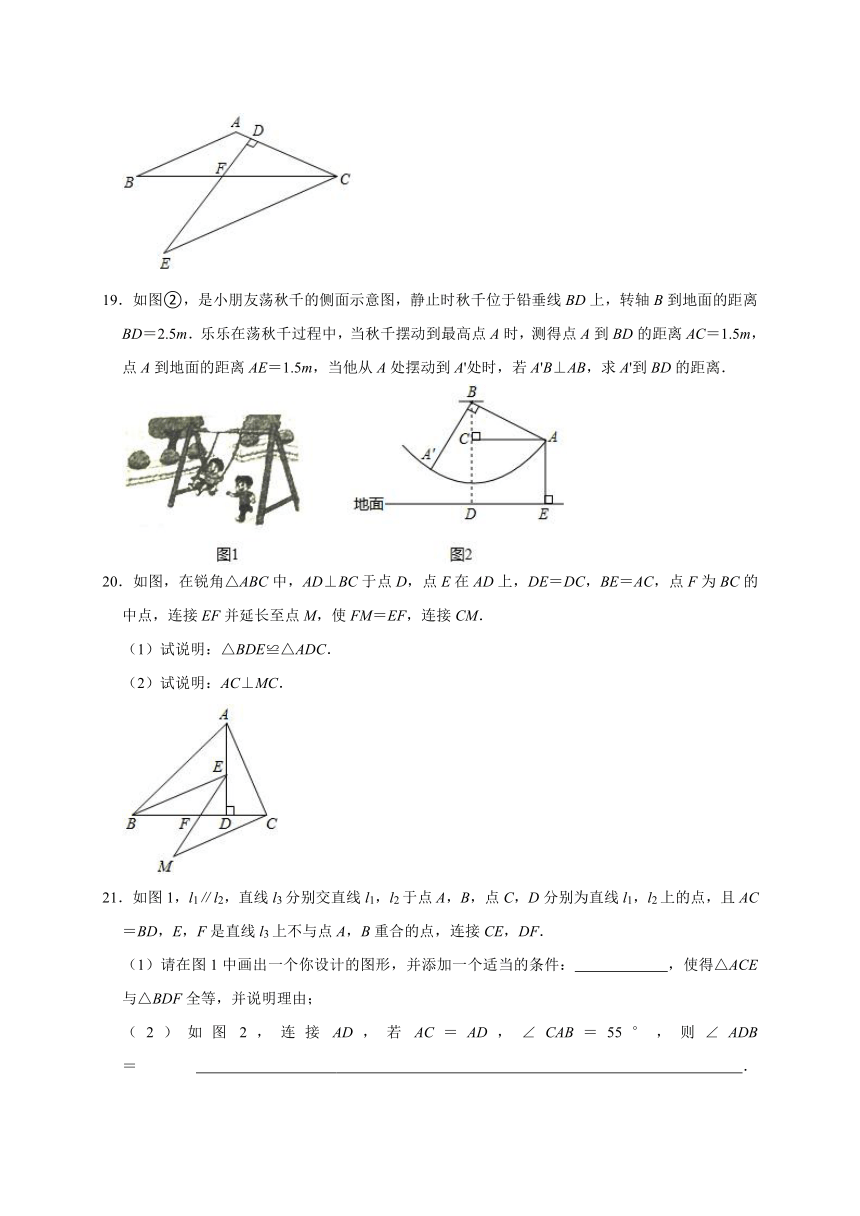
19.如图②,是小朋友荡秋千的侧面示意图,静止时秋千位于铅垂线BD上,转轴B到地面的距离BD=2.5m.乐乐在荡秋千过程中,当秋千摆动到最高点A时,测得点A到BD的距离AC=1.5m,点A到地面的距离AE=1.5m,当他从A处摆动到A'处时,若A'B⊥AB,求A'到BD的距离.
20.如图,在锐角△ABC中,AD⊥BC于点D,点E在AD上,DE=DC,BE=AC,点F为BC的中点,连接EF并延长至点M,使FM=EF,连接CM.
(1)试说明:△BDE≌△ADC.
(2)试说明:AC⊥MC.
21.如图1,l1∥l2,直线l3分别交直线l1,l2于点A,B,点C,D分别为直线l1,l2上的点,且AC=BD,E,F是直线l3上不与点A,B重合的点,连接CE,DF.
(1)请在图1中画出一个你设计的图形,并添加一个适当的条件: ,使得△ACE与△BDF全等,并说明理由;
(2)如图2,连接AD,若AC=AD,∠CAB=55°,则∠ADB= .
22.在△ABC中,AB=AC,D是△ABC外一点,连接AD,BD,CD.
(1)如图1,若∠ABC=60°,∠BDC=120°,探究∠BDA与∠CDA的关系,理由.
(2)如图2,若将(1)中的条件改为∠BAC+∠BDC=180°,(1)中的结论是否成立,理由.
13.2 三角形全等的判定(同步特训)华东师大新版八年级上学期数学
参考答案与试题解析
一.选择题(共8小题)
1.如图是两个全等三角形,图中的字母表示三角形的边长,则∠1的度数是( )
A.54° B.56° C.60° D.66°
【答案】D
【解答】解:
∵△ABC≌△DEF,
∴∠F=∠C=∠1,
∵∠A=54°,∠B=60°,
∴∠1=∠C=180°﹣∠A﹣∠B=180°﹣54°﹣60°=66°,
故选:D.
2.在△ABC中,AD平分∠BAC,∠B=2∠ADB,AB=3,CD=5,则AC的长为( )
A.6 B.7 C.8 D.9
【答案】C
【解答】解:在AC上截取AE=AB,连接DE,
∵AD平分∠BAC,
∴∠BAD=∠DAC,
在△ABD和△AED中,
,
∴△ABD≌△AED(SAS),
∴∠B=∠AED,∠ADB=∠ADE,BD=DE,又∠B=2∠ADB,
∴∠AED=2∠ADB,
而∠BDE=∠ADB+∠ADE=2∠ADB,
∴∠BDE=∠AED,
∴∠CED=∠EDC,
∴CD=CE,
∴AC=AE+CE=AB+CD=3+5=8.
故选:C.
3.如图,有一块三角形玻璃,小明不小心将它打破.带上这块玻璃,能配成同样大小的一块,其理由是( )
A.SSS B.ASA C.SAS D.HL
【答案】B
【解答】解:破玻璃保留了原来三角形的两个角和一边,则可以根据ASA来配一块一样的玻璃,
故选:B.
4.如图,点B,C,E在同一条直线上,∠B=∠E=∠ACF=60°,AB=CE,则与线段BC相等的线段是( )
A.AC B.AF C.CF D.EF
【答案】D
【解答】解:∵∠ACE=∠B+∠CAB=∠ACF+∠ECF,∠B=∠E=∠ACF=60°,
∴∠ECF=∠BAC,
∵AB=CE,
∴△ABC≌△CEF(ASA),
∴BC=EF.
故选:D.
5.如图,已知∠B=96°,∠DCA=∠BCA=30°,DC=BC,则∠DAC的度数为( )
A.30° B.44° C.54° D.60°
【答案】C
【解答】解:在△ACD和△ACB中,
,
∴△ACD≌△ACB(SAS),
∴∠D=∠B=96°,
∴∠DAC=180°﹣∠DCA﹣∠D=180°﹣30°﹣96°=54°,
故选:C.
6.如图,点B、E、C、F在同一条直线,∠A=∠D,BE=CF,请补充一个条件,使△ABC≌△DEF,可以补充的条件是( )
A.AB=DE B.AC=DF C.AB∥DE D.BC=EF
【答案】C
【解答】解:∵BE=CF,
∴BE+CE=CF+CE,
即BC=EF,
A.AB=DE,BC=EF,∠A=∠D不符合全等三角形的判定定理,不能推出△ABC≌△DEF,故本选项不符合题意;
B.AC=DF,BC=EF,∠A=∠D不符合全等三角形的判定定理,不能推出△ABC≌△DEF,故本选项不符合题意;
C.∵AB∥DE,
∴∠B=∠DEF,
条件∠B=∠DEF,∠A=∠D,BC=EF符合全等三角形的判定定理,能推出△ABC≌△DEF,故本选项符合题意;
D.BC=EF,∠A=∠D不符合全等三角形的判定定理,不能推出△ABC≌△DEF,故本选项不符合题意;
故选:C.
7.如图,在△ABC中,AD是∠BAC的平分线,且AB=AC+CD,若∠BAC=81°,则∠ACB的大小为( )
A.36° B.66° C.79° D.89°
【答案】B
【解答】解:在AB上截取AC'=AC,连接DC',
∵AB=AC+CD,
∴BC'=DC,
∵AD是∠BAC的角平分线,
∴∠C'AD=∠DAC,
在△ACD和△AC'D中,
,
∴△ACD≌△AC'D(SAS),
∴C'D=CD,∠ACD=∠AC'D,
∴DC'=BC',
∴△BC'D是等腰三角形,
∴∠C'BD=∠C'DB,
设∠C'BD=∠C'DB=x,则∠ACD=∠AC'D=2x,
∵∠BAC=81°,
∴x+2x+81°=180°,
解得:x=33°,
∴∠ACB=33°×2=66°,
故选:B.
8.如图,在△ABC中,D是BC边上一点,CD=CA,∠B=∠BAD,CE⊥AD于点E.若BC=5,AC=3,则AE的长为( )
A.1 B.1.5 C.2 D.2.5
【答案】A
【解答】解:∵CE⊥AD于点E,
∴∠CEA=∠CED=90°,
在Rt△CEA和Rt△CED中,
,
∴Rt△CEA≌Rt△CED(HL),
∴AE=DE,
∵BC=5,AC=3,
∴BD=BC﹣CD=BC﹣AC=5﹣3=2,
∵∠B=∠BAD,
∴BD=AD=2,
∴AE=AD=1.
故选:A.
二.填空题(共4小题)
9.如图,△ABC中,AB=4,AC=2,D是BC的中点,若AD的长是整数,则AD= 2 .
【答案】2.
【解答】解:如图,AB=4,AC=2,AD是BC上的中线,
延长AD到E,使DE=AD,连接BE,
在△ADC和△EDB中,
,
∴△ADC≌△EDB(SAS),
∴BE=AC=2,
在△ABE中,BE﹣AB<AE<AB+BE,
即2<2AD<6,
解得1<AD<3,
又∵AD是整数,
∴AD=2,
故答案为:2.
10.已知△ABC与△DEF的三边对应相等,三个角也对应相等,则能判定△ABC与△DEF全等的方法有 4 种.
【答案】4.
【解答】解:根据全等三角形的判定方法,存在判定方法SSS、SAS、ASA、AAS,共4种.
故答案为:4.
11.如图,△ABC中,∠C=90°,AC=10cm,BC=5cm,线段PQ=AB,点P、Q分别在AC和与AC垂直的射线AM上移动,当AP= 5cm或10cm 时,△ABC和△QPA全等.
【答案】5cm或10cm.
【解答】解:∵PQ=AB,
∴根据三角形全等的判定方法HL可知,
①当P运动到AP=BC时,△ABC≌△QPA,即AP=BC=5cm;
②当P运动到与C点重合时,△QAP≌△BCA,即AP=AC=10cm.
故答案为:5cm或10cm.
12.如图,在△ABC中,AQ=PQ,PR=PS,PR⊥AB于点R,PS⊥AC于点S,则以下三个结论:①AS=AR;②QP∥AR;③△BRP≌△QSP中,正确的有 ①② .
【答案】①②.
【解答】解:∵PR⊥AB于R,PS⊥AC于S,
∴∠ARP=∠ASP=90°,
在Rt△APR和Rt△APS中,
,
∴Rt△APR≌Rt△APS(HL),
∴AS=AR,∠1=∠2,故①正确,
∵AQ=PQ,
∴∠2=∠3,
∴∠1=∠3,
∴PQ∥AR,故②正确,
在△BRP和△CSP中,只有一个角,一条边相等无法证明全等.故③错误,
故答案为:①②.
三.解答题(共10小题)
13.如图,AB∥DC,AB=DC,AF=DE,求证:△ABE≌△DCF.
【答案】见试题解答内容
【解答】证明:∵AB∥DC,
∴∠D=∠A,
又AF=DE,
∴AF+FE=DE+EF,
即 AE=DF,
在△CDF和△BAE中,
∴△ABE≌△DCF(SAS)
14.如图,AD、BC相交于点O,AD=BC,∠C=∠D=90°,求证:AO=BO.
【答案】证明过程见解析.
【解答】证明:在Rt△ABC与Rt△BAD中,
,
∴Rt△ABC≌Rt△BAD(HL),
∴∠ABC=∠BAD,
∴AO=BO.
15.如图,已知△ADE≌△ACB,∠EAC=10°,∠B=25°,∠BAD=120°,求∠DAE,∠C的度数.
【答案】∠DAE=55°;∠C=100°.
【解答】解:∵∠EAC=10°,∠BAD=120°,
∴∠DAE+∠CAB=∠BAD﹣∠EAC=110°.
∵△ADE≌△ACB,
∴∠DAE=∠CAB=110°÷2=55°,
∴∠C=180°﹣∠B﹣∠CAB=100°.
16.如图,在△ABC中,∠A=60°,∠ABC、∠ACB的平分线分别交AC、AB于点D、E,CE、BD相交于点F,连接DE.
(1)若AC=BC=7,求DE的长;
(2)求证:BE+CD=BC.
【答案】(1);
(2)证明过程见解析.
【解答】解:(1)∵AC=BC,∠A=60°,
∴△ABC为等边三角形,
∴AC=AB,
又∵BD、CE分别是∠ABC、∠ACB的平分线,
∴D、E分别是AC、AB的中点,
∴AD=AC,AE=AB,
∴AD=AE,
∴△ADE为等边三角形,
∴DE=AE=;
(2)证明:在BC上截取BH=BE,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵BF=BF
∴△EBF≌△HBF(SAS),
∴∠EFB=∠HFB=60°.
∵∠A=60°,
∴∠ABC+∠ACB=120°,
∵BD平分∠ABC,CE平分∠ACB,
∴∠ABD=∠CBD,∠ACE=∠BCE,
∴∠CBD+∠BCE=60°,
∴∠BFE=60°,
∴∠CFB=120°,
∴∠CFH=60°,
∴∠CFH=∠CFD=60°,
∵CF=CF,
∴△CDF≌△CHF(ASA).
∴CD=CH,
∵CH+BH=BC,
∴BE+CD=BC.
17.如图,点B、F、C、E在一条直线上(点F,C之间不能直接测量),点A,D在直线l的异侧,测得AB=DE,AB∥DE,AC∥DF.
(1)求证:△ABC≌△DEF;
(2)若BE=13m,BF=4m,求FC的长度.
【答案】见试题解答内容
【解答】(1)证明:∵AB∥DE,
∴∠ABC=∠DEF,
∴AC∥DF,
∴∠ACB=∠DFE,
在△ABC与△DEF中,
,
∴△ABC≌△DEF(AAS);
(2)解:∵△ABC≌△DEF,
∴BC=EF,
∴BF+FC=EC+FC,
∴BF=EC,
∵BE=13m,BF=4m,
∴FC=13﹣4﹣4=5m.
18.如图,CB为∠ACE的角平分线,F是线段CB上一点,CA=CF,∠B=∠E,延长EF与线段AC相交于点D.
(1)求证:AB=FE;
(2)若ED⊥AC,AB∥CE,求∠A的度数.
【答案】(1)证明见解析;
(2)120°.
【解答】(1)证明:∵CB为∠ACE的角平分线,
∴∠ACB=∠BCE,
在△ACB和△FCE中,
,
∴△ACB≌△FCE(AAS),
∴AB=FE;
(2)解:∵AB∥CE,
∴∠ABC=∠BCE,
∵∠BCE=∠ACB,
∴∠ABC=∠ACB,
∴AB=AC,
∵△ACB≌△FCE,
∴FE=FC,
∴∠E=∠FCE,
设∠FCE=x,
则∠E=x,∠ACB=x,
∵ED⊥AC,
∴∠EDC=90°,
∴3x+90°=180°,
解得x=30°,
∴∠ACB=∠ABC=30°,
∴∠A=120°.
19.如图②,是小朋友荡秋千的侧面示意图,静止时秋千位于铅垂线BD上,转轴B到地面的距离BD=2.5m.乐乐在荡秋千过程中,当秋千摆动到最高点A时,测得点A到BD的距离AC=1.5m,点A到地面的距离AE=1.5m,当他从A处摆动到A'处时,若A'B⊥AB,求A'到BD的距离.
【答案】A'到BD的距离是1m.
【解答】解:如图2,作A'F⊥BD,垂足为F.
∵AC⊥BD,
∴∠ACB=∠A'FB=90°;
在Rt△A'FB中,∠1+∠3=90°;
又∵A'B⊥AB,
∴∠1+∠2=90°,
∴∠2=∠3;
在△ACB和△BFA'中,
,
∴△ACB≌△BFA'(AAS);
∴A'F=BC
∵AC∥DE且CD⊥AC,AE⊥DE,
∴CD=AE=1.5m;
∴BC=BD﹣CD=2.5﹣1.5=1(m),
∴A'F=1(m),
即A'到BD的距离是1m.
20.如图,在锐角△ABC中,AD⊥BC于点D,点E在AD上,DE=DC,BE=AC,点F为BC的中点,连接EF并延长至点M,使FM=EF,连接CM.
(1)试说明:△BDE≌△ADC.
(2)试说明:AC⊥MC.
【答案】(1)见解析过程;
(2)见解析过程.
【解答】解:(1)∵AD⊥BC,
∴∠BDE=∠ADC=90°,
在Rt△BDE与Rt△ADC中,
,
∴Rt△BDE≌Rt△ADC(HL),
(2)∵F为BC中点,
∴BF=CF,
在△BFE与△CFM中,
,
∴△BFE≌△CFM(SAS),
∴∠CBE=∠BCM,BE=MC,
∵Rt△BDE≌Rt△ADC,
∴∠CBE=∠CAD,
∴∠CAD=∠BCM,
∵∠CAD+∠ACD=90°,
∴∠BCM+∠ACD=90°,
即∠ACM=90°,
∴AC⊥MC.
21.如图1,l1∥l2,直线l3分别交直线l1,l2于点A,B,点C,D分别为直线l1,l2上的点,且AC=BD,E,F是直线l3上不与点A,B重合的点,连接CE,DF.
(1)请在图1中画出一个你设计的图形,并添加一个适当的条件: AE=BF ,使得△ACE与△BDF全等,并说明理由;
(2)如图2,连接AD,若AC=AD,∠CAB=55°,则∠ADB= 70° .
【答案】(1)AE=BF,
理由见解析;
(2)70°.
【解答】解:(1)添加一个适当的条件:AE=BF,
理由:如图1,
∵l1∥l2,
∴∠CAE=∠DBF,
在△ACE与△BDF中,
,
∴△ACE≌△BDF(SAS);
故答案为:AE=BF;
(2)如图2,连接BC,
∵l1∥l2,
即AC∥BD,
∵AC=BD,
∴四边形ACBD是平行四边形,
∵AC=AD,
∴四边形ACBD是菱形,
∴∠DAB=∠CAB=∠ABD=55°,
∴∠ADB=180°﹣55°﹣55°=70°.
解法2:∵l1∥l2,
∴∠CAB=∠ABD,∠CAD+∠BDA=180°,
∵AC=BD,AC=AD,
∴BD=AD,
∴∠DAB=∠ABD,
∵∠CAB=55°,
∴∠ABD=∠BAD=55°,
∴∠CAD=110°,
∴∠ADB=180°﹣110°=70°,
故答案为:70°.
22.在△ABC中,AB=AC,D是△ABC外一点,连接AD,BD,CD.
(1)如图1,若∠ABC=60°,∠BDC=120°,探究∠BDA与∠CDA的关系,理由.
(2)如图2,若将(1)中的条件改为∠BAC+∠BDC=180°,(1)中的结论是否成立,理由.
【答案】(1)∠BDA=∠CDA;
(2)结论仍成立.
【解答】解:(1)∠BDA=∠CDA,
理由是:∵在△ABC中,AB=AC,∠ABC=60°,
∴∠ACB=∠ABC=60°,
∴∠BAC=180°﹣60°﹣60°=60°,
过A作AE⊥BD于E,AF⊥DC于F,
∵AE⊥BD,AF⊥DC,
∴∠AED=∠F=90°,
∵∠BDC=120°,
∴∠EAF=360°﹣90°﹣90°﹣120°=60°=∠BAC,
即∠EAF﹣∠EAC=∠BAC﹣∠EAC,
∴∠BAE=∠CAF,
在△BAE和△CAF中
,
∴△BAE≌△CAF(AAS),
∴AE=AF,
在Rt△ADE和Rt△ADF中
,
∴Rt△ADE≌Rt△ADF(HL),
∴∠BDA=∠CDA.
(2)结论还成立,
理由是:过A作AE⊥BD于E,AF⊥DC于F,
∵AE⊥BD,AF⊥DC,
∴∠AED=∠F=90°,
∵∠BDC=120°,
∴∠EAF+∠BDC=180°,
∵∠BAC+∠BDC=180°,
∴∠EAF=∠BAC,
∴∠EAF﹣∠EAC=∠BAC﹣∠EAC,
∴∠BAE=∠CAF,
在△BAE和△CAF中
,
∴△BAE≌△CAF(AAS),
∴AE=AF,
在Rt△ADE和Rt△ADF中
,
∴Rt△ADE≌Rt△ADF(HL),
∴∠BDA=∠CDA,
即结论仍成立.
华东师大新版八年级上学期数学
一.选择题(共8小题)
1.如图是两个全等三角形,图中的字母表示三角形的边长,则∠1的度数是( )
A.54° B.56° C.60° D.66°
2.在△ABC中,AD平分∠BAC,∠B=2∠ADB,AB=3,CD=5,则AC的长为( )
A.6 B.7 C.8 D.9
3.如图,有一块三角形玻璃,小明不小心将它打破.带上这块玻璃,能配成同样大小的一块,其理由是( )
A.SSS B.ASA C.SAS D.HL
4.如图,点B,C,E在同一条直线上,∠B=∠E=∠ACF=60°,AB=CE,则与线段BC相等的线段是( )
A.AC B.AF C.CF D.EF
5.如图,已知∠B=96°,∠DCA=∠BCA=30°,DC=BC,则∠DAC的度数为( )
A.30° B.44° C.54° D.60°
6.如图,点B、E、C、F在同一条直线,∠A=∠D,BE=CF,请补充一个条件,使△ABC≌△DEF,可以补充的条件是( )
A.AB=DE B.AC=DF C.AB∥DE D.BC=EF
7.如图,在△ABC中,AD是∠BAC的平分线,且AB=AC+CD,若∠BAC=81°,则∠ACB的大小为( )
A.36° B.66° C.79° D.89°
8.如图,在△ABC中,D是BC边上一点,CD=CA,∠B=∠BAD,CE⊥AD于点E.若BC=5,AC=3,则AE的长为( )
A.1 B.1.5 C.2 D.2.5
二.填空题(共4小题)
9.如图,△ABC中,AB=4,AC=2,D是BC的中点,若AD的长是整数,则AD= .
10.已知△ABC与△DEF的三边对应相等,三个角也对应相等,则能判定△ABC与△DEF全等的方法有 种.
11.如图,△ABC中,∠C=90°,AC=10cm,BC=5cm,线段PQ=AB,点P、Q分别在AC和与AC垂直的射线AM上移动,当AP= 时,△ABC和△QPA全等.
12.如图,在△ABC中,AQ=PQ,PR=PS,PR⊥AB于点R,PS⊥AC于点S,则以下三个结论:①AS=AR;②QP∥AR;③△BRP≌△QSP中,正确的有 .
三.解答题(共10小题)
13.如图,AB∥DC,AB=DC,AF=DE,求证:△ABE≌△DCF.
14.如图,AD、BC相交于点O,AD=BC,∠C=∠D=90°,求证:AO=BO.
15.如图,已知△ADE≌△ACB,∠EAC=10°,∠B=25°,∠BAD=120°,求∠DAE,∠C的度数.
16.如图,在△ABC中,∠A=60°,∠ABC、∠ACB的平分线分别交AC、AB于点D、E,CE、BD相交于点F,连接DE.
(1)若AC=BC=7,求DE的长;
(2)求证:BE+CD=BC.
17.如图,点B、F、C、E在一条直线上(点F,C之间不能直接测量),点A,D在直线l的异侧,测得AB=DE,AB∥DE,AC∥DF.
(1)求证:△ABC≌△DEF;
(2)若BE=13m,BF=4m,求FC的长度.
18.如图,CB为∠ACE的角平分线,F是线段CB上一点,CA=CF,∠B=∠E,延长EF与线段AC相交于点D.
(1)求证:AB=FE;
(2)若ED⊥AC,AB∥CE,求∠A的度数.
19.如图②,是小朋友荡秋千的侧面示意图,静止时秋千位于铅垂线BD上,转轴B到地面的距离BD=2.5m.乐乐在荡秋千过程中,当秋千摆动到最高点A时,测得点A到BD的距离AC=1.5m,点A到地面的距离AE=1.5m,当他从A处摆动到A'处时,若A'B⊥AB,求A'到BD的距离.
20.如图,在锐角△ABC中,AD⊥BC于点D,点E在AD上,DE=DC,BE=AC,点F为BC的中点,连接EF并延长至点M,使FM=EF,连接CM.
(1)试说明:△BDE≌△ADC.
(2)试说明:AC⊥MC.
21.如图1,l1∥l2,直线l3分别交直线l1,l2于点A,B,点C,D分别为直线l1,l2上的点,且AC=BD,E,F是直线l3上不与点A,B重合的点,连接CE,DF.
(1)请在图1中画出一个你设计的图形,并添加一个适当的条件: ,使得△ACE与△BDF全等,并说明理由;
(2)如图2,连接AD,若AC=AD,∠CAB=55°,则∠ADB= .
22.在△ABC中,AB=AC,D是△ABC外一点,连接AD,BD,CD.
(1)如图1,若∠ABC=60°,∠BDC=120°,探究∠BDA与∠CDA的关系,理由.
(2)如图2,若将(1)中的条件改为∠BAC+∠BDC=180°,(1)中的结论是否成立,理由.
13.2 三角形全等的判定(同步特训)华东师大新版八年级上学期数学
参考答案与试题解析
一.选择题(共8小题)
1.如图是两个全等三角形,图中的字母表示三角形的边长,则∠1的度数是( )
A.54° B.56° C.60° D.66°
【答案】D
【解答】解:
∵△ABC≌△DEF,
∴∠F=∠C=∠1,
∵∠A=54°,∠B=60°,
∴∠1=∠C=180°﹣∠A﹣∠B=180°﹣54°﹣60°=66°,
故选:D.
2.在△ABC中,AD平分∠BAC,∠B=2∠ADB,AB=3,CD=5,则AC的长为( )
A.6 B.7 C.8 D.9
【答案】C
【解答】解:在AC上截取AE=AB,连接DE,
∵AD平分∠BAC,
∴∠BAD=∠DAC,
在△ABD和△AED中,
,
∴△ABD≌△AED(SAS),
∴∠B=∠AED,∠ADB=∠ADE,BD=DE,又∠B=2∠ADB,
∴∠AED=2∠ADB,
而∠BDE=∠ADB+∠ADE=2∠ADB,
∴∠BDE=∠AED,
∴∠CED=∠EDC,
∴CD=CE,
∴AC=AE+CE=AB+CD=3+5=8.
故选:C.
3.如图,有一块三角形玻璃,小明不小心将它打破.带上这块玻璃,能配成同样大小的一块,其理由是( )
A.SSS B.ASA C.SAS D.HL
【答案】B
【解答】解:破玻璃保留了原来三角形的两个角和一边,则可以根据ASA来配一块一样的玻璃,
故选:B.
4.如图,点B,C,E在同一条直线上,∠B=∠E=∠ACF=60°,AB=CE,则与线段BC相等的线段是( )
A.AC B.AF C.CF D.EF
【答案】D
【解答】解:∵∠ACE=∠B+∠CAB=∠ACF+∠ECF,∠B=∠E=∠ACF=60°,
∴∠ECF=∠BAC,
∵AB=CE,
∴△ABC≌△CEF(ASA),
∴BC=EF.
故选:D.
5.如图,已知∠B=96°,∠DCA=∠BCA=30°,DC=BC,则∠DAC的度数为( )
A.30° B.44° C.54° D.60°
【答案】C
【解答】解:在△ACD和△ACB中,
,
∴△ACD≌△ACB(SAS),
∴∠D=∠B=96°,
∴∠DAC=180°﹣∠DCA﹣∠D=180°﹣30°﹣96°=54°,
故选:C.
6.如图,点B、E、C、F在同一条直线,∠A=∠D,BE=CF,请补充一个条件,使△ABC≌△DEF,可以补充的条件是( )
A.AB=DE B.AC=DF C.AB∥DE D.BC=EF
【答案】C
【解答】解:∵BE=CF,
∴BE+CE=CF+CE,
即BC=EF,
A.AB=DE,BC=EF,∠A=∠D不符合全等三角形的判定定理,不能推出△ABC≌△DEF,故本选项不符合题意;
B.AC=DF,BC=EF,∠A=∠D不符合全等三角形的判定定理,不能推出△ABC≌△DEF,故本选项不符合题意;
C.∵AB∥DE,
∴∠B=∠DEF,
条件∠B=∠DEF,∠A=∠D,BC=EF符合全等三角形的判定定理,能推出△ABC≌△DEF,故本选项符合题意;
D.BC=EF,∠A=∠D不符合全等三角形的判定定理,不能推出△ABC≌△DEF,故本选项不符合题意;
故选:C.
7.如图,在△ABC中,AD是∠BAC的平分线,且AB=AC+CD,若∠BAC=81°,则∠ACB的大小为( )
A.36° B.66° C.79° D.89°
【答案】B
【解答】解:在AB上截取AC'=AC,连接DC',
∵AB=AC+CD,
∴BC'=DC,
∵AD是∠BAC的角平分线,
∴∠C'AD=∠DAC,
在△ACD和△AC'D中,
,
∴△ACD≌△AC'D(SAS),
∴C'D=CD,∠ACD=∠AC'D,
∴DC'=BC',
∴△BC'D是等腰三角形,
∴∠C'BD=∠C'DB,
设∠C'BD=∠C'DB=x,则∠ACD=∠AC'D=2x,
∵∠BAC=81°,
∴x+2x+81°=180°,
解得:x=33°,
∴∠ACB=33°×2=66°,
故选:B.
8.如图,在△ABC中,D是BC边上一点,CD=CA,∠B=∠BAD,CE⊥AD于点E.若BC=5,AC=3,则AE的长为( )
A.1 B.1.5 C.2 D.2.5
【答案】A
【解答】解:∵CE⊥AD于点E,
∴∠CEA=∠CED=90°,
在Rt△CEA和Rt△CED中,
,
∴Rt△CEA≌Rt△CED(HL),
∴AE=DE,
∵BC=5,AC=3,
∴BD=BC﹣CD=BC﹣AC=5﹣3=2,
∵∠B=∠BAD,
∴BD=AD=2,
∴AE=AD=1.
故选:A.
二.填空题(共4小题)
9.如图,△ABC中,AB=4,AC=2,D是BC的中点,若AD的长是整数,则AD= 2 .
【答案】2.
【解答】解:如图,AB=4,AC=2,AD是BC上的中线,
延长AD到E,使DE=AD,连接BE,
在△ADC和△EDB中,
,
∴△ADC≌△EDB(SAS),
∴BE=AC=2,
在△ABE中,BE﹣AB<AE<AB+BE,
即2<2AD<6,
解得1<AD<3,
又∵AD是整数,
∴AD=2,
故答案为:2.
10.已知△ABC与△DEF的三边对应相等,三个角也对应相等,则能判定△ABC与△DEF全等的方法有 4 种.
【答案】4.
【解答】解:根据全等三角形的判定方法,存在判定方法SSS、SAS、ASA、AAS,共4种.
故答案为:4.
11.如图,△ABC中,∠C=90°,AC=10cm,BC=5cm,线段PQ=AB,点P、Q分别在AC和与AC垂直的射线AM上移动,当AP= 5cm或10cm 时,△ABC和△QPA全等.
【答案】5cm或10cm.
【解答】解:∵PQ=AB,
∴根据三角形全等的判定方法HL可知,
①当P运动到AP=BC时,△ABC≌△QPA,即AP=BC=5cm;
②当P运动到与C点重合时,△QAP≌△BCA,即AP=AC=10cm.
故答案为:5cm或10cm.
12.如图,在△ABC中,AQ=PQ,PR=PS,PR⊥AB于点R,PS⊥AC于点S,则以下三个结论:①AS=AR;②QP∥AR;③△BRP≌△QSP中,正确的有 ①② .
【答案】①②.
【解答】解:∵PR⊥AB于R,PS⊥AC于S,
∴∠ARP=∠ASP=90°,
在Rt△APR和Rt△APS中,
,
∴Rt△APR≌Rt△APS(HL),
∴AS=AR,∠1=∠2,故①正确,
∵AQ=PQ,
∴∠2=∠3,
∴∠1=∠3,
∴PQ∥AR,故②正确,
在△BRP和△CSP中,只有一个角,一条边相等无法证明全等.故③错误,
故答案为:①②.
三.解答题(共10小题)
13.如图,AB∥DC,AB=DC,AF=DE,求证:△ABE≌△DCF.
【答案】见试题解答内容
【解答】证明:∵AB∥DC,
∴∠D=∠A,
又AF=DE,
∴AF+FE=DE+EF,
即 AE=DF,
在△CDF和△BAE中,
∴△ABE≌△DCF(SAS)
14.如图,AD、BC相交于点O,AD=BC,∠C=∠D=90°,求证:AO=BO.
【答案】证明过程见解析.
【解答】证明:在Rt△ABC与Rt△BAD中,
,
∴Rt△ABC≌Rt△BAD(HL),
∴∠ABC=∠BAD,
∴AO=BO.
15.如图,已知△ADE≌△ACB,∠EAC=10°,∠B=25°,∠BAD=120°,求∠DAE,∠C的度数.
【答案】∠DAE=55°;∠C=100°.
【解答】解:∵∠EAC=10°,∠BAD=120°,
∴∠DAE+∠CAB=∠BAD﹣∠EAC=110°.
∵△ADE≌△ACB,
∴∠DAE=∠CAB=110°÷2=55°,
∴∠C=180°﹣∠B﹣∠CAB=100°.
16.如图,在△ABC中,∠A=60°,∠ABC、∠ACB的平分线分别交AC、AB于点D、E,CE、BD相交于点F,连接DE.
(1)若AC=BC=7,求DE的长;
(2)求证:BE+CD=BC.
【答案】(1);
(2)证明过程见解析.
【解答】解:(1)∵AC=BC,∠A=60°,
∴△ABC为等边三角形,
∴AC=AB,
又∵BD、CE分别是∠ABC、∠ACB的平分线,
∴D、E分别是AC、AB的中点,
∴AD=AC,AE=AB,
∴AD=AE,
∴△ADE为等边三角形,
∴DE=AE=;
(2)证明:在BC上截取BH=BE,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵BF=BF
∴△EBF≌△HBF(SAS),
∴∠EFB=∠HFB=60°.
∵∠A=60°,
∴∠ABC+∠ACB=120°,
∵BD平分∠ABC,CE平分∠ACB,
∴∠ABD=∠CBD,∠ACE=∠BCE,
∴∠CBD+∠BCE=60°,
∴∠BFE=60°,
∴∠CFB=120°,
∴∠CFH=60°,
∴∠CFH=∠CFD=60°,
∵CF=CF,
∴△CDF≌△CHF(ASA).
∴CD=CH,
∵CH+BH=BC,
∴BE+CD=BC.
17.如图,点B、F、C、E在一条直线上(点F,C之间不能直接测量),点A,D在直线l的异侧,测得AB=DE,AB∥DE,AC∥DF.
(1)求证:△ABC≌△DEF;
(2)若BE=13m,BF=4m,求FC的长度.
【答案】见试题解答内容
【解答】(1)证明:∵AB∥DE,
∴∠ABC=∠DEF,
∴AC∥DF,
∴∠ACB=∠DFE,
在△ABC与△DEF中,
,
∴△ABC≌△DEF(AAS);
(2)解:∵△ABC≌△DEF,
∴BC=EF,
∴BF+FC=EC+FC,
∴BF=EC,
∵BE=13m,BF=4m,
∴FC=13﹣4﹣4=5m.
18.如图,CB为∠ACE的角平分线,F是线段CB上一点,CA=CF,∠B=∠E,延长EF与线段AC相交于点D.
(1)求证:AB=FE;
(2)若ED⊥AC,AB∥CE,求∠A的度数.
【答案】(1)证明见解析;
(2)120°.
【解答】(1)证明:∵CB为∠ACE的角平分线,
∴∠ACB=∠BCE,
在△ACB和△FCE中,
,
∴△ACB≌△FCE(AAS),
∴AB=FE;
(2)解:∵AB∥CE,
∴∠ABC=∠BCE,
∵∠BCE=∠ACB,
∴∠ABC=∠ACB,
∴AB=AC,
∵△ACB≌△FCE,
∴FE=FC,
∴∠E=∠FCE,
设∠FCE=x,
则∠E=x,∠ACB=x,
∵ED⊥AC,
∴∠EDC=90°,
∴3x+90°=180°,
解得x=30°,
∴∠ACB=∠ABC=30°,
∴∠A=120°.
19.如图②,是小朋友荡秋千的侧面示意图,静止时秋千位于铅垂线BD上,转轴B到地面的距离BD=2.5m.乐乐在荡秋千过程中,当秋千摆动到最高点A时,测得点A到BD的距离AC=1.5m,点A到地面的距离AE=1.5m,当他从A处摆动到A'处时,若A'B⊥AB,求A'到BD的距离.
【答案】A'到BD的距离是1m.
【解答】解:如图2,作A'F⊥BD,垂足为F.
∵AC⊥BD,
∴∠ACB=∠A'FB=90°;
在Rt△A'FB中,∠1+∠3=90°;
又∵A'B⊥AB,
∴∠1+∠2=90°,
∴∠2=∠3;
在△ACB和△BFA'中,
,
∴△ACB≌△BFA'(AAS);
∴A'F=BC
∵AC∥DE且CD⊥AC,AE⊥DE,
∴CD=AE=1.5m;
∴BC=BD﹣CD=2.5﹣1.5=1(m),
∴A'F=1(m),
即A'到BD的距离是1m.
20.如图,在锐角△ABC中,AD⊥BC于点D,点E在AD上,DE=DC,BE=AC,点F为BC的中点,连接EF并延长至点M,使FM=EF,连接CM.
(1)试说明:△BDE≌△ADC.
(2)试说明:AC⊥MC.
【答案】(1)见解析过程;
(2)见解析过程.
【解答】解:(1)∵AD⊥BC,
∴∠BDE=∠ADC=90°,
在Rt△BDE与Rt△ADC中,
,
∴Rt△BDE≌Rt△ADC(HL),
(2)∵F为BC中点,
∴BF=CF,
在△BFE与△CFM中,
,
∴△BFE≌△CFM(SAS),
∴∠CBE=∠BCM,BE=MC,
∵Rt△BDE≌Rt△ADC,
∴∠CBE=∠CAD,
∴∠CAD=∠BCM,
∵∠CAD+∠ACD=90°,
∴∠BCM+∠ACD=90°,
即∠ACM=90°,
∴AC⊥MC.
21.如图1,l1∥l2,直线l3分别交直线l1,l2于点A,B,点C,D分别为直线l1,l2上的点,且AC=BD,E,F是直线l3上不与点A,B重合的点,连接CE,DF.
(1)请在图1中画出一个你设计的图形,并添加一个适当的条件: AE=BF ,使得△ACE与△BDF全等,并说明理由;
(2)如图2,连接AD,若AC=AD,∠CAB=55°,则∠ADB= 70° .
【答案】(1)AE=BF,
理由见解析;
(2)70°.
【解答】解:(1)添加一个适当的条件:AE=BF,
理由:如图1,
∵l1∥l2,
∴∠CAE=∠DBF,
在△ACE与△BDF中,
,
∴△ACE≌△BDF(SAS);
故答案为:AE=BF;
(2)如图2,连接BC,
∵l1∥l2,
即AC∥BD,
∵AC=BD,
∴四边形ACBD是平行四边形,
∵AC=AD,
∴四边形ACBD是菱形,
∴∠DAB=∠CAB=∠ABD=55°,
∴∠ADB=180°﹣55°﹣55°=70°.
解法2:∵l1∥l2,
∴∠CAB=∠ABD,∠CAD+∠BDA=180°,
∵AC=BD,AC=AD,
∴BD=AD,
∴∠DAB=∠ABD,
∵∠CAB=55°,
∴∠ABD=∠BAD=55°,
∴∠CAD=110°,
∴∠ADB=180°﹣110°=70°,
故答案为:70°.
22.在△ABC中,AB=AC,D是△ABC外一点,连接AD,BD,CD.
(1)如图1,若∠ABC=60°,∠BDC=120°,探究∠BDA与∠CDA的关系,理由.
(2)如图2,若将(1)中的条件改为∠BAC+∠BDC=180°,(1)中的结论是否成立,理由.
【答案】(1)∠BDA=∠CDA;
(2)结论仍成立.
【解答】解:(1)∠BDA=∠CDA,
理由是:∵在△ABC中,AB=AC,∠ABC=60°,
∴∠ACB=∠ABC=60°,
∴∠BAC=180°﹣60°﹣60°=60°,
过A作AE⊥BD于E,AF⊥DC于F,
∵AE⊥BD,AF⊥DC,
∴∠AED=∠F=90°,
∵∠BDC=120°,
∴∠EAF=360°﹣90°﹣90°﹣120°=60°=∠BAC,
即∠EAF﹣∠EAC=∠BAC﹣∠EAC,
∴∠BAE=∠CAF,
在△BAE和△CAF中
,
∴△BAE≌△CAF(AAS),
∴AE=AF,
在Rt△ADE和Rt△ADF中
,
∴Rt△ADE≌Rt△ADF(HL),
∴∠BDA=∠CDA.
(2)结论还成立,
理由是:过A作AE⊥BD于E,AF⊥DC于F,
∵AE⊥BD,AF⊥DC,
∴∠AED=∠F=90°,
∵∠BDC=120°,
∴∠EAF+∠BDC=180°,
∵∠BAC+∠BDC=180°,
∴∠EAF=∠BAC,
∴∠EAF﹣∠EAC=∠BAC﹣∠EAC,
∴∠BAE=∠CAF,
在△BAE和△CAF中
,
∴△BAE≌△CAF(AAS),
∴AE=AF,
在Rt△ADE和Rt△ADF中
,
∴Rt△ADE≌Rt△ADF(HL),
∴∠BDA=∠CDA,
即结论仍成立.
