2023-2024学年人教版九年级数学上册第21章 一元二次方程 单元复习练习题(含答案)
文档属性
| 名称 | 2023-2024学年人教版九年级数学上册第21章 一元二次方程 单元复习练习题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 41.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-05 21:41:10 | ||
图片预览


文档简介
第21章 一元二次方程
一、单项选择题
1.若关于x的方程a(x-1)2=2x2-2是一元二次方程,则a的值( )
A.等于2 B.等于-2 C.等于0 D.不等于2
2.一元二次方程x2-4x-8=0的解是( )
A.x1=-2+2,x2=-2-2 B.x1=2+2,x2=2-2
C.x1=2+2,x2=2-2 D.x1=2,x2=-2
3.若关于x的方程x2+2x-3=0与=有一个解相同,则a的值为( )
A.1 B.1或-3 C.-1 D.-1或3
4.下列一元二次方程中,有两个不相等实数根的是( )
A.x2-x+=0 B.x2+2x+4=0 C.x2-x+2=0 D.x2-2x=0
5.一元二次方程x2-3x+1=0的根的情况( )
A.有两个相等的实数根 B.有两个不相等的实数根
C.没有实数根 D.无法确定
6.已知关于x的一元二次方程(m-1)x2+2x-3=0有实数根,则m的取值范围( )
A.m≥ B.m< C.m>且m≠1 D.m≥且m≠1
7.若x1+x2=3,x12+x22=5,则以x1,x2为根的一元二次方程是( )
A.x2-3x+2=0 B.x2+3x-2=0 C.x2+3x+2=0 D.x2-3x-2=0
8. 用换元法解方程:--2=0时,如果设=y,那么将原方程变形后表示为一元二次方程一般形式的是( )
A.y--2=0 B.y--1=0 C.y2-2y-1=0 D.y2-y-2=0
9. 若关于x的一元二次方程(k+1)x2+2(k+1)x+k-2=0有实数根,则k的取值范围在数轴上表示正确的是( )
10. 若菱形ABCD的一条对角线长为8,边CD的长是方程x2-10x+24=0的一个根,则该菱形ABCD的周长为( )
A.16 B.24 C.16或24 D.48
二、填空题
11.已知关于x的一元二次方程(a-1)x2-2x+a2-1=0有一个根为x=0,则a=______.
12.一元二次方程(x-2)(x+7)=0的根是____________________.
13.若关于x的一元二次方程x2-2x+k=0有实数根,则实数k的取值范围是__________.
14.若关于x的一元二次方程x2+bx+c=0的两根分别为-2和6,则多项式x2+bx+c因式分解的结果是__________________.
15. 对于实数a,b,定义运算:a*b=关于x的方程(2x+1)*(2x-3)=t恰好有两个不相等的实数根,则t的取值范围是____________.
16.《田亩比类乘除捷法》是我国古代数学家杨辉的著作,其中有一个数学问题:“直田积八百九十一步,只云长阔共六十步,问长多阔几何”.意思是:一块矩形田地的面积为891平方步,只知道它的长与宽共60步,问它的长比宽多多少步?根据题意得,长比宽多__________步.
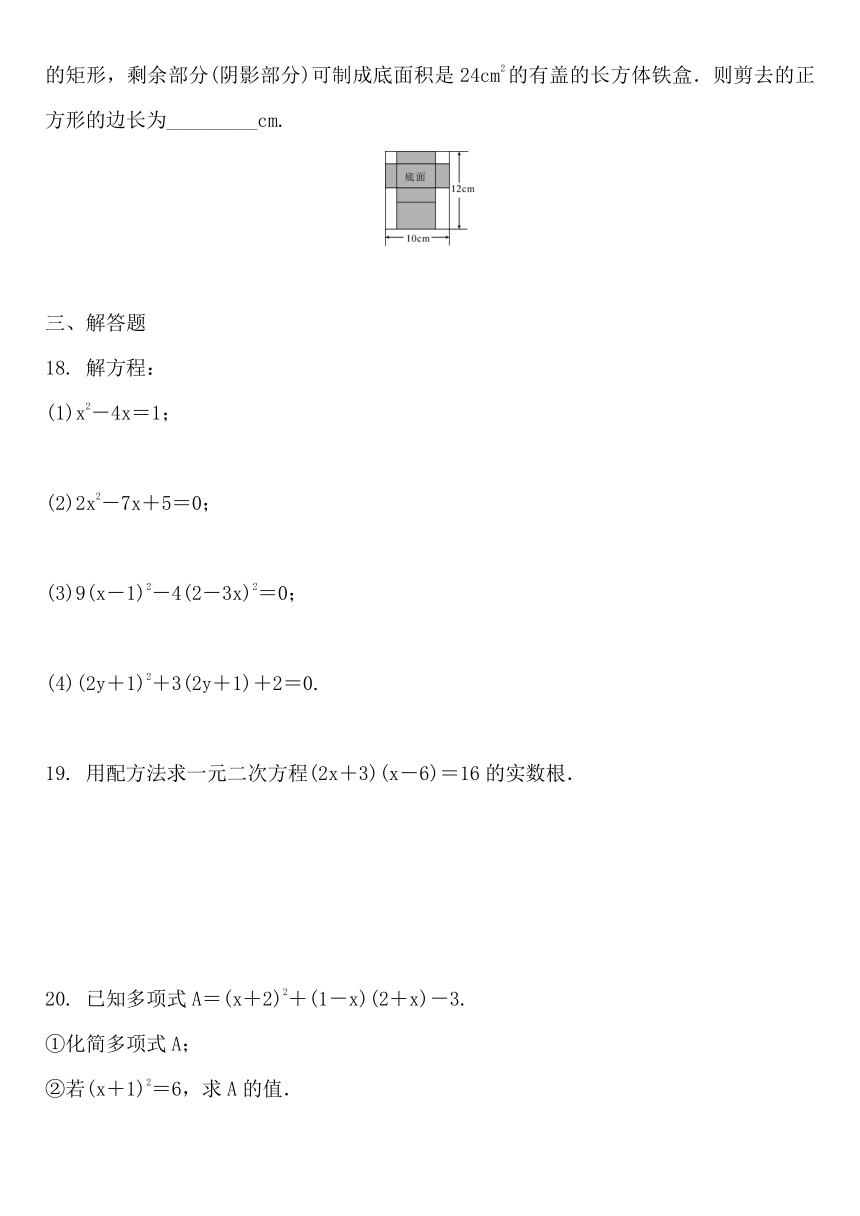
17.如图是一张长12cm,宽10cm的矩形铁皮,将其剪去两个全等的正方形和两个全等的矩形,剩余部分(阴影部分)可制成底面积是24cm2的有盖的长方体铁盒.则剪去的正方形的边长为_________cm.
三、解答题
18. 解方程:
(1)x2-4x=1;
(2)2x2-7x+5=0;
(3)9(x-1)2-4(2-3x)2=0;
(4)(2y+1)2+3(2y+1)+2=0.
19. 用配方法求一元二次方程(2x+3)(x-6)=16的实数根.
20. 已知多项式A=(x+2)2+(1-x)(2+x)-3.
①化简多项式A;
②若(x+1)2=6,求A的值.
21. 重庆小面是重庆美食的名片之一,深受外地游客和本地民众欢迎.某面馆向食客推出经典特色重庆小面,顾客可到店食用(简称“堂食”小面),也可购买搭配佐料的袋装生面(简称“生食”小面).已知3份“堂食”小面和2份“生食”小面的总售价为31元,4份“堂食”小面和1份“生食”小面的总售价为33元.
(1)求每份“堂食”小面和“生食”小面的价格分别是多少元;
(2)该面馆在4月共卖出“堂食”小面4500份,“生食”小面2500份.为回馈广大食客,该面馆从5月1日起每份“堂食”小面的价格保持不变,每份“生食”小面的价格降低a%.统计5月的销量和销售额发现:“堂食”小面的销量与4月相同,“生食”小面的销量在4月的基础上增加a%,这两种小面的总销售额在4月的基础上增加a%.求a的值.
22. 某市创建“绿色发展模范城市”,针对境内长江段两种主要污染源:生活污水和沿江工厂污染物排放,分别用“生活污水集中处理”(下称甲方案)和“沿江工厂转型升级”(下称乙方案)进行治理,若江水污染指数记为Q,沿江工厂用乙方案进行一次性治理(当年完工),从当年开始,所治理的每家工厂一年降低的Q值都以平均值n计算.第一年有40家工厂用乙方案治理,共使Q值降低了12.经过三年治理,境内长江水质明显改善.
(1)求n的值;
(2)从第二年起,每年用乙方案新治理的工厂数量比上一年都增加相同的百分数m,三年来用乙方案治理的工厂数量共190家,求m的值,并计算第二年用乙方案新治理的工厂数量;
(3)该市生活污水用甲方案治理,从第二年起,每年因此降低的Q值比上一年都增加一个相同的数值a.在(2)的情况下,第二年,用乙方案所治理的工厂合计降低的Q值与当年用甲方案治理降低的Q值相等,第三年,用甲方案使Q值降低了39.5.求第一年用甲方案治理降低的Q值及a的值.
答案:
一、
1-10 DBCDB DACAA
二、
11. -1
12. x1=2,x2=-7
13. k≤1
14. (x+2)(x-6)
15. t >-
16. 6
17. 2
三、
18. 解:(1) x1=+2,x2=-+2
(2) x1=,x2=1
(3) x1=,x2=
(4) y1=-,y2=-1
19. 解:原方程化为一般形式为2x2-9x-34=0,x2-x=17,x2-x+=17+,(x-)2=,x-=±,∴x1=,x2=
20. 解:①A=3x+3
②A=±3
21. 解:(1)设每份“堂食”小面的价格为x元,每份“生食”小面的价格为y元,根据题意得:解得答:每份“堂食”小面的价格为7元,每份“生食”小面的价格为5元
(2)由题意得:
4500×7+2500(1+a%)×5(1-a%)=(4500×7+2500×5)(1+a%),
设a%=m,则方程可化为:9×7+25(1+m)(1-m)=(9×7+25)(1+m),
375m2-30m=0,m(25m-2)=0,解得m1=0(舍去),m2=,∴a=8
22. 解:(1) 由题意可得40n=12,解得n=0.3
(2) 由题意可得40+40(1+m)+40(1+m)2=190,解得m1==50%,m2=-(舍去),∴第二年用乙方案新治理的工厂数量为:40(1+m)=40(1+50%)=60(家)
(3)第二年Q值用乙方案治理降低了(40+60)n=100×0.3=30,30+a=39.5,
解得a=9.5,则第一年降低的Q值为30-9.5=20.5
一、单项选择题
1.若关于x的方程a(x-1)2=2x2-2是一元二次方程,则a的值( )
A.等于2 B.等于-2 C.等于0 D.不等于2
2.一元二次方程x2-4x-8=0的解是( )
A.x1=-2+2,x2=-2-2 B.x1=2+2,x2=2-2
C.x1=2+2,x2=2-2 D.x1=2,x2=-2
3.若关于x的方程x2+2x-3=0与=有一个解相同,则a的值为( )
A.1 B.1或-3 C.-1 D.-1或3
4.下列一元二次方程中,有两个不相等实数根的是( )
A.x2-x+=0 B.x2+2x+4=0 C.x2-x+2=0 D.x2-2x=0
5.一元二次方程x2-3x+1=0的根的情况( )
A.有两个相等的实数根 B.有两个不相等的实数根
C.没有实数根 D.无法确定
6.已知关于x的一元二次方程(m-1)x2+2x-3=0有实数根,则m的取值范围( )
A.m≥ B.m< C.m>且m≠1 D.m≥且m≠1
7.若x1+x2=3,x12+x22=5,则以x1,x2为根的一元二次方程是( )
A.x2-3x+2=0 B.x2+3x-2=0 C.x2+3x+2=0 D.x2-3x-2=0
8. 用换元法解方程:--2=0时,如果设=y,那么将原方程变形后表示为一元二次方程一般形式的是( )
A.y--2=0 B.y--1=0 C.y2-2y-1=0 D.y2-y-2=0
9. 若关于x的一元二次方程(k+1)x2+2(k+1)x+k-2=0有实数根,则k的取值范围在数轴上表示正确的是( )
10. 若菱形ABCD的一条对角线长为8,边CD的长是方程x2-10x+24=0的一个根,则该菱形ABCD的周长为( )
A.16 B.24 C.16或24 D.48
二、填空题
11.已知关于x的一元二次方程(a-1)x2-2x+a2-1=0有一个根为x=0,则a=______.
12.一元二次方程(x-2)(x+7)=0的根是____________________.
13.若关于x的一元二次方程x2-2x+k=0有实数根,则实数k的取值范围是__________.
14.若关于x的一元二次方程x2+bx+c=0的两根分别为-2和6,则多项式x2+bx+c因式分解的结果是__________________.
15. 对于实数a,b,定义运算:a*b=关于x的方程(2x+1)*(2x-3)=t恰好有两个不相等的实数根,则t的取值范围是____________.
16.《田亩比类乘除捷法》是我国古代数学家杨辉的著作,其中有一个数学问题:“直田积八百九十一步,只云长阔共六十步,问长多阔几何”.意思是:一块矩形田地的面积为891平方步,只知道它的长与宽共60步,问它的长比宽多多少步?根据题意得,长比宽多__________步.
17.如图是一张长12cm,宽10cm的矩形铁皮,将其剪去两个全等的正方形和两个全等的矩形,剩余部分(阴影部分)可制成底面积是24cm2的有盖的长方体铁盒.则剪去的正方形的边长为_________cm.
三、解答题
18. 解方程:
(1)x2-4x=1;
(2)2x2-7x+5=0;
(3)9(x-1)2-4(2-3x)2=0;
(4)(2y+1)2+3(2y+1)+2=0.
19. 用配方法求一元二次方程(2x+3)(x-6)=16的实数根.
20. 已知多项式A=(x+2)2+(1-x)(2+x)-3.
①化简多项式A;
②若(x+1)2=6,求A的值.
21. 重庆小面是重庆美食的名片之一,深受外地游客和本地民众欢迎.某面馆向食客推出经典特色重庆小面,顾客可到店食用(简称“堂食”小面),也可购买搭配佐料的袋装生面(简称“生食”小面).已知3份“堂食”小面和2份“生食”小面的总售价为31元,4份“堂食”小面和1份“生食”小面的总售价为33元.
(1)求每份“堂食”小面和“生食”小面的价格分别是多少元;
(2)该面馆在4月共卖出“堂食”小面4500份,“生食”小面2500份.为回馈广大食客,该面馆从5月1日起每份“堂食”小面的价格保持不变,每份“生食”小面的价格降低a%.统计5月的销量和销售额发现:“堂食”小面的销量与4月相同,“生食”小面的销量在4月的基础上增加a%,这两种小面的总销售额在4月的基础上增加a%.求a的值.
22. 某市创建“绿色发展模范城市”,针对境内长江段两种主要污染源:生活污水和沿江工厂污染物排放,分别用“生活污水集中处理”(下称甲方案)和“沿江工厂转型升级”(下称乙方案)进行治理,若江水污染指数记为Q,沿江工厂用乙方案进行一次性治理(当年完工),从当年开始,所治理的每家工厂一年降低的Q值都以平均值n计算.第一年有40家工厂用乙方案治理,共使Q值降低了12.经过三年治理,境内长江水质明显改善.
(1)求n的值;
(2)从第二年起,每年用乙方案新治理的工厂数量比上一年都增加相同的百分数m,三年来用乙方案治理的工厂数量共190家,求m的值,并计算第二年用乙方案新治理的工厂数量;
(3)该市生活污水用甲方案治理,从第二年起,每年因此降低的Q值比上一年都增加一个相同的数值a.在(2)的情况下,第二年,用乙方案所治理的工厂合计降低的Q值与当年用甲方案治理降低的Q值相等,第三年,用甲方案使Q值降低了39.5.求第一年用甲方案治理降低的Q值及a的值.
答案:
一、
1-10 DBCDB DACAA
二、
11. -1
12. x1=2,x2=-7
13. k≤1
14. (x+2)(x-6)
15. t >-
16. 6
17. 2
三、
18. 解:(1) x1=+2,x2=-+2
(2) x1=,x2=1
(3) x1=,x2=
(4) y1=-,y2=-1
19. 解:原方程化为一般形式为2x2-9x-34=0,x2-x=17,x2-x+=17+,(x-)2=,x-=±,∴x1=,x2=
20. 解:①A=3x+3
②A=±3
21. 解:(1)设每份“堂食”小面的价格为x元,每份“生食”小面的价格为y元,根据题意得:解得答:每份“堂食”小面的价格为7元,每份“生食”小面的价格为5元
(2)由题意得:
4500×7+2500(1+a%)×5(1-a%)=(4500×7+2500×5)(1+a%),
设a%=m,则方程可化为:9×7+25(1+m)(1-m)=(9×7+25)(1+m),
375m2-30m=0,m(25m-2)=0,解得m1=0(舍去),m2=,∴a=8
22. 解:(1) 由题意可得40n=12,解得n=0.3
(2) 由题意可得40+40(1+m)+40(1+m)2=190,解得m1==50%,m2=-(舍去),∴第二年用乙方案新治理的工厂数量为:40(1+m)=40(1+50%)=60(家)
(3)第二年Q值用乙方案治理降低了(40+60)n=100×0.3=30,30+a=39.5,
解得a=9.5,则第一年降低的Q值为30-9.5=20.5
同课章节目录
