福建省莆田重点中学2024届高三上学期第一次月考数学试题(含解析)
文档属性
| 名称 | 福建省莆田重点中学2024届高三上学期第一次月考数学试题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-05 07:38:59 | ||
图片预览




文档简介
2023-2024学年上学期高三第一次月考试卷
数 学
(考试时间:120分钟 满分:150分)
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 设集合,,则( )
A. B. C. D.
2. 已知函数的定义域是R,则的取值范围是( )
A. B. C. D.
3. 设,则“”是“”的( )
A. 充分非必要条件 B. 必要非充分条件
C. 充要条件 D. 既非充分也非必要条件
4. 设随机变量服从正态分布,若,则a的值为( )
A. 9 B. 7 C. 5 D. 4
5. 若函数在R上是增函数,则实数a取值范围为( )
A. B. C. D.
6. 已知函数,若,则( )
A. B. C. D.
7. 设,则的大小关系为( )
A. B.
C. D.
8. 若函数有两个极值点,且,则( )
A. B. C. D.
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9. 下列结论中,所有正确的结论是( )
A. 若,则
B. 命题的否定是:
C. 若且,则
D. 若,则实数
10. 某国产杀毒软件的比赛规则为每个软件进行四轮考核,每轮考核中能够准确对病毒进行查杀的进入下一轮考核,否则被淘汰.已知某个软件在四轮考核中能够准确杀毒的概率依次是且各轮考核能否通过互不影响,则( )
A. 该软件通过考核的概率为
B. 该软件在第三轮考核被淘汰的概率为
C. 该软件至少能够通过两轮考核的概率为
D. 在此次比赛中该软件平均考核了轮
11. 已知函数在R上可导且,其导函数满足,对于函数,下列结论正确是( )
A. 函数在上为增函数
B. x=-1是函数的极小值点
C. 函数必有2个零点
D.
12. 如图,已知正方体的棱长为,为底面内(包括边界)的动点,则下列结论正确的是( ).
A. 三棱锥的体积为定值
B. 存在点,使得
C. 若,则点在正方形底面内的运动轨迹长为
D. 若点是的中点,点是的中点,过,作平面平面,则平面截正方体的截面面积为
三、填空题:本题共4小题,每小题5分,共20分.
13. “”是真命题,则m的范围是______
14. 已知圆锥的底面半径为1,其侧面展开图为一个半圆,则该圆锥的体积为______.
15 已知随机变量服从正态分布,且,则___________.(附:若,则,,)
16. 已知三棱锥S ABC的所有顶点都在球O的球面上,SC是球O的直径.若平面SCA⊥平面SCB,SA=AC,SB=BC,三棱锥S ABC的体积为9,则球O的体积为____________.
四、解答题:本题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.
17. 计算下列各式的值:
(1);
(2).
18. 已知函数在处的切线方程为.
(1)求的解析式;
(2)求函数图象上的点到直线的距离的最小值.
19. 鲜花饼是以云南特有的食用玫瑰花入料的酥饼,是具有云南特色的云南经典点心代表,鲜花饼的保质期一般在三至四天.据统计,某超市一天鲜花饼卖出3箱的概率为,卖出箱的概率为,卖出箱的概率为,没有卖出的概率为,为了保证顾客能够买到新鲜的鲜花饼,该超市规定当天结束营业后检查货架上存货,若卖出箱及以上,则需补货至箱,否则不补货.假设第一天该超市开始营业时货架上有箱鲜花饼.
(1)在第一天结束营业后货架上有箱鲜花饼的条件下,求第二天结束营业时货架上有箱存货的概率;
(2)求第二天结束营业时货架上有箱存货的概率.
20. 如图所示,正方形和矩形所在的平面互相垂直,动点在线段(包含端点,)上,,分别为,的中点,.
(1)若为的中点,求点到平面的距离;
(2)设平面与平面所成的锐角为,求的最大值并求出此时点的位置.
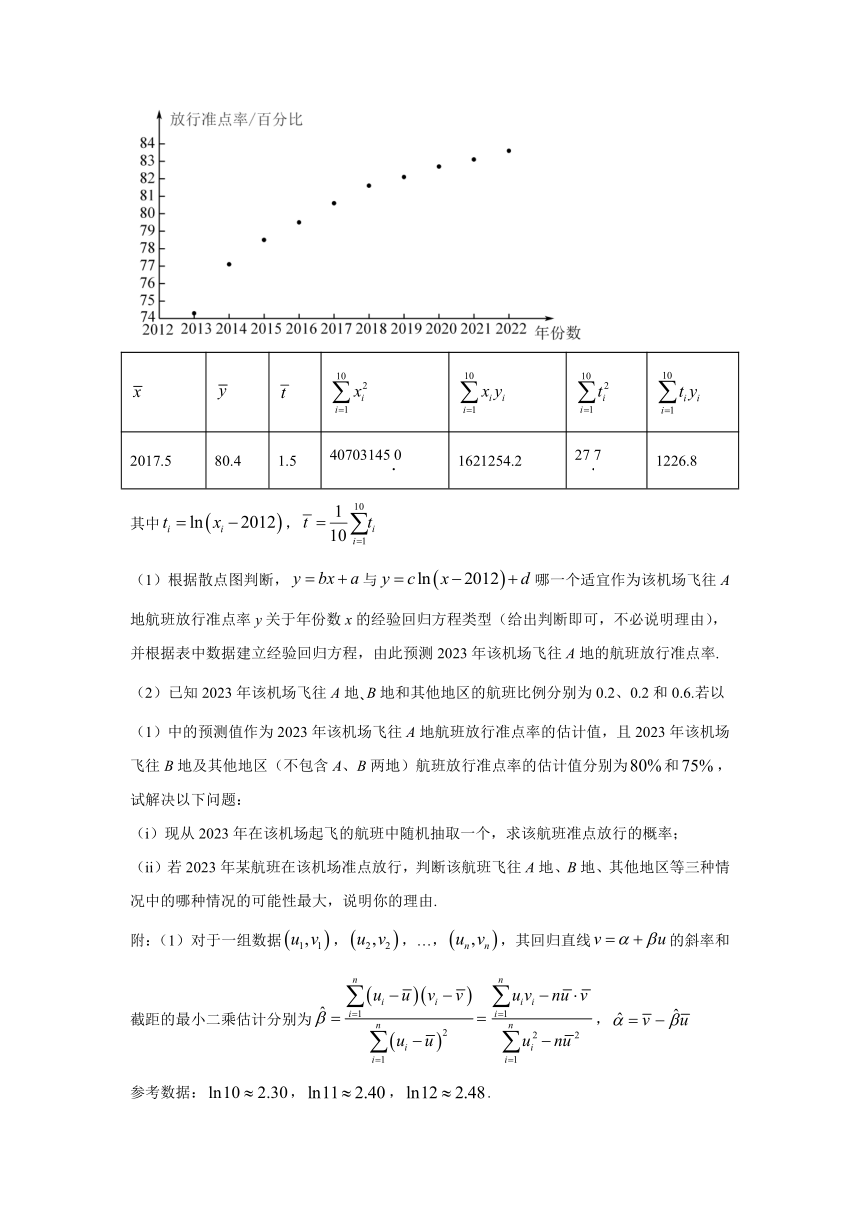
21. 放行准点率是衡量机场运行效率和服务质量的重要指标之一.某机场自2012年起采取相关策略优化各个服务环节,运行效率不断提升.以下是根据近10年年份数与该机场飞往A地航班放行准点率()(单位:百分比)的统计数据所作的散点图及经过初步处理后得到的一些统计量的值.
2017.5 80.4 1.5 407031450 1621254.2 277 1226.8
其中,
(1)根据散点图判断,与哪一个适宜作为该机场飞往A地航班放行准点率y关于年份数x的经验回归方程类型(给出判断即可,不必说明理由),并根据表中数据建立经验回归方程,由此预测2023年该机场飞往A地的航班放行准点率.
(2)已知2023年该机场飞往A地 B地和其他地区的航班比例分别为0.2、0.2和0.6.若以(1)中的预测值作为2023年该机场飞往A地航班放行准点率的估计值,且2023年该机场飞往B地及其他地区(不包含A、B两地)航班放行准点率的估计值分别为和,试解决以下问题:
(i)现从2023年在该机场起飞的航班中随机抽取一个,求该航班准点放行的概率;
(ii)若2023年某航班在该机场准点放行,判断该航班飞往A地、B地、其他地区等三种情况中的哪种情况的可能性最大,说明你的理由.
附:(1)对于一组数据,,…,,其回归直线的斜率和截距的最小二乘估计分别为,
参考数据:,,.
22. 已知函数有最大值,,且是 的导数.
(Ⅰ)求的值;
(Ⅱ)证明:当,时,
1. 设集合,,则( )
A. B. C. D.
【答案】C
【解析】
【分析】分别求出集合,再根据交集的定义求解即可.
【详解】解:因为,,
所以.
故选:C.
2. 已知函数的定义域是R,则的取值范围是( )
A. B. C. D.
【答案】C
【解析】
【分析】根据给定条件,建立恒成立的不等式,再分类讨论求解作答.
【详解】依题意,,不等式恒成立,
当时,恒成立,则,
当时,有,解得,则,因此
所以的取值范围是.
故选:C
3. 设,则“”是“”的( )
A. 充分非必要条件 B. 必要非充分条件
C. 充要条件 D. 既非充分也非必要条件
【答案】A
【解析】
【分析】根据给定条件,利用充分条件、必要条件的定义判断作答.
【详解】由得或,因此“若,则”是真命题,“若,则”是假命题,
所以“”是“”的充分不必要条件.
故选:A
4. 设随机变量服从正态分布,若,则a的值为( )
A. 9 B. 7 C. 5 D. 4
【答案】B
【解析】
【分析】根据正态分布概率密度函数的对称性即可求解.
【详解】由题意,根据正态分布对称性,
得,
解得,
故选:B.
5. 若函数在R上是增函数,则实数a的取值范围为( )
A. B. C. D.
【答案】B
【解析】
【分析】原命题等价为在R上恒成立,结合二次函数的性质列不等式求解即可.
【详解】∵函数在R上是增函数,在R上恒成立,
∴.
故选:B.
6. 已知函数,若,则( )
A. B. C. D.
【答案】C
【解析】
【分析】得出即可
【详解】因为
所以
即,因为,所以
故选:C
7. 设,则的大小关系为( )
A. B.
C. D.
【答案】B
【解析】
【分析】根据指数函数与对数函数的单调性比较大小即可.
【详解】是单调递增函数,,,
,
是单调递减函数
,
,
故选:B
8. 若函数有两个极值点,且,则( )
A. B. C. D.
【答案】C
【解析】
【分析】由极值点定义确定的关系,化简,由此求的范围.
【详解】因为函数有两个极值点,
又函数的定义域为,导函数为,
所以方程由两个不同的正根,且为其根,
所以,,,
所以,
则
,
又,即,可得,
所以或(舍去),
故选:C.
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9. 下列结论中,所有正确的结论是( )
A. 若,则
B. 命题的否定是:
C. 若且,则
D. 若,则实数
【答案】AB
【解析】
【分析】对A,根据不等式的性质推导即可;对B,根据特称命题的否定为全称命题判断即可;对C,利用作差法判断即可;对D,举反例判断即可.
【详解】对A,,则,又,则,,故A正确;
对B,命题的否定是:,故B正确;
对C,,因为且,故,即,故C错误;
对D,当,时,不成立,故D错误;
故选:AB
10. 某国产杀毒软件的比赛规则为每个软件进行四轮考核,每轮考核中能够准确对病毒进行查杀的进入下一轮考核,否则被淘汰.已知某个软件在四轮考核中能够准确杀毒的概率依次是且各轮考核能否通过互不影响,则( )
A. 该软件通过考核概率为
B. 该软件在第三轮考核被淘汰的概率为
C. 该软件至少能够通过两轮考核的概率为
D. 在此次比赛中该软件平均考核了轮
【答案】ABD
【解析】
【分析】设事件,2,3,表示“该软件能通过第轮考核”,由已知可得,,,,再利用互斥事件概率加法公式、相互独立事件概率乘法公式以及对立事件的概率公式一一计算可得.
【详解】解:设事件,2,3,表示“该软件能通过第轮考核”,
由已知得,,,,
该软件通过考核的概率为;
该软件在第三轮考核被淘汰的概率为,故选项B正确;
该软件至少能够通过两轮考核的概率为,故选项C不正确;设在此次比赛中,该软件考核了轮,∴的可能取值为1,2,3,4,,,,,∴,故选项D正确.
故选:ABD
11. 已知函数在R上可导且,其导函数满足,对于函数,下列结论正确的是( )
A. 函数在上为增函数
B. x=-1是函数的极小值点
C. 函数必有2个零点
D.
【答案】ABD
【解析】
【分析】,所以使用分类讨论的方法就可以判断出的单调性,极值,零点问题.
【详解】∵,,
∴时,,;
在上时是增函数,故A正确;
时,,,
在上时是减函数,在x=-1时,取得极小值,故B正确;
若,则没有零点;
若,则只有一个零点;
若,则才有两个零点,故C错误;
∵在上是增函数,∴,
即,∴,故D正确;
故答案为:ABD.
12. 如图,已知正方体的棱长为,为底面内(包括边界)的动点,则下列结论正确的是( ).
A. 三棱锥的体积为定值
B. 存在点,使得
C. 若,则点在正方形底面内的运动轨迹长为
D. 若点是的中点,点是的中点,过,作平面平面,则平面截正方体的截面面积为
【答案】ABD
【解析】
【分析】根据等体积法可计算出三棱锥的体积,可判断选项A,建立空间直角坐标系,写出对应点的坐标与向量的坐标,设,根据垂直得向量数量积为列式,从而判断选项B,C,利用线面垂直的判定定理得平面,再证明四点共面,从而得平面,再由面面平行的性质可得平面截正方体的截面为正六边形,根据正六边形的性质计算面积即可判断选项D.
【详解】对于A,由等体积法,三棱锥的高为,
底面积,所以,
所以三棱锥的体积为定值,A正确;
对于B,建立如图所示的空间直角坐标系,
设,,,,,,
,,
若,则,
即,取,此时点与点重合,满足题意,
所以存在点,使得,B正确;
对于C,,若,
,即,
所以点的轨迹就是线段,
轨迹长为,C错误;
对于D,如图取中点,连接,
由题可得,平面,
连接,因为,平面,
则,,又,
平面,则平面,
又取中点为,则,
有四点共面,则平面即为平面,
又由两平面平行性质可知,,,,
又都是中点,故是中点,是中点,
则平面截正方体的截面为正六边形,
又正方体棱长为,则,
故截面面积为,D正确.
故选:ABD
三、填空题:本题共4小题,每小题5分,共20分.
13. “”是真命题,则m的范围是______
【答案】
【解析】
【分析】由题知,由x的取值范围得到1-x的取值范围,进而根据全称命题的意义即可得答案;
【详解】对于命题:对任意,不等式恒成立,
而,有,
∴,∴命题为真时,实数m的取值范围是.
故答案为:
14. 已知圆锥的底面半径为1,其侧面展开图为一个半圆,则该圆锥的体积为______.
【答案】##
【解析】
【分析】先计算圆锥的底面周长,即为侧面展开图的弧长,进而求得侧面展开图的半径,即为圆锥的母线长,再求得圆锥的高,从而求得体积即可
【详解】∵圆锥的底面半径为1,∴侧面展开图的弧长为,
又∵侧面展开图是半圆,∴侧面展开图的半径为2,即圆锥的母线长为2,故圆锥的高为,故体积
故答案为:
15. 已知随机变量服从正态分布,且,则___________.(附:若,则,,)
【答案】0.00135
【解析】
【分析】利用已知条件,求解,然后利用正态分布的性质求解即可.
【详解】又,则,
随机变量服从正态分布,且,
即,所以,即,,即,
所以,所以.
故答案为:0.00135.
16. 已知三棱锥S ABC的所有顶点都在球O的球面上,SC是球O的直径.若平面SCA⊥平面SCB,SA=AC,SB=BC,三棱锥S ABC的体积为9,则球O的体积为____________.
【答案】36π
【解析】
【分析】
先由已知条件证明OA⊥平面SCB,确定三棱锥S ABC的高,利用体积构建关系解得半径,再求球的体积即可.
【详解】如图,
连接OA,OB.
由SA=AC,SB=BC,SC为球O的直径,知OA⊥SC,OB⊥SC.
又由平面SCA⊥平面SCB,平面SCA∩平面SCB=SC,知OA⊥平面SCB.
设球O的半径为r,则OA=OB=r,SC=2r,
所以三棱锥S ABC的体积为,
即=9.所以r=3. 所以球的体积
故答案为:36π.
四、解答题:本题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.
17. 计算下列各式的值:
(1);
(2).
【答案】(1)
(2)
【解析】
【分析】根据指数和对数运算法则直接化简求解即可.
【小问1详解】
.
【小问2详解】
.
18. 已知函数在处的切线方程为.
(1)求的解析式;
(2)求函数图象上的点到直线的距离的最小值.
【答案】(1);
(2).
【解析】
【分析】(1)由题可得,然后利用导数的几何意义即求;
(2)由题可得切点到直线的距离最小,即得.
【小问1详解】
∵函数,
∴的定义域为,,
∴在处切线的斜率为,
由切线方程可知切点为,而切点也在函数图象上,解得,
∴的解析式为;
【小问2详解】
由于直线与直线平行,直线与函数在处相切,
所以切点到直线的距离最小,最小值为,
故函数图象上的点到直线的距离的最小值为.
19. 鲜花饼是以云南特有的食用玫瑰花入料的酥饼,是具有云南特色的云南经典点心代表,鲜花饼的保质期一般在三至四天.据统计,某超市一天鲜花饼卖出3箱的概率为,卖出箱的概率为,卖出箱的概率为,没有卖出的概率为,为了保证顾客能够买到新鲜的鲜花饼,该超市规定当天结束营业后检查货架上存货,若卖出箱及以上,则需补货至箱,否则不补货.假设第一天该超市开始营业时货架上有箱鲜花饼.
(1)在第一天结束营业后货架上有箱鲜花饼的条件下,求第二天结束营业时货架上有箱存货的概率;
(2)求第二天结束营业时货架上有箱存货的概率.
【答案】(1)
(2)
【解析】
【分析】(1)利用条件概率的概念直接计算;
(2)利用全公式直接计算.
【小问1详解】
设事件:“第二天开始营业时货架上有箱鲜花饼”,事件:“第二天开始营业时货架上有箱鲜花饼”,,事件:“第二天结束营业时货架上有箱存货”,
因为第一天结束营业后货架上有箱鲜花饼,故第二天只卖出箱,
故;
【小问2详解】
由题意,,,
由全概率公式得.
20. 如图所示,正方形和矩形所在的平面互相垂直,动点在线段(包含端点,)上,,分别为,的中点,.
(1)若为的中点,求点到平面的距离;
(2)设平面与平面所成的锐角为,求的最大值并求出此时点的位置.
【答案】(1)
(2)最大值为,此时点与点重合
【解析】
【分析】(1)以点A为坐标原点,以AB、AD、AF所在直线为x、y、z轴,建立空间直角坐标系,利用向量法求出点N到平面PDM的距离;
(2)设,则,,求出平面PDM的法向量和平面ABCD的法向量,利用向量法求出的最大值,此时P点与F点重合.
【小问1详解】
解析:以A点为坐标原点,以,,的方向分别为x轴、y轴、z轴的正方向,建立空间直角坐标系.
由图可得,,,,
则,,.
设平面PDM的一个法向量为,
由,
可得.
设点N到平面PDM的距离为d,
则.
【小问2详解】
解:因为动点P在线段EF(包含端点E,F)上,
可设,
则,.
设平面PDM的一个法向量为,
由,
可得.
因为平面ABCD的一个法向量,
,
所以当时,取得最大值,此时P点与F点重合.
21. 放行准点率是衡量机场运行效率和服务质量的重要指标之一.某机场自2012年起采取相关策略优化各个服务环节,运行效率不断提升.以下是根据近10年年份数与该机场飞往A地航班放行准点率()(单位:百分比)的统计数据所作的散点图及经过初步处理后得到的一些统计量的值.
2017.5 80.4 1.5 40703145.0 1621254.2 277 12268
其中,
(1)根据散点图判断,与哪一个适宜作为该机场飞往A地航班放行准点率y关于年份数x的经验回归方程类型(给出判断即可,不必说明理由),并根据表中数据建立经验回归方程,由此预测2023年该机场飞往A地的航班放行准点率.
(2)已知2023年该机场飞往A地 B地和其他地区的航班比例分别为0.2、0.2和0.6.若以(1)中的预测值作为2023年该机场飞往A地航班放行准点率的估计值,且2023年该机场飞往B地及其他地区(不包含A、B两地)航班放行准点率的估计值分别为和,试解决以下问题:
(i)现从2023年在该机场起飞的航班中随机抽取一个,求该航班准点放行的概率;
(ii)若2023年某航班在该机场准点放行,判断该航班飞往A地、B地、其他地区等三种情况中的哪种情况的可能性最大,说明你的理由.
附:(1)对于一组数据,,…,,其回归直线的斜率和截距的最小二乘估计分别为,
参考数据:,,.
【答案】(1)适宜,预测2023年该机场飞往A地的航班放行准点率
(2)(i)0.778;(ii)可判断该航班飞往其他地区的可能性最大,理由见解析
【解析】
【分析】(1)根据线性回归方程的计算公式,选择合适的模型计算即可;
(2)利用全概率公式和条件概率公式,即可根据概率判断可能性最大的情况.
【小问1详解】
由散点图判断适宜作为该机场飞往A地航班放行准点率y关于年份数x的经验回归方程类型.
令,先建立y关于t的线性回归方程.
由于,
,
该机场飞往A地航班放行准点率y关于t的线性回归方程为,
因此y关于年份数x的回归方程为
所以当时,该机场飞往A地航班放行准点率y的预报值为
.
所以2023年该机场飞往A地航班放行准点率y的预报值为.
【小问2详解】
设“该航班飞往A地”,“该航班飞往B地”,“该航班飞往其他地区”,“该航班准点放行”,
则,,,
,,.
(i)由全概率公式得,
,
所以该航班准点放行的概率为0.778.
(ii),
,
,
因为,
所以可判断该航班飞往其他地区的可能性最大.
22. 已知函数有最大值,,且是 的导数.
(Ⅰ)求的值;
(Ⅱ)证明:当,时,.
【答案】(Ⅰ);(Ⅱ)见解析.
【解析】
【详解】试题分析:(Ⅰ)函数求导,讨论函数单调性求最值即可;
(Ⅱ)由(Ⅰ)可知,,求导得在上单调递增,由且得,由,单调递增,要证,即,只要证,即,所以只要证,构造函数求导证明即可.
试题解析:
(Ⅰ)的定义域为,.
当时,,
在上为单调递增函数,无最大值,不合题意,舍去;
当时,令,得,
当时,,函数单调递增;
当时,,函数单调递减,
,
,
.
(Ⅱ)由(Ⅰ)可知,,
.
,,
在上单调递增.
又,且,
.
,
当时,,单调递增,
要证,即,只要证,即.
,,
所以只要证 ————(*)
设 (其中),
,
在(0,1)上为增函数,
,故(*)式成立,从而.
数 学
(考试时间:120分钟 满分:150分)
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 设集合,,则( )
A. B. C. D.
2. 已知函数的定义域是R,则的取值范围是( )
A. B. C. D.
3. 设,则“”是“”的( )
A. 充分非必要条件 B. 必要非充分条件
C. 充要条件 D. 既非充分也非必要条件
4. 设随机变量服从正态分布,若,则a的值为( )
A. 9 B. 7 C. 5 D. 4
5. 若函数在R上是增函数,则实数a取值范围为( )
A. B. C. D.
6. 已知函数,若,则( )
A. B. C. D.
7. 设,则的大小关系为( )
A. B.
C. D.
8. 若函数有两个极值点,且,则( )
A. B. C. D.
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9. 下列结论中,所有正确的结论是( )
A. 若,则
B. 命题的否定是:
C. 若且,则
D. 若,则实数
10. 某国产杀毒软件的比赛规则为每个软件进行四轮考核,每轮考核中能够准确对病毒进行查杀的进入下一轮考核,否则被淘汰.已知某个软件在四轮考核中能够准确杀毒的概率依次是且各轮考核能否通过互不影响,则( )
A. 该软件通过考核的概率为
B. 该软件在第三轮考核被淘汰的概率为
C. 该软件至少能够通过两轮考核的概率为
D. 在此次比赛中该软件平均考核了轮
11. 已知函数在R上可导且,其导函数满足,对于函数,下列结论正确是( )
A. 函数在上为增函数
B. x=-1是函数的极小值点
C. 函数必有2个零点
D.
12. 如图,已知正方体的棱长为,为底面内(包括边界)的动点,则下列结论正确的是( ).
A. 三棱锥的体积为定值
B. 存在点,使得
C. 若,则点在正方形底面内的运动轨迹长为
D. 若点是的中点,点是的中点,过,作平面平面,则平面截正方体的截面面积为
三、填空题:本题共4小题,每小题5分,共20分.
13. “”是真命题,则m的范围是______
14. 已知圆锥的底面半径为1,其侧面展开图为一个半圆,则该圆锥的体积为______.
15 已知随机变量服从正态分布,且,则___________.(附:若,则,,)
16. 已知三棱锥S ABC的所有顶点都在球O的球面上,SC是球O的直径.若平面SCA⊥平面SCB,SA=AC,SB=BC,三棱锥S ABC的体积为9,则球O的体积为____________.
四、解答题:本题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.
17. 计算下列各式的值:
(1);
(2).
18. 已知函数在处的切线方程为.
(1)求的解析式;
(2)求函数图象上的点到直线的距离的最小值.
19. 鲜花饼是以云南特有的食用玫瑰花入料的酥饼,是具有云南特色的云南经典点心代表,鲜花饼的保质期一般在三至四天.据统计,某超市一天鲜花饼卖出3箱的概率为,卖出箱的概率为,卖出箱的概率为,没有卖出的概率为,为了保证顾客能够买到新鲜的鲜花饼,该超市规定当天结束营业后检查货架上存货,若卖出箱及以上,则需补货至箱,否则不补货.假设第一天该超市开始营业时货架上有箱鲜花饼.
(1)在第一天结束营业后货架上有箱鲜花饼的条件下,求第二天结束营业时货架上有箱存货的概率;
(2)求第二天结束营业时货架上有箱存货的概率.
20. 如图所示,正方形和矩形所在的平面互相垂直,动点在线段(包含端点,)上,,分别为,的中点,.
(1)若为的中点,求点到平面的距离;
(2)设平面与平面所成的锐角为,求的最大值并求出此时点的位置.
21. 放行准点率是衡量机场运行效率和服务质量的重要指标之一.某机场自2012年起采取相关策略优化各个服务环节,运行效率不断提升.以下是根据近10年年份数与该机场飞往A地航班放行准点率()(单位:百分比)的统计数据所作的散点图及经过初步处理后得到的一些统计量的值.
2017.5 80.4 1.5 407031450 1621254.2 277 1226.8
其中,
(1)根据散点图判断,与哪一个适宜作为该机场飞往A地航班放行准点率y关于年份数x的经验回归方程类型(给出判断即可,不必说明理由),并根据表中数据建立经验回归方程,由此预测2023年该机场飞往A地的航班放行准点率.
(2)已知2023年该机场飞往A地 B地和其他地区的航班比例分别为0.2、0.2和0.6.若以(1)中的预测值作为2023年该机场飞往A地航班放行准点率的估计值,且2023年该机场飞往B地及其他地区(不包含A、B两地)航班放行准点率的估计值分别为和,试解决以下问题:
(i)现从2023年在该机场起飞的航班中随机抽取一个,求该航班准点放行的概率;
(ii)若2023年某航班在该机场准点放行,判断该航班飞往A地、B地、其他地区等三种情况中的哪种情况的可能性最大,说明你的理由.
附:(1)对于一组数据,,…,,其回归直线的斜率和截距的最小二乘估计分别为,
参考数据:,,.
22. 已知函数有最大值,,且是 的导数.
(Ⅰ)求的值;
(Ⅱ)证明:当,时,
1. 设集合,,则( )
A. B. C. D.
【答案】C
【解析】
【分析】分别求出集合,再根据交集的定义求解即可.
【详解】解:因为,,
所以.
故选:C.
2. 已知函数的定义域是R,则的取值范围是( )
A. B. C. D.
【答案】C
【解析】
【分析】根据给定条件,建立恒成立的不等式,再分类讨论求解作答.
【详解】依题意,,不等式恒成立,
当时,恒成立,则,
当时,有,解得,则,因此
所以的取值范围是.
故选:C
3. 设,则“”是“”的( )
A. 充分非必要条件 B. 必要非充分条件
C. 充要条件 D. 既非充分也非必要条件
【答案】A
【解析】
【分析】根据给定条件,利用充分条件、必要条件的定义判断作答.
【详解】由得或,因此“若,则”是真命题,“若,则”是假命题,
所以“”是“”的充分不必要条件.
故选:A
4. 设随机变量服从正态分布,若,则a的值为( )
A. 9 B. 7 C. 5 D. 4
【答案】B
【解析】
【分析】根据正态分布概率密度函数的对称性即可求解.
【详解】由题意,根据正态分布对称性,
得,
解得,
故选:B.
5. 若函数在R上是增函数,则实数a的取值范围为( )
A. B. C. D.
【答案】B
【解析】
【分析】原命题等价为在R上恒成立,结合二次函数的性质列不等式求解即可.
【详解】∵函数在R上是增函数,在R上恒成立,
∴.
故选:B.
6. 已知函数,若,则( )
A. B. C. D.
【答案】C
【解析】
【分析】得出即可
【详解】因为
所以
即,因为,所以
故选:C
7. 设,则的大小关系为( )
A. B.
C. D.
【答案】B
【解析】
【分析】根据指数函数与对数函数的单调性比较大小即可.
【详解】是单调递增函数,,,
,
是单调递减函数
,
,
故选:B
8. 若函数有两个极值点,且,则( )
A. B. C. D.
【答案】C
【解析】
【分析】由极值点定义确定的关系,化简,由此求的范围.
【详解】因为函数有两个极值点,
又函数的定义域为,导函数为,
所以方程由两个不同的正根,且为其根,
所以,,,
所以,
则
,
又,即,可得,
所以或(舍去),
故选:C.
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9. 下列结论中,所有正确的结论是( )
A. 若,则
B. 命题的否定是:
C. 若且,则
D. 若,则实数
【答案】AB
【解析】
【分析】对A,根据不等式的性质推导即可;对B,根据特称命题的否定为全称命题判断即可;对C,利用作差法判断即可;对D,举反例判断即可.
【详解】对A,,则,又,则,,故A正确;
对B,命题的否定是:,故B正确;
对C,,因为且,故,即,故C错误;
对D,当,时,不成立,故D错误;
故选:AB
10. 某国产杀毒软件的比赛规则为每个软件进行四轮考核,每轮考核中能够准确对病毒进行查杀的进入下一轮考核,否则被淘汰.已知某个软件在四轮考核中能够准确杀毒的概率依次是且各轮考核能否通过互不影响,则( )
A. 该软件通过考核概率为
B. 该软件在第三轮考核被淘汰的概率为
C. 该软件至少能够通过两轮考核的概率为
D. 在此次比赛中该软件平均考核了轮
【答案】ABD
【解析】
【分析】设事件,2,3,表示“该软件能通过第轮考核”,由已知可得,,,,再利用互斥事件概率加法公式、相互独立事件概率乘法公式以及对立事件的概率公式一一计算可得.
【详解】解:设事件,2,3,表示“该软件能通过第轮考核”,
由已知得,,,,
该软件通过考核的概率为;
该软件在第三轮考核被淘汰的概率为,故选项B正确;
该软件至少能够通过两轮考核的概率为,故选项C不正确;设在此次比赛中,该软件考核了轮,∴的可能取值为1,2,3,4,,,,,∴,故选项D正确.
故选:ABD
11. 已知函数在R上可导且,其导函数满足,对于函数,下列结论正确的是( )
A. 函数在上为增函数
B. x=-1是函数的极小值点
C. 函数必有2个零点
D.
【答案】ABD
【解析】
【分析】,所以使用分类讨论的方法就可以判断出的单调性,极值,零点问题.
【详解】∵,,
∴时,,;
在上时是增函数,故A正确;
时,,,
在上时是减函数,在x=-1时,取得极小值,故B正确;
若,则没有零点;
若,则只有一个零点;
若,则才有两个零点,故C错误;
∵在上是增函数,∴,
即,∴,故D正确;
故答案为:ABD.
12. 如图,已知正方体的棱长为,为底面内(包括边界)的动点,则下列结论正确的是( ).
A. 三棱锥的体积为定值
B. 存在点,使得
C. 若,则点在正方形底面内的运动轨迹长为
D. 若点是的中点,点是的中点,过,作平面平面,则平面截正方体的截面面积为
【答案】ABD
【解析】
【分析】根据等体积法可计算出三棱锥的体积,可判断选项A,建立空间直角坐标系,写出对应点的坐标与向量的坐标,设,根据垂直得向量数量积为列式,从而判断选项B,C,利用线面垂直的判定定理得平面,再证明四点共面,从而得平面,再由面面平行的性质可得平面截正方体的截面为正六边形,根据正六边形的性质计算面积即可判断选项D.
【详解】对于A,由等体积法,三棱锥的高为,
底面积,所以,
所以三棱锥的体积为定值,A正确;
对于B,建立如图所示的空间直角坐标系,
设,,,,,,
,,
若,则,
即,取,此时点与点重合,满足题意,
所以存在点,使得,B正确;
对于C,,若,
,即,
所以点的轨迹就是线段,
轨迹长为,C错误;
对于D,如图取中点,连接,
由题可得,平面,
连接,因为,平面,
则,,又,
平面,则平面,
又取中点为,则,
有四点共面,则平面即为平面,
又由两平面平行性质可知,,,,
又都是中点,故是中点,是中点,
则平面截正方体的截面为正六边形,
又正方体棱长为,则,
故截面面积为,D正确.
故选:ABD
三、填空题:本题共4小题,每小题5分,共20分.
13. “”是真命题,则m的范围是______
【答案】
【解析】
【分析】由题知,由x的取值范围得到1-x的取值范围,进而根据全称命题的意义即可得答案;
【详解】对于命题:对任意,不等式恒成立,
而,有,
∴,∴命题为真时,实数m的取值范围是.
故答案为:
14. 已知圆锥的底面半径为1,其侧面展开图为一个半圆,则该圆锥的体积为______.
【答案】##
【解析】
【分析】先计算圆锥的底面周长,即为侧面展开图的弧长,进而求得侧面展开图的半径,即为圆锥的母线长,再求得圆锥的高,从而求得体积即可
【详解】∵圆锥的底面半径为1,∴侧面展开图的弧长为,
又∵侧面展开图是半圆,∴侧面展开图的半径为2,即圆锥的母线长为2,故圆锥的高为,故体积
故答案为:
15. 已知随机变量服从正态分布,且,则___________.(附:若,则,,)
【答案】0.00135
【解析】
【分析】利用已知条件,求解,然后利用正态分布的性质求解即可.
【详解】又,则,
随机变量服从正态分布,且,
即,所以,即,,即,
所以,所以.
故答案为:0.00135.
16. 已知三棱锥S ABC的所有顶点都在球O的球面上,SC是球O的直径.若平面SCA⊥平面SCB,SA=AC,SB=BC,三棱锥S ABC的体积为9,则球O的体积为____________.
【答案】36π
【解析】
【分析】
先由已知条件证明OA⊥平面SCB,确定三棱锥S ABC的高,利用体积构建关系解得半径,再求球的体积即可.
【详解】如图,
连接OA,OB.
由SA=AC,SB=BC,SC为球O的直径,知OA⊥SC,OB⊥SC.
又由平面SCA⊥平面SCB,平面SCA∩平面SCB=SC,知OA⊥平面SCB.
设球O的半径为r,则OA=OB=r,SC=2r,
所以三棱锥S ABC的体积为,
即=9.所以r=3. 所以球的体积
故答案为:36π.
四、解答题:本题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.
17. 计算下列各式的值:
(1);
(2).
【答案】(1)
(2)
【解析】
【分析】根据指数和对数运算法则直接化简求解即可.
【小问1详解】
.
【小问2详解】
.
18. 已知函数在处的切线方程为.
(1)求的解析式;
(2)求函数图象上的点到直线的距离的最小值.
【答案】(1);
(2).
【解析】
【分析】(1)由题可得,然后利用导数的几何意义即求;
(2)由题可得切点到直线的距离最小,即得.
【小问1详解】
∵函数,
∴的定义域为,,
∴在处切线的斜率为,
由切线方程可知切点为,而切点也在函数图象上,解得,
∴的解析式为;
【小问2详解】
由于直线与直线平行,直线与函数在处相切,
所以切点到直线的距离最小,最小值为,
故函数图象上的点到直线的距离的最小值为.
19. 鲜花饼是以云南特有的食用玫瑰花入料的酥饼,是具有云南特色的云南经典点心代表,鲜花饼的保质期一般在三至四天.据统计,某超市一天鲜花饼卖出3箱的概率为,卖出箱的概率为,卖出箱的概率为,没有卖出的概率为,为了保证顾客能够买到新鲜的鲜花饼,该超市规定当天结束营业后检查货架上存货,若卖出箱及以上,则需补货至箱,否则不补货.假设第一天该超市开始营业时货架上有箱鲜花饼.
(1)在第一天结束营业后货架上有箱鲜花饼的条件下,求第二天结束营业时货架上有箱存货的概率;
(2)求第二天结束营业时货架上有箱存货的概率.
【答案】(1)
(2)
【解析】
【分析】(1)利用条件概率的概念直接计算;
(2)利用全公式直接计算.
【小问1详解】
设事件:“第二天开始营业时货架上有箱鲜花饼”,事件:“第二天开始营业时货架上有箱鲜花饼”,,事件:“第二天结束营业时货架上有箱存货”,
因为第一天结束营业后货架上有箱鲜花饼,故第二天只卖出箱,
故;
【小问2详解】
由题意,,,
由全概率公式得.
20. 如图所示,正方形和矩形所在的平面互相垂直,动点在线段(包含端点,)上,,分别为,的中点,.
(1)若为的中点,求点到平面的距离;
(2)设平面与平面所成的锐角为,求的最大值并求出此时点的位置.
【答案】(1)
(2)最大值为,此时点与点重合
【解析】
【分析】(1)以点A为坐标原点,以AB、AD、AF所在直线为x、y、z轴,建立空间直角坐标系,利用向量法求出点N到平面PDM的距离;
(2)设,则,,求出平面PDM的法向量和平面ABCD的法向量,利用向量法求出的最大值,此时P点与F点重合.
【小问1详解】
解析:以A点为坐标原点,以,,的方向分别为x轴、y轴、z轴的正方向,建立空间直角坐标系.
由图可得,,,,
则,,.
设平面PDM的一个法向量为,
由,
可得.
设点N到平面PDM的距离为d,
则.
【小问2详解】
解:因为动点P在线段EF(包含端点E,F)上,
可设,
则,.
设平面PDM的一个法向量为,
由,
可得.
因为平面ABCD的一个法向量,
,
所以当时,取得最大值,此时P点与F点重合.
21. 放行准点率是衡量机场运行效率和服务质量的重要指标之一.某机场自2012年起采取相关策略优化各个服务环节,运行效率不断提升.以下是根据近10年年份数与该机场飞往A地航班放行准点率()(单位:百分比)的统计数据所作的散点图及经过初步处理后得到的一些统计量的值.
2017.5 80.4 1.5 40703145.0 1621254.2 277 12268
其中,
(1)根据散点图判断,与哪一个适宜作为该机场飞往A地航班放行准点率y关于年份数x的经验回归方程类型(给出判断即可,不必说明理由),并根据表中数据建立经验回归方程,由此预测2023年该机场飞往A地的航班放行准点率.
(2)已知2023年该机场飞往A地 B地和其他地区的航班比例分别为0.2、0.2和0.6.若以(1)中的预测值作为2023年该机场飞往A地航班放行准点率的估计值,且2023年该机场飞往B地及其他地区(不包含A、B两地)航班放行准点率的估计值分别为和,试解决以下问题:
(i)现从2023年在该机场起飞的航班中随机抽取一个,求该航班准点放行的概率;
(ii)若2023年某航班在该机场准点放行,判断该航班飞往A地、B地、其他地区等三种情况中的哪种情况的可能性最大,说明你的理由.
附:(1)对于一组数据,,…,,其回归直线的斜率和截距的最小二乘估计分别为,
参考数据:,,.
【答案】(1)适宜,预测2023年该机场飞往A地的航班放行准点率
(2)(i)0.778;(ii)可判断该航班飞往其他地区的可能性最大,理由见解析
【解析】
【分析】(1)根据线性回归方程的计算公式,选择合适的模型计算即可;
(2)利用全概率公式和条件概率公式,即可根据概率判断可能性最大的情况.
【小问1详解】
由散点图判断适宜作为该机场飞往A地航班放行准点率y关于年份数x的经验回归方程类型.
令,先建立y关于t的线性回归方程.
由于,
,
该机场飞往A地航班放行准点率y关于t的线性回归方程为,
因此y关于年份数x的回归方程为
所以当时,该机场飞往A地航班放行准点率y的预报值为
.
所以2023年该机场飞往A地航班放行准点率y的预报值为.
【小问2详解】
设“该航班飞往A地”,“该航班飞往B地”,“该航班飞往其他地区”,“该航班准点放行”,
则,,,
,,.
(i)由全概率公式得,
,
所以该航班准点放行的概率为0.778.
(ii),
,
,
因为,
所以可判断该航班飞往其他地区的可能性最大.
22. 已知函数有最大值,,且是 的导数.
(Ⅰ)求的值;
(Ⅱ)证明:当,时,.
【答案】(Ⅰ);(Ⅱ)见解析.
【解析】
【详解】试题分析:(Ⅰ)函数求导,讨论函数单调性求最值即可;
(Ⅱ)由(Ⅰ)可知,,求导得在上单调递增,由且得,由,单调递增,要证,即,只要证,即,所以只要证,构造函数求导证明即可.
试题解析:
(Ⅰ)的定义域为,.
当时,,
在上为单调递增函数,无最大值,不合题意,舍去;
当时,令,得,
当时,,函数单调递增;
当时,,函数单调递减,
,
,
.
(Ⅱ)由(Ⅰ)可知,,
.
,,
在上单调递增.
又,且,
.
,
当时,,单调递增,
要证,即,只要证,即.
,,
所以只要证 ————(*)
设 (其中),
,
在(0,1)上为增函数,
,故(*)式成立,从而.
同课章节目录
