12.2 三角形全等的判定(第2课时)初中数学人教版八年级上册课件(共18张PPT)
文档属性
| 名称 | 12.2 三角形全等的判定(第2课时)初中数学人教版八年级上册课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 129.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-05 23:08:05 | ||
图片预览





文档简介
(共18张PPT)
第十二章 全等三角形
12.2 三角形全等的判定
(第2课时)
八年级数学上册·人教版
旧知回顾
判断三角形 全等的方法:
1.定义(重合)法;
2.SSS.
先任意画出一个△ABC,再画一个△A/B/C/,使A/B/=AB,
∠A/ =∠A,A/C/ =AC.把画好的△A/B/C/剪下,放到△ABC上,它们全等吗?
探究
已知:任意 △ABC,画一个△ A/B/C/,
使A/B/=AB, ∠A/ =∠A, A/C/=AC:
画法:
1.画∠DA/ E=∠A;
2.在射线A/ D上截取A/B/=AB,在射线
A/ E上截取A/C/=AC;
3.连结B/C/.
△A/B/C/就是所要画的三角形.
问:通过实验可以发现什么事实?
探究反映的规律是:
两边和它们的夹角分别相等的
两个三角形能完全全等.
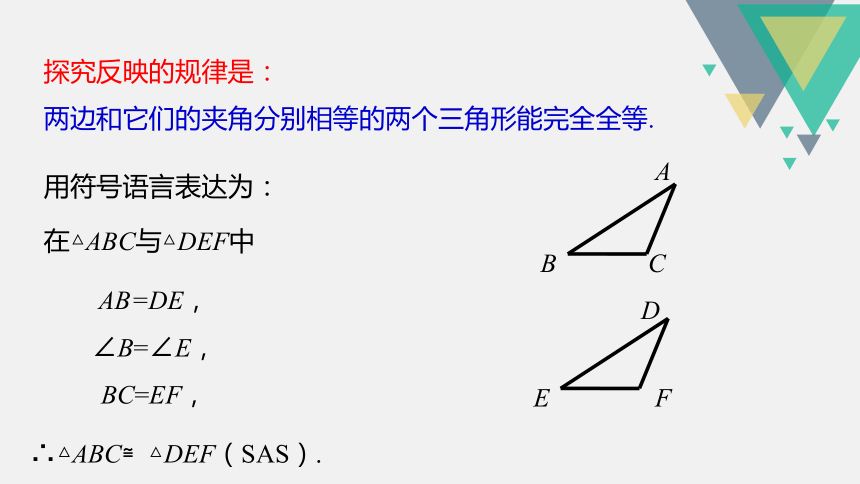
探究反映的规律是:
两边和它们的夹角分别相等的两个三角形能完全全等.
用符号语言表达为:
在△ABC与△DEF中
AB=DE,
∠B=∠E,
BC=EF,
∴△ABC≌△DEF(SAS).
A
B
C
D
E
F
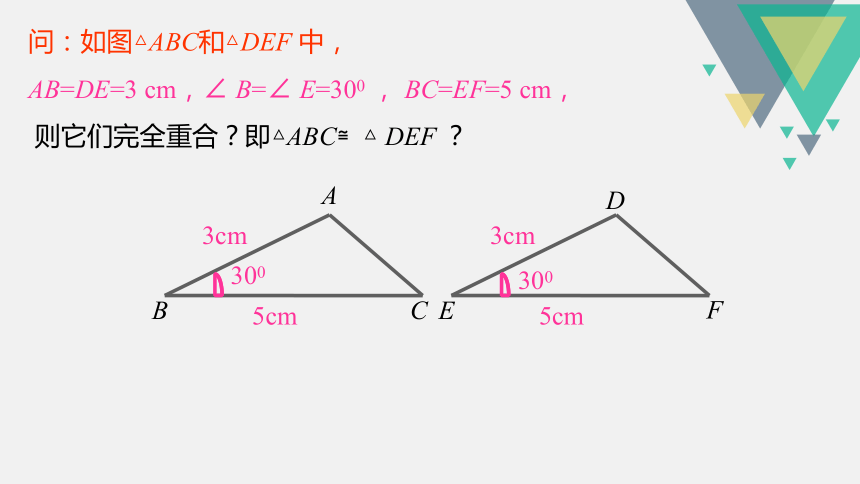
问:如图△ABC和△DEF 中,
AB=DE=3 cm,∠ B=∠ E=300 , BC=EF=5 cm,
则它们完全重合?即△ABC≌△ DEF ?
3cm
5cm
300
A
B
C
3cm
5cm
300
D
E
F
问:如图△ABC和△ DEF 中,
AB=DE=3 cm,∠ B=∠E= 300 , BC=EF=5 cm,
则它们完全重合?即△ABC≌△ DEF ?
3cm
5cm
300
A
B
C
3cm
5cm
300
D
E
F
练一练
分别找出各题中的全等三角形.
A
B
C
40°
40°
D
E
F
(1)
D
C
A
B
(2)
△ABC≌△EFD 根据“SAS”.
△ADC≌△CBA 根据“SAS”.
例题:已知:如图, AB=CB ,∠ABD= ∠CBD,
△ABD 和△ CBD 全等吗?
A
B
C
D
分析:
△ ABD ≌△ CBD
边:
角:
边:
AB=CB(已知),
∠ABD= ∠CBD(已知),
?
(SAS)
现在例1的已知条件不改变,而问题改变成:
问AD=CD,BD平分∠ADC吗?
解 :∵在ABD与△CBD中
AB=CB,
∠ABD=∠CBD,
BD=BD,
∴ △ABD≌△CBD(SAS).
已知:如图, AB=CB ,∠ABD= ∠CBD .
求证:AD=CD, BD 平分∠ADC.
A
B
C
D
证明: :∵在ABD与△CBD中
AB=CB,
∠ABD=∠CBD,
BD=BD,
∴ △ABD≌△CBD(SAS),
∴AD=CD (对应边相等),
∠ADB=∠CDB(对应角相等),
∴ BD平分∠ADC.
A
B
C
D
练习:已知:AD=CD, BD 平分∠ ADC .
问∠A=∠ C 吗?试证明.
证明:∵ BD 平分∠ADC,
∴ ∠ADB=∠BDC,
∵在△ADB与△DBC中
AD=CD,
∠ ADB=∠BDC,
BD=BD,
∴ △ABD≌△CBD(SAS),
∴ ∠A=∠C(对应角相等).
因铺设电线的需要,要在池塘两侧A、B处各埋设一根电线杆(如图),因无法直接量出A、B两点的距离,现有一足够的米尺.请你设计一种方案,粗略测出A、B两杆之间的距离.。
A
B
例题讲解
小明的设计方案:先在池塘旁取一个能直接到达A和B处的点C,连结AC并延长至D点,使AC=DC,连结BC并延长至E点,使BC=EC,连结ED,用米尺测出DE的长,这个长度就等于A,B两点的距离.请你说明理由.
解:∵在ACB与△DCE中
AC=DC ,
∠ACB=∠DCE,
BC=EC,
∴ △ACB≌△DCE (SAS),
∴ AB=DE.
A
B
C
D
E
练一练
以2.5cm,3.5cm为三角形的两边,长度为2.5cm的边所对的角为40° ,情况又怎样?动手画一画,你发现了什么?
A
B
C
D
E
F
2.5cm
3.5cm
40°
40°
3.5cm
2.5cm
结论:两边及其一边所对的角相等,两个三角形不一定全等.
课堂小结
l.利用全等三角形证明线段或角相等, 是证明线段或角相等的
重要方法之一,其思路如下:
⑴观察要证的线段和角在哪两个可能全等三角形之中.
⑵分析要证全等的这两个三角形,已知什么条件,还缺什么条件.
⑶设法证出所缺的条件.
课堂小结
2.利用全等三角形解决实际问题的步骤:
⑴根据实际抽象出几何图形.
⑵结合图形和题意写出已知,求证.
⑶写出证明过程.
本课结束
第十二章 全等三角形
12.2 三角形全等的判定
(第2课时)
八年级数学上册·人教版
旧知回顾
判断三角形 全等的方法:
1.定义(重合)法;
2.SSS.
先任意画出一个△ABC,再画一个△A/B/C/,使A/B/=AB,
∠A/ =∠A,A/C/ =AC.把画好的△A/B/C/剪下,放到△ABC上,它们全等吗?
探究
已知:任意 △ABC,画一个△ A/B/C/,
使A/B/=AB, ∠A/ =∠A, A/C/=AC:
画法:
1.画∠DA/ E=∠A;
2.在射线A/ D上截取A/B/=AB,在射线
A/ E上截取A/C/=AC;
3.连结B/C/.
△A/B/C/就是所要画的三角形.
问:通过实验可以发现什么事实?
探究反映的规律是:
两边和它们的夹角分别相等的
两个三角形能完全全等.
探究反映的规律是:
两边和它们的夹角分别相等的两个三角形能完全全等.
用符号语言表达为:
在△ABC与△DEF中
AB=DE,
∠B=∠E,
BC=EF,
∴△ABC≌△DEF(SAS).
A
B
C
D
E
F
问:如图△ABC和△DEF 中,
AB=DE=3 cm,∠ B=∠ E=300 , BC=EF=5 cm,
则它们完全重合?即△ABC≌△ DEF ?
3cm
5cm
300
A
B
C
3cm
5cm
300
D
E
F
问:如图△ABC和△ DEF 中,
AB=DE=3 cm,∠ B=∠E= 300 , BC=EF=5 cm,
则它们完全重合?即△ABC≌△ DEF ?
3cm
5cm
300
A
B
C
3cm
5cm
300
D
E
F
练一练
分别找出各题中的全等三角形.
A
B
C
40°
40°
D
E
F
(1)
D
C
A
B
(2)
△ABC≌△EFD 根据“SAS”.
△ADC≌△CBA 根据“SAS”.
例题:已知:如图, AB=CB ,∠ABD= ∠CBD,
△ABD 和△ CBD 全等吗?
A
B
C
D
分析:
△ ABD ≌△ CBD
边:
角:
边:
AB=CB(已知),
∠ABD= ∠CBD(已知),
?
(SAS)
现在例1的已知条件不改变,而问题改变成:
问AD=CD,BD平分∠ADC吗?
解 :∵在ABD与△CBD中
AB=CB,
∠ABD=∠CBD,
BD=BD,
∴ △ABD≌△CBD(SAS).
已知:如图, AB=CB ,∠ABD= ∠CBD .
求证:AD=CD, BD 平分∠ADC.
A
B
C
D
证明: :∵在ABD与△CBD中
AB=CB,
∠ABD=∠CBD,
BD=BD,
∴ △ABD≌△CBD(SAS),
∴AD=CD (对应边相等),
∠ADB=∠CDB(对应角相等),
∴ BD平分∠ADC.
A
B
C
D
练习:已知:AD=CD, BD 平分∠ ADC .
问∠A=∠ C 吗?试证明.
证明:∵ BD 平分∠ADC,
∴ ∠ADB=∠BDC,
∵在△ADB与△DBC中
AD=CD,
∠ ADB=∠BDC,
BD=BD,
∴ △ABD≌△CBD(SAS),
∴ ∠A=∠C(对应角相等).
因铺设电线的需要,要在池塘两侧A、B处各埋设一根电线杆(如图),因无法直接量出A、B两点的距离,现有一足够的米尺.请你设计一种方案,粗略测出A、B两杆之间的距离.。
A
B
例题讲解
小明的设计方案:先在池塘旁取一个能直接到达A和B处的点C,连结AC并延长至D点,使AC=DC,连结BC并延长至E点,使BC=EC,连结ED,用米尺测出DE的长,这个长度就等于A,B两点的距离.请你说明理由.
解:∵在ACB与△DCE中
AC=DC ,
∠ACB=∠DCE,
BC=EC,
∴ △ACB≌△DCE (SAS),
∴ AB=DE.
A
B
C
D
E
练一练
以2.5cm,3.5cm为三角形的两边,长度为2.5cm的边所对的角为40° ,情况又怎样?动手画一画,你发现了什么?
A
B
C
D
E
F
2.5cm
3.5cm
40°
40°
3.5cm
2.5cm
结论:两边及其一边所对的角相等,两个三角形不一定全等.
课堂小结
l.利用全等三角形证明线段或角相等, 是证明线段或角相等的
重要方法之一,其思路如下:
⑴观察要证的线段和角在哪两个可能全等三角形之中.
⑵分析要证全等的这两个三角形,已知什么条件,还缺什么条件.
⑶设法证出所缺的条件.
课堂小结
2.利用全等三角形解决实际问题的步骤:
⑴根据实际抽象出几何图形.
⑵结合图形和题意写出已知,求证.
⑶写出证明过程.
本课结束
