人教版数学八年级上册13.1.2 线段的垂直平分线的性质 课件 (共17张PPT)
文档属性
| 名称 | 人教版数学八年级上册13.1.2 线段的垂直平分线的性质 课件 (共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 314.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-06 07:54:18 | ||
图片预览




文档简介
(共17张PPT)
13.1.2 线段的垂直平分线的性质
第十三章 轴对称
八年级数学上册·人教版
知识回顾
沿一条直线折叠,这条直线的两
旁部分能够互相重合的图形叫
轴对称图形.
一个图形沿一条直线折叠,能
够与另一个图形重合,这两个
图形关于这条直线对称.
对称轴
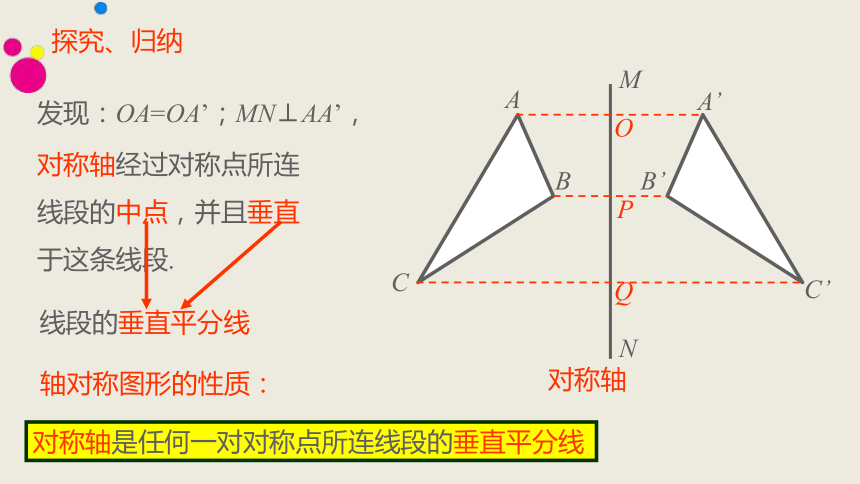
探究、归纳
发现:OA=OA’;MN⊥AA’,
对称轴
M
N
A
C
B
B’
A’
C’
O
P
Q
对称轴经过对称点所连
线段的中点,并且垂直
于这条线段.
线段的垂直平分线
轴对称图形的性质:
对称轴是任何一对对称点所连线段的垂直平分线
探究、归纳
如图:直线AC是线段BD的垂直平分线.
A
B
C
D
O
垂直平分线上的点到线段两端的距离相等
即:OB=OD,AC⊥BD.
发现:
AB=AD,
CB=CD,
P
PB=PD.
几何语言:
∵AC是BD的垂直平分线(或OB=OD,AC⊥BD).
∴AB=AD(或PB=PD).
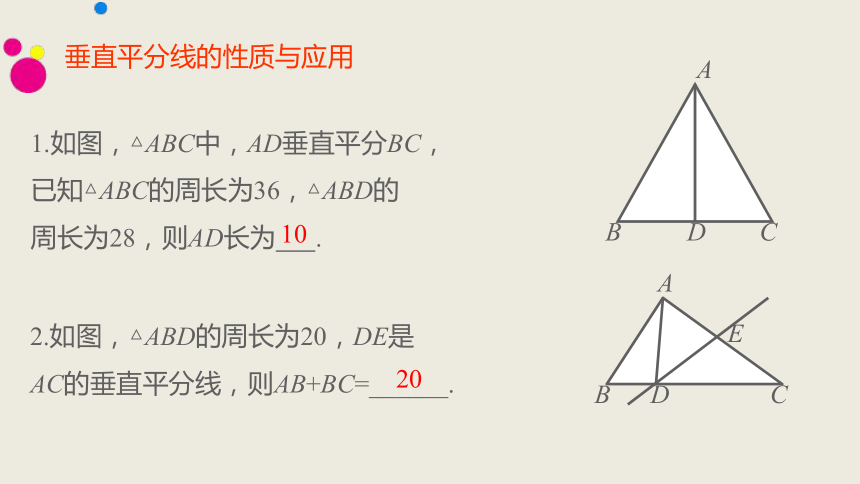
垂直平分线的性质与应用
1.如图,△ABC中,AD垂直平分BC,
已知△ABC的周长为36,△ABD的
周长为28,则AD长为 .
A
B
C
D
2.如图,△ABD的周长为20,DE是
AC的垂直平分线,则AB+BC=______.
A
B
C
D
E
10
20
3.如图,AD⊥BC,BD=CD,C在AE垂直平分线上.
(1)AB,AC,CE的长度有何关系?为什么?
(2)AB+BD与DE有何关系?为什么?
A
B
C
D
E
知识应用
(2)AB+BD=DE.∵ AB=CE,BD=CD,
∴AB+BD=CE+CD,∴AB+BD=DE.
解:(1)AB=AC=CE.理由如下:
∵ AD⊥BC,BD=CD,∴AB=AC,
又∵ C在AE垂直平分线上,∴AC=CE.
∴AB=AC=CE.
探究、归纳
已知如图:在△PAB中,PA=PB,那么点P在线段AB的垂直平分线上吗?
A
B
P
到线段两端的距离相等的点在线段的垂直平分线上
几何语言:
∵PA=PB,
∴点P在AB的垂直平分线上.
注意:经过点P的直线不一定是垂直平分线.
O
证明:过点P作△PAB的中线.
垂直平分线的性质与应用
1.下列说法错误的是( )
A.点D,E在线段AB垂直平分线上,则AD=BD,AE=BE
B.若AD=BD,AE=BE,则DE是线段AB的垂直平分线
C.若PA=PB,则点P在线段AB的垂直平分线上
D.若PA=PB,则过点P的直线是AB的垂直平分线
D
2.如图,AB=AC,MB=MC,直线AM是线段BC的垂直平分线吗?
知识应用
解:直线AM是线段BC的垂直平分线.
∵AB=AC,∴点A在线段BC的垂直平分线上,
理由:与一条线段两个端点距离相等的点,
在这条线段的垂直平分线上.
∵MB=MC,
∴点M在线段BC的垂直平分线上,
∴直线AM是线段BC的垂直平分线,
理由:两点确定一条直线.
3.利用圆规和直尺作已知线段的垂直平分线(独立完成,同位交流)
A
B
4.如图,△ABC中,DE是AC的垂直平分线,AE=3 ,△ABD的周长
为13 ,求△ABC的周长.
解:∵DE是AC的垂直平分线,
∴AD=CD, CE=AE.
∵AE=3 ,∴CE=AE=3. ∴AC=6 .
∵△ABD的周长为13 ,∴ AB+AD+BD=13 .
∴△ABC的周=AB+BC+AC=AB+BD+CD+AC=AB+BD+AD+AC
=13+6 =19 .
知识应用
知识应用
下图小河边有两个村庄,要在河边CD某处建一自来水厂向A村与B村供水,若要使厂部到A、B的距离相等,则应建在哪儿?
作法:连接AB,
作线段AB的垂直平分线l,交边CD于O点,O点就是自来水厂的地方.
课堂练习
1.如图,△ABC中,AB的垂直平分
线交AC于点D,若AC=5,BC=4,
则△BCD的周长= .
2.如图,AB比AC长2cm,DE垂直平分BC,
△ACD周长为14cm,则AB=_______,
AC=_______.
C
A
B
D
E
A
B
C
D
E
9
6cm
8cm
3.如图,有一块三角形田地,AB=AC=10m,作AB的垂直平分线ED交AC于D,交AB于E,量得△BDC的周长为17m,请你替测量人员计算BC的长.
解:因为ED是AB的垂直平分线,
所以AD=BD,
因为△BDC的周长为17m,
所以BD+CD+BC=17m,
所以AD+CD+BC=17m,
即AC+BC=17m,
因为AC=10m,
所以BC=17-10 =7 m.
4.如图,A,B,C三个村庄之间有三条公路,现在要建一个小型菜场P.
使得它到三条公路的距离相等
A
B
C
使得它到三个村庄的距离相等
作法:1.连接AB,BC,CA ;
2.作线段AB,线段BC的垂直平分线m、n,两直线交于点O,点O就是菜场P的位置.
通过这节课的学习,你有什么收获?
本课结束
13.1.2 线段的垂直平分线的性质
第十三章 轴对称
八年级数学上册·人教版
知识回顾
沿一条直线折叠,这条直线的两
旁部分能够互相重合的图形叫
轴对称图形.
一个图形沿一条直线折叠,能
够与另一个图形重合,这两个
图形关于这条直线对称.
对称轴
探究、归纳
发现:OA=OA’;MN⊥AA’,
对称轴
M
N
A
C
B
B’
A’
C’
O
P
Q
对称轴经过对称点所连
线段的中点,并且垂直
于这条线段.
线段的垂直平分线
轴对称图形的性质:
对称轴是任何一对对称点所连线段的垂直平分线
探究、归纳
如图:直线AC是线段BD的垂直平分线.
A
B
C
D
O
垂直平分线上的点到线段两端的距离相等
即:OB=OD,AC⊥BD.
发现:
AB=AD,
CB=CD,
P
PB=PD.
几何语言:
∵AC是BD的垂直平分线(或OB=OD,AC⊥BD).
∴AB=AD(或PB=PD).
垂直平分线的性质与应用
1.如图,△ABC中,AD垂直平分BC,
已知△ABC的周长为36,△ABD的
周长为28,则AD长为 .
A
B
C
D
2.如图,△ABD的周长为20,DE是
AC的垂直平分线,则AB+BC=______.
A
B
C
D
E
10
20
3.如图,AD⊥BC,BD=CD,C在AE垂直平分线上.
(1)AB,AC,CE的长度有何关系?为什么?
(2)AB+BD与DE有何关系?为什么?
A
B
C
D
E
知识应用
(2)AB+BD=DE.∵ AB=CE,BD=CD,
∴AB+BD=CE+CD,∴AB+BD=DE.
解:(1)AB=AC=CE.理由如下:
∵ AD⊥BC,BD=CD,∴AB=AC,
又∵ C在AE垂直平分线上,∴AC=CE.
∴AB=AC=CE.
探究、归纳
已知如图:在△PAB中,PA=PB,那么点P在线段AB的垂直平分线上吗?
A
B
P
到线段两端的距离相等的点在线段的垂直平分线上
几何语言:
∵PA=PB,
∴点P在AB的垂直平分线上.
注意:经过点P的直线不一定是垂直平分线.
O
证明:过点P作△PAB的中线.
垂直平分线的性质与应用
1.下列说法错误的是( )
A.点D,E在线段AB垂直平分线上,则AD=BD,AE=BE
B.若AD=BD,AE=BE,则DE是线段AB的垂直平分线
C.若PA=PB,则点P在线段AB的垂直平分线上
D.若PA=PB,则过点P的直线是AB的垂直平分线
D
2.如图,AB=AC,MB=MC,直线AM是线段BC的垂直平分线吗?
知识应用
解:直线AM是线段BC的垂直平分线.
∵AB=AC,∴点A在线段BC的垂直平分线上,
理由:与一条线段两个端点距离相等的点,
在这条线段的垂直平分线上.
∵MB=MC,
∴点M在线段BC的垂直平分线上,
∴直线AM是线段BC的垂直平分线,
理由:两点确定一条直线.
3.利用圆规和直尺作已知线段的垂直平分线(独立完成,同位交流)
A
B
4.如图,△ABC中,DE是AC的垂直平分线,AE=3 ,△ABD的周长
为13 ,求△ABC的周长.
解:∵DE是AC的垂直平分线,
∴AD=CD, CE=AE.
∵AE=3 ,∴CE=AE=3. ∴AC=6 .
∵△ABD的周长为13 ,∴ AB+AD+BD=13 .
∴△ABC的周=AB+BC+AC=AB+BD+CD+AC=AB+BD+AD+AC
=13+6 =19 .
知识应用
知识应用
下图小河边有两个村庄,要在河边CD某处建一自来水厂向A村与B村供水,若要使厂部到A、B的距离相等,则应建在哪儿?
作法:连接AB,
作线段AB的垂直平分线l,交边CD于O点,O点就是自来水厂的地方.
课堂练习
1.如图,△ABC中,AB的垂直平分
线交AC于点D,若AC=5,BC=4,
则△BCD的周长= .
2.如图,AB比AC长2cm,DE垂直平分BC,
△ACD周长为14cm,则AB=_______,
AC=_______.
C
A
B
D
E
A
B
C
D
E
9
6cm
8cm
3.如图,有一块三角形田地,AB=AC=10m,作AB的垂直平分线ED交AC于D,交AB于E,量得△BDC的周长为17m,请你替测量人员计算BC的长.
解:因为ED是AB的垂直平分线,
所以AD=BD,
因为△BDC的周长为17m,
所以BD+CD+BC=17m,
所以AD+CD+BC=17m,
即AC+BC=17m,
因为AC=10m,
所以BC=17-10 =7 m.
4.如图,A,B,C三个村庄之间有三条公路,现在要建一个小型菜场P.
使得它到三条公路的距离相等
A
B
C
使得它到三个村庄的距离相等
作法:1.连接AB,BC,CA ;
2.作线段AB,线段BC的垂直平分线m、n,两直线交于点O,点O就是菜场P的位置.
通过这节课的学习,你有什么收获?
本课结束
