人教版2023年九年级上册 第22章 二次函数 单元测试卷 (含解析)
文档属性
| 名称 | 人教版2023年九年级上册 第22章 二次函数 单元测试卷 (含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 527.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-06 10:25:11 | ||
图片预览



文档简介
人教版2023年九年级上册 第22章 二次函数 单元测试卷
一.选择题(共12小题,满分36分,每小题3分)
1.下列函数中是二次函数的是( )
A.y=﹣2x B.y=﹣ C.y=1﹣3x2 D.y=x+3
2.下列具有二次函数关系的是( )
A.正方形的周长y与边长x
B.速度一定时,路程s与时间t
C.正方形的面积y与边长x
D.三角形的高一定时,面积y与底边长x
3.抛物线y=(x﹣2)2﹣1的顶点坐标是( )
A.(﹣2,1) B.(﹣2,﹣1) C.(2,1) D.(2,﹣1)
4.抛物线y=x2+4x﹣5的对称轴为( )
A.y轴 B.x轴 C.直线x=2 D.直线x=﹣2
5.在同一坐标系中,一次函数y=﹣mx+1与二次函数y=x2+m的图象可能是( )
A. B. C. D.
6.抛物线y=x2+4x﹣c与x轴只有一个公共点,则c的值为( )
A.c=4 B.c=﹣4 C.c≤4 D.c≥﹣4
7.抛物线y=2(x+1)2﹣4平移后,得到抛物线,y=2x2,则平移方法是( )
A.先向左平移1个单位,再向上平移4个单位
B.先向左平移1个单位,再向7平移4个单位
C.先向右平移1个单位,再向上平移4个单位
D.先向右平移1个单位,再向下平移4个单位
8.抛物线y=a(x﹣2)2+k的开口向上,点A(﹣1,y1),B(3,y2)是抛物线上两点,则y1,y2的大小关系是( )
A.y1>y2 B.y1<y2 C.y1=y2 D.无法比较
9.已知二次函数y=x2﹣4x+2,当﹣1≤x≤1时,y的最小值为( )
A.﹣3 B.﹣2 C.﹣1 D.7
10.如图是一款抛物线型落地灯筒示意图,防滑螺母C为抛物线支架的最高点,灯罩D距离地面1.5米,最高点C距灯柱的水平距离为1.6米,灯柱AB=1.5米,若茶几摆放在灯罩的正下方,则茶几到灯柱的距离AE为多少米( )
A.3.2 B.0.32 C.2.5 D.1.6
11.已知函数,使y=a成立时x的值恰好只有3个,则a的值为( )
A.﹣2 B.0 C.1 D.2
12.二次函数y=ax2+bx+c(a≠0)图象如图,下列结论:
①abc>0;②2a+b=0;③当m≠1时,a+b>am2+bm;④a﹣b+c>0;⑤若+bx1=+bx2,且x1≠x2,则x1+x2=2.其中正确的有( )
A.①②③ B.①②④ C.③④⑤ D.②③⑤
二.填空题(共6小题,满分18分,每小题3分)
13.如果函数y=(m﹣3)x|m﹣1|+3x﹣1是二次函数,那么m的值为 .
14.抛物线在y轴的右侧呈 趋势(填“上升”或者“下降”).
15.函数y=kx2+x+1(k为常数)的图象与坐标轴有两个交点,则k的值为 .
16.某学校航模组设计制作的火箭升空高度h(m)与飞行时间t(s)满足函数关系式为h=﹣t2+14t+3,当火箭升空到最高点时,距离地面 m.
17.如图,已经二次函数y=ax2+bx+c(a<0)的图象如图所示,直线l∥x轴,则当ax2+bx+c≥1时x的取值范围 .
18.如图,函数的图象,若直线y=x+m与该图象只有一个交点,则m的取值范围为 .
三.解答题(共6小题,满分46分)
19.(6分)已知二次函数y=﹣2x2+4x+6.
(1)求该函数图象的顶点坐标、对称轴和与x轴的交点的坐标.
(2)自变量x在什么范围内,y随x的增大而增大?在什么范围内,y随x的增大而减小?
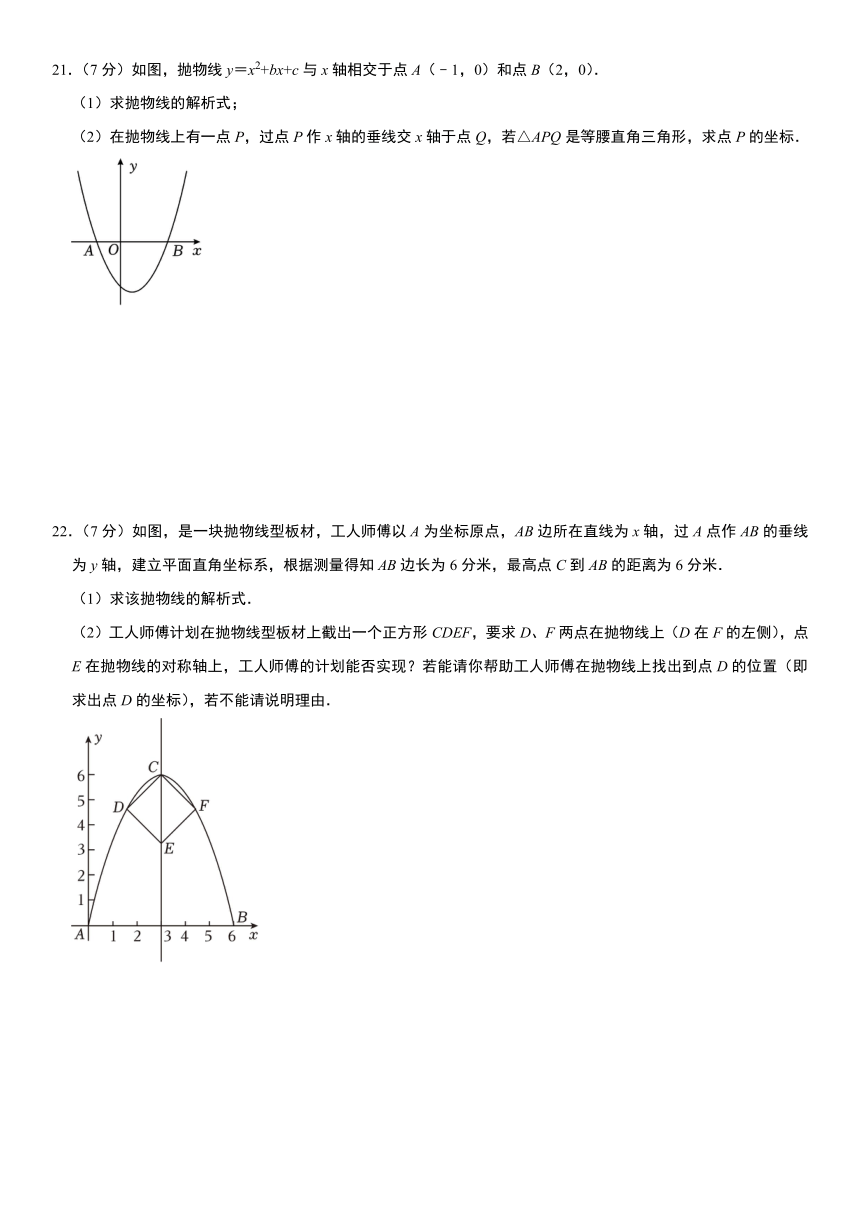
20.(8分)用描点法画函数的图象是学习各类函数的基础,并能直观反映出两个变量之间的函数关系.请用描点法画函数的图象,并按照要求回答下列问题:
x … ﹣3 ﹣2 ﹣1 0 1 2 3 …
y … 4.5 …
(1)在表格内填空;
(2)在所给坐标系内描点;
(3)用平滑曲线连线;
(4)由图象可知:当x=4时,y= ;当y<2时,x的取值范围是 .
21.(7分)如图,抛物线y=x2+bx+c与x轴相交于点A(﹣1,0)和点B(2,0).
(1)求抛物线的解析式;
(2)在抛物线上有一点P,过点P作x轴的垂线交x轴于点Q,若△APQ是等腰直角三角形,求点P的坐标.
22.(7分)如图,是一块抛物线型板材,工人师傅以A为坐标原点,AB边所在直线为x轴,过A点作AB的垂线为y轴,建立平面直角坐标系,根据测量得知AB边长为6分米,最高点C到AB的距离为6分米.
(1)求该抛物线的解析式.
(2)工人师傅计划在抛物线型板材上截出一个正方形CDEF,要求D、F两点在抛物线上(D在F的左侧),点E在抛物线的对称轴上,工人师傅的计划能否实现?若能请你帮助工人师傅在抛物线上找出到点D的位置(即求出点D的坐标),若不能请说明理由.
23.(8分)农户销售某农产品,经市场调查发现:若售价为6元/千克,日销售量为40千克,若售价每提高1元/千克,日销售量就减少2千克.现设售价为x元/千克(x≥6且为正整数).
(1)若某日销售量为24千克,求该日产品的单价;
(2)若政府将销售价格定为不超过18元/千克.设每日销售额为w元,求w关于x的函数表达式,并求w的最大值和最小值;
(3)市政府每日给农户补贴a元后(a为正整数),发现最大日收入(日收入=销售额+政府补贴)还是不超过450元,并且只有5种不同的单价使日收入不少于440元,请直接写出所有符合题意的a的值.
24.(10分)如图,在平面直角坐标系中,抛物线y=ax2+bx+3(a≠0)与x轴交于A(﹣3,0),B(1,0)两点,与y轴交于点C.
(1)求该抛物线的函数表达式;
(2)点P是直线AC上方抛物线上任意一点,过点P分别作y轴、x轴的平行线,交直线AC于点Q,R,求QR的最大值及此时点P的坐标;
(3)在(2)中QR取得最大值的条件下,将该抛物线向右平移个3个单位,点B平移后的对应点为D,E为新抛物线对称轴上任意一点,在新抛物线上确定一点F,使得以点P,D,E,F为顶点的四边形是平行四边形,直接写出所有符合条件的点F的坐标.
人教版九年级上册 第22章 二次函数 单元测试卷
参考答案与试题解析
一.选择题(共12小题,满分36分,每小题3分)
1.【解答】解:A、y=﹣2x,是正比例函数,不合题意;
B、y=﹣,是反比例函数,不合题意;
C、y=1﹣3x2,是二次函数,符合题意;
D、y=x+3,是一次函数,不合题意;
故选:C.
2.【解答】解:A、y=4x,是一次函数,错误;
B、s=vt,v一定,是一次函数,错误;
C、y=x2,是二次函数,正确;
D、y=hx,h一定,是一次函数,错误.
故选:C.
3.【解答】解:∵抛物线y=a(x﹣h)2+k的顶点坐标是(h,k),
∴抛物线y=(x﹣2)2﹣1的顶点坐标是(2,﹣1),
故选:D.
4.【解答】解:由题意可得,y=x2+4x﹣5的对称轴为:,
故选:D.
5.【解答】解:∵二次函数为y=x2+m,
∴a=1>0,
∴二次函数的开口方向向上,
∴排除C选项.
∵一次函数y=﹣mx+1,
∴b=1>0,
∵一次函数经过y轴正半轴,
∴排除A选项.
当m>0时,则﹣m<0,
一次函数经过一、二、四象限,
二次函数y=x2+m经过y轴正半轴,
∴排除B选项.
当m<0时,则﹣m>0
一次函数经过一、二、三象限,
二次函数y=x2+m经过y轴负半轴,
∴D选项符合题意.
故选:D.
6.【解答】解:∵抛物线y=x2+4x﹣c与x轴只有一个公共点,
∴方程x2+4x﹣c=0有两个相等的实数根,
∴Δ=b2﹣4ac=42﹣4×1 (﹣c)=0,
∴c=﹣4.
故选:B.
7.【解答】解:∵抛物线y=2(x+1)2﹣4的顶点坐标为(﹣1,﹣4),
平移后抛物线y=2x2的顶点坐标为(0,0),
∴平移方法为:向右平移1个单位,再向上平移4个单位.
故选:C.
8.【解答】解:∵抛物线y=a(x﹣2)2+k的图象与性质,确定抛物线开口向上,对称轴为x=2,
∴函数y=a(x﹣2)2+k可取到最小值,
∴抛物线上的点离对称轴越近,对应的函数值越小,
∵点A(﹣1,y1),B(3,y2)是抛物线上两点,A(﹣1,y1)到对称轴距离为2﹣(﹣1)=3,B(3,y2)到对称轴距离为3﹣2=1,1<3,
∴B(3,y2)到对称轴距离比A(﹣1,y1)到对称轴距离近,
∴y1>y2,
故选:A.
9.【解答】解:由题意得:二次函数的对称轴为直线,
∵a=1>0,
∴当x<2时,y随x的增大而减小,
∵﹣1≤x≤1,
∴当x=1时,二次函数y=x2﹣4x+2有最小值,即为:y=12﹣4×1+2=﹣1;
故选:C.
10.【解答】解:如图所示,以AE所在直线为x轴、AB所在直线为y轴建立平面直角坐标系,
方法一:∵AB=DE=1.5m,
∴点B与点D关于对称轴对称,
∴AE=2×1.6=3.2(m);
方法二:根据题意知,抛物线的顶点C的坐标为(1.6,2.5),
设抛物线的解析式为y=a(x﹣1.6)2+2.5,
将点B(0,1.5)代入得,2.56a+2.5=1.5,
解得a=﹣,
∴抛物线的解析式为y=﹣(x﹣1.6)2+2.5,
当y=1.5时,﹣(x﹣1.6)2+2.5=1.5,
解得x=0(舍)或x=3.2,
所以茶几到灯柱的距离AE为3.2米,
故选:A.
11.【解答】解:函数的图象如图:
根据图象知道当y=2时,对应成立的x值恰好有三个,
∴a=2.
故选:D.
12.【解答】解:∵抛物线开口向下,
∴a<0,
∵抛物线的对称轴为直线x=﹣=1,
∴b=﹣2a>0,
∵抛物线与y轴的交点在y轴的正半轴,
∴c>0,
∴abc<0,所以①错误;
∵b=﹣2a,
∴2a+b=0,所以②正确;
∵抛物线的对称轴为直线x=1,抛物线开口向下,
∴当x=1时,y有最大值,
∴当m≠1时,a+b+c>am2+bm+c,
即当m≠1时,a+b>am2+bm,所以③正确;
∵抛物线的对称轴为直线x=1,抛物线与x轴的一个交点在点(3,0)的左侧,
∴抛物线与x轴的另一个交点在(﹣1,0)的右侧,
∴x=﹣1时,y<0,
即a﹣b+c<0,所以④错误;
若+bx1=+bx2,且x1≠x2,
即若+bx1+c=+bx2+c,且x1≠x2,则x1+x2=2.
∴x=x1和x=x2时,函数值相等,
∴x1﹣1=1﹣x2,
∴x1+x2=2,所以⑤正确.
故选:D.
二.填空题(共6小题,满分18分,每小题3分)
13.【解答】解:∵函数y=(m﹣3)x|m﹣1|+3x﹣1是二次函数,
∴|m﹣1|=2,且m﹣3≠0,
解得:m=﹣1.
故答案为:﹣1.
14.【解答】解:∵中的a=﹣<0,b=0,
∴抛物线开口向下,对称轴为y轴,
∴y轴右侧部分下降,
故答案为:下降.
15.【解答】解:∵函数y=kx2+x+1(k为常数)的图象与坐标轴有两个交点,
①二次函数图象与x轴有1个交点,
∴1﹣4k=0,
∴k=,
②一次函数图象与坐标轴有两个交点,
∴k=0,
∴k的值为0或,
故答案为:0或.
16.【解答】解:由题意可得:h=﹣t2+14t+3=﹣(t2﹣14t)+3=﹣(t﹣7)2+52,
∵a=﹣1<0,
∴抛物线开口向下,
当x=7时,h取得最大值,当火箭升空到最高点时,距离地面52m.
故答案为:52.
17.【解答】解:由函数图象可知抛物线对称轴为直线x=1,直线l与抛物线交于点(2.5,1),
∴直线l与抛物线的另一个交点坐标为(﹣0.5,1).
∴当﹣0.5≤x≤2.5时,ax2+bx+c≥1,
故答案为:﹣0.5≤x≤2.5.
18.【解答】解:由题意,直线y=x+m与函数y=的图象恒相交,
①当m>0时,直线y=x+m与直线y=﹣x(x<0)恒相交,与抛物线y=﹣x2+2x(x>0)至少有一个交点时,即方程x+m=﹣x2+2x(x>0)有两个实数根,
∴x2﹣x+m=0,
∴Δ=(﹣1)2﹣4×1×m≥0,
解得:;
∴当时,直线y=x+m与函数y=的图象有两个或三个交点,
∴当时,直线y=x+m与函数y=的图象只有一个交点;
②当m≤0时,由图象可知,直线y=x+m与函数y=的图象只有一个交点,
综上,若直线y=x+m与该图象只有一个交点,则m的取值范围为或m≤0.
故答案为:或m≤0.
三.解答题(共6小题,满分46分)
19.【解答】解:(1)∵y=﹣2x2+4x+6=﹣2(x﹣1)2+8,
∴抛物线的对称轴为直线x=1,顶点坐标为(1,8),
取y=0,则﹣2(x﹣1)2+8=0,
解得x=﹣1或x=3,
∴抛物线与x轴的交点为(﹣1,0)和(3,0);
(2)∵抛物线的二次项系数小于0,
∴抛物线的开口向下,
又∵抛物线的对称轴为直线x=1,
∴当x>1时,y随着x的增大而减小,
当x<1时,y随着x的增大而增大.
20.【解答】解:(1)当x=﹣2时,y=×(﹣2)2=2;
当x=﹣1时,y=×(﹣1)2=0.5;
当x=0时,y=0;
当x=1时,y=×12=0.5;
当x=2时,y=×22=2;
当x=3时,y=×32=4.5.
故答案为:2,0.5,0,0.5,2,4.5.
(2)描点如图.
(3)用平滑曲线连线如上图.
(4)由图象可知:
当x=4时,y=8;
当y<2时,﹣2<x<2.
故答案为:8,﹣2<x<2.
21.【解答】解:(1)∵抛物线y=x2+bx+c与x轴相交于点A(﹣1,0)和点B(2,0).
∴,
解得,,
∴抛物线的解析式为y=x2﹣x﹣2.
(2)如图,∵PQ⊥x轴于Q,
∴∠PQA=90°,
∵△APQ是等腰直角三角形,
∴AQ=PQ,
∵点P在抛物线y=x2﹣x﹣2上,
∴设点Q的坐标为(m,0)则点P(m,m2﹣m﹣2),
∴AQ=|m﹣(﹣1)|=|m+1|,PQ=|m2﹣m﹣2|,
∴|m+1|=|m2﹣m﹣2|,
∴m+1=m2﹣m﹣2或m+1=﹣(m2﹣m﹣2),
即m2﹣2m﹣3=0或m2=1,
当m2﹣2m﹣3=0时,
解得,m=3或m=﹣1(舍去),
此时P(3,4),
当m2=1时,
解得,m=1或m=﹣1(舍去),
此时P(1,﹣2),
综上得,点P的坐标为P(3,4)或(1,2).
22.【解答】解:(1)∵AB边长为6分米,最高点C到AB的距离为6分米.
∴点B的坐标为(6,0),
根据抛物线的对称性可知:顶点C的坐标为(3,6),
设这个抛物线的解析式为:y=a(x﹣3)2+6,
将点(6,0)代入y=a(x﹣3)2+6,得:0=a(6﹣3)2+6,解得:,
∴抛物线的解析式为:,
(2)能够实现,点D的坐标为:(1.5,4.5).
∵点D在抛物线上,
∴可设点D的坐标为,
连接DF交CE于点H,如图:
∵四边形CDEF为正方形,
∴HD=HC,DF⊥CE,
∵CE为抛物线的对称轴,点C的坐标为(3,6),
∴点H的坐标为,
∴HD=3﹣t,,
∴,
整理得:2t2﹣9t+9=0,
解得:t=1.5或t=3(不合题意,舍去),
当t=1.5时,,
∴点D的坐标为(1.5,4.5).
23.【解答】解(1)售价为x元/千克(x≥6且为正整数),则提价(x﹣6)元,
故销售量为[40﹣2(x﹣6)]=(52﹣2x)千克,
根据题意,得52﹣2x=24,
解得x=14,
故该日产品的单价为14元/千克.
(2)设售价为x元/千克(x≥6且为正整数),销售额为w元,则提价(x﹣6)元,
故销售量为[40﹣2(x﹣6)]=(52﹣2x)千克,
∴w=x(52﹣2x)=﹣2x2+52x,
∴w=﹣2(x﹣13)2+338,
∵6≤x≤18,且对称轴右侧,y随x的增大而减小,到对称轴距离越大,函数值越小,且13﹣6=7,18﹣13=5,
∴x=13时,w取得最大值,且最大值为338元,
∴x=6时,w取得最小值,且最小值为240元,
w=﹣2x2+52x,w的最大338元,w的最小240元.
(3)由题意得:440≤﹣2x2+52x+a≤450,由二次函数的对称性可知x的取值为11,12,13,14,15,
∴x=13时,w=338元
∴x=11或15时,w=330元,
∴x=12或14时,w=336元,
且:440≤﹣2x2+52x+a≤450,
∴110≤a≤112,
∵a是正整数,
∴a的值为110或111或112.
24.【解答】解:(1)∵抛物线与x轴交于A(﹣3,0),B(1,0)两点,
∴,
解得:,
∴该抛物线的函数表达式为y=﹣x2﹣2x+3;
(2)如图,PQ∥y轴,PR∥x轴,
在y=﹣x2﹣2x+3中,令x=0,得y=3.
∴点C的坐标为(0,3),
∴OC=3,
∵A(﹣3,0),
∴OA=3,
∴OA=OC,
∴△OAC为等腰直角三角形,
∴∠CAO=45°.
设直线AC的表达式为y=kx+m(k≠0),
∵A(﹣3,0),C(0,3),
∴,
解得:,
∴直线AC的表达式为y=x+3,
∵PR∥x轴,
∴∠PRQ=∠COA=45°.
又∵PQ∥y轴,
∴△PQR为等腰直角三角形,
∴QR2=PQ2+PR2=2PQ2,
即.
设点P的坐标为(t,﹣t2﹣2t+3)(其中﹣3<t<0),则点Q(t,t+3),
∴PQ=﹣t2﹣2t+3﹣(t+3)=﹣t2﹣3t=﹣(t+)2+.
∵﹣1<0,
∴当时,PQ有最大值.
∴QR的最大值为.
此时,点P的坐标为;
(3)由题意得:将抛物线y=﹣x2﹣2x+3向右平移3个单位后的新抛物线解析式为y=﹣(x﹣2)2+4=﹣x2+4x,点B(1,0)平移后的对应点为D(4,0),
∵新抛物线y=﹣(x﹣2)2+4的对称轴为直线x=2,
∴设E(2,m),F(n,﹣n2+4n),
由(2)知P,
分情况讨论:
①当PF、DE为对角线时,则﹣+n=2+4,
解得:n=,
∴F1(,﹣);
②当DF、EP为对角线时,n+4=﹣+2,
解得:n=﹣,
∴F2(﹣,﹣);
③当EF、DP为对角线时,n+2=﹣+4,
解得:n=,
∴F3(,);
综上所述,点F的坐标为:F1(,﹣),F2(﹣,﹣),F3(,).
一.选择题(共12小题,满分36分,每小题3分)
1.下列函数中是二次函数的是( )
A.y=﹣2x B.y=﹣ C.y=1﹣3x2 D.y=x+3
2.下列具有二次函数关系的是( )
A.正方形的周长y与边长x
B.速度一定时,路程s与时间t
C.正方形的面积y与边长x
D.三角形的高一定时,面积y与底边长x
3.抛物线y=(x﹣2)2﹣1的顶点坐标是( )
A.(﹣2,1) B.(﹣2,﹣1) C.(2,1) D.(2,﹣1)
4.抛物线y=x2+4x﹣5的对称轴为( )
A.y轴 B.x轴 C.直线x=2 D.直线x=﹣2
5.在同一坐标系中,一次函数y=﹣mx+1与二次函数y=x2+m的图象可能是( )
A. B. C. D.
6.抛物线y=x2+4x﹣c与x轴只有一个公共点,则c的值为( )
A.c=4 B.c=﹣4 C.c≤4 D.c≥﹣4
7.抛物线y=2(x+1)2﹣4平移后,得到抛物线,y=2x2,则平移方法是( )
A.先向左平移1个单位,再向上平移4个单位
B.先向左平移1个单位,再向7平移4个单位
C.先向右平移1个单位,再向上平移4个单位
D.先向右平移1个单位,再向下平移4个单位
8.抛物线y=a(x﹣2)2+k的开口向上,点A(﹣1,y1),B(3,y2)是抛物线上两点,则y1,y2的大小关系是( )
A.y1>y2 B.y1<y2 C.y1=y2 D.无法比较
9.已知二次函数y=x2﹣4x+2,当﹣1≤x≤1时,y的最小值为( )
A.﹣3 B.﹣2 C.﹣1 D.7
10.如图是一款抛物线型落地灯筒示意图,防滑螺母C为抛物线支架的最高点,灯罩D距离地面1.5米,最高点C距灯柱的水平距离为1.6米,灯柱AB=1.5米,若茶几摆放在灯罩的正下方,则茶几到灯柱的距离AE为多少米( )
A.3.2 B.0.32 C.2.5 D.1.6
11.已知函数,使y=a成立时x的值恰好只有3个,则a的值为( )
A.﹣2 B.0 C.1 D.2
12.二次函数y=ax2+bx+c(a≠0)图象如图,下列结论:
①abc>0;②2a+b=0;③当m≠1时,a+b>am2+bm;④a﹣b+c>0;⑤若+bx1=+bx2,且x1≠x2,则x1+x2=2.其中正确的有( )
A.①②③ B.①②④ C.③④⑤ D.②③⑤
二.填空题(共6小题,满分18分,每小题3分)
13.如果函数y=(m﹣3)x|m﹣1|+3x﹣1是二次函数,那么m的值为 .
14.抛物线在y轴的右侧呈 趋势(填“上升”或者“下降”).
15.函数y=kx2+x+1(k为常数)的图象与坐标轴有两个交点,则k的值为 .
16.某学校航模组设计制作的火箭升空高度h(m)与飞行时间t(s)满足函数关系式为h=﹣t2+14t+3,当火箭升空到最高点时,距离地面 m.
17.如图,已经二次函数y=ax2+bx+c(a<0)的图象如图所示,直线l∥x轴,则当ax2+bx+c≥1时x的取值范围 .
18.如图,函数的图象,若直线y=x+m与该图象只有一个交点,则m的取值范围为 .
三.解答题(共6小题,满分46分)
19.(6分)已知二次函数y=﹣2x2+4x+6.
(1)求该函数图象的顶点坐标、对称轴和与x轴的交点的坐标.
(2)自变量x在什么范围内,y随x的增大而增大?在什么范围内,y随x的增大而减小?
20.(8分)用描点法画函数的图象是学习各类函数的基础,并能直观反映出两个变量之间的函数关系.请用描点法画函数的图象,并按照要求回答下列问题:
x … ﹣3 ﹣2 ﹣1 0 1 2 3 …
y … 4.5 …
(1)在表格内填空;
(2)在所给坐标系内描点;
(3)用平滑曲线连线;
(4)由图象可知:当x=4时,y= ;当y<2时,x的取值范围是 .
21.(7分)如图,抛物线y=x2+bx+c与x轴相交于点A(﹣1,0)和点B(2,0).
(1)求抛物线的解析式;
(2)在抛物线上有一点P,过点P作x轴的垂线交x轴于点Q,若△APQ是等腰直角三角形,求点P的坐标.
22.(7分)如图,是一块抛物线型板材,工人师傅以A为坐标原点,AB边所在直线为x轴,过A点作AB的垂线为y轴,建立平面直角坐标系,根据测量得知AB边长为6分米,最高点C到AB的距离为6分米.
(1)求该抛物线的解析式.
(2)工人师傅计划在抛物线型板材上截出一个正方形CDEF,要求D、F两点在抛物线上(D在F的左侧),点E在抛物线的对称轴上,工人师傅的计划能否实现?若能请你帮助工人师傅在抛物线上找出到点D的位置(即求出点D的坐标),若不能请说明理由.
23.(8分)农户销售某农产品,经市场调查发现:若售价为6元/千克,日销售量为40千克,若售价每提高1元/千克,日销售量就减少2千克.现设售价为x元/千克(x≥6且为正整数).
(1)若某日销售量为24千克,求该日产品的单价;
(2)若政府将销售价格定为不超过18元/千克.设每日销售额为w元,求w关于x的函数表达式,并求w的最大值和最小值;
(3)市政府每日给农户补贴a元后(a为正整数),发现最大日收入(日收入=销售额+政府补贴)还是不超过450元,并且只有5种不同的单价使日收入不少于440元,请直接写出所有符合题意的a的值.
24.(10分)如图,在平面直角坐标系中,抛物线y=ax2+bx+3(a≠0)与x轴交于A(﹣3,0),B(1,0)两点,与y轴交于点C.
(1)求该抛物线的函数表达式;
(2)点P是直线AC上方抛物线上任意一点,过点P分别作y轴、x轴的平行线,交直线AC于点Q,R,求QR的最大值及此时点P的坐标;
(3)在(2)中QR取得最大值的条件下,将该抛物线向右平移个3个单位,点B平移后的对应点为D,E为新抛物线对称轴上任意一点,在新抛物线上确定一点F,使得以点P,D,E,F为顶点的四边形是平行四边形,直接写出所有符合条件的点F的坐标.
人教版九年级上册 第22章 二次函数 单元测试卷
参考答案与试题解析
一.选择题(共12小题,满分36分,每小题3分)
1.【解答】解:A、y=﹣2x,是正比例函数,不合题意;
B、y=﹣,是反比例函数,不合题意;
C、y=1﹣3x2,是二次函数,符合题意;
D、y=x+3,是一次函数,不合题意;
故选:C.
2.【解答】解:A、y=4x,是一次函数,错误;
B、s=vt,v一定,是一次函数,错误;
C、y=x2,是二次函数,正确;
D、y=hx,h一定,是一次函数,错误.
故选:C.
3.【解答】解:∵抛物线y=a(x﹣h)2+k的顶点坐标是(h,k),
∴抛物线y=(x﹣2)2﹣1的顶点坐标是(2,﹣1),
故选:D.
4.【解答】解:由题意可得,y=x2+4x﹣5的对称轴为:,
故选:D.
5.【解答】解:∵二次函数为y=x2+m,
∴a=1>0,
∴二次函数的开口方向向上,
∴排除C选项.
∵一次函数y=﹣mx+1,
∴b=1>0,
∵一次函数经过y轴正半轴,
∴排除A选项.
当m>0时,则﹣m<0,
一次函数经过一、二、四象限,
二次函数y=x2+m经过y轴正半轴,
∴排除B选项.
当m<0时,则﹣m>0
一次函数经过一、二、三象限,
二次函数y=x2+m经过y轴负半轴,
∴D选项符合题意.
故选:D.
6.【解答】解:∵抛物线y=x2+4x﹣c与x轴只有一个公共点,
∴方程x2+4x﹣c=0有两个相等的实数根,
∴Δ=b2﹣4ac=42﹣4×1 (﹣c)=0,
∴c=﹣4.
故选:B.
7.【解答】解:∵抛物线y=2(x+1)2﹣4的顶点坐标为(﹣1,﹣4),
平移后抛物线y=2x2的顶点坐标为(0,0),
∴平移方法为:向右平移1个单位,再向上平移4个单位.
故选:C.
8.【解答】解:∵抛物线y=a(x﹣2)2+k的图象与性质,确定抛物线开口向上,对称轴为x=2,
∴函数y=a(x﹣2)2+k可取到最小值,
∴抛物线上的点离对称轴越近,对应的函数值越小,
∵点A(﹣1,y1),B(3,y2)是抛物线上两点,A(﹣1,y1)到对称轴距离为2﹣(﹣1)=3,B(3,y2)到对称轴距离为3﹣2=1,1<3,
∴B(3,y2)到对称轴距离比A(﹣1,y1)到对称轴距离近,
∴y1>y2,
故选:A.
9.【解答】解:由题意得:二次函数的对称轴为直线,
∵a=1>0,
∴当x<2时,y随x的增大而减小,
∵﹣1≤x≤1,
∴当x=1时,二次函数y=x2﹣4x+2有最小值,即为:y=12﹣4×1+2=﹣1;
故选:C.
10.【解答】解:如图所示,以AE所在直线为x轴、AB所在直线为y轴建立平面直角坐标系,
方法一:∵AB=DE=1.5m,
∴点B与点D关于对称轴对称,
∴AE=2×1.6=3.2(m);
方法二:根据题意知,抛物线的顶点C的坐标为(1.6,2.5),
设抛物线的解析式为y=a(x﹣1.6)2+2.5,
将点B(0,1.5)代入得,2.56a+2.5=1.5,
解得a=﹣,
∴抛物线的解析式为y=﹣(x﹣1.6)2+2.5,
当y=1.5时,﹣(x﹣1.6)2+2.5=1.5,
解得x=0(舍)或x=3.2,
所以茶几到灯柱的距离AE为3.2米,
故选:A.
11.【解答】解:函数的图象如图:
根据图象知道当y=2时,对应成立的x值恰好有三个,
∴a=2.
故选:D.
12.【解答】解:∵抛物线开口向下,
∴a<0,
∵抛物线的对称轴为直线x=﹣=1,
∴b=﹣2a>0,
∵抛物线与y轴的交点在y轴的正半轴,
∴c>0,
∴abc<0,所以①错误;
∵b=﹣2a,
∴2a+b=0,所以②正确;
∵抛物线的对称轴为直线x=1,抛物线开口向下,
∴当x=1时,y有最大值,
∴当m≠1时,a+b+c>am2+bm+c,
即当m≠1时,a+b>am2+bm,所以③正确;
∵抛物线的对称轴为直线x=1,抛物线与x轴的一个交点在点(3,0)的左侧,
∴抛物线与x轴的另一个交点在(﹣1,0)的右侧,
∴x=﹣1时,y<0,
即a﹣b+c<0,所以④错误;
若+bx1=+bx2,且x1≠x2,
即若+bx1+c=+bx2+c,且x1≠x2,则x1+x2=2.
∴x=x1和x=x2时,函数值相等,
∴x1﹣1=1﹣x2,
∴x1+x2=2,所以⑤正确.
故选:D.
二.填空题(共6小题,满分18分,每小题3分)
13.【解答】解:∵函数y=(m﹣3)x|m﹣1|+3x﹣1是二次函数,
∴|m﹣1|=2,且m﹣3≠0,
解得:m=﹣1.
故答案为:﹣1.
14.【解答】解:∵中的a=﹣<0,b=0,
∴抛物线开口向下,对称轴为y轴,
∴y轴右侧部分下降,
故答案为:下降.
15.【解答】解:∵函数y=kx2+x+1(k为常数)的图象与坐标轴有两个交点,
①二次函数图象与x轴有1个交点,
∴1﹣4k=0,
∴k=,
②一次函数图象与坐标轴有两个交点,
∴k=0,
∴k的值为0或,
故答案为:0或.
16.【解答】解:由题意可得:h=﹣t2+14t+3=﹣(t2﹣14t)+3=﹣(t﹣7)2+52,
∵a=﹣1<0,
∴抛物线开口向下,
当x=7时,h取得最大值,当火箭升空到最高点时,距离地面52m.
故答案为:52.
17.【解答】解:由函数图象可知抛物线对称轴为直线x=1,直线l与抛物线交于点(2.5,1),
∴直线l与抛物线的另一个交点坐标为(﹣0.5,1).
∴当﹣0.5≤x≤2.5时,ax2+bx+c≥1,
故答案为:﹣0.5≤x≤2.5.
18.【解答】解:由题意,直线y=x+m与函数y=的图象恒相交,
①当m>0时,直线y=x+m与直线y=﹣x(x<0)恒相交,与抛物线y=﹣x2+2x(x>0)至少有一个交点时,即方程x+m=﹣x2+2x(x>0)有两个实数根,
∴x2﹣x+m=0,
∴Δ=(﹣1)2﹣4×1×m≥0,
解得:;
∴当时,直线y=x+m与函数y=的图象有两个或三个交点,
∴当时,直线y=x+m与函数y=的图象只有一个交点;
②当m≤0时,由图象可知,直线y=x+m与函数y=的图象只有一个交点,
综上,若直线y=x+m与该图象只有一个交点,则m的取值范围为或m≤0.
故答案为:或m≤0.
三.解答题(共6小题,满分46分)
19.【解答】解:(1)∵y=﹣2x2+4x+6=﹣2(x﹣1)2+8,
∴抛物线的对称轴为直线x=1,顶点坐标为(1,8),
取y=0,则﹣2(x﹣1)2+8=0,
解得x=﹣1或x=3,
∴抛物线与x轴的交点为(﹣1,0)和(3,0);
(2)∵抛物线的二次项系数小于0,
∴抛物线的开口向下,
又∵抛物线的对称轴为直线x=1,
∴当x>1时,y随着x的增大而减小,
当x<1时,y随着x的增大而增大.
20.【解答】解:(1)当x=﹣2时,y=×(﹣2)2=2;
当x=﹣1时,y=×(﹣1)2=0.5;
当x=0时,y=0;
当x=1时,y=×12=0.5;
当x=2时,y=×22=2;
当x=3时,y=×32=4.5.
故答案为:2,0.5,0,0.5,2,4.5.
(2)描点如图.
(3)用平滑曲线连线如上图.
(4)由图象可知:
当x=4时,y=8;
当y<2时,﹣2<x<2.
故答案为:8,﹣2<x<2.
21.【解答】解:(1)∵抛物线y=x2+bx+c与x轴相交于点A(﹣1,0)和点B(2,0).
∴,
解得,,
∴抛物线的解析式为y=x2﹣x﹣2.
(2)如图,∵PQ⊥x轴于Q,
∴∠PQA=90°,
∵△APQ是等腰直角三角形,
∴AQ=PQ,
∵点P在抛物线y=x2﹣x﹣2上,
∴设点Q的坐标为(m,0)则点P(m,m2﹣m﹣2),
∴AQ=|m﹣(﹣1)|=|m+1|,PQ=|m2﹣m﹣2|,
∴|m+1|=|m2﹣m﹣2|,
∴m+1=m2﹣m﹣2或m+1=﹣(m2﹣m﹣2),
即m2﹣2m﹣3=0或m2=1,
当m2﹣2m﹣3=0时,
解得,m=3或m=﹣1(舍去),
此时P(3,4),
当m2=1时,
解得,m=1或m=﹣1(舍去),
此时P(1,﹣2),
综上得,点P的坐标为P(3,4)或(1,2).
22.【解答】解:(1)∵AB边长为6分米,最高点C到AB的距离为6分米.
∴点B的坐标为(6,0),
根据抛物线的对称性可知:顶点C的坐标为(3,6),
设这个抛物线的解析式为:y=a(x﹣3)2+6,
将点(6,0)代入y=a(x﹣3)2+6,得:0=a(6﹣3)2+6,解得:,
∴抛物线的解析式为:,
(2)能够实现,点D的坐标为:(1.5,4.5).
∵点D在抛物线上,
∴可设点D的坐标为,
连接DF交CE于点H,如图:
∵四边形CDEF为正方形,
∴HD=HC,DF⊥CE,
∵CE为抛物线的对称轴,点C的坐标为(3,6),
∴点H的坐标为,
∴HD=3﹣t,,
∴,
整理得:2t2﹣9t+9=0,
解得:t=1.5或t=3(不合题意,舍去),
当t=1.5时,,
∴点D的坐标为(1.5,4.5).
23.【解答】解(1)售价为x元/千克(x≥6且为正整数),则提价(x﹣6)元,
故销售量为[40﹣2(x﹣6)]=(52﹣2x)千克,
根据题意,得52﹣2x=24,
解得x=14,
故该日产品的单价为14元/千克.
(2)设售价为x元/千克(x≥6且为正整数),销售额为w元,则提价(x﹣6)元,
故销售量为[40﹣2(x﹣6)]=(52﹣2x)千克,
∴w=x(52﹣2x)=﹣2x2+52x,
∴w=﹣2(x﹣13)2+338,
∵6≤x≤18,且对称轴右侧,y随x的增大而减小,到对称轴距离越大,函数值越小,且13﹣6=7,18﹣13=5,
∴x=13时,w取得最大值,且最大值为338元,
∴x=6时,w取得最小值,且最小值为240元,
w=﹣2x2+52x,w的最大338元,w的最小240元.
(3)由题意得:440≤﹣2x2+52x+a≤450,由二次函数的对称性可知x的取值为11,12,13,14,15,
∴x=13时,w=338元
∴x=11或15时,w=330元,
∴x=12或14时,w=336元,
且:440≤﹣2x2+52x+a≤450,
∴110≤a≤112,
∵a是正整数,
∴a的值为110或111或112.
24.【解答】解:(1)∵抛物线与x轴交于A(﹣3,0),B(1,0)两点,
∴,
解得:,
∴该抛物线的函数表达式为y=﹣x2﹣2x+3;
(2)如图,PQ∥y轴,PR∥x轴,
在y=﹣x2﹣2x+3中,令x=0,得y=3.
∴点C的坐标为(0,3),
∴OC=3,
∵A(﹣3,0),
∴OA=3,
∴OA=OC,
∴△OAC为等腰直角三角形,
∴∠CAO=45°.
设直线AC的表达式为y=kx+m(k≠0),
∵A(﹣3,0),C(0,3),
∴,
解得:,
∴直线AC的表达式为y=x+3,
∵PR∥x轴,
∴∠PRQ=∠COA=45°.
又∵PQ∥y轴,
∴△PQR为等腰直角三角形,
∴QR2=PQ2+PR2=2PQ2,
即.
设点P的坐标为(t,﹣t2﹣2t+3)(其中﹣3<t<0),则点Q(t,t+3),
∴PQ=﹣t2﹣2t+3﹣(t+3)=﹣t2﹣3t=﹣(t+)2+.
∵﹣1<0,
∴当时,PQ有最大值.
∴QR的最大值为.
此时,点P的坐标为;
(3)由题意得:将抛物线y=﹣x2﹣2x+3向右平移3个单位后的新抛物线解析式为y=﹣(x﹣2)2+4=﹣x2+4x,点B(1,0)平移后的对应点为D(4,0),
∵新抛物线y=﹣(x﹣2)2+4的对称轴为直线x=2,
∴设E(2,m),F(n,﹣n2+4n),
由(2)知P,
分情况讨论:
①当PF、DE为对角线时,则﹣+n=2+4,
解得:n=,
∴F1(,﹣);
②当DF、EP为对角线时,n+4=﹣+2,
解得:n=﹣,
∴F2(﹣,﹣);
③当EF、DP为对角线时,n+2=﹣+4,
解得:n=,
∴F3(,);
综上所述,点F的坐标为:F1(,﹣),F2(﹣,﹣),F3(,).
同课章节目录
