江苏省洪泽中学高二数学周练试卷及答案(圆锥曲线部分)
文档属性
| 名称 | 江苏省洪泽中学高二数学周练试卷及答案(圆锥曲线部分) |  | |
| 格式 | rar | ||
| 文件大小 | 94.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-11-22 02:07:00 | ||
图片预览


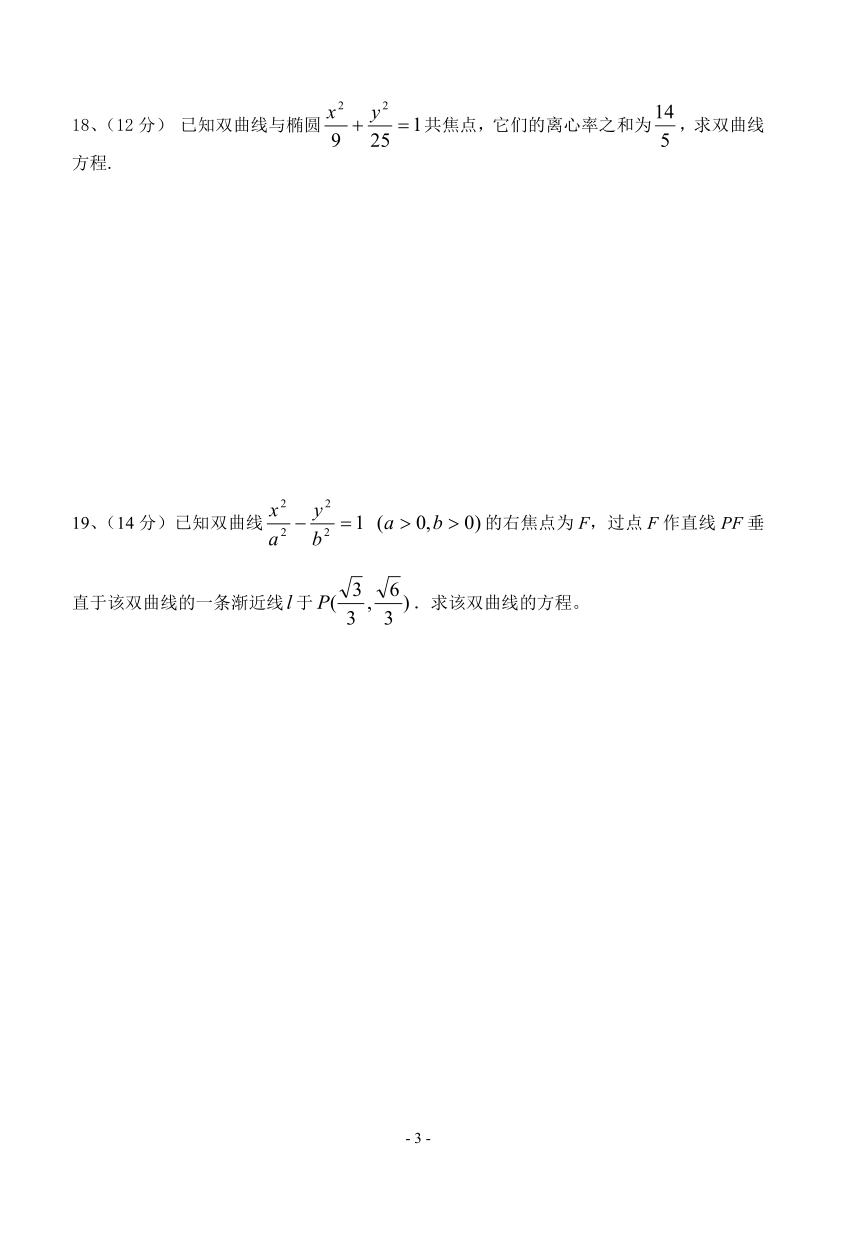
文档简介
江苏省洪泽中学高二数学周练试卷
总分150分
选择题:(每小题5 分,共10小题,满分50分)
1、方程表示的曲线是
椭圆 B、双曲线 C、抛物线 D、不能确定
2、对抛物线,下列描述正确的是
A、开口向上,焦点为 B、开口向上,焦点为
C、开口向右,焦点为 D、开口向右,焦点为
3、椭圆的一个焦点是,那么实数的值为
A、 B、 C、 D、
4、若抛物线y2=2px (p<0)上横坐标为-6的点到焦点的距离是10, 则焦点到准线的距离是
A、4 B、8 C、16 D、32
5. 在同一坐标系中,方程a2x2+b2y2=1与ax+by2=0(a>b>0)的曲线大致是
6、椭圆上有n个不同的点: P1, P2, …, Pn, 椭圆的右焦点为F. 数列{|PnF|}是公差大于的等差数列, 则n的最大值是
A、198 B、199 C、200 D、201
7、已知双曲线的右焦点为F,若过点F且倾斜角为的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是
A、 B、 C、 D、
8、若抛物线的焦点与椭圆的右焦点重合,则的值为
A、 B、 C、 D、
9.若双曲线的渐近线方程为,则双曲线焦点F到渐近线的距离为 ( )
A.2 B. C. D.2
10、已知双曲线的两条渐近线的夹角为,则双曲线的离心率为
A、 B、 C、 D、2
填空题:(每小题5分,共6小题,满分30分)
11、椭圆的焦点为F1、F2,点P为其上的动点,当为钝角时,则P点横坐标的范围为 .
12、过抛物线的焦点的直线交抛物线于A、B两点,O为坐标原点,则
= .
13、设抛物线y2=2px (p>0)上各点到直线3x+4y+12=0的距离的最小值为1,则p= .
14、双曲线上有一点P到左准线的距离为8,则P点到右焦点的距离为 .
15、以为中点的抛物线的弦所在直线方程为: .
16、已知动圆M与 y轴相切,且与定圆C:相内切,则动圆圆心M的轨迹方程为 ▲ .
三、解答题(70′)
17、(12分)已知椭圆C的焦点F1(-,0)和F2(,0),长轴长6,设直线交椭圆C于A、B两点,求线段AB的中点坐标。
18、(12分) 已知双曲线与椭圆共焦点,它们的离心率之和为,求双曲线方程.
19、(14分)已知双曲线的右焦点为F,过点F作直线PF垂直于该双曲线的一条渐近线于.求该双曲线的方程。
20(15分)某隧道横断面由抛物线及矩形的三边组成,尺寸如图,某卡车空车时能通过此隧道,现载一集装箱,箱宽3m,车与箱共高4.5m,此车能否通过此隧道?说明理由。
21.(本题满分17分)已知平面内的一个动点到直线的距离与到定点的距离之比为,设动点的轨迹为,点
⑴求动点的轨迹的方程;
⑵若为轨迹上的动点,求线段中点的轨迹方程;
⑶过原点的直线交轨迹为于,求面积最大值。
江苏省洪泽中学高二数学周练试卷
参考答案
一、选择题(50′)
1
2
3
4
5
6
7
8
9
10
A
B
D
B
C
D
C
D
C
D
二、填空题(30′)
11
12
-3
13
14
2或18
15
16
当x>0时,y=0(x≠0),当x<0时,y2=4ax
三、解答题(80′)
17、解:由已知条件得椭圆的焦点在x轴上,其中c=,a=3,从而b=1,所以其标准方程是:
.联立方程组,消去y得, .
设A(),B(),AB线段的中点为M()那么: ,=
所以=+2=.
也就是说线段AB中点坐标为(-,).
18、解:由于椭圆焦点为F(0,4),离心率为e=,所以双曲线的焦点为F(0,4),离心率为2, 从而c=4,a=2,b=2.
所以求双曲线方程为: .
19、解:设F(c,0),
解方程组得 ……………………………………6
又已知
∴双曲线方程为 ……………………………10
20答案在《课时训练》第52页上
21.⑴设,由题意化简得……5分
⑵设,,由题意得:解得
代入 得
即………………………………………………10分
⑶若斜率不存在时,面积为。
设斜率为,则的方程为,到的距离为
由消去得,所以
的最大值为 17分
总分150分
选择题:(每小题5 分,共10小题,满分50分)
1、方程表示的曲线是
椭圆 B、双曲线 C、抛物线 D、不能确定
2、对抛物线,下列描述正确的是
A、开口向上,焦点为 B、开口向上,焦点为
C、开口向右,焦点为 D、开口向右,焦点为
3、椭圆的一个焦点是,那么实数的值为
A、 B、 C、 D、
4、若抛物线y2=2px (p<0)上横坐标为-6的点到焦点的距离是10, 则焦点到准线的距离是
A、4 B、8 C、16 D、32
5. 在同一坐标系中,方程a2x2+b2y2=1与ax+by2=0(a>b>0)的曲线大致是
6、椭圆上有n个不同的点: P1, P2, …, Pn, 椭圆的右焦点为F. 数列{|PnF|}是公差大于的等差数列, 则n的最大值是
A、198 B、199 C、200 D、201
7、已知双曲线的右焦点为F,若过点F且倾斜角为的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是
A、 B、 C、 D、
8、若抛物线的焦点与椭圆的右焦点重合,则的值为
A、 B、 C、 D、
9.若双曲线的渐近线方程为,则双曲线焦点F到渐近线的距离为 ( )
A.2 B. C. D.2
10、已知双曲线的两条渐近线的夹角为,则双曲线的离心率为
A、 B、 C、 D、2
填空题:(每小题5分,共6小题,满分30分)
11、椭圆的焦点为F1、F2,点P为其上的动点,当为钝角时,则P点横坐标的范围为 .
12、过抛物线的焦点的直线交抛物线于A、B两点,O为坐标原点,则
= .
13、设抛物线y2=2px (p>0)上各点到直线3x+4y+12=0的距离的最小值为1,则p= .
14、双曲线上有一点P到左准线的距离为8,则P点到右焦点的距离为 .
15、以为中点的抛物线的弦所在直线方程为: .
16、已知动圆M与 y轴相切,且与定圆C:相内切,则动圆圆心M的轨迹方程为 ▲ .
三、解答题(70′)
17、(12分)已知椭圆C的焦点F1(-,0)和F2(,0),长轴长6,设直线交椭圆C于A、B两点,求线段AB的中点坐标。
18、(12分) 已知双曲线与椭圆共焦点,它们的离心率之和为,求双曲线方程.
19、(14分)已知双曲线的右焦点为F,过点F作直线PF垂直于该双曲线的一条渐近线于.求该双曲线的方程。
20(15分)某隧道横断面由抛物线及矩形的三边组成,尺寸如图,某卡车空车时能通过此隧道,现载一集装箱,箱宽3m,车与箱共高4.5m,此车能否通过此隧道?说明理由。
21.(本题满分17分)已知平面内的一个动点到直线的距离与到定点的距离之比为,设动点的轨迹为,点
⑴求动点的轨迹的方程;
⑵若为轨迹上的动点,求线段中点的轨迹方程;
⑶过原点的直线交轨迹为于,求面积最大值。
江苏省洪泽中学高二数学周练试卷
参考答案
一、选择题(50′)
1
2
3
4
5
6
7
8
9
10
A
B
D
B
C
D
C
D
C
D
二、填空题(30′)
11
12
-3
13
14
2或18
15
16
当x>0时,y=0(x≠0),当x<0时,y2=4ax
三、解答题(80′)
17、解:由已知条件得椭圆的焦点在x轴上,其中c=,a=3,从而b=1,所以其标准方程是:
.联立方程组,消去y得, .
设A(),B(),AB线段的中点为M()那么: ,=
所以=+2=.
也就是说线段AB中点坐标为(-,).
18、解:由于椭圆焦点为F(0,4),离心率为e=,所以双曲线的焦点为F(0,4),离心率为2, 从而c=4,a=2,b=2.
所以求双曲线方程为: .
19、解:设F(c,0),
解方程组得 ……………………………………6
又已知
∴双曲线方程为 ……………………………10
20答案在《课时训练》第52页上
21.⑴设,由题意化简得……5分
⑵设,,由题意得:解得
代入 得
即………………………………………………10分
⑶若斜率不存在时,面积为。
设斜率为,则的方程为,到的距离为
由消去得,所以
的最大值为 17分
