数学人教A版(2019)选择性必修第三册8.2.1一元线性回归模型(共18张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第三册8.2.1一元线性回归模型(共18张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-05 10:34:47 | ||
图片预览





文档简介
(共18张PPT)
8.2.1 一元线性回归模型
一、线性相关系数 r 的性质
引
01
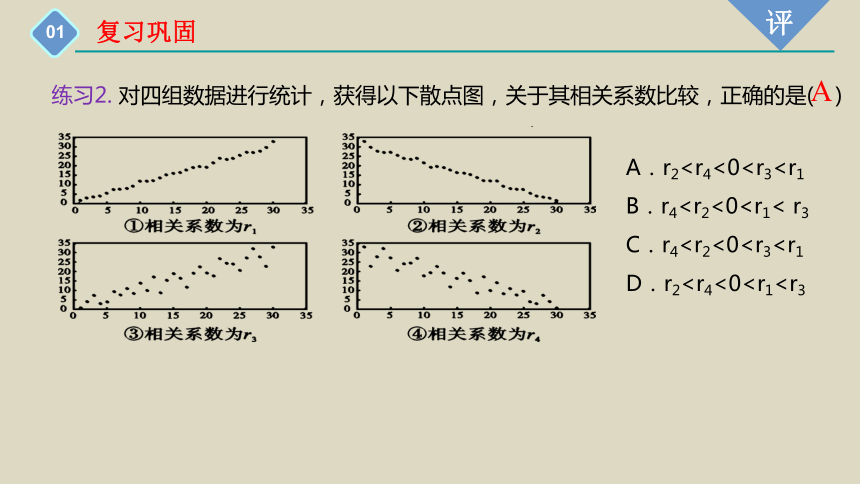
复习巩固
散点集中于一条直线上
(1)当r >0时,称成对样本数据正相关; 当r <0时,称成对样本数据负相关.
样本相关系数 r 可以反映两个随机变量之间的线性相关程度
线性相关程度越强
0
1
线性相关程度越弱
(2)
(3)当|r| = 1时,样本点(散点)集中于某条直线(都在直线上);
(4)当 r= 0时,成对样本数据间没有线性相关关系,但不排除它们之间有其他相关关系。
评
01
复习巩固
A.r2B.r4C.r4D.r2A
引
01
问题情境
散点图 成对样本数据的相关性;
样本线性相关系数 成对样本数据相关的正负性和线性相关程度.
定量
分析
统计分析 预测
服务
能否像建立函数模型刻画两个变量之间的确定性关系那样,通过建立适当的统计模型刻画两个随机变量的相关关系。
进而利用这个模型研究两个变量之间的随机关系,并通过模型进行预测.
评
02
建构新知
引
01
学习目标
1. 理解一元线性回归模型的表达式及模型中参数的意义;
2.通过用数学方法刻画散点与直线接近的程度,体会一元线性回归模型参数的最小二乘估计原理,能推导参数估计公式,发展数学运算能力.
4.通过对残差和残差图的分析,能用残差判断一元线性回归模型的有效性,发展数据分析能力.
核心素养:直观想象,数学运算,数据分析,数学建模.
重点:能根据实例,通过分析变量间的关系建立一元线性回归模型.
难点: 参数估计值公式的推导,利用残差分析回归模型
评
02
研读课本P105-P112,并思考下面的问题
1.根据表8.2-1中的数据,儿子身高和父亲身高这两个变量之间的关系可以用什么样的函数模型刻画?
2.为什么要假设E(e)=0,而不假设其为某个不为0的常数?
3.在一元线性回归模型(1)中,参数b的含义是什么?
4.当x=176时, ,如果一位父亲身高为176cm,他儿子长大后身高一定能长到177cm吗?为什么?
评
02
建构新知
生活经验告诉我们,儿子的身高与父亲的身高相关.一般来说,父亲的身高较高时,儿子的身高通常也较高.为了进一步研究两者之间的关系,有人调查了14名男大学生的身高及其父亲的身高,得到的数据如表1所示.
根据上节课的方法: 样本线性相关系数r =0.886.
父亲身高/cm
180
175
170
165
160
160
165
170
175
180
185
190
·
·
·
·
·
·
·
儿子身高/cm
·
·
·
·
·
·
·
185
可知:儿子的身高与父亲的身高正线性相关,且相关程度很强.
追问1: 是否可以用函数模型来刻画?
评
02
建构新知
追问2: 影响儿子身高的其他因素是什么?
父亲身高/cm
180
175
170
165
160
160
165
170
175
180
185
190
·
·
·
·
·
·
·
儿子身高/cm
·
·
·
·
·
·
·
185
由于儿子身高与父亲身高 线性相关,用 表示父亲身高,Y表示儿子的身高
(e表示各种其它随机因素影响之和,称e为随机误差)
由于随机误差表示大量已知和未知的各种影响之和,它们会相互抵消,为使问题简洁,可以假设随机误差e的均值为0,方差为与父亲身高无关的定值 .
①
称①式为一元线性回归模型
解释变量x (身高)
随机误差e (其它所有变量)
响应变量Y(体重)
评
02
建构新知
①
对于一名男大学生的父亲身高为 ,
而男大学生的实际身高(观测值) 不一定就等于模型得到的均值 ,
评
02
建构新知
(1)除父亲身高外,其他可能影响儿子身高的因素,比如母亲身高、生活环境、饮食习惯和锻炼时间等.
(2)在测量儿子身高时,由于测量工具、测量精度所产生的测量误差.
(3)实际问题中,我们不知道儿子身高和父亲身高的相关关系是什么,可以利用一元线性回归模型来近似这种关系,这种近似关系也是产生随机误差e的原因.
产生随机误差e的原因有:
8.2.2 一元线性回归模型的参数的最小二乘估计
评
02
建构新知
在一元线性回归模型中,表达式 Y=bx+a+e,刻画的是变量 Y 与变量 x 之间的线性关系,但其中参数 a和 b 未知。
评
02
建构新知
1. 最小二乘法
我们将 称为Y 关于x 的经验回归方程,也称经验回归函数或经验回归公式,其图形称为经验回归直线,这种求经验回归方程的方法叫最小二乘法.
“二乘”意为 乘方
评
02
建构新知
依据用最小二乘估计一元线性回归模型参数的公式,求出儿子身高Y关于父亲身高x的经验回归方程:
评
02
建构新知
1) 当x=176时, ,如果一位父亲身高为176cm,他儿子长大后身高一定能长到177cm吗?为什么?
不一定,
因为还有其他影响儿子身高的因素,回归模型中的随机误差清楚地表达了这种影响.
我们可以作出推测: 当父亲的身高为176cm时,儿子身高一般在177cm左右.
2)斜率0.839有什么含义?
0.839可以解释为父亲身高每增加1cm,其儿子的身高平均增加0.839cm.
但由模型可以发现,高个子父亲x=185(cm),则
评
02
建构新知
父亲身高/cm
180
175
170
165
160
160
165
170
175
180
185
190
·
·
·
·
·
·
·
儿子身高/cm
·
·
·
·
·
·
·
185
矮个子父亲x=170(cm),则
把这种后代的的身高向中间值靠近的趋势称为
“回归现象”。
结
05
课堂小结
1.本节课我们尽力怎样的学习过程?
2.学习了哪些新知识、方法?
①
称①式为一元线性回归模型
2) 最小二乘法
8.2.1 一元线性回归模型
一、线性相关系数 r 的性质
引
01
复习巩固
散点集中于一条直线上
(1)当r >0时,称成对样本数据正相关; 当r <0时,称成对样本数据负相关.
样本相关系数 r 可以反映两个随机变量之间的线性相关程度
线性相关程度越强
0
1
线性相关程度越弱
(2)
(3)当|r| = 1时,样本点(散点)集中于某条直线(都在直线上);
(4)当 r= 0时,成对样本数据间没有线性相关关系,但不排除它们之间有其他相关关系。
评
01
复习巩固
A.r2
引
01
问题情境
散点图 成对样本数据的相关性;
样本线性相关系数 成对样本数据相关的正负性和线性相关程度.
定量
分析
统计分析 预测
服务
能否像建立函数模型刻画两个变量之间的确定性关系那样,通过建立适当的统计模型刻画两个随机变量的相关关系。
进而利用这个模型研究两个变量之间的随机关系,并通过模型进行预测.
评
02
建构新知
引
01
学习目标
1. 理解一元线性回归模型的表达式及模型中参数的意义;
2.通过用数学方法刻画散点与直线接近的程度,体会一元线性回归模型参数的最小二乘估计原理,能推导参数估计公式,发展数学运算能力.
4.通过对残差和残差图的分析,能用残差判断一元线性回归模型的有效性,发展数据分析能力.
核心素养:直观想象,数学运算,数据分析,数学建模.
重点:能根据实例,通过分析变量间的关系建立一元线性回归模型.
难点: 参数估计值公式的推导,利用残差分析回归模型
评
02
研读课本P105-P112,并思考下面的问题
1.根据表8.2-1中的数据,儿子身高和父亲身高这两个变量之间的关系可以用什么样的函数模型刻画?
2.为什么要假设E(e)=0,而不假设其为某个不为0的常数?
3.在一元线性回归模型(1)中,参数b的含义是什么?
4.当x=176时, ,如果一位父亲身高为176cm,他儿子长大后身高一定能长到177cm吗?为什么?
评
02
建构新知
生活经验告诉我们,儿子的身高与父亲的身高相关.一般来说,父亲的身高较高时,儿子的身高通常也较高.为了进一步研究两者之间的关系,有人调查了14名男大学生的身高及其父亲的身高,得到的数据如表1所示.
根据上节课的方法: 样本线性相关系数r =0.886.
父亲身高/cm
180
175
170
165
160
160
165
170
175
180
185
190
·
·
·
·
·
·
·
儿子身高/cm
·
·
·
·
·
·
·
185
可知:儿子的身高与父亲的身高正线性相关,且相关程度很强.
追问1: 是否可以用函数模型来刻画?
评
02
建构新知
追问2: 影响儿子身高的其他因素是什么?
父亲身高/cm
180
175
170
165
160
160
165
170
175
180
185
190
·
·
·
·
·
·
·
儿子身高/cm
·
·
·
·
·
·
·
185
由于儿子身高与父亲身高 线性相关,用 表示父亲身高,Y表示儿子的身高
(e表示各种其它随机因素影响之和,称e为随机误差)
由于随机误差表示大量已知和未知的各种影响之和,它们会相互抵消,为使问题简洁,可以假设随机误差e的均值为0,方差为与父亲身高无关的定值 .
①
称①式为一元线性回归模型
解释变量x (身高)
随机误差e (其它所有变量)
响应变量Y(体重)
评
02
建构新知
①
对于一名男大学生的父亲身高为 ,
而男大学生的实际身高(观测值) 不一定就等于模型得到的均值 ,
评
02
建构新知
(1)除父亲身高外,其他可能影响儿子身高的因素,比如母亲身高、生活环境、饮食习惯和锻炼时间等.
(2)在测量儿子身高时,由于测量工具、测量精度所产生的测量误差.
(3)实际问题中,我们不知道儿子身高和父亲身高的相关关系是什么,可以利用一元线性回归模型来近似这种关系,这种近似关系也是产生随机误差e的原因.
产生随机误差e的原因有:
8.2.2 一元线性回归模型的参数的最小二乘估计
评
02
建构新知
在一元线性回归模型中,表达式 Y=bx+a+e,刻画的是变量 Y 与变量 x 之间的线性关系,但其中参数 a和 b 未知。
评
02
建构新知
1. 最小二乘法
我们将 称为Y 关于x 的经验回归方程,也称经验回归函数或经验回归公式,其图形称为经验回归直线,这种求经验回归方程的方法叫最小二乘法.
“二乘”意为 乘方
评
02
建构新知
依据用最小二乘估计一元线性回归模型参数的公式,求出儿子身高Y关于父亲身高x的经验回归方程:
评
02
建构新知
1) 当x=176时, ,如果一位父亲身高为176cm,他儿子长大后身高一定能长到177cm吗?为什么?
不一定,
因为还有其他影响儿子身高的因素,回归模型中的随机误差清楚地表达了这种影响.
我们可以作出推测: 当父亲的身高为176cm时,儿子身高一般在177cm左右.
2)斜率0.839有什么含义?
0.839可以解释为父亲身高每增加1cm,其儿子的身高平均增加0.839cm.
但由模型可以发现,高个子父亲x=185(cm),则
评
02
建构新知
父亲身高/cm
180
175
170
165
160
160
165
170
175
180
185
190
·
·
·
·
·
·
·
儿子身高/cm
·
·
·
·
·
·
·
185
矮个子父亲x=170(cm),则
把这种后代的的身高向中间值靠近的趋势称为
“回归现象”。
结
05
课堂小结
1.本节课我们尽力怎样的学习过程?
2.学习了哪些新知识、方法?
①
称①式为一元线性回归模型
2) 最小二乘法
