人教版七年级数学上册4.1.2点、线、面、体 导学案(知识清单+典型例题+巩固提升)(含解析)
文档属性
| 名称 | 人教版七年级数学上册4.1.2点、线、面、体 导学案(知识清单+典型例题+巩固提升)(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 452.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-05 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版七年级数学上册 4.1.2 点、线、面、体 导学案
【知识清单】
1、立体图形是几何体,简称体;包围着体的是面,面有平面和曲面;面和面相交的地方形成线,线有直线和曲线;线和线相交的地方是点。
2、几何图形都是由点、线、面、体组成,点是构成图形的基本元素。
【典型例题】
考点1:点、线、面、体四者之间的关系
例1.我们如果将一枚硬币竖立在桌面,击打一侧使其快速旋转,就会看到一个“球”,这种现象说明( ).
A.点动成线 B.线动成面 C.面动成体 D.什么都不能说明
【答案】C
【分析】根据面动成体的意义进行说明即可.
【详解】解:硬币是面,旋转得到球体,
属于面动成体,
故选C.
【点睛】本题考查点、线、面、体,理解“点动成线,线动成面,面动成体”是正确解答的前提.
考点2:平面图形旋转后所得的立体图形
例2.下列图形中,以直线为轴旋转一周,可以形成圆柱的是( )
A. B. C. D.
【答案】A
【分析】根据面动成体进行判断即可.
【详解】解:将长方形绕着一条边所在的直线旋转一周,可以得到圆柱体,
故选:A.
【点睛】本题考查点、线、面、体,理解“点动成线,线动成面,面动成体”是正确解答的前提.
考点3:截一个几何体
例3.把一个棱长6分米的正方体木块削成一个最大的圆锥,体积是( )立方分米(π取3.14)
A.28.26 B.169.56 C.100.48 D.56.52
【答案】D
【分析】根据题意可知,圆锥的底面在正方体的一个面上,底面半径为,该圆锥的高为,然后利用圆锥体积公式求解即可.
【详解】根据题意可知,圆锥的底面在正方体的一个面上,底面半径为,该圆锥的高为.
.
故选:D.
【点睛】本题主要考查几何图形,解题的关键在于根据题意构建出符合条件的几何体.
【巩固提升】
1.在朱自清的《春》中描写春雨“像牛毛、像花针、像细丝,密密麻麻地斜织着”的语句,这里把雨看成了线,这说明了( )
A.点动成线 B.线动成面 C.面动成体 D.两点确定一条直线
2.当你用笔在纸上写字时,你的笔尖实现了( )
A.点动成线 B.线动成面 C.面动成体 D.以上都不对
3.一个长方形的长是4厘米,宽是2厘米.以它的宽为轴旋转一周所得到的圆柱体的体积是( )立方厘米.
A. B. C. D.
4.如图1,是直角三角形斜边上的高,将直角三角形按以下方式旋转可以得到图2所示的几何体的是( )
A.绕旋转一周 B.绕旋转一周 C.绕旋转一周 D.绕旋转一周
5.如图是一个长和宽分别为和的长方形,将其按一定方式进行旋转,能得到不同的圆柱( )
A.2种 B.3种 C.4种 D.无数种
6.用一个平面取截一个几何体,得到的截面是三角形,这个几何体可能是( )
A.圆柱 B.圆锥 C.球体 D.以上都有可能
7.如图,圆柱形桶中装一半的水,将桶水平放置,此时桶中水面的形状是( )
A.B. C. D.
8.如图是将正方体切去一个角后的几何体,则该几何体有( )
A.7个面,14条棱 B.6个面,12条棱
C.7个面,12条棱 D.8个面,13条棱
二、填空题
9.天空中的流星划出一条长长的光线,说明 .
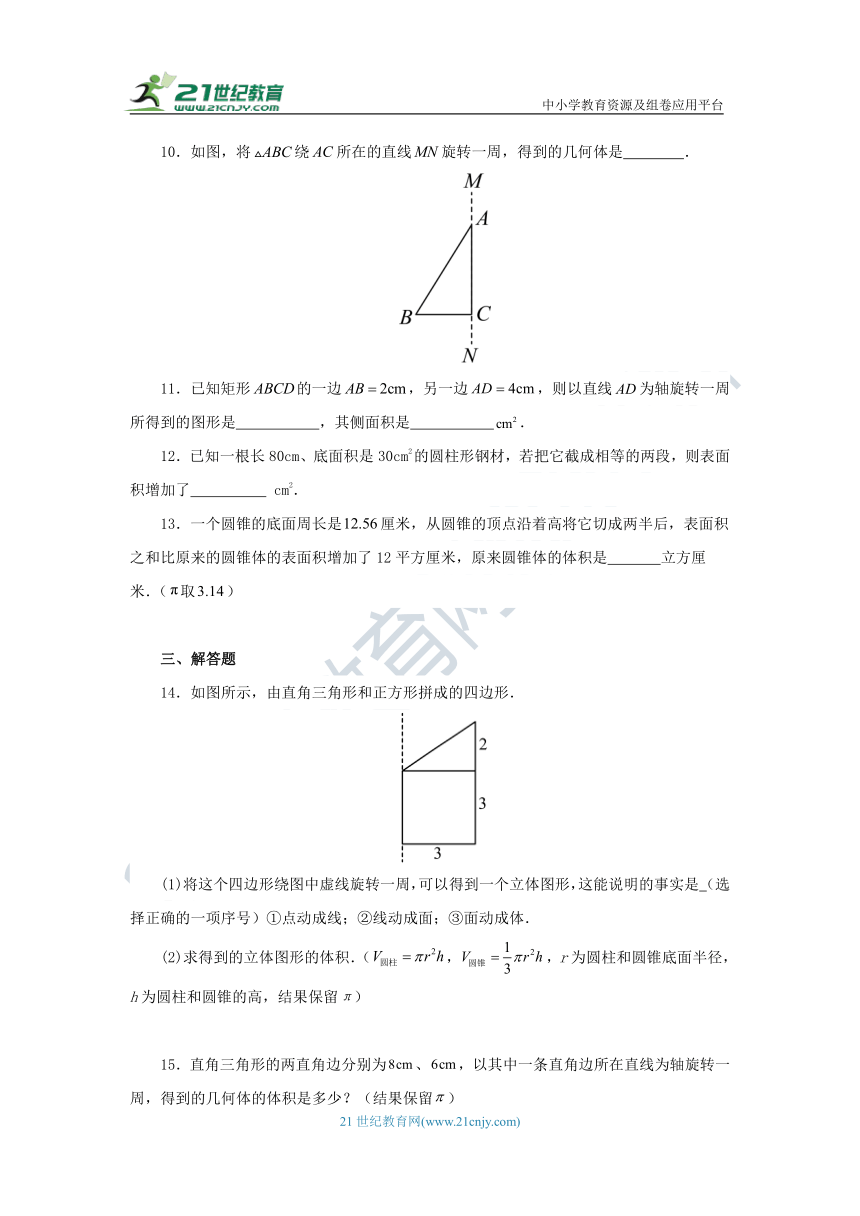
10.如图,将绕所在的直线旋转一周,得到的几何体是 .
11.已知矩形的一边,另一边,则以直线为轴旋转一周所得到的图形是 ,其侧面积是 .
12.已知一根长80cm、底面积是30cm2的圆柱形钢材,若把它截成相等的两段,则表面积增加了 cm2.
13.一个圆锥的底面周长是厘米,从圆锥的顶点沿着高将它切成两半后,表面积之和比原来的圆锥体的表面积增加了12平方厘米,原来圆锥体的体积是 立方厘米.(取)
三、解答题
14.如图所示,由直角三角形和正方形拼成的四边形.
(1)将这个四边形绕图中虚线旋转一周,可以得到一个立体图形,这能说明的事实是 (选择正确的一项序号)①点动成线;②线动成面;③面动成体.
(2)求得到的立体图形的体积.(,,r为圆柱和圆锥底面半径,h为圆柱和圆锥的高,结果保留π)
15.直角三角形的两直角边分别为、,以其中一条直角边所在直线为轴旋转一周,得到的几何体的体积是多少?(结果保留)
16.已知长方形的长为,宽为,将其绕它的一边所在的直线旋转一周,得到一个立体图形.
(1)得到的立体图形的名称是______;
(2)求这个几何体的表面积.(结果保留).
17.“乾隆通宝”是最具代表性的中国古代货币之一,为典型的圆形方孔形态,其钱径(货币直径)一般约厘米,厚厘米,重约克,中间方孔的边长为钱径的四分之一.图是一枚钱径为厘米的“乾隆通宝”钱币.(此题计算过程中圆周率取值均为3)
(1)请你在平面图中用作图的方式标出“乾隆通宝”钱币的中心点O.
(2)请你计算出平面图中阴影部分的面积是多少平方厘米?
(3)若将钱币绕过中心点O的竖直直线旋转一周(钱币厚度忽略不计),试求方孔旋转后得到的新图形的体积.
18.如图是一个圆柱,任意切一刀,切口会是什么形状 请画出两种可能的图形.
19.如图是一块长为的长方体木块,点把棱分成的两段,过点按平行于平面的方向把长方体切成两块后,表面积增加了,问:这两块长方体的体积分别是多少立方厘米?
参考答案
1.A
【分析】根据点动成线,线动成面,面动成体,即可解答.
【详解】解:在朱自清的《春》中描写春雨“像牛毛、像花针、像细丝,密密麻麻地斜织着”的语句,这里把雨看成了线,这说明了:点动成线,
故选:A.
【点睛】本题考查了点、线、面、体的关系,掌握点动成线,线动成面,面动成体,是解题的关键.
2.A
【分析】笔尖点在纸上是一个点,写字滑动笔尖就是一条直线,即点动成线.
【详解】解:当你用笔在纸上写字时,你的笔尖实现了点动成线,
故选:A.
【点睛】本题考查了点动成线,理解点动成线是解题关键.
3.A
【分析】根据题意得出圆柱体底面半径和高,利用体积公式即可求解.
【详解】解:由题意知,圆柱体底面半径为4厘米,高为2厘米,
故圆柱体的体积为:.
故选A.
【点睛】本题考查圆柱体积的计算,解题的关键是找出圆柱的底面半径和高.
4.D
【分析】根据直角三角形的性质,只有绕斜边旋转一周,才可以得出组合体的圆锥,进而解答即可.
【详解】解:将直角三角形绕斜边所在直线旋转一周得到的几何体是图2的形状,
故选:B.
【点睛】本题考查了点、线、面、体,培养学生的空间想象能力及几何体的三视图.
5.D
【分析】以平行于长或宽所在直线为旋转轴可以得到无数种.
【详解】解:以平行于长或宽所在直线为旋转轴可以得到无数种不同的圆柱体.
故选:D.
【点睛】此题考查了点、线、面、体的关系,关键是掌握面动成体.
6.B
【分析】圆锥沿顶点可以截出三角形,结合选项选出正确答案即可.
【详解】解:A、用平面截圆柱,截面不是三角形,故本选项不符合题意;
B、用平面截圆锥,截面可能是三角形,故本选项符合题意;
C、用平面截球,截面是圆形,故本选项不符合题意;
D、由于用平面截圆锥截面可能是三角形,可知本选项不符合题意.
故选:B.
【点睛】本题考查了常见几何体形状以及截面形状,截面的形状既与被截的几何体有关,还与截面的角度和方向有关.截面是三角形,满足这一条件的几何体有圆锥、棱柱、正方体等.
7.C
【分析】由题意可得水面的形状是平面,用平行于底面的这个平面截这个圆柱体,所得到的截面的形状即为所求.
【详解】解:桶内水面的形状,就是用平行于底面的平面截这个圆柱体所得到的截面的形状,
而圆柱体用平行于底面的平面去截可得到长方形的截面.
故选:C.
【点睛】本题主要考查了截几何体,较好的空间想象能力是解答本题的关键.
8.A
【分析】根据正方体的面数与棱数,切去一个角后,面数与棱数的变化,即可得到面数与棱数.
【详解】解:正方体有6个面12条棱,将正方体切去一个角后的几何体,面增加一个,棱增加2条,此时的几何体共有7个面,14条棱.
故选:A.
【点睛】本题考查了求几何体截去一个角后面数与棱数,要求学生具备一定的空间想象力.
9.点动成线
【分析】由点动成线的含义进行分析解答即可.
【详解】解:夜晚天空中的流星划出一条长长的光线,由此说明了点动成线的数学事实,
故答案为:点动成线.
【点睛】本题考查了点动成线,熟练掌握点动成线的含义是解答本题的关键.
10.圆锥
【分析】根据面动成体进行判断即可.
【详解】解:将绕所在的直线旋转一周,得到的几何体是圆锥.
故答案为:圆锥.
【点睛】本题主要考查了面动成体,解题的关键是数形结合,熟练掌握点、线、面之间的关系.
11. 圆柱
【分析】一个矩形以一边为轴旋转一周所得到的图形是圆柱,再根据圆柱侧面积=底面周长×高即可求解.
【详解】解:一个矩形以一边为轴旋转一周所得到的图形是圆柱,
圆柱的侧面积为.
故答案为:圆柱,.
【点睛】本题主要考查了圆柱的形成及侧面积的计算方法.
12.60
【分析】将圆柱形钢材截成相等的两段后,表面积增加了两个底面积.据此即可求解.
【详解】解:由题意得:圆柱形钢材截成相等的两段后,表面积增加了两个底面积
故表面积增加了
故答案为:60
【点睛】本题考查了立方体的相关知识.正确理解题意即可.
13.
【分析】通过圆锥的底面周长求出圆锥的直径和半径,再运用三角形的面积公式求出圆锥的高,最后运用圆锥的体积公式求出圆锥的体积.
【详解】解:圆锥体的底面半径为(厘米),直径为(厘米),
圆锥体的高为(厘米),
∴原来圆锥体的体积为(立方厘米),
故答案为:.
【点睛】本题考查了三角形面积公式的运用,圆锥体积公式的运用,圆周长公式的运用,考查学生知识综合运用的能力,熟记公式和正确求解是解答的关键.
14.(1)③
(2)
【分析】(1)由四边形绕图中虚线旋转一周,可以得到一个立体图形可知是面动成体;
(2)分别求出圆柱体和圆锥体的体积,作差即可
【详解】(1)∵四边形是平面图形,绕图中虚线旋转一周,可以得到一个立体图形
∴是面动成体
故选③
(2)∵
∴
【点睛】本题考查面动成体,圆柱和圆锥的体积公式,记忆理解公式是解题的关键
15.或.
【分析】分两种情况讨论:①以的直角边为轴旋转;②以的直角边为轴旋转,得到的几何体为圆锥,再利用圆锥的体积公式即可得到答案.
【详解】解:①以的直角边为轴旋转,得到的是一个底面半径为,高为的圆锥,
体积是:,
②以的直角边为轴旋转,得到的是一个底面半径为,高为的圆锥,
体积是:,
答:绕它的一条直角边旋转一周,得到的几何体的体积是或.
【点睛】本题考查了点、线、面、体,圆锥的体积公式,解题关键是理解点、线、面、体,熟记圆锥体积公式.
16.(1)圆柱
(2)圆柱的表面积为或
【分析】(1)根据面动成体解答即可;
(2)分长方形的长为轴旋转和以长方形的宽为轴旋转两种情况根据圆柱的表面积公式计算即可求解.
【详解】(1)由题意可知,得到的立体图形的名称是圆柱.
故答案为:圆柱.
(2)①以长方形的长为轴旋转,则圆柱的底面半径为,高为,所以圆柱的表面积为().
②以长方形的宽为轴旋转,则圆柱的底面半径为,高为,所以圆柱的表面积为().
综上可得圆柱的表面积为或.
【点睛】本题考查的是点、线、面、体,根据图形确定出圆柱的底面半径和高的长是解题的关键.
17.(1)见解析
(2)
(3)
【分析】(1)连接中间正方形的对角线,交点即为点O;
(2)用圆形的面积减去中间正方形的面积即可;
(3)首先判断出旋转一周后,方孔得到圆柱,再利用体积公式计算即可.
【详解】(1)解:如图,即为所求;
(2)由题意可得:
阴影部分的面积是:;
(3)旋转一周后,方孔得到圆柱,
其中圆柱体的底面直径为,高为,
则新图形的体积为:.
【点睛】本题考查了几何图形的面积和几何体的体积,解题的关键是找到阴影部分面积的计算方法,同时要准确确定旋转后得到的几何体.
18.见解析
【分析】根据几何体的形状得出即可.
【详解】解:沿平行于圆面切得到一个圆形;
沿不平行线圆面切可得到椭圆或梯形;
沿垂直于圆面切可得到一个长方形.
.
【点睛】此题主要考查了截一个几何体,根据已知几何体得出不同的截面是解题关键,截面的形状既与被截的几何体有关,还与截面的角度和方向有关.
19.这两块长方体的体积分别是5600立方厘米、8400立方厘米
【分析】长为的长方体木块,点把棱分成的两段,则可得:(厘米),则(厘米),根据切割特点,表面积是增加了2个正方体的面的面积,据此求出正方体一个面的面积是(平方厘米),据此再利用长方体的体积侧面积×长计算即可解答.
【详解】解:点把棱分成的两段,则可得:(厘米),
则(厘米),
(平方厘米),
(立方厘米),
(立方厘米),
答:这两块长方体的体积分别是5600立方厘米、8400立方厘米.
【点睛】本题考查了截一个几何体、求几何体的表面积.解答此题的关键是明确两部分的长以及横截面的面积.
21世纪教育网(www.21cnjy.com)
人教版七年级数学上册 4.1.2 点、线、面、体 导学案
【知识清单】
1、立体图形是几何体,简称体;包围着体的是面,面有平面和曲面;面和面相交的地方形成线,线有直线和曲线;线和线相交的地方是点。
2、几何图形都是由点、线、面、体组成,点是构成图形的基本元素。
【典型例题】
考点1:点、线、面、体四者之间的关系
例1.我们如果将一枚硬币竖立在桌面,击打一侧使其快速旋转,就会看到一个“球”,这种现象说明( ).
A.点动成线 B.线动成面 C.面动成体 D.什么都不能说明
【答案】C
【分析】根据面动成体的意义进行说明即可.
【详解】解:硬币是面,旋转得到球体,
属于面动成体,
故选C.
【点睛】本题考查点、线、面、体,理解“点动成线,线动成面,面动成体”是正确解答的前提.
考点2:平面图形旋转后所得的立体图形
例2.下列图形中,以直线为轴旋转一周,可以形成圆柱的是( )
A. B. C. D.
【答案】A
【分析】根据面动成体进行判断即可.
【详解】解:将长方形绕着一条边所在的直线旋转一周,可以得到圆柱体,
故选:A.
【点睛】本题考查点、线、面、体,理解“点动成线,线动成面,面动成体”是正确解答的前提.
考点3:截一个几何体
例3.把一个棱长6分米的正方体木块削成一个最大的圆锥,体积是( )立方分米(π取3.14)
A.28.26 B.169.56 C.100.48 D.56.52
【答案】D
【分析】根据题意可知,圆锥的底面在正方体的一个面上,底面半径为,该圆锥的高为,然后利用圆锥体积公式求解即可.
【详解】根据题意可知,圆锥的底面在正方体的一个面上,底面半径为,该圆锥的高为.
.
故选:D.
【点睛】本题主要考查几何图形,解题的关键在于根据题意构建出符合条件的几何体.
【巩固提升】
1.在朱自清的《春》中描写春雨“像牛毛、像花针、像细丝,密密麻麻地斜织着”的语句,这里把雨看成了线,这说明了( )
A.点动成线 B.线动成面 C.面动成体 D.两点确定一条直线
2.当你用笔在纸上写字时,你的笔尖实现了( )
A.点动成线 B.线动成面 C.面动成体 D.以上都不对
3.一个长方形的长是4厘米,宽是2厘米.以它的宽为轴旋转一周所得到的圆柱体的体积是( )立方厘米.
A. B. C. D.
4.如图1,是直角三角形斜边上的高,将直角三角形按以下方式旋转可以得到图2所示的几何体的是( )
A.绕旋转一周 B.绕旋转一周 C.绕旋转一周 D.绕旋转一周
5.如图是一个长和宽分别为和的长方形,将其按一定方式进行旋转,能得到不同的圆柱( )
A.2种 B.3种 C.4种 D.无数种
6.用一个平面取截一个几何体,得到的截面是三角形,这个几何体可能是( )
A.圆柱 B.圆锥 C.球体 D.以上都有可能
7.如图,圆柱形桶中装一半的水,将桶水平放置,此时桶中水面的形状是( )
A.B. C. D.
8.如图是将正方体切去一个角后的几何体,则该几何体有( )
A.7个面,14条棱 B.6个面,12条棱
C.7个面,12条棱 D.8个面,13条棱
二、填空题
9.天空中的流星划出一条长长的光线,说明 .
10.如图,将绕所在的直线旋转一周,得到的几何体是 .
11.已知矩形的一边,另一边,则以直线为轴旋转一周所得到的图形是 ,其侧面积是 .
12.已知一根长80cm、底面积是30cm2的圆柱形钢材,若把它截成相等的两段,则表面积增加了 cm2.
13.一个圆锥的底面周长是厘米,从圆锥的顶点沿着高将它切成两半后,表面积之和比原来的圆锥体的表面积增加了12平方厘米,原来圆锥体的体积是 立方厘米.(取)
三、解答题
14.如图所示,由直角三角形和正方形拼成的四边形.
(1)将这个四边形绕图中虚线旋转一周,可以得到一个立体图形,这能说明的事实是 (选择正确的一项序号)①点动成线;②线动成面;③面动成体.
(2)求得到的立体图形的体积.(,,r为圆柱和圆锥底面半径,h为圆柱和圆锥的高,结果保留π)
15.直角三角形的两直角边分别为、,以其中一条直角边所在直线为轴旋转一周,得到的几何体的体积是多少?(结果保留)
16.已知长方形的长为,宽为,将其绕它的一边所在的直线旋转一周,得到一个立体图形.
(1)得到的立体图形的名称是______;
(2)求这个几何体的表面积.(结果保留).
17.“乾隆通宝”是最具代表性的中国古代货币之一,为典型的圆形方孔形态,其钱径(货币直径)一般约厘米,厚厘米,重约克,中间方孔的边长为钱径的四分之一.图是一枚钱径为厘米的“乾隆通宝”钱币.(此题计算过程中圆周率取值均为3)
(1)请你在平面图中用作图的方式标出“乾隆通宝”钱币的中心点O.
(2)请你计算出平面图中阴影部分的面积是多少平方厘米?
(3)若将钱币绕过中心点O的竖直直线旋转一周(钱币厚度忽略不计),试求方孔旋转后得到的新图形的体积.
18.如图是一个圆柱,任意切一刀,切口会是什么形状 请画出两种可能的图形.
19.如图是一块长为的长方体木块,点把棱分成的两段,过点按平行于平面的方向把长方体切成两块后,表面积增加了,问:这两块长方体的体积分别是多少立方厘米?
参考答案
1.A
【分析】根据点动成线,线动成面,面动成体,即可解答.
【详解】解:在朱自清的《春》中描写春雨“像牛毛、像花针、像细丝,密密麻麻地斜织着”的语句,这里把雨看成了线,这说明了:点动成线,
故选:A.
【点睛】本题考查了点、线、面、体的关系,掌握点动成线,线动成面,面动成体,是解题的关键.
2.A
【分析】笔尖点在纸上是一个点,写字滑动笔尖就是一条直线,即点动成线.
【详解】解:当你用笔在纸上写字时,你的笔尖实现了点动成线,
故选:A.
【点睛】本题考查了点动成线,理解点动成线是解题关键.
3.A
【分析】根据题意得出圆柱体底面半径和高,利用体积公式即可求解.
【详解】解:由题意知,圆柱体底面半径为4厘米,高为2厘米,
故圆柱体的体积为:.
故选A.
【点睛】本题考查圆柱体积的计算,解题的关键是找出圆柱的底面半径和高.
4.D
【分析】根据直角三角形的性质,只有绕斜边旋转一周,才可以得出组合体的圆锥,进而解答即可.
【详解】解:将直角三角形绕斜边所在直线旋转一周得到的几何体是图2的形状,
故选:B.
【点睛】本题考查了点、线、面、体,培养学生的空间想象能力及几何体的三视图.
5.D
【分析】以平行于长或宽所在直线为旋转轴可以得到无数种.
【详解】解:以平行于长或宽所在直线为旋转轴可以得到无数种不同的圆柱体.
故选:D.
【点睛】此题考查了点、线、面、体的关系,关键是掌握面动成体.
6.B
【分析】圆锥沿顶点可以截出三角形,结合选项选出正确答案即可.
【详解】解:A、用平面截圆柱,截面不是三角形,故本选项不符合题意;
B、用平面截圆锥,截面可能是三角形,故本选项符合题意;
C、用平面截球,截面是圆形,故本选项不符合题意;
D、由于用平面截圆锥截面可能是三角形,可知本选项不符合题意.
故选:B.
【点睛】本题考查了常见几何体形状以及截面形状,截面的形状既与被截的几何体有关,还与截面的角度和方向有关.截面是三角形,满足这一条件的几何体有圆锥、棱柱、正方体等.
7.C
【分析】由题意可得水面的形状是平面,用平行于底面的这个平面截这个圆柱体,所得到的截面的形状即为所求.
【详解】解:桶内水面的形状,就是用平行于底面的平面截这个圆柱体所得到的截面的形状,
而圆柱体用平行于底面的平面去截可得到长方形的截面.
故选:C.
【点睛】本题主要考查了截几何体,较好的空间想象能力是解答本题的关键.
8.A
【分析】根据正方体的面数与棱数,切去一个角后,面数与棱数的变化,即可得到面数与棱数.
【详解】解:正方体有6个面12条棱,将正方体切去一个角后的几何体,面增加一个,棱增加2条,此时的几何体共有7个面,14条棱.
故选:A.
【点睛】本题考查了求几何体截去一个角后面数与棱数,要求学生具备一定的空间想象力.
9.点动成线
【分析】由点动成线的含义进行分析解答即可.
【详解】解:夜晚天空中的流星划出一条长长的光线,由此说明了点动成线的数学事实,
故答案为:点动成线.
【点睛】本题考查了点动成线,熟练掌握点动成线的含义是解答本题的关键.
10.圆锥
【分析】根据面动成体进行判断即可.
【详解】解:将绕所在的直线旋转一周,得到的几何体是圆锥.
故答案为:圆锥.
【点睛】本题主要考查了面动成体,解题的关键是数形结合,熟练掌握点、线、面之间的关系.
11. 圆柱
【分析】一个矩形以一边为轴旋转一周所得到的图形是圆柱,再根据圆柱侧面积=底面周长×高即可求解.
【详解】解:一个矩形以一边为轴旋转一周所得到的图形是圆柱,
圆柱的侧面积为.
故答案为:圆柱,.
【点睛】本题主要考查了圆柱的形成及侧面积的计算方法.
12.60
【分析】将圆柱形钢材截成相等的两段后,表面积增加了两个底面积.据此即可求解.
【详解】解:由题意得:圆柱形钢材截成相等的两段后,表面积增加了两个底面积
故表面积增加了
故答案为:60
【点睛】本题考查了立方体的相关知识.正确理解题意即可.
13.
【分析】通过圆锥的底面周长求出圆锥的直径和半径,再运用三角形的面积公式求出圆锥的高,最后运用圆锥的体积公式求出圆锥的体积.
【详解】解:圆锥体的底面半径为(厘米),直径为(厘米),
圆锥体的高为(厘米),
∴原来圆锥体的体积为(立方厘米),
故答案为:.
【点睛】本题考查了三角形面积公式的运用,圆锥体积公式的运用,圆周长公式的运用,考查学生知识综合运用的能力,熟记公式和正确求解是解答的关键.
14.(1)③
(2)
【分析】(1)由四边形绕图中虚线旋转一周,可以得到一个立体图形可知是面动成体;
(2)分别求出圆柱体和圆锥体的体积,作差即可
【详解】(1)∵四边形是平面图形,绕图中虚线旋转一周,可以得到一个立体图形
∴是面动成体
故选③
(2)∵
∴
【点睛】本题考查面动成体,圆柱和圆锥的体积公式,记忆理解公式是解题的关键
15.或.
【分析】分两种情况讨论:①以的直角边为轴旋转;②以的直角边为轴旋转,得到的几何体为圆锥,再利用圆锥的体积公式即可得到答案.
【详解】解:①以的直角边为轴旋转,得到的是一个底面半径为,高为的圆锥,
体积是:,
②以的直角边为轴旋转,得到的是一个底面半径为,高为的圆锥,
体积是:,
答:绕它的一条直角边旋转一周,得到的几何体的体积是或.
【点睛】本题考查了点、线、面、体,圆锥的体积公式,解题关键是理解点、线、面、体,熟记圆锥体积公式.
16.(1)圆柱
(2)圆柱的表面积为或
【分析】(1)根据面动成体解答即可;
(2)分长方形的长为轴旋转和以长方形的宽为轴旋转两种情况根据圆柱的表面积公式计算即可求解.
【详解】(1)由题意可知,得到的立体图形的名称是圆柱.
故答案为:圆柱.
(2)①以长方形的长为轴旋转,则圆柱的底面半径为,高为,所以圆柱的表面积为().
②以长方形的宽为轴旋转,则圆柱的底面半径为,高为,所以圆柱的表面积为().
综上可得圆柱的表面积为或.
【点睛】本题考查的是点、线、面、体,根据图形确定出圆柱的底面半径和高的长是解题的关键.
17.(1)见解析
(2)
(3)
【分析】(1)连接中间正方形的对角线,交点即为点O;
(2)用圆形的面积减去中间正方形的面积即可;
(3)首先判断出旋转一周后,方孔得到圆柱,再利用体积公式计算即可.
【详解】(1)解:如图,即为所求;
(2)由题意可得:
阴影部分的面积是:;
(3)旋转一周后,方孔得到圆柱,
其中圆柱体的底面直径为,高为,
则新图形的体积为:.
【点睛】本题考查了几何图形的面积和几何体的体积,解题的关键是找到阴影部分面积的计算方法,同时要准确确定旋转后得到的几何体.
18.见解析
【分析】根据几何体的形状得出即可.
【详解】解:沿平行于圆面切得到一个圆形;
沿不平行线圆面切可得到椭圆或梯形;
沿垂直于圆面切可得到一个长方形.
.
【点睛】此题主要考查了截一个几何体,根据已知几何体得出不同的截面是解题关键,截面的形状既与被截的几何体有关,还与截面的角度和方向有关.
19.这两块长方体的体积分别是5600立方厘米、8400立方厘米
【分析】长为的长方体木块,点把棱分成的两段,则可得:(厘米),则(厘米),根据切割特点,表面积是增加了2个正方体的面的面积,据此求出正方体一个面的面积是(平方厘米),据此再利用长方体的体积侧面积×长计算即可解答.
【详解】解:点把棱分成的两段,则可得:(厘米),
则(厘米),
(平方厘米),
(立方厘米),
(立方厘米),
答:这两块长方体的体积分别是5600立方厘米、8400立方厘米.
【点睛】本题考查了截一个几何体、求几何体的表面积.解答此题的关键是明确两部分的长以及横截面的面积.
21世纪教育网(www.21cnjy.com)
