人教版七年级数学上册4.3.1角 导学案(知识清单+典型例题+巩固提升)(含解析)
文档属性
| 名称 | 人教版七年级数学上册4.3.1角 导学案(知识清单+典型例题+巩固提升)(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 484.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-05 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版七年级数学上册 4.3.1 角 导学案
【知识清单】
角:由两条具有公共端点引出射线组成的图形(也可看做是由一射线绕端点旋转而成)。
角的表示:三个大写字母;一个大写字母(不混淆情况下方可使用);一个数字;一个希腊字母。
角的要素:顶点和边,角的大小与边的长短无关。
【典型例题】
考点1:角的概念理解
例1.下列说法中正确的是( )
A.两条射线组成的图形叫做角 B.两点之间直线最短
C.两点确定一条直线 D.若,则点B是的中点
【答案】C
【分析】根据两点确定一条直线,角的定义,线段中点的定义对各选项分析判断后利用排除法求解.
【详解】A、应为有公共端点的两条射线组成的图形叫做角,故本选项错误;
B、应为两点之间线段最短,故本选项错误;
C、两点确定一条直线正确,故本选项正确;
D、若,则点为的中点错误,因为、、三点不一定共线,故本选项错误.
故选:C.
【点睛】本题考查了线段的性质,直线的性质,以及角的定义,是基础题,熟记概念与各性质是解题的关键.
考点2:角的表示方法
例2.下列四个图中,能用三种方法表示同一个角的是( )
A. B.
C. D.
【答案】D
【分析】根据角的表示方法和图形选出即可.
【详解】解:A、图中的不能用表示,故本选项错误;
B、图中的和不是表示同一个角,故本选项错误;
C、图中的和不是表示同一个角,故本选项错误;
D、图中、、表示同一个角,故本选项正确;
故选:D.
【点睛】本题考查了角的表示方法的应用,主要考查学生的理解能力和观察图形的能力.
.
故选:.
【点睛】本题主要考查了方向角,用方向角描述方向时,通常以正北或正南方向为角的始边,以对象所处的射线为终边,故描述方向角时,一般先叙述北或南,再叙述偏东或偏西.
考点3:角的分类
例3.下列说法正确的是( )
A.两点之间,直线最短 B.圆是立体图形
C.小于的角是锐角 D.射线与射线是同一条射线
【答案】C
【分析】根据线段、射线与两点之间的距离等性质依次判断即可.
【详解】解:A、两点之间线段最短,原说法错误,选项错误;
B、圆不是立体图形,原说法错误,选项错误;
C、小于的角是锐角,说法正确,选项正确;
D、射线与射线不是同一条射线,方向相反,原说法错误,选项错误,
故选:C.
【点睛】题目主要考查线段、射线、两点间的距离的性质,熟练掌握各个性质是解题关键.
考点4:画特殊角
例4.下列各度数的角,能借助一副三角尺画出的是( )
A.55° B.65° C.75° D.85°
【答案】C
【分析】一副三角板,度数有:、、、,根据度数组合,可以得到答案.
【详解】解:利用一副三角板可以画出的角,是和角的组合
故选:C.
【点睛】本题考查特殊角的画法,审题清晰是解题关键.
考点5:钟面角
例5.7点分,时钟的时针与分针的夹角为( )
A. B. C. D.
【答案】D
【分析】根据时钟上一大格是,进行计算即可解答.
【详解】解:由题意得:,
故选:D.
【点睛】本题考查了钟面角,熟练掌握时钟上一大格是是解题的关键.
考点6:方向角的表示
例6.观察点不变,观察角度变小,观察的范围( )
A.变小 B.变大 C.不变 D.不确定
【答案】A
【分析】观察点变近,观察的角度不变观察的范围就会变小.观察点不变角度越小,观察的范围就越小.
【详解】解:观察点不变,观察角度变小,观察的范围变小;
故选:A.
【点睛】本题主要考查了观察点,观察角度,观察范围三者之间的关系.
考点7:与方向角有关的计算题
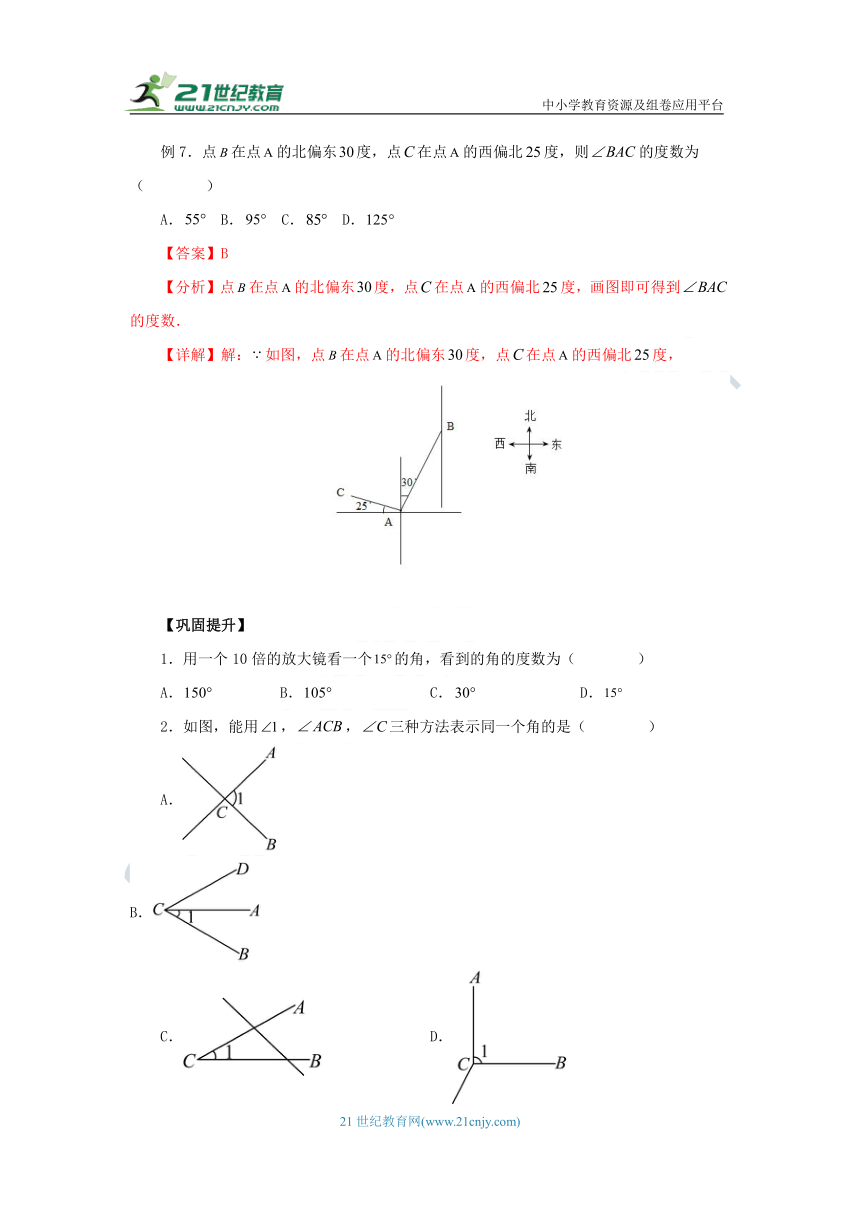
例7.点在点的北偏东度,点在点的西偏北度,则的度数为( )
A. B. C. D.
【答案】B
【分析】点在点的北偏东度,点在点的西偏北度,画图即可得到的度数.
【详解】解:如图,点在点的北偏东度,点在点的西偏北度,
【巩固提升】
1.用一个10倍的放大镜看一个的角,看到的角的度数为( )
A. B. C. D.
2.如图,能用,,三种方法表示同一个角的是( )
A. B.
C. D.
3.下列标注的四个角中,最小的角是( )
A. B. C. D.
4.用一副三角板不能画出的角是( ).
A.75° B.105° C.110° D.135°
5.上午时,钟表的分针与时针夹角的度数是( )
A.105度 B.85度 C.95度 D.115度
6.如图,关于射线所指方向描述正确的是( )
A.东偏北 B.北偏西 C.西偏北 D.南偏西
7.如图,学校A在小明家B北偏东的方向上,点C表示超市所在的位置,,则超市C在小明家B的( )
A.北偏西的方向上 B.北偏西的方向上
C.南偏西的方向上 D.南偏东的方向上
二、填空题
8.如图,则图中共有 个角.
9.角可以分为 、 、 三类.
10.当时间为时,时针和分针所夹角度为 .
11.如图,把一个直径8米的圆平均分成四个扇形,再把每个扇形的弧三等分.点A在点O的 偏 °方向 米处.
12.如图,轮船从出发向北偏东方向航行一段时间到达,又从出发向南偏西方向航行一段时间到达,则 .
三、解答题
13.如图:
(1)以点B为顶点的角有几个?分别表示出来.
(2)请分别指出以射线为边的角.
(3)以D为顶点,为一边的角有几个?分别写出来.
14.写出图中符合下列条件的角.
(1)能用一个大写字母表示的角;
(2)以点为顶点的角;
(3)图中所有小于平角的角(可用简便方法表示).
15.画图,说理题
如图,已知四个点A、B、C、D;
(1)画射线;
(2)画线段;
(3)画;
(4)画出一点P,使P到点A、B、C、D的距离之和最小,并说明理由.
16.按要求解答下面各题.
(1)书店在区政府的( )面( )米处.
(2)图书馆在区政府的( )偏( )( )方向( )米处.
(3)学校在区政府北偏西方向600米处,请列式计算并在图上标出.
17.如图,射线表示的方向是北偏东,射线表示的方向是北偏西,射线在射线和射线之间,且.求的度数.
参考答案
1.D
【分析】把角按一定比例放大或缩小,角的度数不变.
【详解】解:放大镜看一个的角,角的两边的张开程度没变,即角的度数不变,
故选:D.
【点睛】本题考查角的概念,关键是掌握图形的放大或缩小的性质.
2.C
【分析】角的表示方法有三种:(1)用三个字母及符号“”来表示.中间的字母表示顶点,其它两个字母分别表示角的两边上的点.(2)用一个数字表示一个角.(3)用一个字母表示一个角.具体用哪种方法,要根据角的情况进行具体分析,总之表示要明确,不能使人产生误解.
【详解】解:在选项A、B、D中,如果用表示,容易使人产生歧义,
无法让人明确到底表示哪个角;
只有选项C能用,,三种方法表示同一个角,不会使人产生歧义.
故选:C.
【点睛】此题主要考查学生对角的概念和角的表示方法的理解和掌握.通过练习,使学生学会角的表示方法,为今后的学习奠定基础.
3.B
【分析】根据角的分类即可得.
【详解】解:A是钝角,大于小于;B是锐角,小于;C是直角,等于;D是平角,等于,
∴最小的角是锐角,
故选:B.
【点睛】本题考查了角的分类和比较大小,解题的关键是掌握角的分类.
4.C
【分析】105°=60°+45°,105°角可以用一幅三角板中的60°角和45°角画;75°=45°+30°,75°角可以用一幅三角板中的45°角和30°角画;135°=90°+45°,135°角可以用一幅三角板中的直角和90°角或45°角画;110°角用一副三角板不能画出.
【详解】解:105°角可以用一幅三角板中的60°角和45°角画;
75°角可以用一幅三角板中的45°角和30°角画;
110°角用一副三角板不能画出;
135°角可以用一幅三角板中的直角和90°角或45°角画。
故选:C.
【点睛】本题考查了利用一副三角板画出的特殊角,找出规律是解决此类题的最好方法,应让学生记住凡是能用一副三角板画出的角的度数都是15°的整数倍.
5.C
【分析】钟表的一周,分成12个大格,求出每个大格的度数是,根据时针与分诊的格数解答即可.
【详解】解:.
故选C.
【点睛】此题考查了钟面角的有关知识,得出钟表上从1到12一共有12格,每个大格是解决问题的关键.
6.B
【分析】根据方位角的定义解答即可.
【详解】根据方位角的概念,射线表示的方向是北偏西.
故选:B.
【点睛】本题考查了方位角的概念及表示方法,方位角是表示方向的角;以正北,正南方向为基准,来描述物体所处的方向.用方位角描述方向时,通常以正北或正南方向为角的始边,以对象所处的射线为终边,故描述方位角时,一般先叙述北或南,再叙述偏东或偏西,偏多少度.(注意几个方向的角平分线按日常习惯,即东北,东南,西北,西南.)
7.B
【分析】根据题意可得:,然后利用角的和差关系可得,再根据方向角的定义即可解答.
【详解】解:如图,
∵学校A在小明家B北偏东的方向上,
∴,
∵,
∴,
∴超市C在小明家B的北偏西的方向上,
故选:B.
【点睛】此题主要考查了方向角的定义,正确根据图形得出的度数是解题关键.
8.
【分析】根据题意可知图中有两条射线,进而可得图中角的数量为个.
【详解】解:∵图中有两条射线,
∴图中角的数量为个,
故答案为:.
【点睛】本题考查了根据角中射线的数量求角的个数,根据图形找出规律是解题的关键.
9. 钝角 直角 锐角
【分析】根据角的分类解答即可.
【详解】解:由题意可知:角可以分成钝角,直角和锐角.
故答案为:钝角,直角,锐角
【点睛】本题考查角的分类,解题的关键是理解角的分类.
10./度
【分析】由钟面被等分成12份,每一份,再根据9点30分,时钟的时针和分针相距份,从而可得答案.
【详解】解:21点30分就是晚上9点30分,
9点30分,时钟的时针和分针相距(份),
9点30分,时钟的时针和分针所构成的夹角度数为.
故答案为:.
【点睛】本题考查的是时针与分针的夹角问题,理解钟面被等分12份,每一份是是解本题的关键.
11. 北 东 4
【分析】如图,根据圆的基本性质求出和的长度,再根据方位角的概念得出答案.
【详解】解:如图,连接,
由题意得:,
因为圆的直径是8米,
所以米,
所以点A在点O的北偏东方向4米处.
故答案为:北,东,30,4.
【点睛】本题主要考查了方位角,熟知方位角的表示方法是解题的关键.
12./40度
【分析】根据方位角的概念,画图正确表示出方位角,即可求解.
【详解】解:如图,由已知可得:,,
∵,
∴,
∴.
故答案为:.
【点睛】本题考查了方向角,熟练根据题目的已知条件并结合图形分析是解题的关键.
13.(1),,,共3个
(2),
(3),,共2个
【分析】(1)根据角的表示方法写出答案;
(2)根据角的定义和角的表示方法写出答案;
(3)角的表示方法写出答案.
【详解】(1)解:以点为顶点的角:,,,共3个;
(2)以射线为边的角:,;
(3)以为顶点,为一边的角有:,,共2个.
【点睛】此题主要考查了角的概念,关键是掌握角的表示方法.
14.(1)
(2)
(3),
【分析】(1)根据角的表示方法进行求解即可;
(2)根据角的表示方法进行求解即可;
(3)根据角的表示方法进行求解即可.
【详解】(1)解:能用一个大写字母表示的角为
(2)解:由题意得,以点为顶点的角有;
(3)解:由题意得,图中所有小于平角的角有,.
【点睛】本题主要考查了角的表示方法,熟知角的表示方法是解题的关键.
15.(1)见解析
(2)见解析
(3)见解析
(4)见解析
【分析】(1)过画射线即可.
(2)连接B和C即可.
(3)分别以C为顶点画射线、即可.
(4)连接,与的交点就是P点位置,根据线段的性质:两点之间,线段距离最短;结合题意,要使它与四个村庄的距离之和最小,就要使他在与的交点处.
【详解】(1)解:如图所示:
(2)如图所示;
(3)如图所示;
(4)P点即为所求,
根据线段的性质:两点之间,线段距离最短;
结合题意,要使它与四个村庄的距离之和最小,就要使他在与的交点处.
【点睛】本题考查了射线,线段的性质:两点之间,线段距离最短.要求学生能灵活应用所学的知识,解决实际问题.
16.(1)北,600
(2)北,东,45,800
(3)见解析
【分析】(1)在地图上的方向为上北、下南、左西、右东,可以判定书书店在区政府正北方向,又由线段比例尺1厘米体表200米,书店距区政府3厘米,即可求出书店距区政府的实际距离.
(2)图书馆在区政府东偏北方向4厘米处,根据图中线段比例尺,即可求出图书馆距区政府的实际距离.
(3)由学校在区政府北偏西方向,600米处,根据图中线段比例尺可求出学校距区政府的图上距离.
【详解】(1)解:米,
书店在区政府的北面600米处;
(2)米,
图书馆在区政府的北偏东方向800米处;
(3)厘米,
画图如下:
【点睛】本题考查的知识点有:根据方向和距离确定物体的位置、在平面图上标出物体的位置,用线段比例尺求图上距离和实际距离.
17.
【分析】根据方向角的定义得到,,再求出,根据角的和差计算即可.
【详解】解:由题意可得:,,
∴,
又∵,
∴.
【点睛】本题考查方向角,理解方向角的定义以及角的和差关系是正确解答的前提.
21世纪教育网(www.21cnjy.com)
人教版七年级数学上册 4.3.1 角 导学案
【知识清单】
角:由两条具有公共端点引出射线组成的图形(也可看做是由一射线绕端点旋转而成)。
角的表示:三个大写字母;一个大写字母(不混淆情况下方可使用);一个数字;一个希腊字母。
角的要素:顶点和边,角的大小与边的长短无关。
【典型例题】
考点1:角的概念理解
例1.下列说法中正确的是( )
A.两条射线组成的图形叫做角 B.两点之间直线最短
C.两点确定一条直线 D.若,则点B是的中点
【答案】C
【分析】根据两点确定一条直线,角的定义,线段中点的定义对各选项分析判断后利用排除法求解.
【详解】A、应为有公共端点的两条射线组成的图形叫做角,故本选项错误;
B、应为两点之间线段最短,故本选项错误;
C、两点确定一条直线正确,故本选项正确;
D、若,则点为的中点错误,因为、、三点不一定共线,故本选项错误.
故选:C.
【点睛】本题考查了线段的性质,直线的性质,以及角的定义,是基础题,熟记概念与各性质是解题的关键.
考点2:角的表示方法
例2.下列四个图中,能用三种方法表示同一个角的是( )
A. B.
C. D.
【答案】D
【分析】根据角的表示方法和图形选出即可.
【详解】解:A、图中的不能用表示,故本选项错误;
B、图中的和不是表示同一个角,故本选项错误;
C、图中的和不是表示同一个角,故本选项错误;
D、图中、、表示同一个角,故本选项正确;
故选:D.
【点睛】本题考查了角的表示方法的应用,主要考查学生的理解能力和观察图形的能力.
.
故选:.
【点睛】本题主要考查了方向角,用方向角描述方向时,通常以正北或正南方向为角的始边,以对象所处的射线为终边,故描述方向角时,一般先叙述北或南,再叙述偏东或偏西.
考点3:角的分类
例3.下列说法正确的是( )
A.两点之间,直线最短 B.圆是立体图形
C.小于的角是锐角 D.射线与射线是同一条射线
【答案】C
【分析】根据线段、射线与两点之间的距离等性质依次判断即可.
【详解】解:A、两点之间线段最短,原说法错误,选项错误;
B、圆不是立体图形,原说法错误,选项错误;
C、小于的角是锐角,说法正确,选项正确;
D、射线与射线不是同一条射线,方向相反,原说法错误,选项错误,
故选:C.
【点睛】题目主要考查线段、射线、两点间的距离的性质,熟练掌握各个性质是解题关键.
考点4:画特殊角
例4.下列各度数的角,能借助一副三角尺画出的是( )
A.55° B.65° C.75° D.85°
【答案】C
【分析】一副三角板,度数有:、、、,根据度数组合,可以得到答案.
【详解】解:利用一副三角板可以画出的角,是和角的组合
故选:C.
【点睛】本题考查特殊角的画法,审题清晰是解题关键.
考点5:钟面角
例5.7点分,时钟的时针与分针的夹角为( )
A. B. C. D.
【答案】D
【分析】根据时钟上一大格是,进行计算即可解答.
【详解】解:由题意得:,
故选:D.
【点睛】本题考查了钟面角,熟练掌握时钟上一大格是是解题的关键.
考点6:方向角的表示
例6.观察点不变,观察角度变小,观察的范围( )
A.变小 B.变大 C.不变 D.不确定
【答案】A
【分析】观察点变近,观察的角度不变观察的范围就会变小.观察点不变角度越小,观察的范围就越小.
【详解】解:观察点不变,观察角度变小,观察的范围变小;
故选:A.
【点睛】本题主要考查了观察点,观察角度,观察范围三者之间的关系.
考点7:与方向角有关的计算题
例7.点在点的北偏东度,点在点的西偏北度,则的度数为( )
A. B. C. D.
【答案】B
【分析】点在点的北偏东度,点在点的西偏北度,画图即可得到的度数.
【详解】解:如图,点在点的北偏东度,点在点的西偏北度,
【巩固提升】
1.用一个10倍的放大镜看一个的角,看到的角的度数为( )
A. B. C. D.
2.如图,能用,,三种方法表示同一个角的是( )
A. B.
C. D.
3.下列标注的四个角中,最小的角是( )
A. B. C. D.
4.用一副三角板不能画出的角是( ).
A.75° B.105° C.110° D.135°
5.上午时,钟表的分针与时针夹角的度数是( )
A.105度 B.85度 C.95度 D.115度
6.如图,关于射线所指方向描述正确的是( )
A.东偏北 B.北偏西 C.西偏北 D.南偏西
7.如图,学校A在小明家B北偏东的方向上,点C表示超市所在的位置,,则超市C在小明家B的( )
A.北偏西的方向上 B.北偏西的方向上
C.南偏西的方向上 D.南偏东的方向上
二、填空题
8.如图,则图中共有 个角.
9.角可以分为 、 、 三类.
10.当时间为时,时针和分针所夹角度为 .
11.如图,把一个直径8米的圆平均分成四个扇形,再把每个扇形的弧三等分.点A在点O的 偏 °方向 米处.
12.如图,轮船从出发向北偏东方向航行一段时间到达,又从出发向南偏西方向航行一段时间到达,则 .
三、解答题
13.如图:
(1)以点B为顶点的角有几个?分别表示出来.
(2)请分别指出以射线为边的角.
(3)以D为顶点,为一边的角有几个?分别写出来.
14.写出图中符合下列条件的角.
(1)能用一个大写字母表示的角;
(2)以点为顶点的角;
(3)图中所有小于平角的角(可用简便方法表示).
15.画图,说理题
如图,已知四个点A、B、C、D;
(1)画射线;
(2)画线段;
(3)画;
(4)画出一点P,使P到点A、B、C、D的距离之和最小,并说明理由.
16.按要求解答下面各题.
(1)书店在区政府的( )面( )米处.
(2)图书馆在区政府的( )偏( )( )方向( )米处.
(3)学校在区政府北偏西方向600米处,请列式计算并在图上标出.
17.如图,射线表示的方向是北偏东,射线表示的方向是北偏西,射线在射线和射线之间,且.求的度数.
参考答案
1.D
【分析】把角按一定比例放大或缩小,角的度数不变.
【详解】解:放大镜看一个的角,角的两边的张开程度没变,即角的度数不变,
故选:D.
【点睛】本题考查角的概念,关键是掌握图形的放大或缩小的性质.
2.C
【分析】角的表示方法有三种:(1)用三个字母及符号“”来表示.中间的字母表示顶点,其它两个字母分别表示角的两边上的点.(2)用一个数字表示一个角.(3)用一个字母表示一个角.具体用哪种方法,要根据角的情况进行具体分析,总之表示要明确,不能使人产生误解.
【详解】解:在选项A、B、D中,如果用表示,容易使人产生歧义,
无法让人明确到底表示哪个角;
只有选项C能用,,三种方法表示同一个角,不会使人产生歧义.
故选:C.
【点睛】此题主要考查学生对角的概念和角的表示方法的理解和掌握.通过练习,使学生学会角的表示方法,为今后的学习奠定基础.
3.B
【分析】根据角的分类即可得.
【详解】解:A是钝角,大于小于;B是锐角,小于;C是直角,等于;D是平角,等于,
∴最小的角是锐角,
故选:B.
【点睛】本题考查了角的分类和比较大小,解题的关键是掌握角的分类.
4.C
【分析】105°=60°+45°,105°角可以用一幅三角板中的60°角和45°角画;75°=45°+30°,75°角可以用一幅三角板中的45°角和30°角画;135°=90°+45°,135°角可以用一幅三角板中的直角和90°角或45°角画;110°角用一副三角板不能画出.
【详解】解:105°角可以用一幅三角板中的60°角和45°角画;
75°角可以用一幅三角板中的45°角和30°角画;
110°角用一副三角板不能画出;
135°角可以用一幅三角板中的直角和90°角或45°角画。
故选:C.
【点睛】本题考查了利用一副三角板画出的特殊角,找出规律是解决此类题的最好方法,应让学生记住凡是能用一副三角板画出的角的度数都是15°的整数倍.
5.C
【分析】钟表的一周,分成12个大格,求出每个大格的度数是,根据时针与分诊的格数解答即可.
【详解】解:.
故选C.
【点睛】此题考查了钟面角的有关知识,得出钟表上从1到12一共有12格,每个大格是解决问题的关键.
6.B
【分析】根据方位角的定义解答即可.
【详解】根据方位角的概念,射线表示的方向是北偏西.
故选:B.
【点睛】本题考查了方位角的概念及表示方法,方位角是表示方向的角;以正北,正南方向为基准,来描述物体所处的方向.用方位角描述方向时,通常以正北或正南方向为角的始边,以对象所处的射线为终边,故描述方位角时,一般先叙述北或南,再叙述偏东或偏西,偏多少度.(注意几个方向的角平分线按日常习惯,即东北,东南,西北,西南.)
7.B
【分析】根据题意可得:,然后利用角的和差关系可得,再根据方向角的定义即可解答.
【详解】解:如图,
∵学校A在小明家B北偏东的方向上,
∴,
∵,
∴,
∴超市C在小明家B的北偏西的方向上,
故选:B.
【点睛】此题主要考查了方向角的定义,正确根据图形得出的度数是解题关键.
8.
【分析】根据题意可知图中有两条射线,进而可得图中角的数量为个.
【详解】解:∵图中有两条射线,
∴图中角的数量为个,
故答案为:.
【点睛】本题考查了根据角中射线的数量求角的个数,根据图形找出规律是解题的关键.
9. 钝角 直角 锐角
【分析】根据角的分类解答即可.
【详解】解:由题意可知:角可以分成钝角,直角和锐角.
故答案为:钝角,直角,锐角
【点睛】本题考查角的分类,解题的关键是理解角的分类.
10./度
【分析】由钟面被等分成12份,每一份,再根据9点30分,时钟的时针和分针相距份,从而可得答案.
【详解】解:21点30分就是晚上9点30分,
9点30分,时钟的时针和分针相距(份),
9点30分,时钟的时针和分针所构成的夹角度数为.
故答案为:.
【点睛】本题考查的是时针与分针的夹角问题,理解钟面被等分12份,每一份是是解本题的关键.
11. 北 东 4
【分析】如图,根据圆的基本性质求出和的长度,再根据方位角的概念得出答案.
【详解】解:如图,连接,
由题意得:,
因为圆的直径是8米,
所以米,
所以点A在点O的北偏东方向4米处.
故答案为:北,东,30,4.
【点睛】本题主要考查了方位角,熟知方位角的表示方法是解题的关键.
12./40度
【分析】根据方位角的概念,画图正确表示出方位角,即可求解.
【详解】解:如图,由已知可得:,,
∵,
∴,
∴.
故答案为:.
【点睛】本题考查了方向角,熟练根据题目的已知条件并结合图形分析是解题的关键.
13.(1),,,共3个
(2),
(3),,共2个
【分析】(1)根据角的表示方法写出答案;
(2)根据角的定义和角的表示方法写出答案;
(3)角的表示方法写出答案.
【详解】(1)解:以点为顶点的角:,,,共3个;
(2)以射线为边的角:,;
(3)以为顶点,为一边的角有:,,共2个.
【点睛】此题主要考查了角的概念,关键是掌握角的表示方法.
14.(1)
(2)
(3),
【分析】(1)根据角的表示方法进行求解即可;
(2)根据角的表示方法进行求解即可;
(3)根据角的表示方法进行求解即可.
【详解】(1)解:能用一个大写字母表示的角为
(2)解:由题意得,以点为顶点的角有;
(3)解:由题意得,图中所有小于平角的角有,.
【点睛】本题主要考查了角的表示方法,熟知角的表示方法是解题的关键.
15.(1)见解析
(2)见解析
(3)见解析
(4)见解析
【分析】(1)过画射线即可.
(2)连接B和C即可.
(3)分别以C为顶点画射线、即可.
(4)连接,与的交点就是P点位置,根据线段的性质:两点之间,线段距离最短;结合题意,要使它与四个村庄的距离之和最小,就要使他在与的交点处.
【详解】(1)解:如图所示:
(2)如图所示;
(3)如图所示;
(4)P点即为所求,
根据线段的性质:两点之间,线段距离最短;
结合题意,要使它与四个村庄的距离之和最小,就要使他在与的交点处.
【点睛】本题考查了射线,线段的性质:两点之间,线段距离最短.要求学生能灵活应用所学的知识,解决实际问题.
16.(1)北,600
(2)北,东,45,800
(3)见解析
【分析】(1)在地图上的方向为上北、下南、左西、右东,可以判定书书店在区政府正北方向,又由线段比例尺1厘米体表200米,书店距区政府3厘米,即可求出书店距区政府的实际距离.
(2)图书馆在区政府东偏北方向4厘米处,根据图中线段比例尺,即可求出图书馆距区政府的实际距离.
(3)由学校在区政府北偏西方向,600米处,根据图中线段比例尺可求出学校距区政府的图上距离.
【详解】(1)解:米,
书店在区政府的北面600米处;
(2)米,
图书馆在区政府的北偏东方向800米处;
(3)厘米,
画图如下:
【点睛】本题考查的知识点有:根据方向和距离确定物体的位置、在平面图上标出物体的位置,用线段比例尺求图上距离和实际距离.
17.
【分析】根据方向角的定义得到,,再求出,根据角的和差计算即可.
【详解】解:由题意可得:,,
∴,
又∵,
∴.
【点睛】本题考查方向角,理解方向角的定义以及角的和差关系是正确解答的前提.
21世纪教育网(www.21cnjy.com)
