21.3实际问题与一元二次方程第2课时关于图形问题的应用题课后作业(含答案)
文档属性
| 名称 | 21.3实际问题与一元二次方程第2课时关于图形问题的应用题课后作业(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 584.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-06 19:46:26 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
21.3实际问题与一元二次方程
第2课时关于图形问题的应用题
1.某学校准备修建一个面积为200 m 的矩形花圃,它的长比宽多10 m,设花圃的宽为xm,则列出的正确方程为( )
A. x(x-10)=200
B.2x+2(x-10)=200
C. x(x+10)=200
D.2x+2(x+10)=200
2.把一个正方形的一边增加2cm,另一边增加1 cm,所得的长方形的面积比正方形面积增加 14 cm ,则原来正方形的边长是( )
A.3cmB.5cm
C.4 cmD.6 cm
3.王叔叔从市场上买了一块长为80 cm,宽为70 cm的矩形铁皮,准备制作一个工具箱.如图,他将矩形铁皮的四个角各剪掉一个边长xcm的正方形后,剩余的部分刚好能围成一个底面积为3 000 cm 的无盖长方体工具箱,根据题意列方程为( )
A.(80-x)(70-x)=3000
B.80×70-4x =3 000
C.(80-2x)(70-2x)=3000
D.80×70-4x -(70+80)x=3 000
4.某公园有一块正方形的空2m地,后来从这块空地上划出部分区域栽种鲜花(如图),原空地一边减少了1m,另
一边减少了2m,剩余空地的面积为18m ,求原正方形的边长.设原正方形空地的边长为xm,则列出的正确方程为( )
A.(x+1)(x+2)=18
B. x -3x+16=0
C.(x-1)(x-2)=18
D. x +3x+16=0
5.某校进行体操队列训练,原有8行10列,后增加40人,使得队伍增加的行数、列数相同,你知道增加了多少行或多少列吗 设增加了x行或列,则列方程得( )
A.(8-x)(10-x)=8×10-40
B.(8-x)(10-x)=8×10+40
C.(8+x)(10+x)=8×10-40
D.(8+x)(10+x)=8×10+40
6.如图,某小区计32m划在一块长为20m32m,宽为20 m 的矩形空地上修建三条同样宽的道路,剩余的空地上种植草
坪,使草坪的面积为570 m .若设道路的宽为xm,则下面所列方程正确的是( )
A.(32-2x)(20-x)=570
B.32x+2×20x=32×20-570
C.(32-x)(20-x)=32×20-570
D.32x+2×20x-2x =570
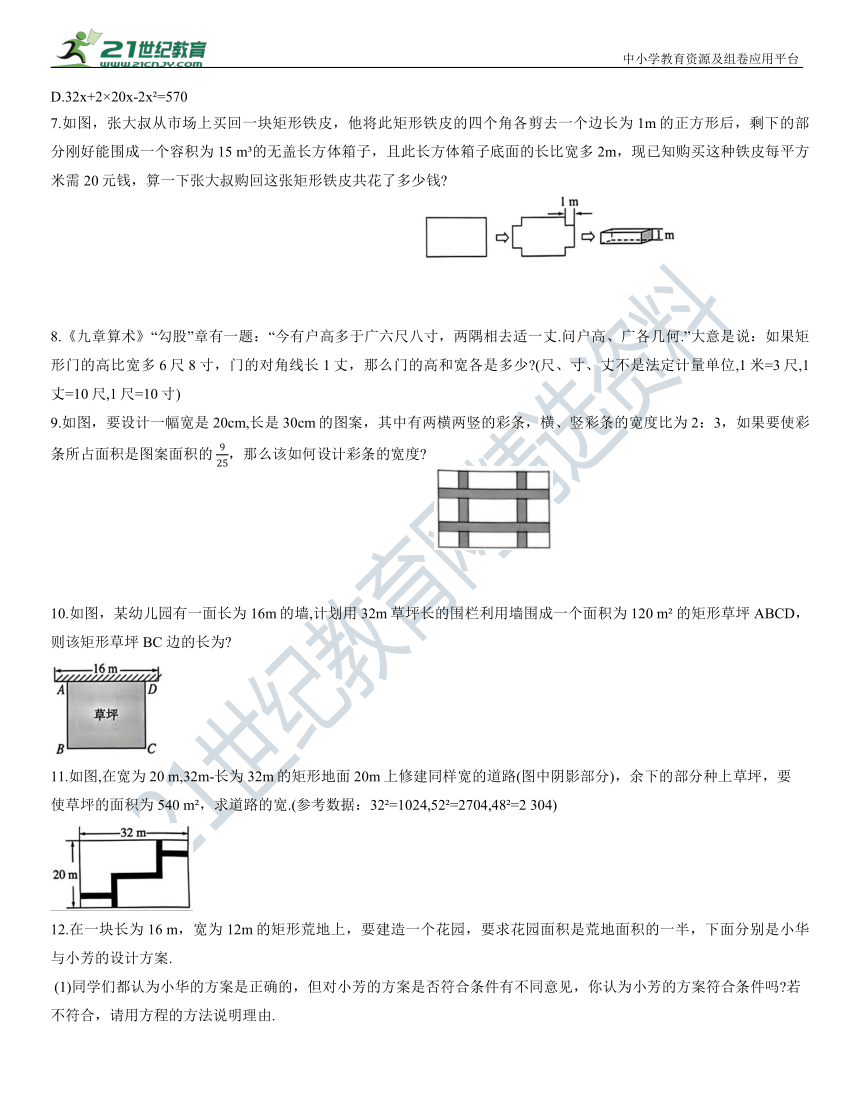
7.如图,张大叔从市场上买回一块矩形铁皮,他将此矩形铁皮的四个角各剪去一个边长为1m的正方形后,剩下的部分刚好能围成一个容积为15 m 的无盖长方体箱子,且此长方体箱子底面的长比宽多2m,现已知购买这种铁皮每平方米需20元钱,算一下张大叔购回这张矩形铁皮共花了多少钱
8.《九章算术》“勾股”章有一题:“今有户高多于广六尺八寸,两隅相去适一丈.问户高、广各几何.”大意是说:如果矩形门的高比宽多6尺8寸,门的对角线长1丈,那么门的高和宽各是多少 (尺、寸、丈不是法定计量单位,1米=3尺,1丈=10尺,1尺=10寸)
9.如图,要设计一幅宽是20cm,长是30cm的图案,其中有两横两竖的彩条,横、竖彩条的宽度比为2:3,如果要使彩条所占面积是图案面积的 ,那么该如何设计彩条的宽度
10.如图,某幼儿园有一面长为16m的墙,计划用32m草坪长的围栏利用墙围成一个面积为 120 m 的矩形草坪ABCD,则该矩形草坪BC 边的长为
11.如图,在宽为 20 m,32m-长为32m的矩形地面20m上修建同样宽的道路(图中阴影部分),余下的部分种上草坪,要
使草坪的面积为540 m ,求道路的宽.(参考数据:32 =1024,52 =2704,48 =2 304)
12.在一块长为16 m,宽为12m的矩形荒地上,要建造一个花园,要求花园面积是荒地面积的一半,下面分别是小华与小芳的设计方案.
(1)同学们都认为小华的方案是正确的,但对小芳的方案是否符合条件有不同意见,你认为小芳的方案符合条件吗 若
不符合,请用方程的方法说明理由.
(2)你还有其他的设计方案吗 请在图③中画出你所设计的草图,将花园部分涂上阴影,并加以说明.
C 2. C 3. C4. C 5. D 6. A
7.解设这种长方体箱子底部宽为xm,则长为(x+2)m.
依题意,有x(x+2)×1=15.
整理,得x +2x-15=0,
解得x =-5(舍去),x =3,所以x+2=5.
由长方体展开图可知,所购买矩形铁皮面积为(5+2)×(3+2)=35(m ).
因此张大叔购回这张矩形铁皮共花了 35×20=700(元).
8.解设门高x尺,则宽为(x-6.8)尺,根据题意,得 10 =x +(x-6.8) ,解得x=9.6.x-6.8=2.8(尺).
故门的高和宽各是9尺6寸、2尺8寸.
9. 解:设横彩条的宽度是2xcm,则竖彩条的宽度是3x cm.根据题意可得(30-6x)(20- 解得x =1,x =9.
∵4×9=36>20,
∴x=9舍去.
∴横彩条的宽度是2cm,竖彩条的宽度是3c m.
10. 12m
11. 设道路宽为xm,根据题意,
得20×32-(20+32)x+x =540,整理得x -52x+
100=0,解得x =2,x =50((不合题意,舍去).
故道路宽为 2m.
12.解(1)不符合.
设小路宽度均为xm,根据题意,得(16-2x)(12- 解这个方程,得x =2,x =12.
但x =12不符合题意,应舍去,所以x=2.
故小芳的方案不符合条件,小路的宽度应为2m.
(2)答案不唯一.
21.3实际问题与一元二次方程
第2课时关于图形问题的应用题
1.某学校准备修建一个面积为200 m 的矩形花圃,它的长比宽多10 m,设花圃的宽为xm,则列出的正确方程为( )
A. x(x-10)=200
B.2x+2(x-10)=200
C. x(x+10)=200
D.2x+2(x+10)=200
2.把一个正方形的一边增加2cm,另一边增加1 cm,所得的长方形的面积比正方形面积增加 14 cm ,则原来正方形的边长是( )
A.3cmB.5cm
C.4 cmD.6 cm
3.王叔叔从市场上买了一块长为80 cm,宽为70 cm的矩形铁皮,准备制作一个工具箱.如图,他将矩形铁皮的四个角各剪掉一个边长xcm的正方形后,剩余的部分刚好能围成一个底面积为3 000 cm 的无盖长方体工具箱,根据题意列方程为( )
A.(80-x)(70-x)=3000
B.80×70-4x =3 000
C.(80-2x)(70-2x)=3000
D.80×70-4x -(70+80)x=3 000
4.某公园有一块正方形的空2m地,后来从这块空地上划出部分区域栽种鲜花(如图),原空地一边减少了1m,另
一边减少了2m,剩余空地的面积为18m ,求原正方形的边长.设原正方形空地的边长为xm,则列出的正确方程为( )
A.(x+1)(x+2)=18
B. x -3x+16=0
C.(x-1)(x-2)=18
D. x +3x+16=0
5.某校进行体操队列训练,原有8行10列,后增加40人,使得队伍增加的行数、列数相同,你知道增加了多少行或多少列吗 设增加了x行或列,则列方程得( )
A.(8-x)(10-x)=8×10-40
B.(8-x)(10-x)=8×10+40
C.(8+x)(10+x)=8×10-40
D.(8+x)(10+x)=8×10+40
6.如图,某小区计32m划在一块长为20m32m,宽为20 m 的矩形空地上修建三条同样宽的道路,剩余的空地上种植草
坪,使草坪的面积为570 m .若设道路的宽为xm,则下面所列方程正确的是( )
A.(32-2x)(20-x)=570
B.32x+2×20x=32×20-570
C.(32-x)(20-x)=32×20-570
D.32x+2×20x-2x =570
7.如图,张大叔从市场上买回一块矩形铁皮,他将此矩形铁皮的四个角各剪去一个边长为1m的正方形后,剩下的部分刚好能围成一个容积为15 m 的无盖长方体箱子,且此长方体箱子底面的长比宽多2m,现已知购买这种铁皮每平方米需20元钱,算一下张大叔购回这张矩形铁皮共花了多少钱
8.《九章算术》“勾股”章有一题:“今有户高多于广六尺八寸,两隅相去适一丈.问户高、广各几何.”大意是说:如果矩形门的高比宽多6尺8寸,门的对角线长1丈,那么门的高和宽各是多少 (尺、寸、丈不是法定计量单位,1米=3尺,1丈=10尺,1尺=10寸)
9.如图,要设计一幅宽是20cm,长是30cm的图案,其中有两横两竖的彩条,横、竖彩条的宽度比为2:3,如果要使彩条所占面积是图案面积的 ,那么该如何设计彩条的宽度
10.如图,某幼儿园有一面长为16m的墙,计划用32m草坪长的围栏利用墙围成一个面积为 120 m 的矩形草坪ABCD,则该矩形草坪BC 边的长为
11.如图,在宽为 20 m,32m-长为32m的矩形地面20m上修建同样宽的道路(图中阴影部分),余下的部分种上草坪,要
使草坪的面积为540 m ,求道路的宽.(参考数据:32 =1024,52 =2704,48 =2 304)
12.在一块长为16 m,宽为12m的矩形荒地上,要建造一个花园,要求花园面积是荒地面积的一半,下面分别是小华与小芳的设计方案.
(1)同学们都认为小华的方案是正确的,但对小芳的方案是否符合条件有不同意见,你认为小芳的方案符合条件吗 若
不符合,请用方程的方法说明理由.
(2)你还有其他的设计方案吗 请在图③中画出你所设计的草图,将花园部分涂上阴影,并加以说明.
C 2. C 3. C4. C 5. D 6. A
7.解设这种长方体箱子底部宽为xm,则长为(x+2)m.
依题意,有x(x+2)×1=15.
整理,得x +2x-15=0,
解得x =-5(舍去),x =3,所以x+2=5.
由长方体展开图可知,所购买矩形铁皮面积为(5+2)×(3+2)=35(m ).
因此张大叔购回这张矩形铁皮共花了 35×20=700(元).
8.解设门高x尺,则宽为(x-6.8)尺,根据题意,得 10 =x +(x-6.8) ,解得x=9.6.x-6.8=2.8(尺).
故门的高和宽各是9尺6寸、2尺8寸.
9. 解:设横彩条的宽度是2xcm,则竖彩条的宽度是3x cm.根据题意可得(30-6x)(20- 解得x =1,x =9.
∵4×9=36>20,
∴x=9舍去.
∴横彩条的宽度是2cm,竖彩条的宽度是3c m.
10. 12m
11. 设道路宽为xm,根据题意,
得20×32-(20+32)x+x =540,整理得x -52x+
100=0,解得x =2,x =50((不合题意,舍去).
故道路宽为 2m.
12.解(1)不符合.
设小路宽度均为xm,根据题意,得(16-2x)(12- 解这个方程,得x =2,x =12.
但x =12不符合题意,应舍去,所以x=2.
故小芳的方案不符合条件,小路的宽度应为2m.
(2)答案不唯一.
同课章节目录
