2.2 基本不等式——2023-2024学年高一数学人教A版(2019)必修第一册课时分层练(含答案)
文档属性
| 名称 | 2.2 基本不等式——2023-2024学年高一数学人教A版(2019)必修第一册课时分层练(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 356.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-06 00:00:00 | ||
图片预览



文档简介
2.2 基本不等式
【夯实基础】
知识点1 基本不等式
1.已知正数a,b满足,则有( )
A.最小值 B.最小值 C.最大值 D.最大值
2.已知,,,若不等式恒成立,则m的最大值为( )
A.1 B.2 C.3 D.7
3.已知,则的最小值是_________.
4.若,,则的最小值为__________.
知识点2 基本不等式的应用
5.如果,,,,那么P,Q,M的大小顺序是( )
A. B. C. D.
6.在使成立的所有常数M中,我们把M的最小值叫做的上确界,若,,且,则的上确界为( )
A.-3 B.-4 C. D.
7.某公司一年购买某种货物900吨,每次都购买x吨,运费为3万元/次,一年的总存储费用为3x万元,若要使一年的总运费与总存储费用之和最小,则每次需购买( )
A.20 B.30 C.40 D.60
8.若正数a,b满足,则的取值范围是_________.
【提升能力】
9.已知,且,则的最小值为( )
A.3 B.4 C.6 D.9
10.已知正数x,y满足,则的最小值为( )
A.2 B. C. D.5
11.(多选)已知,,,则( )
A. B. C. D.
12.(多选)下列结论正确的是( )
A.若a,b为正实数,且,则
B.若a,b,m为正实数,且,则
C.若,则
D.当时,的最小值为2
13.已知,,,则的最小值为__________.
14.已知,,且,则的最小值为_________.
【综合素养】
15.已知正实数x,y满足,且恒成立,则t的取值范围是___________.
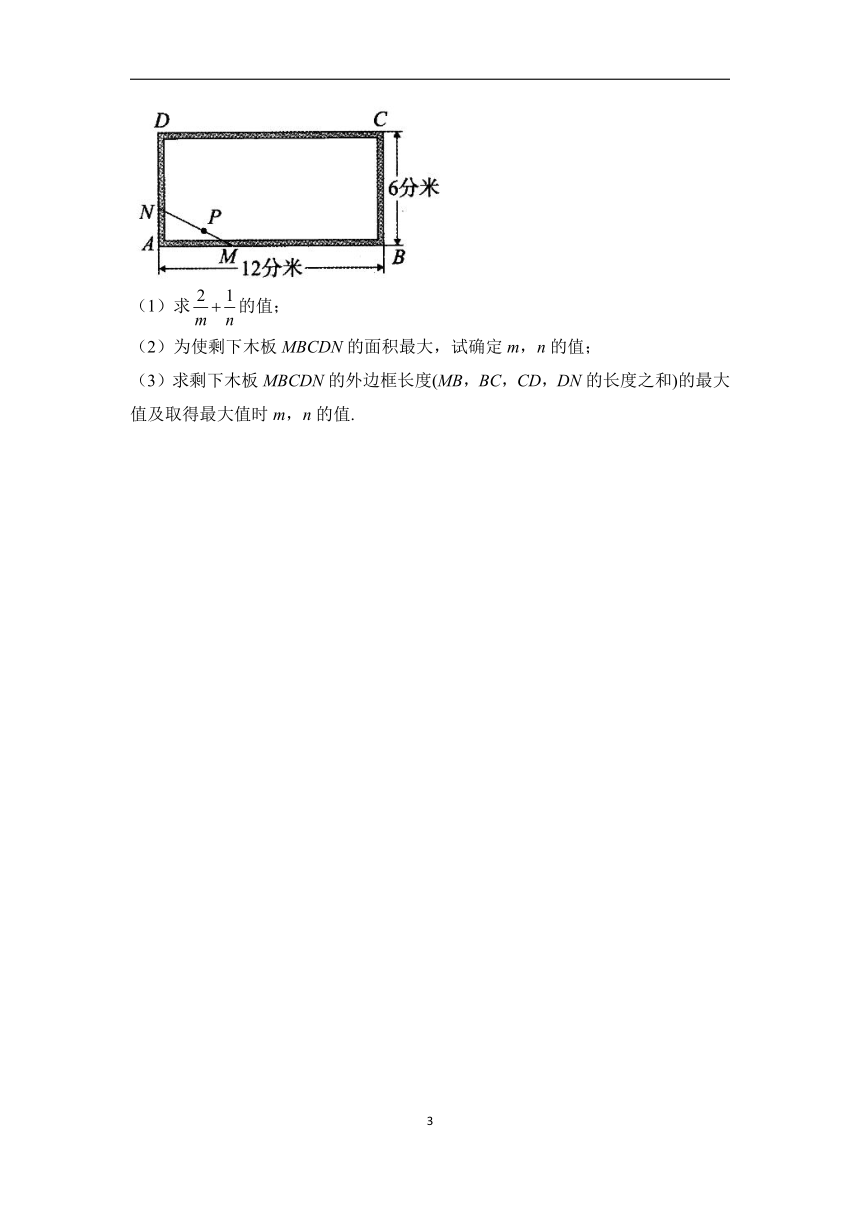
16.如图,长方形ABCD表示一张(单位:分米)的工艺木板,其四周有边框(图中阴影部分),中间为薄板.木板上一瑕 (记为点P)到外边框AB,AD的距离分别为1分米、2分米.现欲经过点P锯掉一块三角形废料MAN,其中M,N分别在AB,AD上.设AM,AN的长分别为m分米、n分米.
(1)求的值;
(2)为使剩下木板MBCDN的面积最大,试确定m,n的值;
(3)求剩下木板MBCDN的外边框长度(MB,BC,CD,DN的长度之和)的最大值及取得最大值时m,n的值.
答案以及解析
1.答案:C
解析:正数a,b满足,,当且仅当时取等号,即有最大值,故选C.
2.答案:C
解析:因为,所以.又因为,,所以,当且仅当时取等号.由题意可得,即,则m的最大值为3.故选C.
3.答案:5
解析:由题意可得,当且仅当,即时,等号成立.
4.答案:
解析:因为,,所以,当且仅当且,即时等号成立,所以的最小值为.
5.答案:B
解析:依题意,根据基本不等式可知.因为,,所以,,所以,即.故选B.
6.答案:D
解析:根据题意,由,得.因为,,所以,当且仅当,即时,等号成立,因此,所以根据定义知,的上确界为,故选D.
7.答案:B
解析:某公司一年购买某种货物900吨,每次都购买x吨,则需购买次,运费为3万元/次,一年的总存储费用为3x万元,则一年的总运费与总存储费用之和为,当且仅当,即吨时,等号成立,所以每次购买30吨时,一年的总运费与总存储费用之和最小.故选B.
8.答案:
解析:解:,
因为正数a,b满足,所以,所以.
9.答案:A
解析:因为,所以,所以,当且仅当时,等号成立,故的最小值为3.选A.
10.答案:B
解析:因为,所以,
所以,
所以,
当且仅当即当时,等号成立,因此,的最小值为.故选B.
11.答案:ACD
解析:因为,,,,所以,当且仅当时,等号成立,故A正确,B错误;,因为,所以,故C正确;,因为,所以,故D正确.故选ACD.
12.答案:AC
解析:若a,b为正实数,且,则,即,故A正确;若a,b,m为正实数,且,则,即,故B错误;因为,所以,所以,故C正确;当时,,当且仅当时取等号,故D错误.选AC.
13.答案:
解析:因为,,,所以,当且仅当,即或时取等号,所以的最小值为.
14.答案:4
解析:,,.,,当且仅当时取等号,即,或,时,等号成立.
15.答案:或
解析:由,得.因为,所以,所以,,当且仅当时,等号成立,故.因为恒成立,所以,解得或.故t的取值范围是或.
16、(1)答案:
解析:如图,过点P分别作AB,AD的垂线,垂足分别为E,F,
则可得,所以,
即,整理可得.
(2)答案:当,时,剩下木板的面积最大
解析:要使剩下木板的面积最大,即要锯掉的三角形废料MAN的面积最小.
因为,,
所以,可得,
当且仅当,即,时,等号成立,
所以当,时,剩下木板的面积最大.
(3)答案:剩下木板的外边框长度的最大值为分米;分米,分米
解析:要使剩下木板的外边框长度最大,则锯掉的边框长度最小.
,
当且仅当,即,时等号成立,
故此时剩下木板的外边框长度的最大值为(分米),
此时分米,分米.
2
【夯实基础】
知识点1 基本不等式
1.已知正数a,b满足,则有( )
A.最小值 B.最小值 C.最大值 D.最大值
2.已知,,,若不等式恒成立,则m的最大值为( )
A.1 B.2 C.3 D.7
3.已知,则的最小值是_________.
4.若,,则的最小值为__________.
知识点2 基本不等式的应用
5.如果,,,,那么P,Q,M的大小顺序是( )
A. B. C. D.
6.在使成立的所有常数M中,我们把M的最小值叫做的上确界,若,,且,则的上确界为( )
A.-3 B.-4 C. D.
7.某公司一年购买某种货物900吨,每次都购买x吨,运费为3万元/次,一年的总存储费用为3x万元,若要使一年的总运费与总存储费用之和最小,则每次需购买( )
A.20 B.30 C.40 D.60
8.若正数a,b满足,则的取值范围是_________.
【提升能力】
9.已知,且,则的最小值为( )
A.3 B.4 C.6 D.9
10.已知正数x,y满足,则的最小值为( )
A.2 B. C. D.5
11.(多选)已知,,,则( )
A. B. C. D.
12.(多选)下列结论正确的是( )
A.若a,b为正实数,且,则
B.若a,b,m为正实数,且,则
C.若,则
D.当时,的最小值为2
13.已知,,,则的最小值为__________.
14.已知,,且,则的最小值为_________.
【综合素养】
15.已知正实数x,y满足,且恒成立,则t的取值范围是___________.
16.如图,长方形ABCD表示一张(单位:分米)的工艺木板,其四周有边框(图中阴影部分),中间为薄板.木板上一瑕 (记为点P)到外边框AB,AD的距离分别为1分米、2分米.现欲经过点P锯掉一块三角形废料MAN,其中M,N分别在AB,AD上.设AM,AN的长分别为m分米、n分米.
(1)求的值;
(2)为使剩下木板MBCDN的面积最大,试确定m,n的值;
(3)求剩下木板MBCDN的外边框长度(MB,BC,CD,DN的长度之和)的最大值及取得最大值时m,n的值.
答案以及解析
1.答案:C
解析:正数a,b满足,,当且仅当时取等号,即有最大值,故选C.
2.答案:C
解析:因为,所以.又因为,,所以,当且仅当时取等号.由题意可得,即,则m的最大值为3.故选C.
3.答案:5
解析:由题意可得,当且仅当,即时,等号成立.
4.答案:
解析:因为,,所以,当且仅当且,即时等号成立,所以的最小值为.
5.答案:B
解析:依题意,根据基本不等式可知.因为,,所以,,所以,即.故选B.
6.答案:D
解析:根据题意,由,得.因为,,所以,当且仅当,即时,等号成立,因此,所以根据定义知,的上确界为,故选D.
7.答案:B
解析:某公司一年购买某种货物900吨,每次都购买x吨,则需购买次,运费为3万元/次,一年的总存储费用为3x万元,则一年的总运费与总存储费用之和为,当且仅当,即吨时,等号成立,所以每次购买30吨时,一年的总运费与总存储费用之和最小.故选B.
8.答案:
解析:解:,
因为正数a,b满足,所以,所以.
9.答案:A
解析:因为,所以,所以,当且仅当时,等号成立,故的最小值为3.选A.
10.答案:B
解析:因为,所以,
所以,
所以,
当且仅当即当时,等号成立,因此,的最小值为.故选B.
11.答案:ACD
解析:因为,,,,所以,当且仅当时,等号成立,故A正确,B错误;,因为,所以,故C正确;,因为,所以,故D正确.故选ACD.
12.答案:AC
解析:若a,b为正实数,且,则,即,故A正确;若a,b,m为正实数,且,则,即,故B错误;因为,所以,所以,故C正确;当时,,当且仅当时取等号,故D错误.选AC.
13.答案:
解析:因为,,,所以,当且仅当,即或时取等号,所以的最小值为.
14.答案:4
解析:,,.,,当且仅当时取等号,即,或,时,等号成立.
15.答案:或
解析:由,得.因为,所以,所以,,当且仅当时,等号成立,故.因为恒成立,所以,解得或.故t的取值范围是或.
16、(1)答案:
解析:如图,过点P分别作AB,AD的垂线,垂足分别为E,F,
则可得,所以,
即,整理可得.
(2)答案:当,时,剩下木板的面积最大
解析:要使剩下木板的面积最大,即要锯掉的三角形废料MAN的面积最小.
因为,,
所以,可得,
当且仅当,即,时,等号成立,
所以当,时,剩下木板的面积最大.
(3)答案:剩下木板的外边框长度的最大值为分米;分米,分米
解析:要使剩下木板的外边框长度最大,则锯掉的边框长度最小.
,
当且仅当,即,时等号成立,
故此时剩下木板的外边框长度的最大值为(分米),
此时分米,分米.
2
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
