4.5 函数的应用(二)——2023-2024学年高一数学人教A版(2019)必修第一册课时分层练(含答案)
文档属性
| 名称 | 4.5 函数的应用(二)——2023-2024学年高一数学人教A版(2019)必修第一册课时分层练(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 439.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-06 00:00:00 | ||
图片预览



文档简介
4.5 函数的应用(二)
【夯实基础】
知识点1 函数的零点与方程的解
1.设函数有5个零点,,,,,且对一切实数x均满足,则( )
A.8 B.10 C.16 D.20
2.方程的实数根所在的区间为( ).
A. B. C. D.
3.表示不超过x的最大整数,例如,.已知是方程的根,则( )
A.2 B.3 C.4 D.5
知识点2 用二分法求方程的近似解
4.某同学用二分法求方程在内近似解的过程中,设,且计算,,,则该同学在第二次应计算的函数值为( )
A. B. C. D.
5.已知函数在内有一个零点,要使零点的近似值的精确度为0.001,若只从二等分区间的角度来考虑,则对区间至少需要二等分( )
A.8次 B.9次 C.10次 D.11次
知识点3 函数模型的应用
6.一般来说,事物总是经过发生、发展、成熟三个阶段,每个阶段的发展速度各不相同,通常在发生阶段变化速度较为缓慢、在发展阶段变化速度加快、在成熟阶段变化速度又趋于缓慢,按照上述三个阶段发展规律得到的变化曲线称为生长曲线.美国生物学家和人口统计学家雷蒙德·皮尔提出一种能较好地描述生物生长规律的生长曲线,称为“皮尔曲线”,常用的“皮尔曲线”的函数解析式为(,,),,该函数也可以简化为(,,)的形式.已知描述的是一种果树的高度随着时间x(单位:年)的变化规律,若刚栽种时该果树的高为1m,经过一年,该果树的高为2.5m,则该果树的高度超过8m,至少需要( )
A.4年 B.3年 C.5年 D.2年
7.由于某地人们健康水平的不断提高,某种疾病的患病率正以每年20%的比例降低.若要求患病率低于当前患病率的,则至少需要经过___________时间.(参考数据:,)( )
A.4年 B.5年 C.6年 D.7年
8.某校学生在研究折纸实验中发现,当对折后纸张达到一定的厚度时,便不能继续对折了.在理想情况下,对折次数n与纸的长边(单位:cm)和厚度x(单位:)满足.根据以上信息,当某张纸对折完4次时,的最小值为_________.现有一张长边为30 cm,厚度为0.01 cm的矩形纸,该矩形纸最多能对折_________次.(参考数值:)
【提升能力】
9.随着智能手机的普及,抖音、快手、火山视频等短视频APP迅速窜红.针对这种现状,某文化传媒有限公司决定逐年加大短视频制作的资金投入,若该公司2019年投入短视频制作的资金为5000万元人民币,在此基础上,若以后每年的资金投入均比上一年增长8%,则该公司投入短视频制作的资金开始超过6900万元人民币的年份是( ).(参考数据:,,)
A.2023年 B.2024年 C.2025年 D.2026年
10.已知定义域为R的偶函数满足,当时,,则方程在区间上所有解的和为( ).
A.8 B.7 C.6 D.5
11.(多选)已知函数有三个不同的零点,则实数a的取值可以为( )
A.0 B. C.3 D.4
12.(多选)已知定义域为R的偶函数有4个零点,,,,并且当时,,则下列说法中正确的是( )
A.实数a的取值范围是
B.当时,
C.
D.的取值范围是
13.已知函数,则函数的零点为________.
14.某种干细胞在培养过程中,每30分钟分裂一次(由一个分裂成两个),这种干细胞由1个培养成1024个需经过________小时.
【综合素养】
15.已知定义在R上的函数满足,且当时,,当时,,则函数在上有_________个零点.
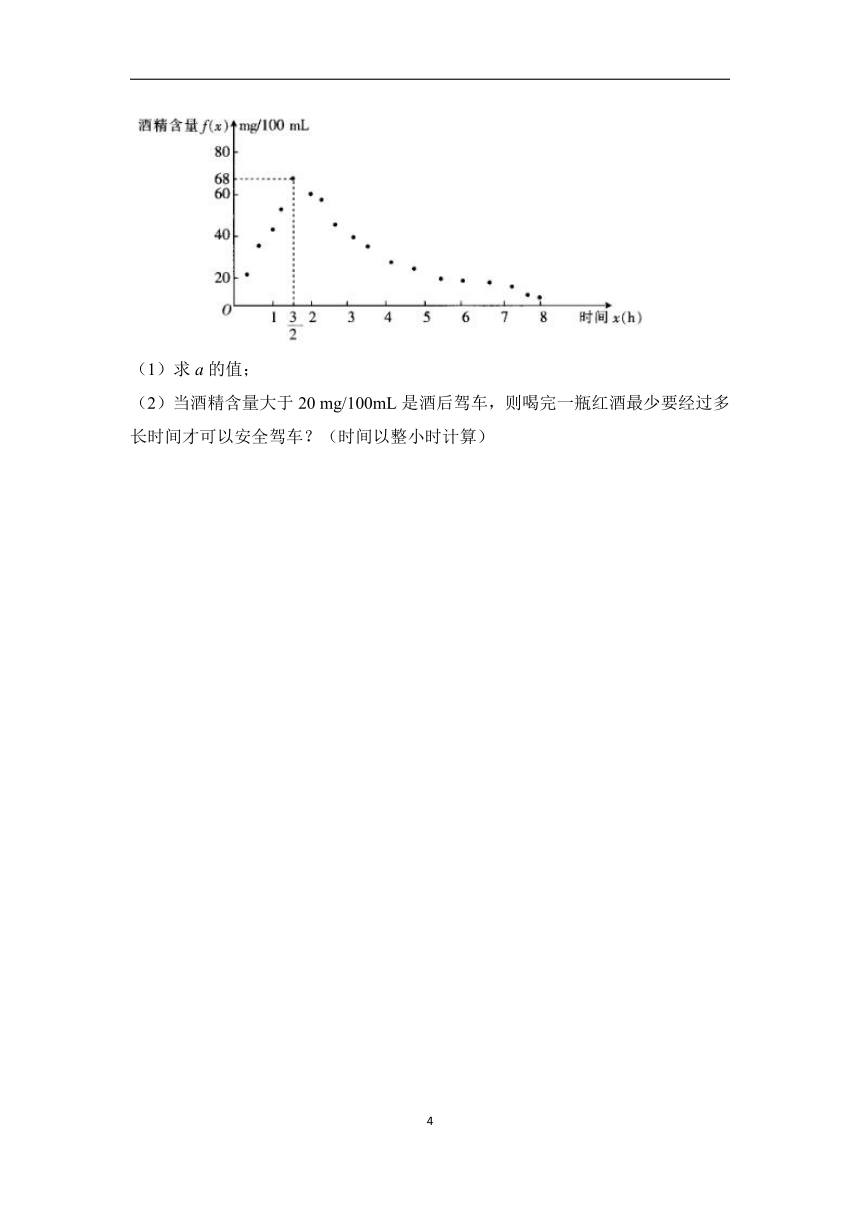
16.“半斤不脸红,一斤不心跳,二斤倒不了!”酒驾者都有超乎寻常的“自信”,显然他们已经忘记了酒精会使人神经麻痹、迟钝的真理.世界卫生组织的事故调查显示,在中国,每年由于酒后驾车引发的交通事故达数万起,而造成死亡的事故中50%以上都与酒后驾车有关,酒后驾车的危害触目惊心,已经成为交通事故的第一大“杀手”.经过反复试验,一般情况下,某人喝一瓶红酒后酒精在人体血液中的变化规律的“散点图”如图所示,且该图表示的函数模型为.
(1)求a的值;
(2)当酒精含量大于20 mg/100mL是酒后驾车,则喝完一瓶红酒最少要经过多长时间才可以安全驾车?(时间以整小时计算)
答案以及解析
1.答案:B
解析:对于任意,函数满足,函数的图像关于点对称,函数的零点关于直线对称,函数的5个零点中有2对关于直线对称,中间的零点是2,.故选B.
2.答案:A
解析:设,则,,因为,所以是方程的实数根所在的一个区间.又在R上单调递增,故方程有唯一的实数根.故选A.
3.答案:C
解析:令,
当时,,
当时,,
即,又单调递增,其图象是连续不断的,所以的零点所在区间为,所以,故选C.
4.答案:C
解析:,,,在区间(1,1.5)内函数存在一个零点,该同学在第二次应计算的函数值为.故选C.
5.答案:D
解析:本题考查二分法求方程近似值的过程.设对区间至少二等分n次,此时区间长度为2,则第n次二等分后区间长为,依题意得,,,所以.
6.答案:A
解析:由题可得则解得,,所以,由函数解析式可知,在上单调递增,且,,故该果树的高度超过8m,至少需要4年.故选A.
7.答案:B
解析:假设至少需要经过的时间为x(单位:年),由题意得,两边同时取以为底的对数得,.
因为,所以,即.故选B.
8.答案:64,7
解析:由,得,郎,
,即的最小值为64.
由题意知,
故该矩形纸最多能对折7次.
9.答案:B
解析:当年份为n时,短视频制作的资金为(万元),,,由,两边同时取对数并整理得,
解得,从而得,
所以资金投入开始超过6900万元的年份是2024年.故选B.
10.答案:A
解析:因为满足,所以,所以的图象关于直线对称,
令,则的图象关于直线对称,作出函数与在上的图象,如图所示.
由图知与的图象在区间上共有8个交点,且两两关于直线对称,所以方程在区间上所有解的和为,故选A.
11.答案:CD
解析:当时,恒成立,即在区间上无零点,所以当时,有三个正根,解得或.当时,单调递增,且,则方程有一个根,则方程要有两个根,即有两个正数解,则,解得,故C、D项正确.
12.答案:BC
解析:对于A选项,因为为偶函数且有4个零点,所以当时有2个零点,故,故A错误;对于B选项,当时,,故,故B正确;对于C选项,由函数是偶函数,可知,且,,故,故C正确;对于D选项,,由,可知,函数在上单调递增,故,故D错误.故选BC.
13.答案:-8和2
解析:令,得.
当时,令,得;当时,,易知在区间上单调递增,又,所以.
故函数的零点为-8和2.
14.答案:5
解析:干细胞分裂一次时有2个细胞,分裂2次时变为个细胞,分裂n次时变为个细胞,,所以分裂10次,每小时分裂2次,所以需要5小时.
15.答案:7
解析:由知是奇函数,又当时,,所以在上是周期为1的周期函数.令得,结合当时,,作出函数和的大致图象,如图所示,数形结合可知函数和的图象在上有7个交点,即函数在上有7个零点.
16.(1)答案:
解析:当时,,解得.
(2)答案:最少经过6小时才可以驾车
解析:由题意得,即,从而,解得,
所以最少经过6小时才可以驾车.
2
【夯实基础】
知识点1 函数的零点与方程的解
1.设函数有5个零点,,,,,且对一切实数x均满足,则( )
A.8 B.10 C.16 D.20
2.方程的实数根所在的区间为( ).
A. B. C. D.
3.表示不超过x的最大整数,例如,.已知是方程的根,则( )
A.2 B.3 C.4 D.5
知识点2 用二分法求方程的近似解
4.某同学用二分法求方程在内近似解的过程中,设,且计算,,,则该同学在第二次应计算的函数值为( )
A. B. C. D.
5.已知函数在内有一个零点,要使零点的近似值的精确度为0.001,若只从二等分区间的角度来考虑,则对区间至少需要二等分( )
A.8次 B.9次 C.10次 D.11次
知识点3 函数模型的应用
6.一般来说,事物总是经过发生、发展、成熟三个阶段,每个阶段的发展速度各不相同,通常在发生阶段变化速度较为缓慢、在发展阶段变化速度加快、在成熟阶段变化速度又趋于缓慢,按照上述三个阶段发展规律得到的变化曲线称为生长曲线.美国生物学家和人口统计学家雷蒙德·皮尔提出一种能较好地描述生物生长规律的生长曲线,称为“皮尔曲线”,常用的“皮尔曲线”的函数解析式为(,,),,该函数也可以简化为(,,)的形式.已知描述的是一种果树的高度随着时间x(单位:年)的变化规律,若刚栽种时该果树的高为1m,经过一年,该果树的高为2.5m,则该果树的高度超过8m,至少需要( )
A.4年 B.3年 C.5年 D.2年
7.由于某地人们健康水平的不断提高,某种疾病的患病率正以每年20%的比例降低.若要求患病率低于当前患病率的,则至少需要经过___________时间.(参考数据:,)( )
A.4年 B.5年 C.6年 D.7年
8.某校学生在研究折纸实验中发现,当对折后纸张达到一定的厚度时,便不能继续对折了.在理想情况下,对折次数n与纸的长边(单位:cm)和厚度x(单位:)满足.根据以上信息,当某张纸对折完4次时,的最小值为_________.现有一张长边为30 cm,厚度为0.01 cm的矩形纸,该矩形纸最多能对折_________次.(参考数值:)
【提升能力】
9.随着智能手机的普及,抖音、快手、火山视频等短视频APP迅速窜红.针对这种现状,某文化传媒有限公司决定逐年加大短视频制作的资金投入,若该公司2019年投入短视频制作的资金为5000万元人民币,在此基础上,若以后每年的资金投入均比上一年增长8%,则该公司投入短视频制作的资金开始超过6900万元人民币的年份是( ).(参考数据:,,)
A.2023年 B.2024年 C.2025年 D.2026年
10.已知定义域为R的偶函数满足,当时,,则方程在区间上所有解的和为( ).
A.8 B.7 C.6 D.5
11.(多选)已知函数有三个不同的零点,则实数a的取值可以为( )
A.0 B. C.3 D.4
12.(多选)已知定义域为R的偶函数有4个零点,,,,并且当时,,则下列说法中正确的是( )
A.实数a的取值范围是
B.当时,
C.
D.的取值范围是
13.已知函数,则函数的零点为________.
14.某种干细胞在培养过程中,每30分钟分裂一次(由一个分裂成两个),这种干细胞由1个培养成1024个需经过________小时.
【综合素养】
15.已知定义在R上的函数满足,且当时,,当时,,则函数在上有_________个零点.
16.“半斤不脸红,一斤不心跳,二斤倒不了!”酒驾者都有超乎寻常的“自信”,显然他们已经忘记了酒精会使人神经麻痹、迟钝的真理.世界卫生组织的事故调查显示,在中国,每年由于酒后驾车引发的交通事故达数万起,而造成死亡的事故中50%以上都与酒后驾车有关,酒后驾车的危害触目惊心,已经成为交通事故的第一大“杀手”.经过反复试验,一般情况下,某人喝一瓶红酒后酒精在人体血液中的变化规律的“散点图”如图所示,且该图表示的函数模型为.
(1)求a的值;
(2)当酒精含量大于20 mg/100mL是酒后驾车,则喝完一瓶红酒最少要经过多长时间才可以安全驾车?(时间以整小时计算)
答案以及解析
1.答案:B
解析:对于任意,函数满足,函数的图像关于点对称,函数的零点关于直线对称,函数的5个零点中有2对关于直线对称,中间的零点是2,.故选B.
2.答案:A
解析:设,则,,因为,所以是方程的实数根所在的一个区间.又在R上单调递增,故方程有唯一的实数根.故选A.
3.答案:C
解析:令,
当时,,
当时,,
即,又单调递增,其图象是连续不断的,所以的零点所在区间为,所以,故选C.
4.答案:C
解析:,,,在区间(1,1.5)内函数存在一个零点,该同学在第二次应计算的函数值为.故选C.
5.答案:D
解析:本题考查二分法求方程近似值的过程.设对区间至少二等分n次,此时区间长度为2,则第n次二等分后区间长为,依题意得,,,所以.
6.答案:A
解析:由题可得则解得,,所以,由函数解析式可知,在上单调递增,且,,故该果树的高度超过8m,至少需要4年.故选A.
7.答案:B
解析:假设至少需要经过的时间为x(单位:年),由题意得,两边同时取以为底的对数得,.
因为,所以,即.故选B.
8.答案:64,7
解析:由,得,郎,
,即的最小值为64.
由题意知,
故该矩形纸最多能对折7次.
9.答案:B
解析:当年份为n时,短视频制作的资金为(万元),,,由,两边同时取对数并整理得,
解得,从而得,
所以资金投入开始超过6900万元的年份是2024年.故选B.
10.答案:A
解析:因为满足,所以,所以的图象关于直线对称,
令,则的图象关于直线对称,作出函数与在上的图象,如图所示.
由图知与的图象在区间上共有8个交点,且两两关于直线对称,所以方程在区间上所有解的和为,故选A.
11.答案:CD
解析:当时,恒成立,即在区间上无零点,所以当时,有三个正根,解得或.当时,单调递增,且,则方程有一个根,则方程要有两个根,即有两个正数解,则,解得,故C、D项正确.
12.答案:BC
解析:对于A选项,因为为偶函数且有4个零点,所以当时有2个零点,故,故A错误;对于B选项,当时,,故,故B正确;对于C选项,由函数是偶函数,可知,且,,故,故C正确;对于D选项,,由,可知,函数在上单调递增,故,故D错误.故选BC.
13.答案:-8和2
解析:令,得.
当时,令,得;当时,,易知在区间上单调递增,又,所以.
故函数的零点为-8和2.
14.答案:5
解析:干细胞分裂一次时有2个细胞,分裂2次时变为个细胞,分裂n次时变为个细胞,,所以分裂10次,每小时分裂2次,所以需要5小时.
15.答案:7
解析:由知是奇函数,又当时,,所以在上是周期为1的周期函数.令得,结合当时,,作出函数和的大致图象,如图所示,数形结合可知函数和的图象在上有7个交点,即函数在上有7个零点.
16.(1)答案:
解析:当时,,解得.
(2)答案:最少经过6小时才可以驾车
解析:由题意得,即,从而,解得,
所以最少经过6小时才可以驾车.
2
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
