第一单元《长方体和正方体》(同步练习) 六年级上册数学苏教版(含答案)
文档属性
| 名称 | 第一单元《长方体和正方体》(同步练习) 六年级上册数学苏教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 43.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-05 20:39:22 | ||
图片预览




文档简介
23年秋学期苏教版数学六年级上册第一单元《长方体和正方体》课后练习五
学校:___________姓名:___________班级:___________
一、选择题
1.用一根铁丝刚好能围成一个长6cm、宽4cm、高2cm的长方体框架,现在要把这个长方体框架改成一个正方体框架,这个正方体框架的棱长最大是( )cm。
A.4 B.6 C.12 D.24
2.小明将一罐新买的饮料(净含量为650ml)完全浸没在一个装满水的盆中,盆中溢出( )的水。
A.正好650ml B.比650ml多 C.比650ml少 D.无法判断
3.一个正方体的棱长总和是60厘米,它的表面积是( )。
A.150平方厘米 B.125立方厘米 C.21600平方厘米 D.1.5平方米
4.若大正方体的体积是小正方体体积的8倍,则大正方体的表面积是小正方体的( )倍。
A.2 B.16 C.4 D.8
5.如图是一个物体的长、宽、高的数据,这个物体可能是( )。
A.六年级数学书 B.一本新华字典 C.普通橡皮 D.普通手机
二、填空题
6.700立方米=( )立方分米 ( )立方米=6升
4.082立方分米=( )毫升 900mL=( )L
7.把一个长8厘米、宽6厘米、高5厘米的长方体木块锯成两个同样大的小长方体,表面积至少增加( )平方厘米。
8.至少要( )个小正方体才能拼成一个大正方体,如果一个小正方体的棱长是1厘米,那么大正方体的表面积是( )平方厘米,体积是( )立方厘米。
9.把长10厘米、宽5厘米、厚3厘米的长方体肥皂2块包装在一起,最少用包装纸( )平方厘米。
10.一个棱长1分米的正方体锯成两个大小不同的长方体,大长方体的表面积比小长方体大200平方厘米,小长方体的表面积是( )平方厘米。
三、判断题
11.2.06升=206立方厘米。( )
12.表面积相等的长方体和正方体,它们的棱长总和一定相等。( )
13.正方体的棱长扩大2倍,它的体积就扩大8倍。( )
14.棱长是2cm的正方体,它的棱长总和与表面积大小相等。( )
15.两个表面积都是18平方厘米的小正方体,拼成一个长方体,长方体的表面积是36平方厘米。( )
四、图形计算
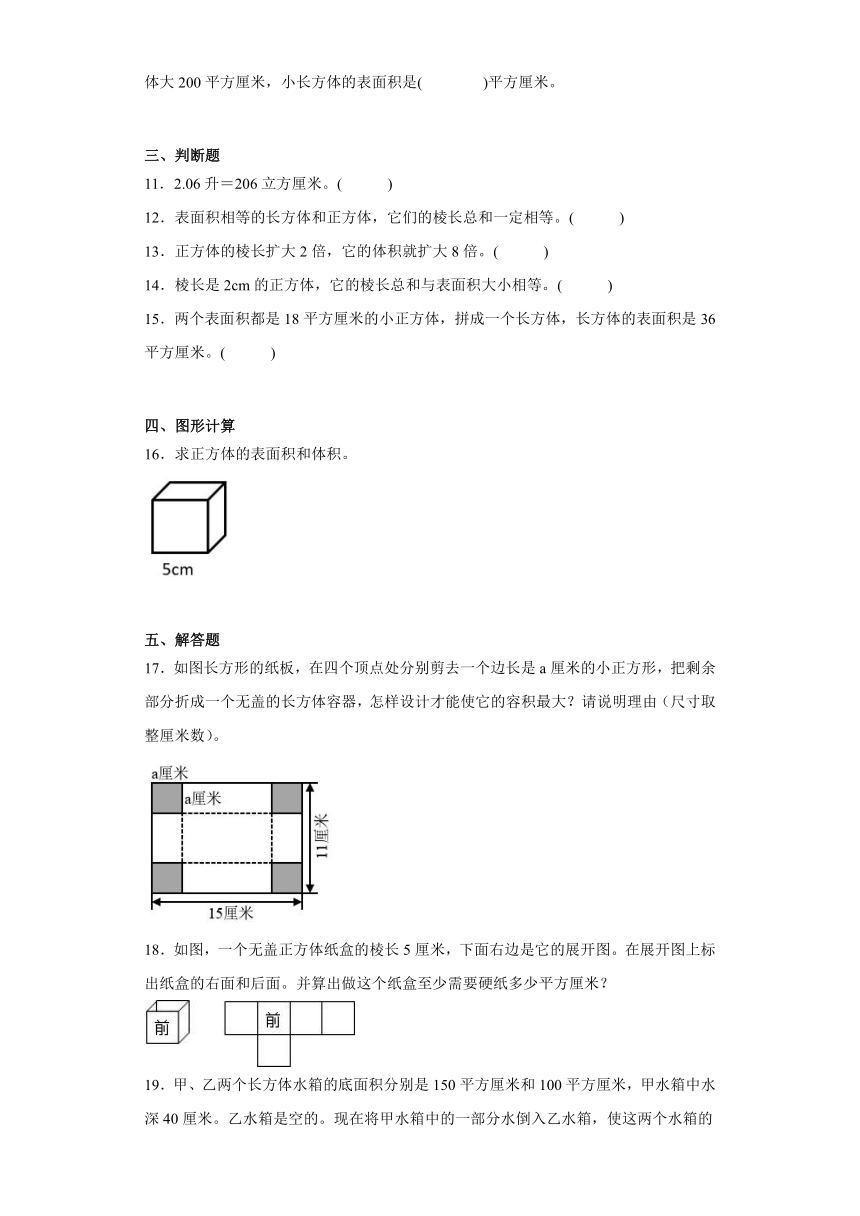
16.求正方体的表面积和体积。
五、解答题
17.如图长方形的纸板,在四个顶点处分别剪去一个边长是a厘米的小正方形,把剩余部分折成一个无盖的长方体容器,怎样设计才能使它的容积最大?请说明理由(尺寸取整厘米数)。
18.如图,一个无盖正方体纸盒的棱长5厘米,下面右边是它的展开图。在展开图上标出纸盒的右面和后面。并算出做这个纸盒至少需要硬纸多少平方厘米?
19.甲、乙两个长方体水箱的底面积分别是150平方厘米和100平方厘米,甲水箱中水深40厘米。乙水箱是空的。现在将甲水箱中的一部分水倒入乙水箱,使这两个水箱的水面高度相等。这时水面高是多少厘米?
参考答案:
1.A
【分析】由题意知:长方体的棱长总和等于正方体的棱长总和。根据长方体棱长总和=(长+宽+高)×4,可求得长方体的棱长总和,再用棱长总和除以12,即查正方体框架的棱长。据此解答。
【详解】(6+4+2)×4÷12
=12×4÷12
=48÷12
=4(cm)
这个正方体框架的棱长最大是4cm。
故答案为:A
【点睛】利用长方体棱长总和=(长+宽+高)×4,先求得长方体的棱长总和,再除以12是解答此题的关键。
2.B
【分析】根据题意可知,650 mL是这瓶饮料的净含量,所以饮料瓶的体积大于650 mL;然后根据盆里溢出的水等于饮料瓶的体积,可得盆里溢出的水比650mL多。
【详解】根据分析可知:
小明将一罐新买的饮料(净含量为650ml)完全浸没在一个装满水的盆中,盆中溢出比650ml多的水。
故答案为:B
【点睛】本题考查物体体积与容积的区别,物体的体积一般情况下大于它的容积。
3.A
【分析】根据正方体的棱长总和=棱长×12,据此求出正方体的棱长,再根据正方体的表面积公式:S=6a2,据此代入数值进行计算即可。
【详解】60÷12=5(厘米)
5×5×6
=25×6
=150(平方厘米)
则它的表面积是150平方厘米。
故答案为:A
【点睛】本题考查正方体的总棱长和表面积,熟记公式是解题的关键。
4.C
【分析】由题意可知,设小正方体的体积是1,则大正方体的体积是8,也就是说小正方体的棱长是1,大正方体的棱长是2,然后根据正方体的表面积公式:S=6a2,分别求出大、小两个正方体的表面积,最后用大正方体的表面积除以小正方体的表面积即可。
【详解】假设小正方体的体积是1,则大正方体的体积是8
(2×2×6)÷(1×1×6)
=24÷6
=4
则大正方体的表面积是小正方体的4倍。
故答案为:C
【点睛】本题考查正方体的体积和表面积,熟记公式是解题的关键。
5.A
【分析】这个物体长24cm,宽17cm,高0.7cm,新华字典的厚度比0.7cm大的多,普通橡皮和普通手机的长和宽比这个物体的长和宽小的多,这个物体很可能是数学书,据此解答。
【详解】分析可知,这个物体的长、宽、高接近六年级数学书的大小,所以这个物体可能是六年级数学书。
故答案为:A
【点睛】本题主要考查长方体的认识,联系生活实际用排除法找出正确的选项是解答题目的关键。
6. 700000 0.006 4082 0.9
【分析】1立方米=1000立方分米,大单位换小单位乘进率,即700×1000;
1立方米=1000升,小单位换大单位除以进率,即6÷1000;
1立方分米=1000毫升,大单位换小单位乘进率,即4.082×1000;
1L=1000mL,小单位换大单位除以进率,即900÷1000。
【详解】700立方米=700000立方分米
0.006立方米=6升
4.082立方分米=4082毫升
900mL=0.9L
【点睛】本题主要考查容积和体积单位之间的进率,熟练掌握它们的进率并灵活运用。
7.60
【分析】把一个长方体截成两个同样大小的小长方体,有3种不同的截法,要使表面积增加的最少,也就是把长方体的最小面平行截开,表面积增加两个截面的面积,根据长方形的面积公式:长×宽,把数据代入公式解答。
【详解】6×5×2
=30×2
=60(平方厘米)
即表面积至少增加60平方厘米。
【点睛】此题考查的目的是理解掌握长方体表面积的意义及应用,长方形面积公式及应用,关键是明确:要使表面积增加的最少,也就是把长方体的最小面平行截开。
8. 8 24 8
【分析】要用小正方体拼成一个大正方体,就要使沿着每条棱上摆的小正方体的个数相等, 即最少需要2×2×2=8个;根据正方体的表面积公式:棱长×棱长×6,体积公式:棱长×棱长×棱长即可求解。
【详解】2×2×2
=4×2
=8(个)
2×1=2(厘米)
2×2×6
=4×6
=24(平方厘米)
2×2×2
=4×2
=8(立方厘米)
即至少要8个小正方体才能拼成一个大正方体,如果一个小正方体的棱长是1厘米,那么大正方体的表面积是24平方厘米,体积是8立方厘米。
【点睛】此题考查了正方体的特征,以及正方体的表面积和体积公式。
9.280
【分析】将两个长方体拼在一起,想用最少的包装纸,即表面积最小,要将最大的面叠在一起,就会形成一个长10厘米、宽5厘米、厚3×2=6厘米的长方体,运用长方体的表面积公式:(长×宽+长×高+宽×高)×2,求出这个长方体的表面积即可。
【详解】3×2=6(厘米)
(10×5+10×6+5×6)×2
=(50+60+30)×2
=(110+30)×2
=140×2
=280(平方厘米)
即最少用包装纸280平方厘米。
【点睛】本题关键是要找出拼组后的长方体的长宽高各是多少,然后根据长方体表面积公式求解。
10.300
【分析】把正方体锯成两个大小不同的长方体,这两个长方体的表面积之和比正方体的表面积多2个面,即这两个长方体的表面积之和=棱长×棱长×(6+2),据此求出两个长方体的表面积之和;再根据大长方体的表面积比小长方体的表面积大200平方厘米,用两长方体的表面积之和减去200再除以2即可得到小长方体的表面积。
【详解】1分米=10厘米
10×10×(6+2)
=100×8
=800(平方厘米)
(800-200)÷2
=600÷2
=300(平方厘米)
小长方体的表面积是300平方厘米。
【点睛】掌握长方体的表面积计算公式是解答本题的关键。
11.×
【分析】根据1升=1立方分米,1立方分米=1000立方厘米,换算单位即可。
【详解】2.06升=2.06立方分米=2060立方厘米,原题说法错误。
故答案为:×
【点睛】此题考查了体积、容积单位间的换算,明确高级单位换算低级单位乘进率,低级单位换算高级单位除以进率。
12.×
【分析】长方体的表面积=(长×宽+长×高+宽×高)×2,棱长总和=(长+宽+高)×4;正方体的表面积=棱长×棱长×6,棱长总和=棱长×12。此题可以采用举例说明的方法进行判断。
【详解】假设长方体和正方体的表面积都是54平方厘米,则长方体的长、宽、高分别可能是6厘米、3厘米、1厘米,棱长总和=(6+3+1)×4=40(厘米);54=3×3×6,正方体的棱长是3厘米,棱长总和=3×12=36(厘米)。这个长方体和正方体表面积相等,但棱长总和不相等。
故答案为:×
【点睛】此题主要考查正方体、长方体的表面积和棱长总和公式的灵活应用,这类问题可以举例子说明。
13.√
【分析】正方体的体积=棱长×棱长×棱长,再根据因数与积的变化规律,积扩大的倍数等于因数扩大倍数的乘积,据此判断。
【详解】正方体的棱长扩大2倍,正方体的体积扩大2×2×2=8倍。
故答案为:√
【点睛】此题主要考查正方体的体积公式的灵活运用,以及因数与积的变化规律的应用。
14.×
【分析】正方体共有12条棱,可求出总的棱长;正方体的表面积公式为棱长×棱长×6,可求出表面积,再对二者进行比较,需要注意单位的不同,即可解出本题。
【详解】正方体的棱长总和为:(cm);
正方体的表面积为:(cm2),二者虽然数字一样,但一个表示的是长度,另一个表示面积,度量单位不同,无法比较,故本题错误。
【点睛】本题主要考查的是正方体的棱长和表面积计算,需要注意的是两者单位并不同,是不同度量单位,无法直接比较。
15.×
【分析】两个正方体拼成一个长方体,有两个面挨在一起了,长方体的表面积需要减去小正方形体的两个挨在一起表面的面积,即可解答。
【详解】18×2-(18÷6)×2
=36-3×2
=36-6
=30(平方厘米)
两个表面积都是18平方厘米的小正方体,拼成一个长方体,长方体表面积是30平方厘米,拼成长方体的表面积是36平方厘米是错的。
故答案为:×
【点睛】本题考查小正方体拼成长方体后的表面积的变化,关键是拼成长方体后的表面积减少了。
16.表面积:150cm2;体积:125cm3
【分析】根据正方体表面积公式:表面积=棱长×棱长×6,正方体体积公式:体积=棱长×棱长×棱长,代入数据,即可解答。
【详解】表面积:5×5×6
=25×6
=150(cm2)
体积:5×5×5
=25×5
=125(cm3)
17.a=2厘米时,长方体容积最大;理由见详解
【分析】因为长、宽、高都是整厘米数,且四个角剪去的小正方形均相同,小正方形的边长就是这个长方体盒子的高,根据长方体体积公式:体积=长×宽×高;分别求出当a是1厘米、2厘米、3厘米……,求出长方体的容积,再进行比较,即可解答。
【详解】当a=1厘米时,这个长方体的长是15-1-1=13(厘米),宽是11-1-1=9(厘米),高是1厘米;容积是:
13×9×1
=117×1
=117(立方厘米)
当a=2厘米时,这个长方体的长是15-2-2=11(厘米),宽是11-2-2=7(厘米),高是2厘米;容积是:
11×7×2
=77×2
=154(立方厘米)
当a=3厘米时,这个长方体的长是15-3-3=9(厘米),宽是11-3-3=5(厘米),高是3厘米;容积是:
9×5×3
=45×3
=135(立方厘米)
当a=4厘米时,这个长方体的长是15-4-4=7(厘米),宽是11-4-4=3(厘米),高是4厘米;容积是:
7×3×4
=21×4
=84(立方厘米)
当a=5厘米时,这个长方体的长是15-5-5=5(厘米),宽是11-5-5=1(厘米),高是5厘米;容积是:
5×1×5
=5×5
=25(立方厘米)
154>135>117>84>25
当a=2厘米,长方体的容积最大。
答:当剪去一个边长是2厘米的小正方形时,这个无盖的长方体容器最大。
【点睛】解答本题的关键是熟练掌握长方体体积公式,理由长方体体积公式进行解答。
18.图见详解;125平方厘米
【分析】由图可知,与前相隔一格的是它的相对面,也就是后面,展开图前的下面一格是下面,前面左面一格是左面,右面一格是右面,据此标出;需要硬纸的面积也就是正方体5个面的面积之和,据此解答。
【详解】作图如下:
5×5×5
=25×5
=125(平方厘米)
答:做这个纸盒至少需要硬纸125平方厘米。
【点睛】此题考查了正方体的展开图以及表面积的相关计算,需要有一定的空间想象能力。
19.24厘米
【分析】根据长方体体积公式:体积=底面积×高,代入数据,求出甲水箱水的体积;甲、乙两个水箱的体积和等于原来甲水箱的体积,高=体积÷底面积;用甲水箱原来的体积除以甲、乙两水箱的底面积和,即可求出这时水面的高度,据此解答。
【详解】150×40÷(150+100)
=6000÷250
=24(厘米)
答:这时水面高是24厘米。
【点睛】解答本题的关键明确两个水箱的水面高度相同,两个水箱的体积和等于原来甲水箱的体积。
学校:___________姓名:___________班级:___________
一、选择题
1.用一根铁丝刚好能围成一个长6cm、宽4cm、高2cm的长方体框架,现在要把这个长方体框架改成一个正方体框架,这个正方体框架的棱长最大是( )cm。
A.4 B.6 C.12 D.24
2.小明将一罐新买的饮料(净含量为650ml)完全浸没在一个装满水的盆中,盆中溢出( )的水。
A.正好650ml B.比650ml多 C.比650ml少 D.无法判断
3.一个正方体的棱长总和是60厘米,它的表面积是( )。
A.150平方厘米 B.125立方厘米 C.21600平方厘米 D.1.5平方米
4.若大正方体的体积是小正方体体积的8倍,则大正方体的表面积是小正方体的( )倍。
A.2 B.16 C.4 D.8
5.如图是一个物体的长、宽、高的数据,这个物体可能是( )。
A.六年级数学书 B.一本新华字典 C.普通橡皮 D.普通手机
二、填空题
6.700立方米=( )立方分米 ( )立方米=6升
4.082立方分米=( )毫升 900mL=( )L
7.把一个长8厘米、宽6厘米、高5厘米的长方体木块锯成两个同样大的小长方体,表面积至少增加( )平方厘米。
8.至少要( )个小正方体才能拼成一个大正方体,如果一个小正方体的棱长是1厘米,那么大正方体的表面积是( )平方厘米,体积是( )立方厘米。
9.把长10厘米、宽5厘米、厚3厘米的长方体肥皂2块包装在一起,最少用包装纸( )平方厘米。
10.一个棱长1分米的正方体锯成两个大小不同的长方体,大长方体的表面积比小长方体大200平方厘米,小长方体的表面积是( )平方厘米。
三、判断题
11.2.06升=206立方厘米。( )
12.表面积相等的长方体和正方体,它们的棱长总和一定相等。( )
13.正方体的棱长扩大2倍,它的体积就扩大8倍。( )
14.棱长是2cm的正方体,它的棱长总和与表面积大小相等。( )
15.两个表面积都是18平方厘米的小正方体,拼成一个长方体,长方体的表面积是36平方厘米。( )
四、图形计算
16.求正方体的表面积和体积。
五、解答题
17.如图长方形的纸板,在四个顶点处分别剪去一个边长是a厘米的小正方形,把剩余部分折成一个无盖的长方体容器,怎样设计才能使它的容积最大?请说明理由(尺寸取整厘米数)。
18.如图,一个无盖正方体纸盒的棱长5厘米,下面右边是它的展开图。在展开图上标出纸盒的右面和后面。并算出做这个纸盒至少需要硬纸多少平方厘米?
19.甲、乙两个长方体水箱的底面积分别是150平方厘米和100平方厘米,甲水箱中水深40厘米。乙水箱是空的。现在将甲水箱中的一部分水倒入乙水箱,使这两个水箱的水面高度相等。这时水面高是多少厘米?
参考答案:
1.A
【分析】由题意知:长方体的棱长总和等于正方体的棱长总和。根据长方体棱长总和=(长+宽+高)×4,可求得长方体的棱长总和,再用棱长总和除以12,即查正方体框架的棱长。据此解答。
【详解】(6+4+2)×4÷12
=12×4÷12
=48÷12
=4(cm)
这个正方体框架的棱长最大是4cm。
故答案为:A
【点睛】利用长方体棱长总和=(长+宽+高)×4,先求得长方体的棱长总和,再除以12是解答此题的关键。
2.B
【分析】根据题意可知,650 mL是这瓶饮料的净含量,所以饮料瓶的体积大于650 mL;然后根据盆里溢出的水等于饮料瓶的体积,可得盆里溢出的水比650mL多。
【详解】根据分析可知:
小明将一罐新买的饮料(净含量为650ml)完全浸没在一个装满水的盆中,盆中溢出比650ml多的水。
故答案为:B
【点睛】本题考查物体体积与容积的区别,物体的体积一般情况下大于它的容积。
3.A
【分析】根据正方体的棱长总和=棱长×12,据此求出正方体的棱长,再根据正方体的表面积公式:S=6a2,据此代入数值进行计算即可。
【详解】60÷12=5(厘米)
5×5×6
=25×6
=150(平方厘米)
则它的表面积是150平方厘米。
故答案为:A
【点睛】本题考查正方体的总棱长和表面积,熟记公式是解题的关键。
4.C
【分析】由题意可知,设小正方体的体积是1,则大正方体的体积是8,也就是说小正方体的棱长是1,大正方体的棱长是2,然后根据正方体的表面积公式:S=6a2,分别求出大、小两个正方体的表面积,最后用大正方体的表面积除以小正方体的表面积即可。
【详解】假设小正方体的体积是1,则大正方体的体积是8
(2×2×6)÷(1×1×6)
=24÷6
=4
则大正方体的表面积是小正方体的4倍。
故答案为:C
【点睛】本题考查正方体的体积和表面积,熟记公式是解题的关键。
5.A
【分析】这个物体长24cm,宽17cm,高0.7cm,新华字典的厚度比0.7cm大的多,普通橡皮和普通手机的长和宽比这个物体的长和宽小的多,这个物体很可能是数学书,据此解答。
【详解】分析可知,这个物体的长、宽、高接近六年级数学书的大小,所以这个物体可能是六年级数学书。
故答案为:A
【点睛】本题主要考查长方体的认识,联系生活实际用排除法找出正确的选项是解答题目的关键。
6. 700000 0.006 4082 0.9
【分析】1立方米=1000立方分米,大单位换小单位乘进率,即700×1000;
1立方米=1000升,小单位换大单位除以进率,即6÷1000;
1立方分米=1000毫升,大单位换小单位乘进率,即4.082×1000;
1L=1000mL,小单位换大单位除以进率,即900÷1000。
【详解】700立方米=700000立方分米
0.006立方米=6升
4.082立方分米=4082毫升
900mL=0.9L
【点睛】本题主要考查容积和体积单位之间的进率,熟练掌握它们的进率并灵活运用。
7.60
【分析】把一个长方体截成两个同样大小的小长方体,有3种不同的截法,要使表面积增加的最少,也就是把长方体的最小面平行截开,表面积增加两个截面的面积,根据长方形的面积公式:长×宽,把数据代入公式解答。
【详解】6×5×2
=30×2
=60(平方厘米)
即表面积至少增加60平方厘米。
【点睛】此题考查的目的是理解掌握长方体表面积的意义及应用,长方形面积公式及应用,关键是明确:要使表面积增加的最少,也就是把长方体的最小面平行截开。
8. 8 24 8
【分析】要用小正方体拼成一个大正方体,就要使沿着每条棱上摆的小正方体的个数相等, 即最少需要2×2×2=8个;根据正方体的表面积公式:棱长×棱长×6,体积公式:棱长×棱长×棱长即可求解。
【详解】2×2×2
=4×2
=8(个)
2×1=2(厘米)
2×2×6
=4×6
=24(平方厘米)
2×2×2
=4×2
=8(立方厘米)
即至少要8个小正方体才能拼成一个大正方体,如果一个小正方体的棱长是1厘米,那么大正方体的表面积是24平方厘米,体积是8立方厘米。
【点睛】此题考查了正方体的特征,以及正方体的表面积和体积公式。
9.280
【分析】将两个长方体拼在一起,想用最少的包装纸,即表面积最小,要将最大的面叠在一起,就会形成一个长10厘米、宽5厘米、厚3×2=6厘米的长方体,运用长方体的表面积公式:(长×宽+长×高+宽×高)×2,求出这个长方体的表面积即可。
【详解】3×2=6(厘米)
(10×5+10×6+5×6)×2
=(50+60+30)×2
=(110+30)×2
=140×2
=280(平方厘米)
即最少用包装纸280平方厘米。
【点睛】本题关键是要找出拼组后的长方体的长宽高各是多少,然后根据长方体表面积公式求解。
10.300
【分析】把正方体锯成两个大小不同的长方体,这两个长方体的表面积之和比正方体的表面积多2个面,即这两个长方体的表面积之和=棱长×棱长×(6+2),据此求出两个长方体的表面积之和;再根据大长方体的表面积比小长方体的表面积大200平方厘米,用两长方体的表面积之和减去200再除以2即可得到小长方体的表面积。
【详解】1分米=10厘米
10×10×(6+2)
=100×8
=800(平方厘米)
(800-200)÷2
=600÷2
=300(平方厘米)
小长方体的表面积是300平方厘米。
【点睛】掌握长方体的表面积计算公式是解答本题的关键。
11.×
【分析】根据1升=1立方分米,1立方分米=1000立方厘米,换算单位即可。
【详解】2.06升=2.06立方分米=2060立方厘米,原题说法错误。
故答案为:×
【点睛】此题考查了体积、容积单位间的换算,明确高级单位换算低级单位乘进率,低级单位换算高级单位除以进率。
12.×
【分析】长方体的表面积=(长×宽+长×高+宽×高)×2,棱长总和=(长+宽+高)×4;正方体的表面积=棱长×棱长×6,棱长总和=棱长×12。此题可以采用举例说明的方法进行判断。
【详解】假设长方体和正方体的表面积都是54平方厘米,则长方体的长、宽、高分别可能是6厘米、3厘米、1厘米,棱长总和=(6+3+1)×4=40(厘米);54=3×3×6,正方体的棱长是3厘米,棱长总和=3×12=36(厘米)。这个长方体和正方体表面积相等,但棱长总和不相等。
故答案为:×
【点睛】此题主要考查正方体、长方体的表面积和棱长总和公式的灵活应用,这类问题可以举例子说明。
13.√
【分析】正方体的体积=棱长×棱长×棱长,再根据因数与积的变化规律,积扩大的倍数等于因数扩大倍数的乘积,据此判断。
【详解】正方体的棱长扩大2倍,正方体的体积扩大2×2×2=8倍。
故答案为:√
【点睛】此题主要考查正方体的体积公式的灵活运用,以及因数与积的变化规律的应用。
14.×
【分析】正方体共有12条棱,可求出总的棱长;正方体的表面积公式为棱长×棱长×6,可求出表面积,再对二者进行比较,需要注意单位的不同,即可解出本题。
【详解】正方体的棱长总和为:(cm);
正方体的表面积为:(cm2),二者虽然数字一样,但一个表示的是长度,另一个表示面积,度量单位不同,无法比较,故本题错误。
【点睛】本题主要考查的是正方体的棱长和表面积计算,需要注意的是两者单位并不同,是不同度量单位,无法直接比较。
15.×
【分析】两个正方体拼成一个长方体,有两个面挨在一起了,长方体的表面积需要减去小正方形体的两个挨在一起表面的面积,即可解答。
【详解】18×2-(18÷6)×2
=36-3×2
=36-6
=30(平方厘米)
两个表面积都是18平方厘米的小正方体,拼成一个长方体,长方体表面积是30平方厘米,拼成长方体的表面积是36平方厘米是错的。
故答案为:×
【点睛】本题考查小正方体拼成长方体后的表面积的变化,关键是拼成长方体后的表面积减少了。
16.表面积:150cm2;体积:125cm3
【分析】根据正方体表面积公式:表面积=棱长×棱长×6,正方体体积公式:体积=棱长×棱长×棱长,代入数据,即可解答。
【详解】表面积:5×5×6
=25×6
=150(cm2)
体积:5×5×5
=25×5
=125(cm3)
17.a=2厘米时,长方体容积最大;理由见详解
【分析】因为长、宽、高都是整厘米数,且四个角剪去的小正方形均相同,小正方形的边长就是这个长方体盒子的高,根据长方体体积公式:体积=长×宽×高;分别求出当a是1厘米、2厘米、3厘米……,求出长方体的容积,再进行比较,即可解答。
【详解】当a=1厘米时,这个长方体的长是15-1-1=13(厘米),宽是11-1-1=9(厘米),高是1厘米;容积是:
13×9×1
=117×1
=117(立方厘米)
当a=2厘米时,这个长方体的长是15-2-2=11(厘米),宽是11-2-2=7(厘米),高是2厘米;容积是:
11×7×2
=77×2
=154(立方厘米)
当a=3厘米时,这个长方体的长是15-3-3=9(厘米),宽是11-3-3=5(厘米),高是3厘米;容积是:
9×5×3
=45×3
=135(立方厘米)
当a=4厘米时,这个长方体的长是15-4-4=7(厘米),宽是11-4-4=3(厘米),高是4厘米;容积是:
7×3×4
=21×4
=84(立方厘米)
当a=5厘米时,这个长方体的长是15-5-5=5(厘米),宽是11-5-5=1(厘米),高是5厘米;容积是:
5×1×5
=5×5
=25(立方厘米)
154>135>117>84>25
当a=2厘米,长方体的容积最大。
答:当剪去一个边长是2厘米的小正方形时,这个无盖的长方体容器最大。
【点睛】解答本题的关键是熟练掌握长方体体积公式,理由长方体体积公式进行解答。
18.图见详解;125平方厘米
【分析】由图可知,与前相隔一格的是它的相对面,也就是后面,展开图前的下面一格是下面,前面左面一格是左面,右面一格是右面,据此标出;需要硬纸的面积也就是正方体5个面的面积之和,据此解答。
【详解】作图如下:
5×5×5
=25×5
=125(平方厘米)
答:做这个纸盒至少需要硬纸125平方厘米。
【点睛】此题考查了正方体的展开图以及表面积的相关计算,需要有一定的空间想象能力。
19.24厘米
【分析】根据长方体体积公式:体积=底面积×高,代入数据,求出甲水箱水的体积;甲、乙两个水箱的体积和等于原来甲水箱的体积,高=体积÷底面积;用甲水箱原来的体积除以甲、乙两水箱的底面积和,即可求出这时水面的高度,据此解答。
【详解】150×40÷(150+100)
=6000÷250
=24(厘米)
答:这时水面高是24厘米。
【点睛】解答本题的关键明确两个水箱的水面高度相同,两个水箱的体积和等于原来甲水箱的体积。
