4.长方体和正方体的表面积(2)(课件)六年级上册数学苏教版(共21张PPT)
文档属性
| 名称 | 4.长方体和正方体的表面积(2)(课件)六年级上册数学苏教版(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-06 19:38:58 | ||
图片预览






文档简介
(共21张PPT)
长方体和正方体
表面积(2)
学习目标
1.进一步理解长方体和正方体表面积的意义。
2.进一步熟悉长方体和正方体表面积的计算方法,会解决一些生活中的实际问题。
教学重点:
用长方体和正方体的表面积公式解决实际问题。
教学难点:
如何将实际问题转化为数学问题。
复习:
2.长方体有( )个面,一般是( )形,( )面的面积相等。长方形
上下每个面的面积=( )×( ),
左右每个面的面积=( )×( ),
前后每个面的面积=( )×( )。
1.长方体或正方体( )叫做它们的表面积。
六个面的总面积
6
长方
相对
长
宽
宽
高
长
高
长方体的表面积=长×宽×2+长×高×2+宽×高×2
长方体的表面积=(长×宽+长×高+宽×高)×2
3. 正方体有( )个面, 都是( )形,( )面 的面积相等。
正方体每个面的面积=( )×( ),
6
正方
所有
棱长
棱长
正方体的表面积=棱长×棱长×6
5
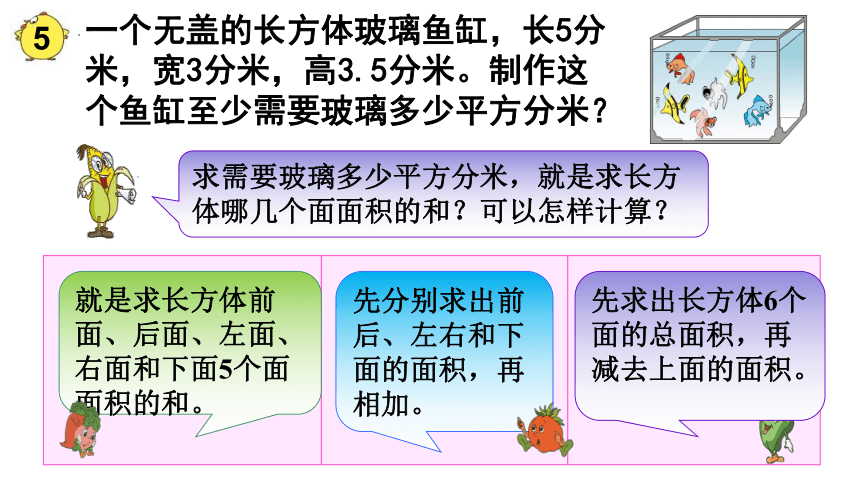
一个无盖的长方体玻璃鱼缸,长5分米,宽3分米,高3.5分米。制作这个鱼缸至少需要玻璃多少平方分米?
求需要玻璃多少平方分米,就是求长方体哪几个面面积的和?可以怎样计算?
就是求长方体前面、后面、左面、右面和下面5个面面积的和。
先分别求出前后、左右和下面的面积,再相加。
先求出长方体6个面的总面积,再减去上面的面积。
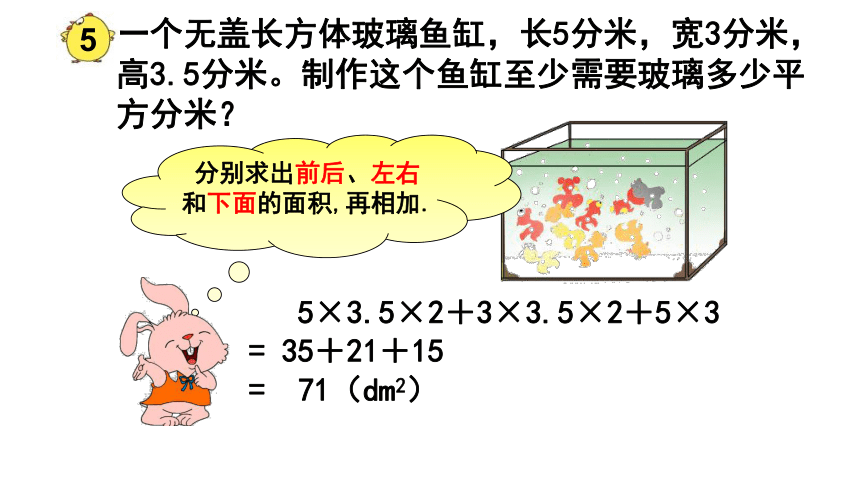
一个无盖长方体玻璃鱼缸,长5分米,宽3分米,高3.5分米。制作这个鱼缸至少需要玻璃多少平方分米?
分别求出前后、左右和下面的面积,再相加.
5×3.5×2+3×3.5×2+5×3
= 35+21+15
= 71(dm2)
5
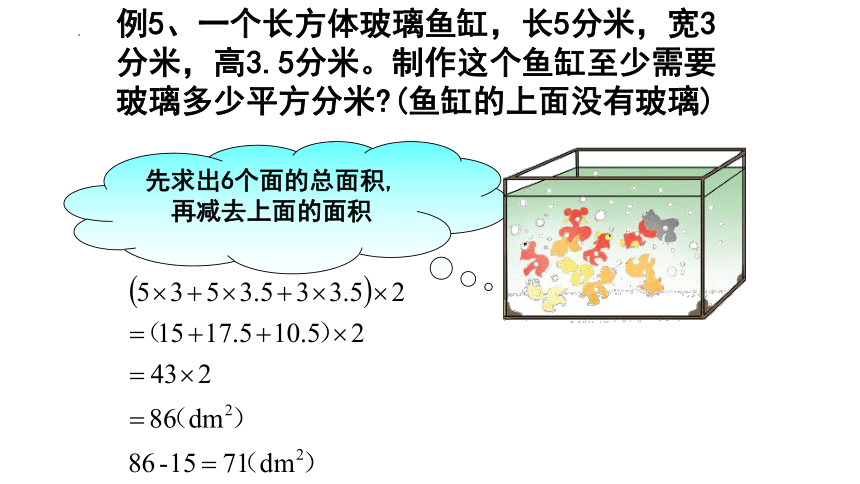
先求出6个面的总面积,再减去上面的面积
例5、一个长方体玻璃鱼缸,长5分米,宽3分米,高3.5分米。制作这个鱼缸至少需要玻璃多少平方分米 (鱼缸的上面没有玻璃)
思考:用计算长方体表面积的方法解决实际问题时,要注意什么?
要根据实际问题,确定计算哪几个面面积的和。
可以根据长方体面的特征,用不同的方法计算。
14cm
10cm
8cm
10cm
10cm
10cm
赵小明做了两个无盖的纸盒(如下图),至少各用多少平方厘米纸板?
做一个流水槽(如下图),长1米,宽2分米,高1分米。做这个水槽至少要多少平方分米的铁皮?
前后+下
6.一个长方体饼干盒,长8厘米,宽5厘米,高10厘米。如果在它的四周贴上商标纸(如下图),至少要用多少平方厘米纸板?
求商标纸至少用多少平方厘米就是求就是求长方体哪几个面面积的和?
前后+左右
8×10×2+5×10×2=260(平方厘米)
6.一个长方体饼干盒,长8厘米,宽5厘米,高10厘米。如果在它的四周贴上商标纸(如下图),至少要用多少平方厘米纸板?
饼干
(8+5)×2×10=260(平方厘米)
长方体前、后、左、右4个面的总面积是长方体的侧面积。
长方体的侧面积=前后面积+左右面积
长方体的侧面积=底面周长×高
在实际生活中,经常遇到不需要计算长方体或正方体六个面总面积的情况。因此,要根据具体问题具体分析,要搞清计算的是哪几个面的面积,再进而确定计算表面积的方法,不能生搬硬套计算公式。
总 结
(1)长方体通风管道的用料面积
(2)长方体水池内铺瓷砖的面积
(3)教室内粉刷墙面的面积
(4)长方体油桶的用料面积
这些问题分别要求长方体哪几个面的面积?
考考你的想象力:
教学小结
通过今天的学习,你有什么收获?
在解决这些问题时,你有什么需要提醒大
家注意的?
7.一个用硬纸板做成的长方体影集封套长31厘米,宽27厘米,高2.5厘米。封套的左面不封口。(如右图),做这个封套至少需要多少平方厘米硬纸板
前后+上下+右
27
如果每平方米需要白色涂料4千克,一共要白色涂料多少千克?
如果每千克白色涂料可粉刷4平方米,一共要白色涂料多少千克?
8
4
5
20
4cm
3cm
1cm
长方体和正方体
表面积(2)
学习目标
1.进一步理解长方体和正方体表面积的意义。
2.进一步熟悉长方体和正方体表面积的计算方法,会解决一些生活中的实际问题。
教学重点:
用长方体和正方体的表面积公式解决实际问题。
教学难点:
如何将实际问题转化为数学问题。
复习:
2.长方体有( )个面,一般是( )形,( )面的面积相等。长方形
上下每个面的面积=( )×( ),
左右每个面的面积=( )×( ),
前后每个面的面积=( )×( )。
1.长方体或正方体( )叫做它们的表面积。
六个面的总面积
6
长方
相对
长
宽
宽
高
长
高
长方体的表面积=长×宽×2+长×高×2+宽×高×2
长方体的表面积=(长×宽+长×高+宽×高)×2
3. 正方体有( )个面, 都是( )形,( )面 的面积相等。
正方体每个面的面积=( )×( ),
6
正方
所有
棱长
棱长
正方体的表面积=棱长×棱长×6
5
一个无盖的长方体玻璃鱼缸,长5分米,宽3分米,高3.5分米。制作这个鱼缸至少需要玻璃多少平方分米?
求需要玻璃多少平方分米,就是求长方体哪几个面面积的和?可以怎样计算?
就是求长方体前面、后面、左面、右面和下面5个面面积的和。
先分别求出前后、左右和下面的面积,再相加。
先求出长方体6个面的总面积,再减去上面的面积。
一个无盖长方体玻璃鱼缸,长5分米,宽3分米,高3.5分米。制作这个鱼缸至少需要玻璃多少平方分米?
分别求出前后、左右和下面的面积,再相加.
5×3.5×2+3×3.5×2+5×3
= 35+21+15
= 71(dm2)
5
先求出6个面的总面积,再减去上面的面积
例5、一个长方体玻璃鱼缸,长5分米,宽3分米,高3.5分米。制作这个鱼缸至少需要玻璃多少平方分米 (鱼缸的上面没有玻璃)
思考:用计算长方体表面积的方法解决实际问题时,要注意什么?
要根据实际问题,确定计算哪几个面面积的和。
可以根据长方体面的特征,用不同的方法计算。
14cm
10cm
8cm
10cm
10cm
10cm
赵小明做了两个无盖的纸盒(如下图),至少各用多少平方厘米纸板?
做一个流水槽(如下图),长1米,宽2分米,高1分米。做这个水槽至少要多少平方分米的铁皮?
前后+下
6.一个长方体饼干盒,长8厘米,宽5厘米,高10厘米。如果在它的四周贴上商标纸(如下图),至少要用多少平方厘米纸板?
求商标纸至少用多少平方厘米就是求就是求长方体哪几个面面积的和?
前后+左右
8×10×2+5×10×2=260(平方厘米)
6.一个长方体饼干盒,长8厘米,宽5厘米,高10厘米。如果在它的四周贴上商标纸(如下图),至少要用多少平方厘米纸板?
饼干
(8+5)×2×10=260(平方厘米)
长方体前、后、左、右4个面的总面积是长方体的侧面积。
长方体的侧面积=前后面积+左右面积
长方体的侧面积=底面周长×高
在实际生活中,经常遇到不需要计算长方体或正方体六个面总面积的情况。因此,要根据具体问题具体分析,要搞清计算的是哪几个面的面积,再进而确定计算表面积的方法,不能生搬硬套计算公式。
总 结
(1)长方体通风管道的用料面积
(2)长方体水池内铺瓷砖的面积
(3)教室内粉刷墙面的面积
(4)长方体油桶的用料面积
这些问题分别要求长方体哪几个面的面积?
考考你的想象力:
教学小结
通过今天的学习,你有什么收获?
在解决这些问题时,你有什么需要提醒大
家注意的?
7.一个用硬纸板做成的长方体影集封套长31厘米,宽27厘米,高2.5厘米。封套的左面不封口。(如右图),做这个封套至少需要多少平方厘米硬纸板
前后+上下+右
27
如果每平方米需要白色涂料4千克,一共要白色涂料多少千克?
如果每千克白色涂料可粉刷4平方米,一共要白色涂料多少千克?
8
4
5
20
4cm
3cm
1cm
