第四单元《比》(单元复习课件)六年级数学上册 人教版(18页PPT)
文档属性
| 名称 | 第四单元《比》(单元复习课件)六年级数学上册 人教版(18页PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 629.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-06 20:33:16 | ||
图片预览


文档简介
第4单元 比
人教版·六年级上册
单元知识体系梳理
1
重难点易错点剖析
2
变式巩固练习
3
综合拓展延伸
4
Text here
单元知识体系框架梳理
比
比的各部分名称
比的意义
比的基本性质
比、除法、分数的关系
份数法
化简比
分数法
比的意义
比的基本性质
按比分配问题
Text here
重难易错点剖析
Text here
重难易错点剖析
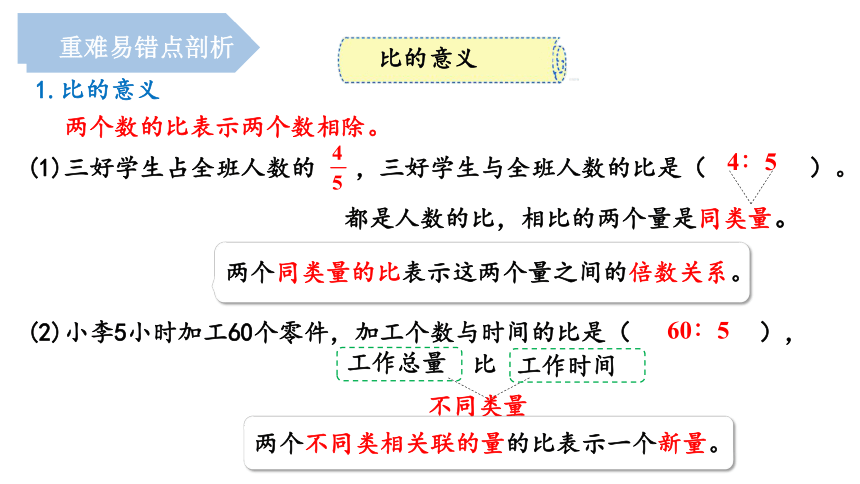
1.比的意义
比的意义
(1)三好学生占全班人数的 ,三好学生与全班人数的比是( )。
(2)小李5小时加工60个零件,加工个数与时间的比是( ),
4∶5
60∶5
都是人数的比,相比的两个量是同类量。
两个同类量的比表示这两个量之间的倍数关系。
工作总量
工作时间
比
不同类量
两个不同类相关联的量的比表示一个新量。
两个数的比表示两个数相除。
Text here
重难易错点剖析
Text here
重难易错点剖析
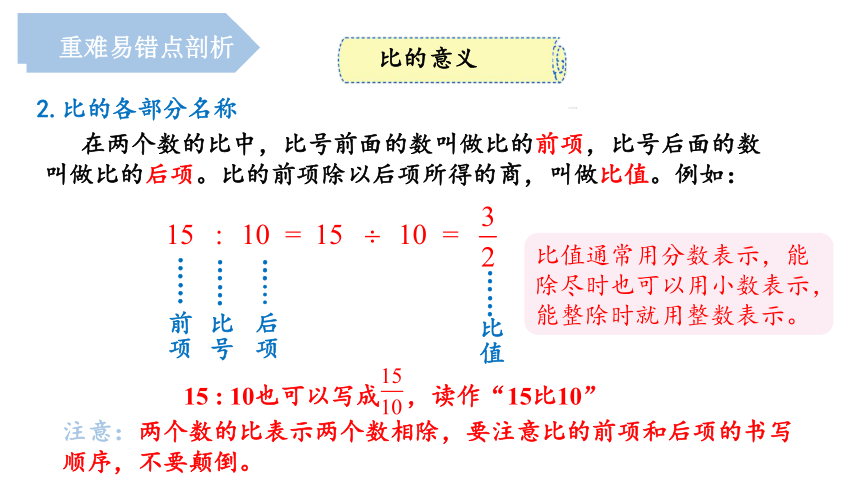
2.比的各部分名称
比的意义
前项
后项
比号
比值
……
……
……
……
比值通常用分数表示,能除尽时也可以用小数表示,能整除时就用整数表示。
在两个数的比中,比号前面的数叫做比的前项,比号后面的数叫做比的后项。比的前项除以后项所得的商,叫做比值。例如:
15 : 10也可以写成 ,读作“15比10”
注意:两个数的比表示两个数相除,要注意比的前项和后项的书写顺序,不要颠倒。
Text here
重难易错点剖析
Text here
重难易错点剖析
比的意义
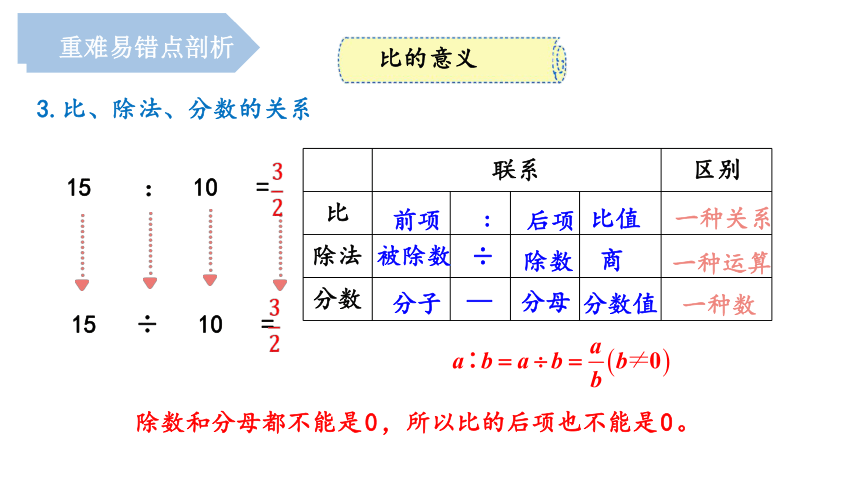
3.比、除法、分数的关系
15 : 10 =
15 ÷ 10 =
除数和分母都不能是0,所以比的后项也不能是0。
????????
?
????????
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
联系
区别
比
除法
分数
分子
—
分母
分数值
一种数
被除数
÷
除数
商
一种运算
前项
:
后项
比值
一种关系
Text here
重难易错点剖析
比的基本性质
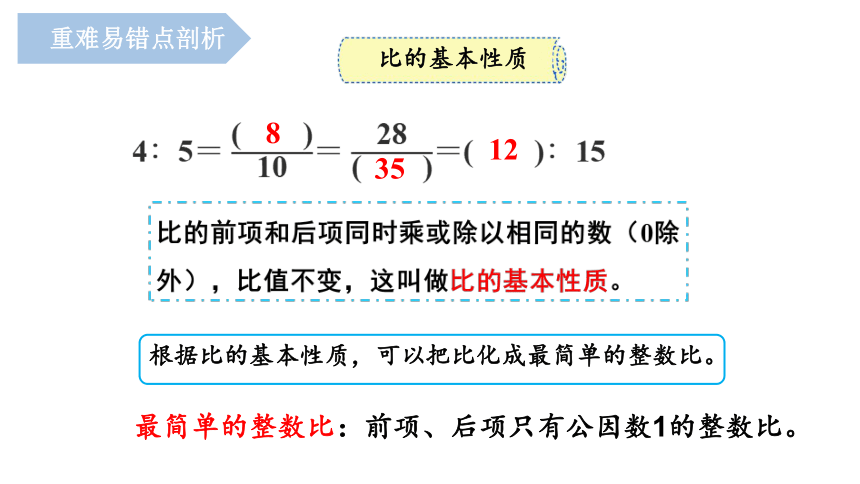
4∶5= ( )????????= ????????( )=( )∶15
?
8
35
12
根据比的基本性质,可以把比化成最简单的整数比。
最简单的整数比:前项、后项只有公因数1的整数比。
Text here
重难易错点剖析
比的基本性质
????????∶???????????? ????????∶????????
=(???????? × )∶(???????????? × ) = (????????)(????????) × (????????)(????????)
=( )∶( ) =( )∶( )
?
24
24
9
10
5
9
6
5
2
3
4.化简分数比:
方法一:比的前项、后项同时乘它们分母的最小公倍数 →整数比→最简单的整数比。
方法二:比的前项除以后项,求出比值→化成最简分数→最简单的整数比。
Text here
重难易错点剖析
32∶40
=(32÷8)∶(40÷8)
=4∶5
5.化简整数比。
比的基本性质
比的前项、后项同时除以它们的最大公因数。
最简单整数比
Text here
重难易错点剖析
=(3.2×100)∶(0.16×100)
=(320÷16)∶(16÷16)
=20∶1
比的基本性质
3.2∶0.16
6.化简小数比。
比的前项、后项同时扩大相同的倍数。
整数比
最简单整数比
Text here
重难易错点剖析
按比分配问题
六(1)班分成两组打扫卫生,室外组有30人,室内组有20人,把40个清扫工具按照两个组的人数比分配给各组,室外组、室内组各分到多少个清扫工具?
室外组与室内组的人数比为30:20=3:2
8×3=24(个)
8×2=16(个)
40÷(3+2)=8(个)
答:室外组分到24个清扫工具,室内组分到16个清扫工具。
1.份数法
方法:把比看作分得的份数之比,先求出总份数,然后求出每份的数量,再求出各部分对应的具体数量。
总数量÷总份数=每份的数量
每份的数量×各部分对应的份数=各部分的数量
Text here
重难易错点剖析
按比分配问题
六(1)班分成两组打扫卫生,室外组有30人,室内组有20人,把40个清扫工具按照两个组的人数比分配给各组,室外组、室内组各分到多少个清扫工具?
2.分数法
室外组与室内组的人数比为30:20=3:2
答:室外组分到24个清扫工具,室内组分到16个清扫工具。
=24(个)
3+2
3
40×
40×
3+2
2
=16(个)
方法:把比转化为分数,先求出各部分的数量占总数量的几分之几,再求出各部分的数量。
总份数
各部分的份数
总数量×
=各部分的数量
Text here
深化练习
1. 填一填。
(1)( )∶6=0.75 6∶( )=0.75
4.5
8
(2) ????????=21∶( )=( )÷20=????+?( )????+????????=( ) (填小数)
?
15
28
35
1.4
(3)六年级一班有男生25人,女生20人。男生人数是女生人数的( )倍,女生人数与男生人数的最简单的整数比( ),男生人数占全班总人数的( )。
4∶5
4
5
9
5
(4)两个比的比值是1.5,如果比的前项乘2,后项除以2,这时的比值是( )。
6
(5)甲数的????????等于乙数的????????,甲、乙两数的比是( ),如果甲、乙两数的和是410,则甲数是( ),乙数是( )。
?
20∶21
200
210
Text here
深化练习
2.
选择
(1)一个三角形和一个平行四边形的底相等,面积也相等,它们高的比是( )。
A.1∶2 B.2∶1 C.1∶1
B
(2)一杯混合均匀的糖水中糖与水的比是1∶9,现在喝掉这杯糖水的????????,杯中剩下的糖水中糖与水的比是( )。
A.1∶3 B.1∶9 C.1∶27
?
B
(3)下图中两个图形的周长相等,则a和b的最简单的整数比为( )。
A.5∶4 B.4∶5 C.1∶4
B
用84 cm长的铁丝围成一个长方形,这个长方形的长与宽的比是2 :1。这个长方形的长与宽分别是多少厘米?这块长方形土地的面积是多少平方厘米?
Text here
深化练习
3.
答:这个长方形的长是28厘米,宽是14厘米。面积为392平方厘米。
长
宽
特别注意:周长是2组长与宽的和。
42
长:
宽:
长方形的面积:28×14=392(平方厘米)
Text here
深化练习
一辆汽车从甲地到乙地,第一天行驶了全程的????????,第二天行驶了450km,这时已行驶路程和剩下路程的比是3:7。甲、乙两地间的路程是多少千米?
?
3÷(3+7)=????????????
?
450÷(????????????-????????)=4500 km
?
答:甲、乙两地间的路程是4500 km。
4.
某小学六年级三个班共收集废纸33千克,其中一班收集的比二班多????????,二班收集的比三班少????????????。三个班各收集了多少千克废纸?
?
Text here
拓展练习
5.
1+????????=???????? 一班∶二班=6∶5=12∶10
1 - ????????????=???????????????? 二班∶三班=10∶11
一班∶二班∶三班=12∶10∶11
?
某小学六年级三个班共收集废纸33千克,其中一班收集的比二班多????????,二班收集的比三班少????????????。三个班各收集了多少千克废纸?
?
Text here
拓展练习
5.
33×????????????????+????????+????????=12(千克)
33×????????????????+????????+????????=10(千克)
33×????????????????+????????+????????=11(千克)
答:一班收集了12千克,二班收集了10千克,三班收集了11千克。
人教版·六年级上册
单元知识体系梳理
1
重难点易错点剖析
2
变式巩固练习
3
综合拓展延伸
4
Text here
单元知识体系框架梳理
比
比的各部分名称
比的意义
比的基本性质
比、除法、分数的关系
份数法
化简比
分数法
比的意义
比的基本性质
按比分配问题
Text here
重难易错点剖析
Text here
重难易错点剖析
1.比的意义
比的意义
(1)三好学生占全班人数的 ,三好学生与全班人数的比是( )。
(2)小李5小时加工60个零件,加工个数与时间的比是( ),
4∶5
60∶5
都是人数的比,相比的两个量是同类量。
两个同类量的比表示这两个量之间的倍数关系。
工作总量
工作时间
比
不同类量
两个不同类相关联的量的比表示一个新量。
两个数的比表示两个数相除。
Text here
重难易错点剖析
Text here
重难易错点剖析
2.比的各部分名称
比的意义
前项
后项
比号
比值
……
……
……
……
比值通常用分数表示,能除尽时也可以用小数表示,能整除时就用整数表示。
在两个数的比中,比号前面的数叫做比的前项,比号后面的数叫做比的后项。比的前项除以后项所得的商,叫做比值。例如:
15 : 10也可以写成 ,读作“15比10”
注意:两个数的比表示两个数相除,要注意比的前项和后项的书写顺序,不要颠倒。
Text here
重难易错点剖析
Text here
重难易错点剖析
比的意义
3.比、除法、分数的关系
15 : 10 =
15 ÷ 10 =
除数和分母都不能是0,所以比的后项也不能是0。
????????
?
????????
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
联系
区别
比
除法
分数
分子
—
分母
分数值
一种数
被除数
÷
除数
商
一种运算
前项
:
后项
比值
一种关系
Text here
重难易错点剖析
比的基本性质
4∶5= ( )????????= ????????( )=( )∶15
?
8
35
12
根据比的基本性质,可以把比化成最简单的整数比。
最简单的整数比:前项、后项只有公因数1的整数比。
Text here
重难易错点剖析
比的基本性质
????????∶???????????? ????????∶????????
=(???????? × )∶(???????????? × ) = (????????)(????????) × (????????)(????????)
=( )∶( ) =( )∶( )
?
24
24
9
10
5
9
6
5
2
3
4.化简分数比:
方法一:比的前项、后项同时乘它们分母的最小公倍数 →整数比→最简单的整数比。
方法二:比的前项除以后项,求出比值→化成最简分数→最简单的整数比。
Text here
重难易错点剖析
32∶40
=(32÷8)∶(40÷8)
=4∶5
5.化简整数比。
比的基本性质
比的前项、后项同时除以它们的最大公因数。
最简单整数比
Text here
重难易错点剖析
=(3.2×100)∶(0.16×100)
=(320÷16)∶(16÷16)
=20∶1
比的基本性质
3.2∶0.16
6.化简小数比。
比的前项、后项同时扩大相同的倍数。
整数比
最简单整数比
Text here
重难易错点剖析
按比分配问题
六(1)班分成两组打扫卫生,室外组有30人,室内组有20人,把40个清扫工具按照两个组的人数比分配给各组,室外组、室内组各分到多少个清扫工具?
室外组与室内组的人数比为30:20=3:2
8×3=24(个)
8×2=16(个)
40÷(3+2)=8(个)
答:室外组分到24个清扫工具,室内组分到16个清扫工具。
1.份数法
方法:把比看作分得的份数之比,先求出总份数,然后求出每份的数量,再求出各部分对应的具体数量。
总数量÷总份数=每份的数量
每份的数量×各部分对应的份数=各部分的数量
Text here
重难易错点剖析
按比分配问题
六(1)班分成两组打扫卫生,室外组有30人,室内组有20人,把40个清扫工具按照两个组的人数比分配给各组,室外组、室内组各分到多少个清扫工具?
2.分数法
室外组与室内组的人数比为30:20=3:2
答:室外组分到24个清扫工具,室内组分到16个清扫工具。
=24(个)
3+2
3
40×
40×
3+2
2
=16(个)
方法:把比转化为分数,先求出各部分的数量占总数量的几分之几,再求出各部分的数量。
总份数
各部分的份数
总数量×
=各部分的数量
Text here
深化练习
1. 填一填。
(1)( )∶6=0.75 6∶( )=0.75
4.5
8
(2) ????????=21∶( )=( )÷20=????+?( )????+????????=( ) (填小数)
?
15
28
35
1.4
(3)六年级一班有男生25人,女生20人。男生人数是女生人数的( )倍,女生人数与男生人数的最简单的整数比( ),男生人数占全班总人数的( )。
4∶5
4
5
9
5
(4)两个比的比值是1.5,如果比的前项乘2,后项除以2,这时的比值是( )。
6
(5)甲数的????????等于乙数的????????,甲、乙两数的比是( ),如果甲、乙两数的和是410,则甲数是( ),乙数是( )。
?
20∶21
200
210
Text here
深化练习
2.
选择
(1)一个三角形和一个平行四边形的底相等,面积也相等,它们高的比是( )。
A.1∶2 B.2∶1 C.1∶1
B
(2)一杯混合均匀的糖水中糖与水的比是1∶9,现在喝掉这杯糖水的????????,杯中剩下的糖水中糖与水的比是( )。
A.1∶3 B.1∶9 C.1∶27
?
B
(3)下图中两个图形的周长相等,则a和b的最简单的整数比为( )。
A.5∶4 B.4∶5 C.1∶4
B
用84 cm长的铁丝围成一个长方形,这个长方形的长与宽的比是2 :1。这个长方形的长与宽分别是多少厘米?这块长方形土地的面积是多少平方厘米?
Text here
深化练习
3.
答:这个长方形的长是28厘米,宽是14厘米。面积为392平方厘米。
长
宽
特别注意:周长是2组长与宽的和。
42
长:
宽:
长方形的面积:28×14=392(平方厘米)
Text here
深化练习
一辆汽车从甲地到乙地,第一天行驶了全程的????????,第二天行驶了450km,这时已行驶路程和剩下路程的比是3:7。甲、乙两地间的路程是多少千米?
?
3÷(3+7)=????????????
?
450÷(????????????-????????)=4500 km
?
答:甲、乙两地间的路程是4500 km。
4.
某小学六年级三个班共收集废纸33千克,其中一班收集的比二班多????????,二班收集的比三班少????????????。三个班各收集了多少千克废纸?
?
Text here
拓展练习
5.
1+????????=???????? 一班∶二班=6∶5=12∶10
1 - ????????????=???????????????? 二班∶三班=10∶11
一班∶二班∶三班=12∶10∶11
?
某小学六年级三个班共收集废纸33千克,其中一班收集的比二班多????????,二班收集的比三班少????????????。三个班各收集了多少千克废纸?
?
Text here
拓展练习
5.
33×????????????????+????????+????????=12(千克)
33×????????????????+????????+????????=10(千克)
33×????????????????+????????+????????=11(千克)
答:一班收集了12千克,二班收集了10千克,三班收集了11千克。
