1.1 菱形的性质与判定培优练习2023-2024学年北师大版九年级上册数学(无答案)
文档属性
| 名称 | 1.1 菱形的性质与判定培优练习2023-2024学年北师大版九年级上册数学(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 208.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-06 17:11:33 | ||
图片预览


文档简介
1.1 菱形的性质与判定
一、选择题。
1. 菱形ABCD中,若对角线AC=8cm, BD=6cm,则边长AB等于( )
A.4cm B.5cm C.6cm D.8cm
2. 菱形是轴对称图形,对称轴有( )
A.2条 B.4条 C.6条 D.8条
3.如图,菱形在平面直角坐标系中的位置如图所示,,,则点的坐标为( )
A.
B.
C.
D.
4.如图,在菱形ABCD中,对角线AC与BD相交于点O,AC=8,BD=6,直线OE⊥AD于点E,交BC于点F,则EF的长为( )
A.
5.如图,菱形ABCD的边长为4,E、F分别是AB、AD上的点,连接CE、CF、EF,AC与EF相交于点G,若BE=AF=1,∠BAD=120°,则S△AGF:S△AGE的值为( )
A.1:2 B.1:3 C.1:4 D.1:9
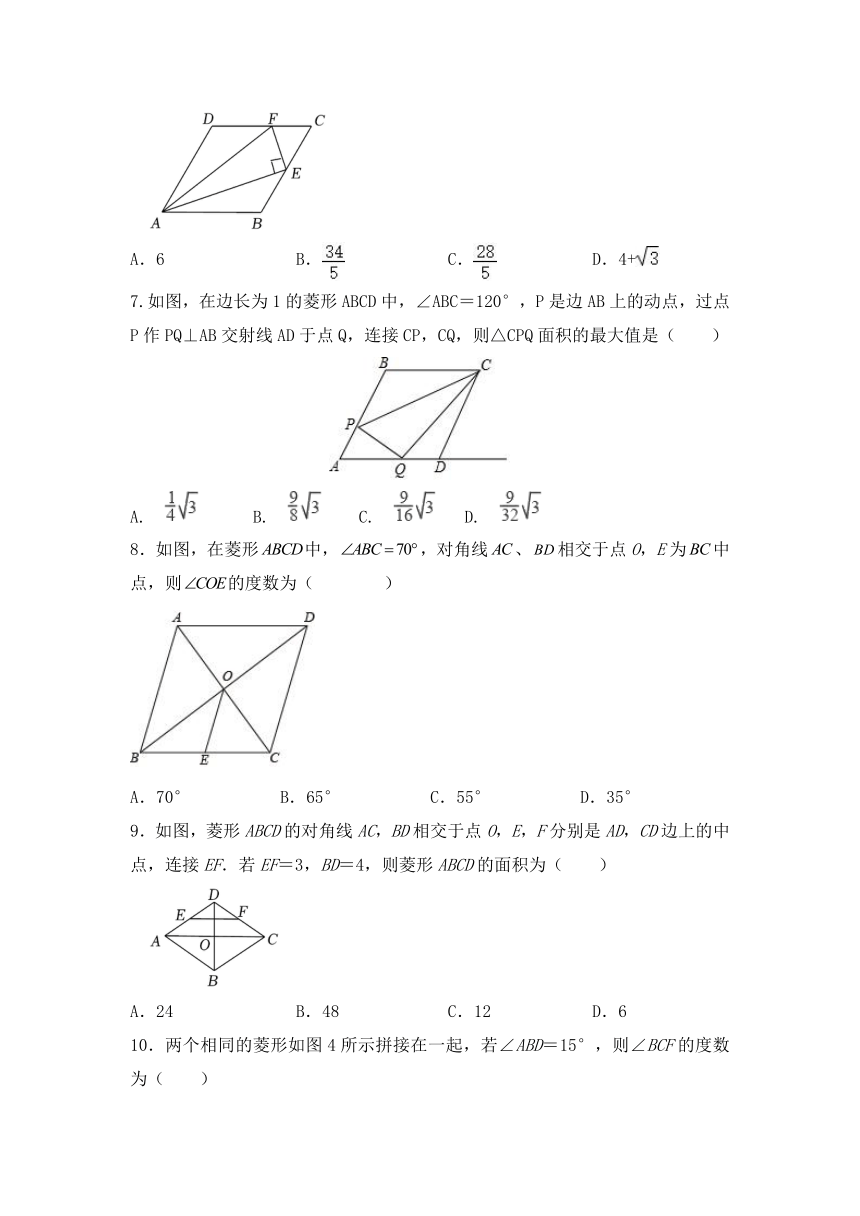
6.如图,在菱形ABCD中,∠C=60°,AB=4,点E为BC的中点,EF⊥AE交CD于点F,连接AF,则线段AF的长为( )
A.6 B. C. D.4+
7.如图,在边长为1的菱形ABCD中,∠ABC=120°,P是边AB上的动点,过点P作PQ⊥AB交射线AD于点Q,连接CP,CQ,则△CPQ面积的最大值是( )
A. B. C. D.
8.如图,在菱形中,,对角线、相交于点O,E为中点,则的度数为( )
A.70° B.65° C.55° D.35°
9.如图,菱形ABCD的对角线AC,BD相交于点O,E,F分别是AD,CD边上的中点,连接EF.若EF=3,BD=4,则菱形ABCD的面积为( )
A.24 B.48 C.12 D.6
10.两个相同的菱形如图4所示拼接在一起,若∠ABD=15°,则∠BCF的度数为( )
A.75° B.60° C.45° D.30°
11.如图,菱形ABCD中,对角线AC,BD交于点O,点E在边BC上,连接AE,OE.若∠CAE=∠OBE,OE=2,CE=,则边AB的长为( )
A. B. C. D.5
12. 如图,在菱形 中,对角线 , 相交于点 ,且 ,则图中全等三角形有
A. 对 B. 对 C. 对 D. 对
二、填空题。
1.如图,在菱形ABCD中,对角线AC、DB相交于点O,且AC≠BD,则图中全等三角形有 对.
2.在菱形ABCD中,,∠A=45°,点E在BC边上,点C'与点C关于直线DE对称,连接DC',若DC'与菱形的一边垂直,则线段CE的长为 .
3.如图,菱形ABCD的对角线AC,BD相交于点O,过点D作DH⊥BC于点H,连接OH,若OA=4,S菱形ABCD=24,则OH的长为 .
4.如图,在菱形ABCD中,∠A=40°,则∠CBD的度数为 .
5. 如图,在菱形ABCD中,对角线AC=6,BD=10,则菱形ABCD的面积为 .
6.如图,在菱形ABCD中,,,垂足分别为点E,F.若,则等于______度.
三、解答题。
1.在①AE=BF;②BE=CF;③∠AED=∠BFD这三个条件中选择一个,补充在下面的问题中,并完成问题的解答.
问题:如图,在菱形ABCD中,∠A=60°,点E、F分别在AB、BC边上,若 ,请判断△DEF的形状,并证明结论.
2.如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若AB=,BD=2,请直接写出△AOE的面积为 .
3. 如图,在 ABCD中,BC=2AB=4,点E、F分别是BC、AD的中点.
(1)求证:△ABE≌△CDF;
(2)当四边形AECF为菱形时,求出该菱形的面积.
4.如图,在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.
(1)证明:四边形ACDE是平行四边形;
(2)若AC=24,BD=10,求△ADE的周长.
5. 如图所示,已知四边形ABCD,ADEF都是菱形,∠BAD=∠FAD,∠BAD为锐角.
(1)求证:AD⊥BF;
(2)若BF=BC,求∠ADC的度数.
6. 已知平行四边形ABCD中,如图,对角线AC和BD相交于点O,AC=10,BD=8.
(1)若AC⊥BD,试求四边形ABCD的面积;
(2)若AC与BD的夹角∠AOD=60°,求四边形ABCD的面积.
一、选择题。
1. 菱形ABCD中,若对角线AC=8cm, BD=6cm,则边长AB等于( )
A.4cm B.5cm C.6cm D.8cm
2. 菱形是轴对称图形,对称轴有( )
A.2条 B.4条 C.6条 D.8条
3.如图,菱形在平面直角坐标系中的位置如图所示,,,则点的坐标为( )
A.
B.
C.
D.
4.如图,在菱形ABCD中,对角线AC与BD相交于点O,AC=8,BD=6,直线OE⊥AD于点E,交BC于点F,则EF的长为( )
A.
5.如图,菱形ABCD的边长为4,E、F分别是AB、AD上的点,连接CE、CF、EF,AC与EF相交于点G,若BE=AF=1,∠BAD=120°,则S△AGF:S△AGE的值为( )
A.1:2 B.1:3 C.1:4 D.1:9
6.如图,在菱形ABCD中,∠C=60°,AB=4,点E为BC的中点,EF⊥AE交CD于点F,连接AF,则线段AF的长为( )
A.6 B. C. D.4+
7.如图,在边长为1的菱形ABCD中,∠ABC=120°,P是边AB上的动点,过点P作PQ⊥AB交射线AD于点Q,连接CP,CQ,则△CPQ面积的最大值是( )
A. B. C. D.
8.如图,在菱形中,,对角线、相交于点O,E为中点,则的度数为( )
A.70° B.65° C.55° D.35°
9.如图,菱形ABCD的对角线AC,BD相交于点O,E,F分别是AD,CD边上的中点,连接EF.若EF=3,BD=4,则菱形ABCD的面积为( )
A.24 B.48 C.12 D.6
10.两个相同的菱形如图4所示拼接在一起,若∠ABD=15°,则∠BCF的度数为( )
A.75° B.60° C.45° D.30°
11.如图,菱形ABCD中,对角线AC,BD交于点O,点E在边BC上,连接AE,OE.若∠CAE=∠OBE,OE=2,CE=,则边AB的长为( )
A. B. C. D.5
12. 如图,在菱形 中,对角线 , 相交于点 ,且 ,则图中全等三角形有
A. 对 B. 对 C. 对 D. 对
二、填空题。
1.如图,在菱形ABCD中,对角线AC、DB相交于点O,且AC≠BD,则图中全等三角形有 对.
2.在菱形ABCD中,,∠A=45°,点E在BC边上,点C'与点C关于直线DE对称,连接DC',若DC'与菱形的一边垂直,则线段CE的长为 .
3.如图,菱形ABCD的对角线AC,BD相交于点O,过点D作DH⊥BC于点H,连接OH,若OA=4,S菱形ABCD=24,则OH的长为 .
4.如图,在菱形ABCD中,∠A=40°,则∠CBD的度数为 .
5. 如图,在菱形ABCD中,对角线AC=6,BD=10,则菱形ABCD的面积为 .
6.如图,在菱形ABCD中,,,垂足分别为点E,F.若,则等于______度.
三、解答题。
1.在①AE=BF;②BE=CF;③∠AED=∠BFD这三个条件中选择一个,补充在下面的问题中,并完成问题的解答.
问题:如图,在菱形ABCD中,∠A=60°,点E、F分别在AB、BC边上,若 ,请判断△DEF的形状,并证明结论.
2.如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若AB=,BD=2,请直接写出△AOE的面积为 .
3. 如图,在 ABCD中,BC=2AB=4,点E、F分别是BC、AD的中点.
(1)求证:△ABE≌△CDF;
(2)当四边形AECF为菱形时,求出该菱形的面积.
4.如图,在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.
(1)证明:四边形ACDE是平行四边形;
(2)若AC=24,BD=10,求△ADE的周长.
5. 如图所示,已知四边形ABCD,ADEF都是菱形,∠BAD=∠FAD,∠BAD为锐角.
(1)求证:AD⊥BF;
(2)若BF=BC,求∠ADC的度数.
6. 已知平行四边形ABCD中,如图,对角线AC和BD相交于点O,AC=10,BD=8.
(1)若AC⊥BD,试求四边形ABCD的面积;
(2)若AC与BD的夹角∠AOD=60°,求四边形ABCD的面积.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
