1.3 正方形的性质与判定培优练习2023—2024学年北师大版数学九年级 上册(无答案)
文档属性
| 名称 | 1.3 正方形的性质与判定培优练习2023—2024学年北师大版数学九年级 上册(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 227.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-06 00:00:00 | ||
图片预览



文档简介
1.3 正方形的性质与判定
一、选择题。
1. 已知四边形 是平行四边形,, 相交于点 ,下列结论错误的是
A. ,
B. 当 时,四边形 是菱形
C. 当 时,四边形 是矩形
D. 当 且 时,四边形 是正方形
2. 在四边形 中,对角线 , 交于点 下列条件中,能判定四边形 为正方形的是
A. ,
B. ,,
C. ,
D. ,,
3.如图,以 的三条边为边,分别向外作正方形,连接 ,,,如果 的面积为 ,则图中阴影部分的面积为
A. B. C. D.
4.如图,在边长为10的正方形ABCD中,点P为对角线AC上一动点,PE⊥AB于E,PF⊥BC于F,则EF的最小值为( )
A. B. C.5 D.
5.如图,四边形ABCD是正方形,G是BC上的任意一点,DE⊥AG于点E,BFDE且交AG于点F,若AB = 4EF,则S正方形ABCD的值为( )
A.9:16 B.17:32 C.17:36 D.18:35
6.如图,正方形 的边长为 ,将正方形折叠,使顶点 落在 边上的点 处,折痕为 .若 ,则线段 的长是
A. B. C. D.
7.如图,将长方形纸片折叠,使A点落在BC上的F处,折痕为BE,若沿EF剪开,则折叠部分是一个正方形,其数学原理是( )
A.邻边相等的矩形是正方形 B.对角线相等的菱形是正方形
C.两个全等的直角三角形构成正方形 D.轴对称图形是正方形
8. 如图,正方形ABCD的顶点A,B分别在x轴,y轴上,A(﹣4,0),G(0,4),BC的中点E恰好落在x轴上,CD交y轴于点F,连接DG,DO.给出判断:①BF=AE;②CD平分∠ODG;③∠AEB+∠CDG=90°; ④△ADO是等腰三角形.其中正确的是( )
A.①②③ B.①②④ C.②③④ D.①③④
9.如图,在四边形ABCD中,点O是对角线的交点,能判定这个四边形是正方形的是( )
A.AC=BD,AB∥CD,AB=CD B.AD∥BC,∠BAD=∠BCD
C.AO=CO,BO=DO,AB=BC D.AO=BO=CO=DO,AC⊥BD
10.定义:我们将顶点的横坐标和纵坐标互为相反数的二次函数称为“互异二次函数”如图,在正方形中,点,点,则互异二次函数与正方形有交点时的最大值和最小值分别是( )
A. ,B. , C. , D. ,
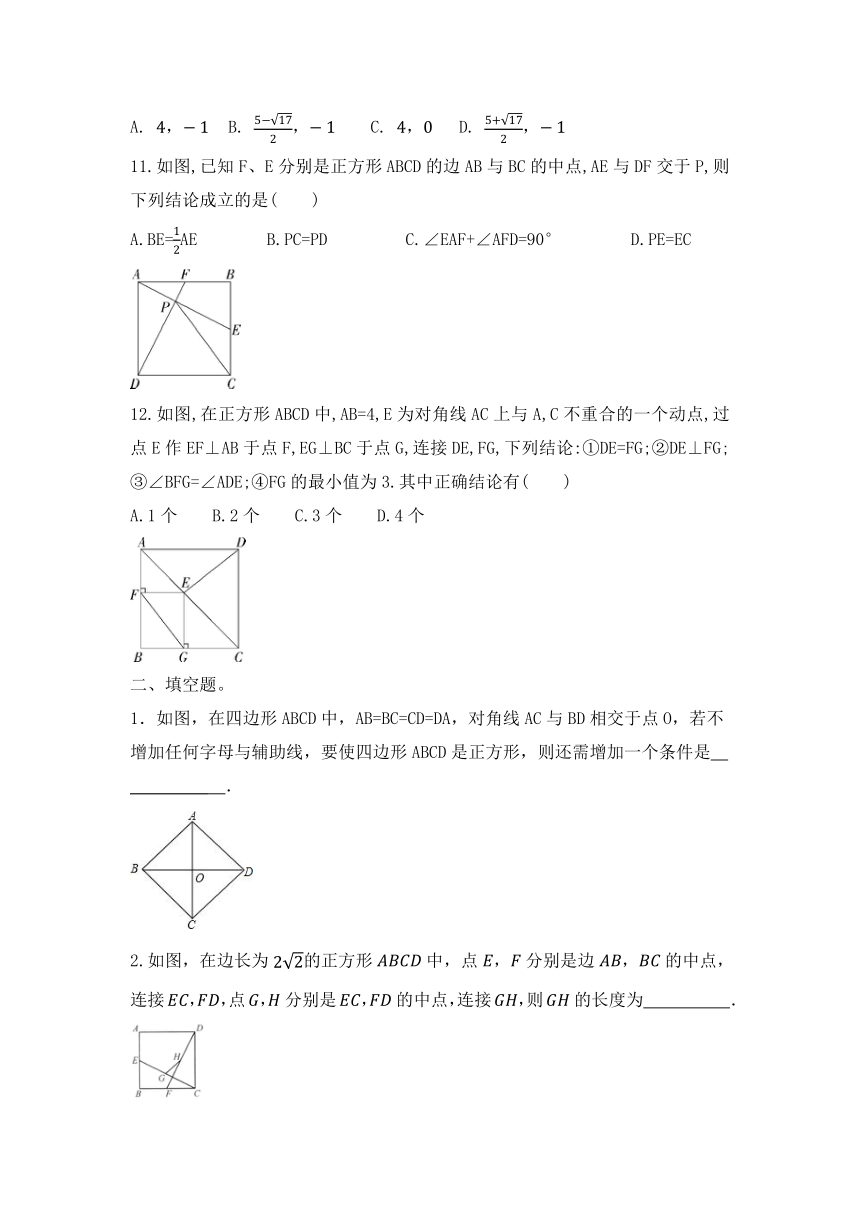
11.如图,已知F、E分别是正方形ABCD的边AB与BC的中点,AE与DF交于P,则下列结论成立的是( )
A.BE=AE B.PC=PD C.∠EAF+∠AFD=90° D.PE=EC
12.如图,在正方形ABCD中,AB=4,E为对角线AC上与A,C不重合的一个动点,过点E作EF⊥AB于点F,EG⊥BC于点G,连接DE,FG,下列结论:①DE=FG;②DE⊥FG;③∠BFG=∠ADE;④FG的最小值为3.其中正确结论有( )
A.1个 B.2个 C.3个 D.4个
二、填空题。
1.如图,在四边形ABCD中,AB=BC=CD=DA,对角线AC与BD相交于点O,若不增加任何字母与辅助线,要使四边形ABCD是正方形,则还需增加一个条件是 _________ .
2.如图,在边长为的正方形中,点,分别是边,的中点,连接,,点,分别是,的中点,连接,则的长度为 .
3.如图,已知正方形 的边长为 ,点 , 分别在 , 上,, 与 相交于点 ,点 为 的中点,连接 ,则 的长为 .
4.如图,为正方形内的一点,绕点按顺时针旋转后成为,连接,若、、三点在同一直线上,则的度数为______.
5.如图,正方形ABCD的边长为2,对角线AC、BD相交于点O,E是OC的中点,连接BE,过点A作AM⊥BE于点M,交BD于点F,则FM的长为 .
6.如图所示,甲、乙、丙、丁四个长方形拼成正方形EFGH,中间阴影为正方形.已知甲、乙、丙、丁四个长方形面积的和是32cm2,四边形ABCD的面积是20cm2,则甲、乙、丙、丁四个长方形周长的总和为 cm.
三、解答题。
1.如图,在正方形 中,点 在 边上,点 在 边上,,.求 的长.
2. 已知:如图,正方形 的对角线 与 相交于点 , 是 上一点,,垂足为点 , 与 相交于点 .
求证:.
3.如图,点E为正方形ABCD外一点,∠AEB=90°,将Rt△ABE绕A点逆时针方向旋转90°得到△ADF,DF的延长线交BE于H点.试判断四边形AFHE的形状,并说明理由.
4.如图,矩形ABCD的对角线AC,BD相交于点O,且DE∥AC,CE∥BD.
(1)求证:四边形OCED是菱形;
(2)若AB=AD,求∠ADE的度数.
5.如图,是正方形对角线上一点,点在上,且.
求证:;
连接,求的度数.
6.如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.
(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.
一、选择题。
1. 已知四边形 是平行四边形,, 相交于点 ,下列结论错误的是
A. ,
B. 当 时,四边形 是菱形
C. 当 时,四边形 是矩形
D. 当 且 时,四边形 是正方形
2. 在四边形 中,对角线 , 交于点 下列条件中,能判定四边形 为正方形的是
A. ,
B. ,,
C. ,
D. ,,
3.如图,以 的三条边为边,分别向外作正方形,连接 ,,,如果 的面积为 ,则图中阴影部分的面积为
A. B. C. D.
4.如图,在边长为10的正方形ABCD中,点P为对角线AC上一动点,PE⊥AB于E,PF⊥BC于F,则EF的最小值为( )
A. B. C.5 D.
5.如图,四边形ABCD是正方形,G是BC上的任意一点,DE⊥AG于点E,BFDE且交AG于点F,若AB = 4EF,则S正方形ABCD的值为( )
A.9:16 B.17:32 C.17:36 D.18:35
6.如图,正方形 的边长为 ,将正方形折叠,使顶点 落在 边上的点 处,折痕为 .若 ,则线段 的长是
A. B. C. D.
7.如图,将长方形纸片折叠,使A点落在BC上的F处,折痕为BE,若沿EF剪开,则折叠部分是一个正方形,其数学原理是( )
A.邻边相等的矩形是正方形 B.对角线相等的菱形是正方形
C.两个全等的直角三角形构成正方形 D.轴对称图形是正方形
8. 如图,正方形ABCD的顶点A,B分别在x轴,y轴上,A(﹣4,0),G(0,4),BC的中点E恰好落在x轴上,CD交y轴于点F,连接DG,DO.给出判断:①BF=AE;②CD平分∠ODG;③∠AEB+∠CDG=90°; ④△ADO是等腰三角形.其中正确的是( )
A.①②③ B.①②④ C.②③④ D.①③④
9.如图,在四边形ABCD中,点O是对角线的交点,能判定这个四边形是正方形的是( )
A.AC=BD,AB∥CD,AB=CD B.AD∥BC,∠BAD=∠BCD
C.AO=CO,BO=DO,AB=BC D.AO=BO=CO=DO,AC⊥BD
10.定义:我们将顶点的横坐标和纵坐标互为相反数的二次函数称为“互异二次函数”如图,在正方形中,点,点,则互异二次函数与正方形有交点时的最大值和最小值分别是( )
A. ,B. , C. , D. ,
11.如图,已知F、E分别是正方形ABCD的边AB与BC的中点,AE与DF交于P,则下列结论成立的是( )
A.BE=AE B.PC=PD C.∠EAF+∠AFD=90° D.PE=EC
12.如图,在正方形ABCD中,AB=4,E为对角线AC上与A,C不重合的一个动点,过点E作EF⊥AB于点F,EG⊥BC于点G,连接DE,FG,下列结论:①DE=FG;②DE⊥FG;③∠BFG=∠ADE;④FG的最小值为3.其中正确结论有( )
A.1个 B.2个 C.3个 D.4个
二、填空题。
1.如图,在四边形ABCD中,AB=BC=CD=DA,对角线AC与BD相交于点O,若不增加任何字母与辅助线,要使四边形ABCD是正方形,则还需增加一个条件是 _________ .
2.如图,在边长为的正方形中,点,分别是边,的中点,连接,,点,分别是,的中点,连接,则的长度为 .
3.如图,已知正方形 的边长为 ,点 , 分别在 , 上,, 与 相交于点 ,点 为 的中点,连接 ,则 的长为 .
4.如图,为正方形内的一点,绕点按顺时针旋转后成为,连接,若、、三点在同一直线上,则的度数为______.
5.如图,正方形ABCD的边长为2,对角线AC、BD相交于点O,E是OC的中点,连接BE,过点A作AM⊥BE于点M,交BD于点F,则FM的长为 .
6.如图所示,甲、乙、丙、丁四个长方形拼成正方形EFGH,中间阴影为正方形.已知甲、乙、丙、丁四个长方形面积的和是32cm2,四边形ABCD的面积是20cm2,则甲、乙、丙、丁四个长方形周长的总和为 cm.
三、解答题。
1.如图,在正方形 中,点 在 边上,点 在 边上,,.求 的长.
2. 已知:如图,正方形 的对角线 与 相交于点 , 是 上一点,,垂足为点 , 与 相交于点 .
求证:.
3.如图,点E为正方形ABCD外一点,∠AEB=90°,将Rt△ABE绕A点逆时针方向旋转90°得到△ADF,DF的延长线交BE于H点.试判断四边形AFHE的形状,并说明理由.
4.如图,矩形ABCD的对角线AC,BD相交于点O,且DE∥AC,CE∥BD.
(1)求证:四边形OCED是菱形;
(2)若AB=AD,求∠ADE的度数.
5.如图,是正方形对角线上一点,点在上,且.
求证:;
连接,求的度数.
6.如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.
(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
